Információk

Főmenü

 Aktuális szám: 27. szám 2023. március 

Bolyai János munkájának hatása a háromdimenziós terek elméletére

Bolyai János munkájának hatása a háromdimenziós terek elméletére

„Semmiből egy ujj más világot teremtettem” írta Bolyai János majd pontosan 200 éve, 1823. november 3-án keltezett levelében édesapjának, Bolyai Farkasnak. János ekkor még nem töltötte be 21. életévét, és a korabeli matematika egyik legfontosabb kérdésére, a párhuzamosok problémájára talált megoldást. Emlékeztetőül: az euklideszi síkon egy rögzített 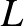$L$ egyenesre egy rajta kívül rögzített 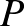$P$ ponton keresztül pontosan egy párhuzamos (vagyis az 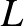$L$ egyenest nem metsző) egyenes húzható. Ez az állítás azonnal következik Eukleidész nevezetes ötödik posztulátumából:

És hogy ha két egyenest úgy metsz egy egyenes, hogy az egyik oldalon keletkező belső szögek (összegben) két derékszögnél kisebbek, akkor a két egyenes végtelenül meghosszabbítva találkozzék azon az oldalon, amerre az (összegben) két derékszögnél kisebb szögek vannak.

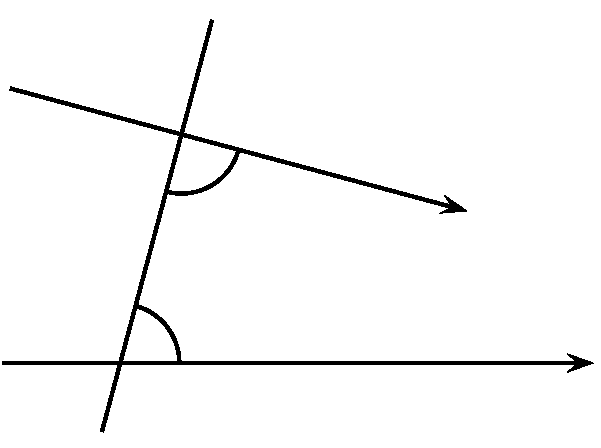
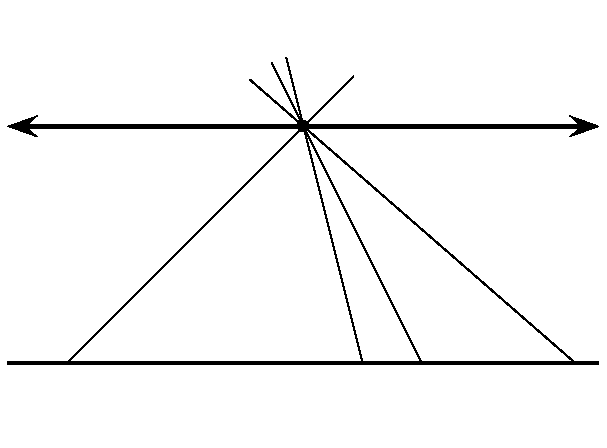
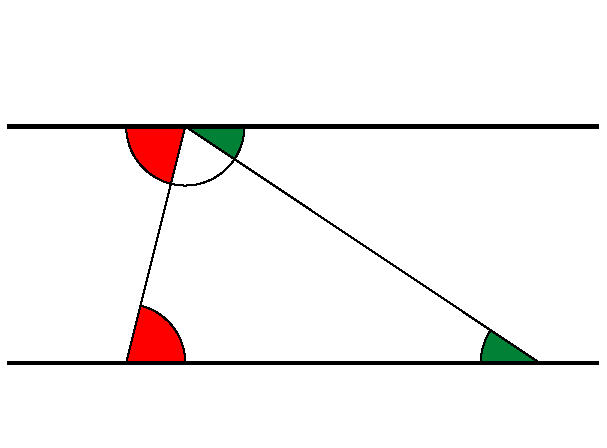
A posztulátum (amit néha axiómának is hívtak) nem véges volta matematikusok számtalan nemzedékét zavarta, és motiválta arra, hogy a többi axióma következményeként mutassák be ezt a tulajdonságot. Számos ekvivalens megfoglamazása is született az idők folyamán, pl. a fenti tulajdonság ekvivalens avval, hogy minden háromszög belső szögeinek összege 180 fokkal egyenlő, vagy avval az állítással, hogy léteznek hasonló, de nem egybevágó háromszögek.

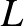Bolyai eredménye lényegében az volt, hogy megmutatta, léteznek más, ugyanannyira koherens geometriai rendszerek, amelyekben a nevezetes 5. Posztulátumon kívül minden euklideszi axióma teljesül, de a fenti $L$ egyeneshez a rajta kívül lévő $P$ ponton át végtelen sok, $L$-et nem metsző (párhuzamos) egyenes húzható.

Mielőtt a Bolyai által talált hiperbolikus sík egy modelljét leírnánk, meg kell említenünk, hogy  nem egyedül Bolyai János jutott erre a gondolatra. Göttingenben Carl Friedrich Gauss (1777–1855), Kazanyban pedig Nyikolaj Ivanovics Lobacsevszkij (1792–1856) találtak hasonló érveket. Gauss ezen eredményeit soha nem jelentette meg, Lobacsevszkij műve pedig 1830-ban született. Bolyai János munkája (egyetlen matematikai témájú publikációja) édesapja Tentamen kötetének függelékeként (mint Appendix) látott napvilágot 1832-ben. Érdekes egybeesésnek gondolhatjuk azt, hogy Európa távoli helyein szinte egyidőben jutott három geométer azonos (vagy legalábbis nagyon hasonló) eredményre. Ugyan a tizenkilencedik század elején-közepén a kommunikáció meglehetősen lassú volt, de Gauss, Bolyai és Lobacsevszkij hasonló hatásoknak voltak kitéve. Amellett, hogy 1760 és 1800 között több mint 60, a párhuzamosság problematikájával foglalkozó mű jelent meg, ismert az is, hogy Bolyai János édesapja, Bolyai Farkas diákként Gauss közeli barátja és diáktársa volt. (Mivel Gauss a későbbiekben semmiféle segítséget nem nyújtott János további munkájának és matematikusi fejlődésének előmozdításához, ez a viszony megromlott.) Gauss általános iskolai mentora, Martin Bartels pedig a Kazanyi Egyetem egyik első professzora lett, és később Lobacsevszkijjel is foglalkozott. (Lobacsevszkij egyébként idővel az egyetem rektora lett.)

     
Bolyai János (1802–1860)    

 

     Nyikolaj Ivanovics Lobacsevszkij (1792–1856)
 

 

    
Bolyai Farkas (1775–1856)   Martin Bartels (1769–1836)   Carl Friedrich Gauss (1777-1855)  

 

Forrás: Wikipedia, MacTutor.

 A hiperbolikus sík több modellje is ismert, alább (csak érintőlegesen) a felső félsík modellt mutatjuk be. Vegyük tehát a szokásos euklideszi felső félsíkot, koordinátákban azon 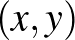$(x,y)$ pontokat, amelyekre 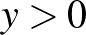$y>0$. Legyenek az egyenesek az 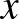$x$ tengelyre merőleges félegyenesek, illetve az 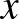$x$ tengelyen levő középponttal rendelkező, felső félsíkba eső félkörök. Nem nehéz látni, hogy ezzel a definícióval az euklideszi axiómák (a nevezetes 5. Posztulátumot leszámítva) teljesülnek, de egy adott egyeneshez egy rajta kívül lévő ponton át végtelen sok párhuzamos húzható. (Ezek közül pedig két kitüntetett található, az elpattanók, amelyek még épp nem metszik az egyenest.)

Egyenesek a hiperbolikus síkon

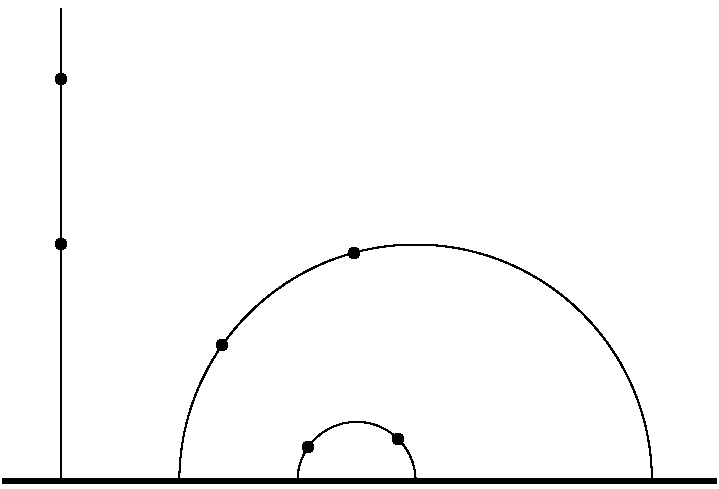
A bal oldali függőleges egyeneshez húzott két párhuzamos

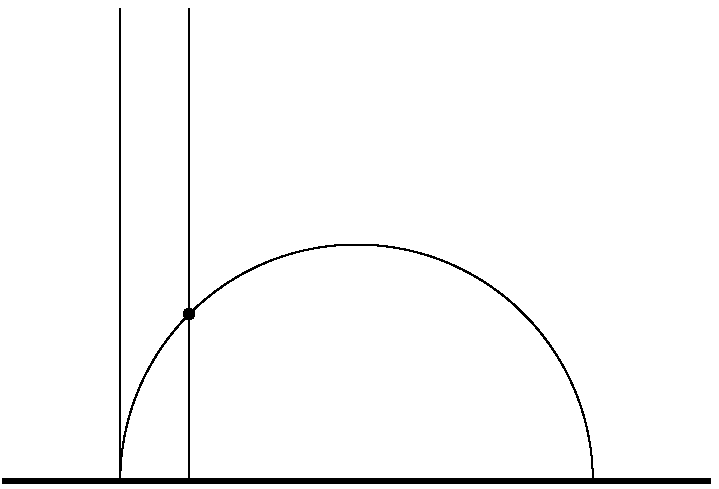
A két elpattanó egyenes (egy-egy kis darabja) és egy párhuzamos

Két egybevágó háromszög

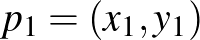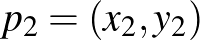Valójában megadható egy távolságmérés a felső félsíkon, amit figyelembe véve, a legrövidebb út két pont között épp a fent leírt egyenesek egyike lesz. A szokásos euklideszi síkon a távolságot a Pitagorasz-tétel alapján kapott formulával határozzuk meg: $p_1=(x_1,y_1)$ és $p_2=(x_2,y_2)$ esetén ez a távolság

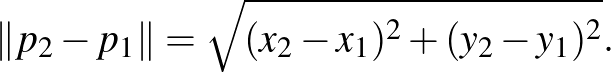
$\displaystyle \Vert p_2-p_1\Vert=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}. $

A hiperbolikus modellben azonban ez a formula a következőre módosul:

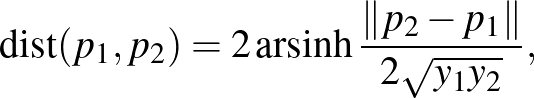
$\displaystyle \operatorname{dist}(p_1,p_2)=2\operatorname{arsinh}\frac{\Vert p_2-p_1\Vert}{2\sqrt{y_1y_2}}, $

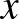ahol $\operatorname{arsinh}$ a $\sinh$ (hiperbolikus szinusz) inverzfüggvénye. Amennyiben a két pont $x$ koordinátái megegyeznek, a képlet a

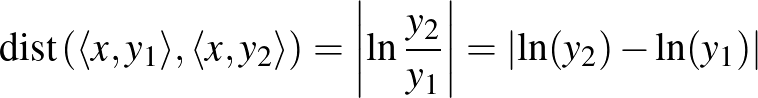
$\displaystyle \operatorname{dist}\left(\langle x,y_1\rangle,\langle x,y_2\rangl... ...left\vert\ln\frac{y_2}{y_1}\right\vert=\left\vert\ln(y_2)-\ln(y_1)\right\vert $

kifejezésre egyszerűsödik. Vagyis a távolság a két 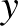$y$ koordináta arányától függ, pl. a (0,0.1) és a (0,1) pontok távolsága éppen akkora, mint a (0,1000) és a (0,10 000) pontok távolsága, bár intuíciónk mást sugallna.

Néhány furcsaság ezen a síkon: egy háromszög belső szögeinek összege 180 foknál kevesebb lesz, és a háromszög területe megegyezik $\pi$ és a szögösszeg különbségével. Ebből kifolyólag, a hiperbolikus síkon nem lehet akármekkora területű egy háromszög, és két háromszög pontosan akkor lesz egybevágó, ha hasonlóak.

Ezek a furcsaságok a művészetet is megihlették, Escher számos képén köszönnek vissza a hiperbolikus sík alapelveit követő motívumok.

circle limit IV

Forrás: https://archive.org/details/EscherMetamorphosisMachine/circle_limit_IV.jpg.

A legfontosabb áttörés ebben a gondolatmenetben az volt, hogy bizony lehet a szokásostól különböző módon távolságot mérni. Ennek teljes elméletét Bernhard Riemann (1826–1866) 1854-es habilitációs előadásában (Gauss témavezetésével) Göttingenben fejtette ki. A végkövetkeztetés az volt, hogy egy téren akkor tudunk geometriáról beszélni, ha megadjuk az érintővektorok hosszát, ekkor pontok távolságát úgy tudjuk megadni, hogy minden sima 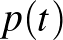$p(t)$ görbére az út = sebesség szorozva idővel  formula (alkalmas integrál alakjával) az

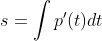
integrált kiszámítva megkapjuk a görbe hosszát, és ezek közül vesszük a legkisebbet (technikai értelemben az infimumot).

Egy ilyen sebesség–hossz rögzítésével ellátott teret ma Riemann-sokaságnak nevezünk, és ezeket vizsgálja a Riemann-geometria. Itt az egyenesek szerepét a geodetikus görbék veszik át (amelyek realizálják két pont közt a legrövidebb utat). Az ilyen Riemann-sokaságok fontos szerepet játszanak nemcsak a matematika különböző ágaiban, de elméleti fizikában is, és alapját adták Einstein általános relativitáselméletének is.

hajlottr

Térjünk vissza azonban a hiperbolikus geometriához. Mint láttuk, ez egy olyan példaként született, amelyben nem teljesül az 5. Posztulátum (de minden további euklideszi axióma igen). Mennyire elterjedt geometria ez?

Vegyük a perem nélküli, véges (szakszóval kompakt), irányítható kétdimenziós felületeket. Ismert eredmény, hogy minden nemnegatív egész számra pontosan egy ilyen alakzat létezik, amennyiben kettőt egyformának tekintünk, ha azok folytonosan, tehát vágás és ragasztás nélkül egymásba alakíthatók. (Ebben az esetben azt mondjuk, hogy a két felület homeomorf.) A felületet jellemző nemnegatív egész számot a felület $g$ nemének (génuszának) nevezzük. Ez a szám azt tükrözi, hogy a felületben hány lyuk van („hány személyes az úszógumi”).

klein

Tétel (Klein, Poincaré, 1882) Egy perem nélküli, kompakt, összefüggő, irányítható felületen pontosan akkor van hiperbolikus geometriát adó metrika, ha $g$ génusza legalább 2.

Röviden tehát, a felületek körében a Bolyai által talált geometria a tipikus, a két kivétel a gömbfelület (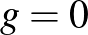$g=0$) és a tórusz (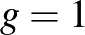$g=1$, vagyis egy fánk felülete), a további végtelen sok eset hiperbolikus struktúrát tud hordozni.

Mi a helyzet a háromdimenziós terekkel? A továbbiakban olyan terekkel foglalkozunk tehát, amik háromdimenziósak (vagyis minden pont kis környezete folytonos értelemben olyan, mint a háromdimenziós terünk, bár a távolságot esetleg máshogy kell rajta mérni). Feltesszük továbbá, hogy terünk perem nélküli, kompakt és irányítható. Mint kiderült, ezen terek osztályozása sokkal bonyolultabb, mint a felületeké, és alapvető tulajdonságaik megismerése továbbra is központi kérdése a matematika „alacsony dimenziós topológia” elnevezésű ágának.

A káoszban William Thurston 70-es években kidolgozott „geometrizációs sejtése” próbált rendet tenni. Eszerint minden háromdimenziós tér gömbök és tóruszok egy jól meghatározott halmaza mentén szétvágható úgy, hogy a részeken nyolc geometria valamelyike megtalálható. (A nyolc geometria között van természetesen a háromdimenziós euklideszi, hiperbolikus és gömbi, de ott van a kétdimenziós gömbi valamint a hiperbolikus szorzata az egydimenziós euklideszivel, és további három furcsább geometria.) Thurston nem tudta belátni ezt a sejtést, de ötlete (hogy geometriát használjunk terek struktúrájának megismerésében) forradalminak bizonyult.

Thurston rajzzal

William Thurston (1946–2012)

Thurston sejtését Grigorij Perelman orosz matematikus látta végül be. 2002. november 11-én tette ki az internetre első, evvel foglalkozó cikkét (majd napra pontosan 200 évvel Bolyai János születése után). Bizonyításának alapja a következő módszer volt: vegyünk egy adott háromdimenziós téren egy tetszőleges metrikát, majd írjunk fel erre egy differenciálegyenletet, ami azt fogja diktálni, hogy a metrika hogyan változik időben. Az általa választott (és Richard Hamilton által már korábban vizsgált) differenciálegyenlet a Ricci-folyam egyenlete:

$\displaystyle \frac{\partial}{\partial t}g(t)=-2\operatorname{Ric}\big(g(t)\big) $

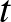Itt $g(t)$ jelöli a Riemann-metrikát (tehát megadja, hogyan mérjük meg egy érintővektor hosszát), amely időben változhat (tehát $g(t)$ a $t$ időpillanatban rögzített metrikát adja meg). 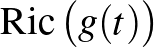$\operatorname{Ric}\big(g(t)\big)$ pedig a $g(t)$ metrika görbületének egy része (az ún. Ricci-tenzor), amelynek pontos leírására nem térünk ki. Azt nézzük tehát, hogy mi történik a metrikával, ha időben úgy változik, ahogy a Ricci-tenzor diktálja.

perelman3

Grigorij Perelman (1966–)

Perelman belátta, hogy ahogyan a folyam előrehalad, a Thurston által jósolt gömbök és tóruszok mentén a metrika degenerálódik. Ezek mentén felvágva, azokon a részeken, ahol a hét nemhiperbolikus metrikát várjuk, a metrika szintén degenerálódik (és ezeket a részeket Perelman más eszközökkel értette meg), a maradékon pedig határértékben (a végtelenben) a metrika hiperbolikus lesz. E tétel egy következménye például, hogy egy tipikus, véletlenszerűen választott háromdimenziós téren hiperbolikus metrika van. Egy szintén korábbi eredmény szerint ez a hiperbolikus metrika pedig lényegében egyértelmű.

Összefoglalásként azt mondhatjuk, hogy az eredetileg a párhuzamossági axiómát nem teljesítő, Bolyaitól származó geometriai konstrukció nemcsak a párhuzamosok problémáját oldotta meg, de megadta a két- és háromdimenziós esetben a „tipikus”, legtöbbször előforduló geometria konstrukcióját is.

Hogy a mi háromdimenziós terünk milyen, azt továbbra sem tudjuk, de meglehetősen jó képünk van a lehetőségekről.

 Stipsicz András
Rényi Alfréd Matematikai Kutatóintézet