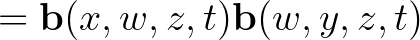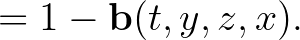Különböző egyenesek négyeseit1 elláthatjuk egy egyértelmű invariánssal, a projektív kettősviszonnyal: két négyes akkor és csak akkor vihető át egymásba valamely lineáris transzformációval, ha megegyezik a kettősviszonyuk. A projektív kettősviszonnyal írható le a projektív egyenes geometriája. Négy egyenes projektív kettősviszonya kiszámolható mint két alkalmas, belőlük alkotott hármas osztóviszonyának hányadosa, innen az elnevezés.
Tekintsünk négy, páronként különböző, az origón áthaladó 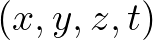 egyenest a síkon. Ekkor léteznek lényegében egyértelmű koordináták, amelyekben
egyenest a síkon. Ekkor léteznek lényegében egyértelmű koordináták, amelyekben 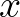 az
az  pontot,
pontot, 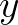 a
a  -et,
-et, 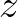 az
az 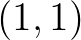 -et, és
-et, és 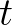 a
a 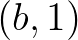 -et tartalmazó, fenti tulajdonságú egyenes, ahol
-et tartalmazó, fenti tulajdonságú egyenes, ahol  a négy egyenes projektív kettősviszonya. A projektív kettősviszony kielégíti függvényegyenletek bizonyos
a négy egyenes projektív kettősviszonya. A projektív kettősviszony kielégíti függvényegyenletek bizonyos 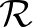 halmazát. Emeljünk ki ezek közül kettőt: az első két változóra vonatkozó multiplikatív kociklus-szabályt és egy additív szabályt:
halmazát. Emeljünk ki ezek közül kettőt: az első két változóra vonatkozó multiplikatív kociklus-szabályt és egy additív szabályt:
Fordítva is igaz: bármely halmaz, ellátva a négyesein egy olyan 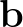 függvénnyel, amely teljesíti
függvénnyel, amely teljesíti 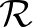 egyenleteit, előállítható a projektív egyenes valamely részhalmazaként úgy, hogy
egyenleteit, előállítható a projektív egyenes valamely részhalmazaként úgy, hogy 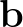 a projektív kettősviszony megszorítása. Ez az elemi, ám figyelemre méltó állítás azt jelenti, hogy a projektív kettősviszony teljesen meghatározza a projektív egyenest. Következésképpen, értelmezhetjük a projektív kettősviszonyt úgy, mint pontnégyeseken értelmezett, bizonyos függvényegyenleteket kielégítő függvényt.
a projektív kettősviszony megszorítása. Ez az elemi, ám figyelemre méltó állítás azt jelenti, hogy a projektív kettősviszony teljesen meghatározza a projektív egyenest. Következésképpen, értelmezhetjük a projektív kettősviszonyt úgy, mint pontnégyeseken értelmezett, bizonyos függvényegyenleteket kielégítő függvényt.
A projektív kettősviszonynak sok leszármazottja létezik az algebrai geometriában: síkok, egyenesek vagy zászlók elrendezéseinek invariánsai. Ezek kifejtését most mellőzzük; ehelyett maradunk a valós és komplex projektív egyenesnél és a kettősviszony negatív görbületű sokaságokkal, hiperbolikus dinamikával és a Teichmüller-elmélettel való kapcsolatánál.
A valós hiperbolikus sík leírható a valós projektív egyenes metrikus kiterjesztéseként. A 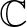 komplex egyenesen (amelyet a komplex projektív egyenes egy affin térképeként tekintünk) a valós egyenesek részhalmaza egy körvonalat alkot2, amely ezáltal bijekcióban áll a valós projektív egyenessel. A Poincaré-féle körlap-modellben a hiperbolikus sík az
komplex egyenesen (amelyet a komplex projektív egyenes egy affin térképeként tekintünk) a valós egyenesek részhalmaza egy körvonalat alkot2, amely ezáltal bijekcióban áll a valós projektív egyenessel. A Poincaré-féle körlap-modellben a hiperbolikus sík az 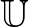 egységkörvonal (mint valós projektív egyenes) által határolt körlap. A hiperbolikus sík geodetikusai az
egységkörvonal (mint valós projektív egyenes) által határolt körlap. A hiperbolikus sík geodetikusai az 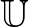 -ra merőleges körvonalak3. Az
-ra merőleges körvonalak3. Az  valós projektív egyenes két tetszőleges pontjára pontosan egy geodetikus illeszkedik. A projektív kettősviszony a következő módon áll kapcsolatban a hiperbolikus távolsággal.
valós projektív egyenes két tetszőleges pontjára pontosan egy geodetikus illeszkedik. A projektív kettősviszony a következő módon áll kapcsolatban a hiperbolikus távolsággal.
 Egy
Egy  -t érintő körvonal a Poincaré-körmodellben az
-t érintő körvonal a Poincaré-körmodellben az  érintési pont mint középpont körül egy horoszféra. Legyen
érintési pont mint középpont körül egy horoszféra. Legyen 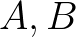 két különböző pont a hiperbolikus síkon, és jelöljük
két különböző pont a hiperbolikus síkon, és jelöljük 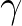 -val a rájuk illeszkedő egyetlen geodetikust. Jelöljük továbbá
-val a rájuk illeszkedő egyetlen geodetikust. Jelöljük továbbá 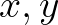 -nal
-nal 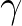 végtelen távoli pontjait4. Legyenek
végtelen távoli pontjait4. Legyenek 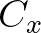 és
és 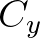 azon horoszférák
azon horoszférák 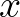 illetve
illetve 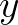 körül, amelyek áthaladnak
körül, amelyek áthaladnak 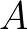 -n illetve
-n illetve 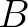 -n. Végül, legyenek
-n. Végül, legyenek 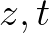 azon
azon 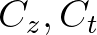 horoszférák középpontjai, amelyek érintik egymást és
horoszférák középpontjai, amelyek érintik egymást és 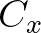 -et illetve
-et illetve 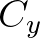 -t. Ekkor,
-t. Ekkor, 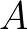 és
és 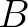 egymástól vett hiperbolikus távolsága az
egymástól vett hiperbolikus távolsága az 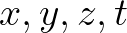 pontok projektív kettősviszonyának logaritmusa. Evvel az eljárással a hiperbolikus távolság és a projektív kettősviszony kölcsönösen meghatározza egymást.
pontok projektív kettősviszonyának logaritmusa. Evvel az eljárással a hiperbolikus távolság és a projektív kettősviszony kölcsönösen meghatározza egymást.
Megfordítva, a valós projektív egyenes a hiperbolikus sík végtelenbeli pereme. A Poincaré-körmodellben két irányított geodetikus akkor és csak akkor végződik azonos 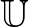 -beli pontban, ha aszimptotikusak egymással, azaz korlátos távolságban maradnak egymástól5. Ez lehetővé teszi a fentiek kiterjesztését Hadamard-felületekre. Egy
-beli pontban, ha aszimptotikusak egymással, azaz korlátos távolságban maradnak egymástól5. Ez lehetővé teszi a fentiek kiterjesztését Hadamard-felületekre. Egy 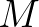 kétdimenziós Riemann-sokaság Hadamard-felület, ha egyszeresen összefüggő, negatív görbületű és teljes.
kétdimenziós Riemann-sokaság Hadamard-felület, ha egyszeresen összefüggő, negatív görbületű és teljes. 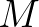 végtelenbeli pereme irányított geodetikusai aszimptotikus ekvivalencia-osztályainak
végtelenbeli pereme irányított geodetikusai aszimptotikus ekvivalencia-osztályainak 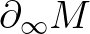 halmaza. A hiperbolikus sík végtelenbeli pereme a valós projektív egyenes. Egy horoszféra egy adott pontot tartalmazó metrikus körvonalak határértéke, amint azok sugara tart a végtelenbe.
halmaza. A hiperbolikus sík végtelenbeli pereme a valós projektív egyenes. Egy horoszféra egy adott pontot tartalmazó metrikus körvonalak határértéke, amint azok sugara tart a végtelenbe.
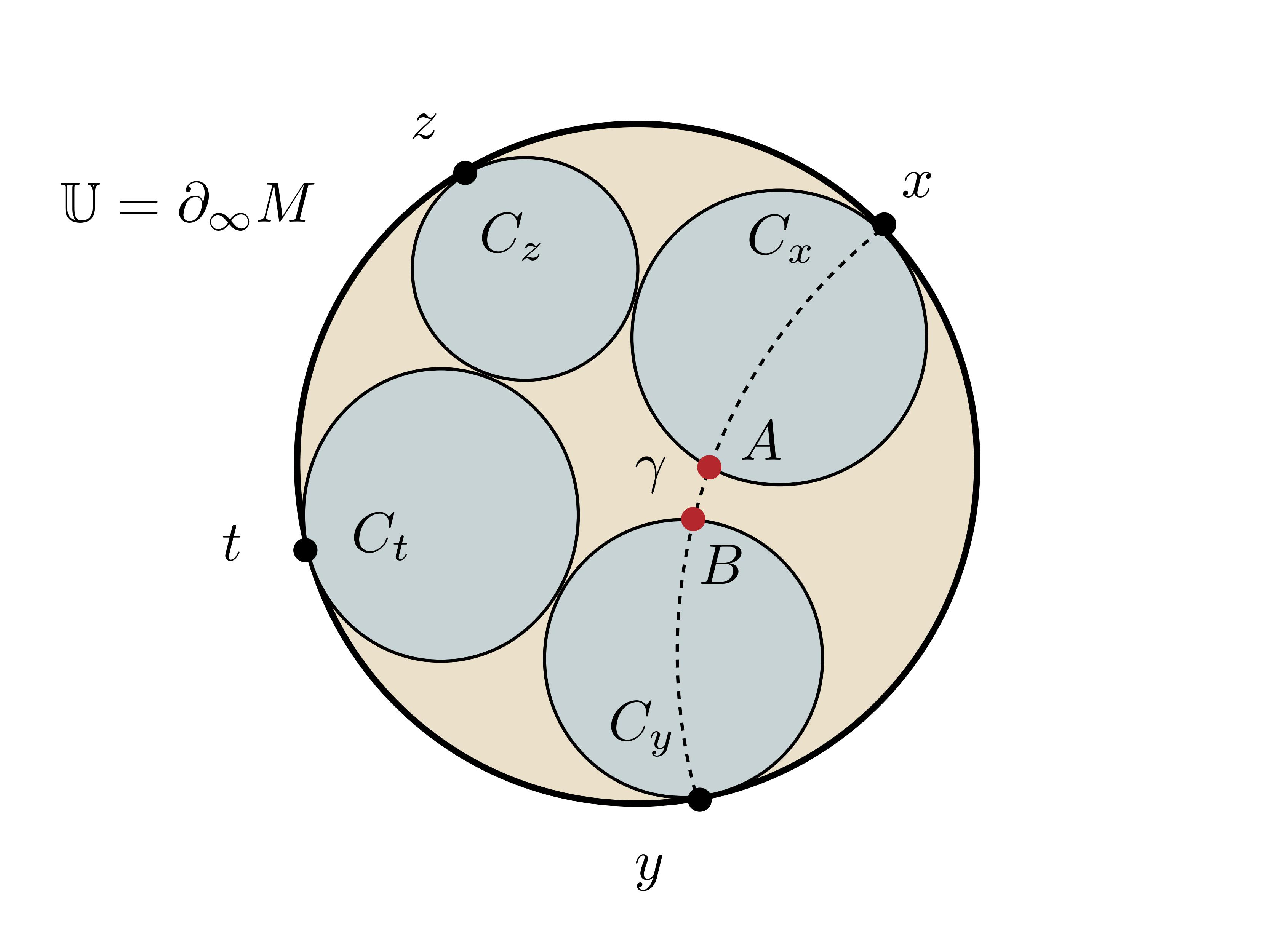
J.-P. Otal a fenti eljárást visszájára fordítva általánosította a kettősviszonyt egy tetszőleges 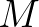 Hadamard-felület
Hadamard-felület 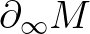 végtelenbeli peremére: négy,
végtelenbeli peremére: négy, 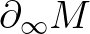 -beli
-beli 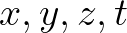 pontból kiindulva tekintsük az ábrán jelölt horoszférákat, és értelmezzük
pontból kiindulva tekintsük az ábrán jelölt horoszférákat, és értelmezzük 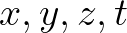 kettősviszonyát úgy, mint az
kettősviszonyát úgy, mint az 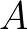 és
és 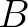 pontok (meghatározott előjellel vett) távolságának exponenciálisát. Általában, az így nyert függvény kielégíti
pontok (meghatározott előjellel vett) távolságának exponenciálisát. Általában, az így nyert függvény kielégíti 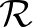 -et, kivéve a (2) additív egyenletet! Értelmezzünk most egy kettősviszonyt egy olyan függvénynek, amely kielégíti ezt a gyengített feltétel-rendszert. Ezt az ötletet felhasználva Otal bebizonyította, hogy egy felületen egy negatív görbületű metrikát határoz meg a zárt geodetikusainak hossza. Bourdon pedig hasonló kettősviszonyok segítségével értelmezett egy durva geometriát egy általános negatív görbületű metrikus tér végtelenbeli peremén.
-et, kivéve a (2) additív egyenletet! Értelmezzünk most egy kettősviszonyt egy olyan függvénynek, amely kielégíti ezt a gyengített feltétel-rendszert. Ezt az ötletet felhasználva Otal bebizonyította, hogy egy felületen egy negatív görbületű metrikát határoz meg a zárt geodetikusainak hossza. Bourdon pedig hasonló kettősviszonyok segítségével értelmezett egy durva geometriát egy általános negatív görbületű metrikus tér végtelenbeli peremén.
Térjünk most át a hiperbolikus dinamikára és Teichmüller-elméletre! Tegyük fel, hogy 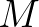 az univerzális fedőfelülete egy
az univerzális fedőfelülete egy 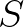 zárt felületnek. Noha
zárt felületnek. Noha 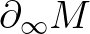 fogalmát
fogalmát 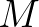 metrikus geometriájából vezettük be, valójában kizárólag a
metrikus geometriájából vezettük be, valójában kizárólag a 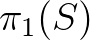 fundamentális csoporttól függ, tehát jelölhetjük a következőképpen is:
fundamentális csoporttól függ, tehát jelölhetjük a következőképpen is: 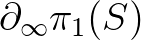 . Ez a végtelenbeli perem homeomorf a körvonallal, és természetes módon hat rajta
. Ez a végtelenbeli perem homeomorf a körvonallal, és természetes módon hat rajta 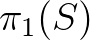 . Tehát, minden negatív görbületű Riemann-metrika
. Tehát, minden negatív görbületű Riemann-metrika 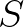 -en meghatároz egy
-en meghatároz egy 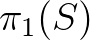 -invariáns kettősviszonyt
-invariáns kettősviszonyt 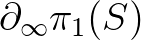 -en.
-en.
Egy kettősviszonynak létezik dinamikai interpretációja is: tekintsük 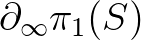 páronként különböző ponthármasainak
páronként különböző ponthármasainak 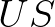 hányadosát a
hányadosát a 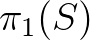 diagonális hatására nézve. Ez a hányados egy kompakt tér. Egy kettősviszony megadja
diagonális hatására nézve. Ez a hányados egy kompakt tér. Egy kettősviszony megadja 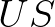 transzformációinak egy
transzformációinak egy 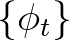 egy-paraméteres részcsoportját a következő szabály szerint:
egy-paraméteres részcsoportját a következő szabály szerint: 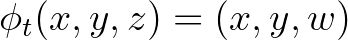 , ahol
, ahol 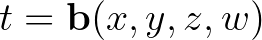 . Ekkor az (1) multiplikatív kociklus-szabály így írható:
. Ekkor az (1) multiplikatív kociklus-szabály így írható: 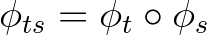 6. Amennyiben a kettősviszony egy negatív görbületű Riemann-metrikából származik, e konstrukció éppen az adott metrika geodetikus áramát adja. Általánosságban, a kettősviszony közeli viszonyban áll a dinamikával.
6. Amennyiben a kettősviszony egy negatív görbületű Riemann-metrikából származik, e konstrukció éppen az adott metrika geodetikus áramát adja. Általánosságban, a kettősviszony közeli viszonyban áll a dinamikával.
Mi a 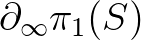 -en értelmezett kettősviszonyok
-en értelmezett kettősviszonyok  tere? Az
tere? Az 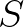 feletti hiperbolikus struktúrákat alkotó Fricke-tér (amelyet Riemann Uniformizációs tétele segítségével gyakran azonosítunk az
feletti hiperbolikus struktúrákat alkotó Fricke-tér (amelyet Riemann Uniformizációs tétele segítségével gyakran azonosítunk az 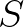 feletti komplex struktúrák
feletti komplex struktúrák 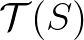 Teichmüller-terével) alkotja
Teichmüller-terével) alkotja  -ben a projektív kettősviszonyok részhalmazát. Minden ilyen kettősviszony azonosítja
-ben a projektív kettősviszonyok részhalmazát. Minden ilyen kettősviszony azonosítja 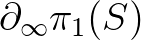 -et a projektív egyenessel, és ezáltal ábrázolja
-et a projektív egyenessel, és ezáltal ábrázolja 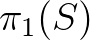 -et
-et 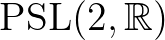 -ben. Hasonlóan, a szerző megmutatta, hogy a
-ben. Hasonlóan, a szerző megmutatta, hogy a 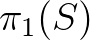 csoport
csoport 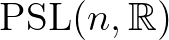 -beli ábrázolásainak egy altere – az úgynevezett Hitchin-komponens – megfelel a (2) bizonyos általánosításait kielégítő kettősviszonyok terének. Végül,
-beli ábrázolásainak egy altere – az úgynevezett Hitchin-komponens – megfelel a (2) bizonyos általánosításait kielégítő kettősviszonyok terének. Végül,  tartalmazza az
tartalmazza az 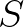 feletti negatív görbületű Riemann-metrikák terét is.
feletti negatív görbületű Riemann-metrikák terét is.
Az  tér feltehetőleg rendelkezik egy érdekes struktúrával, amely általánosítja a Hitchin-komponens Goldman által leírt Poisson-struktúráját. Egy Poisson-struktúra egy
tér feltehetőleg rendelkezik egy érdekes struktúrával, amely általánosítja a Hitchin-komponens Goldman által leírt Poisson-struktúráját. Egy Poisson-struktúra egy 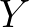 halmazon nem más, mint egy Lie-algebra struktúra az
halmazon nem más, mint egy Lie-algebra struktúra az 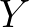 feletti függvények valamely osztályán, amely teljesíti a függvények szorzatára vonatkozó Leibniz-szabályt. E fogalom a klasszikus mechanikából ered, és a kvantummechanikához vezet. Definíció szerint, a végtelenbeli perem minden
feletti függvények valamely osztályán, amely teljesíti a függvények szorzatára vonatkozó Leibniz-szabályt. E fogalom a klasszikus mechanikából ered, és a kvantummechanikához vezet. Definíció szerint, a végtelenbeli perem minden 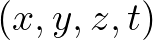 pontnégyese megad
pontnégyese megad  -en egy
-en egy 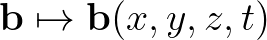 függvényt. E függvények megszorítása a Fricke-térre származtat egy természetes függvényosztályt, amelyen Wolpert és Penner kiszámolta a Poisson-struktúrát. Később Csehov, Fock és Penner kvantálta e függvényeket (azaz: ábrázolta őket egy Hilbert-téren ható operátorokként), egy agyafúrtabb módszerrel pedig Fock és Goncsarov a Hitchin-komponenst kvantálta.
függvényt. E függvények megszorítása a Fricke-térre származtat egy természetes függvényosztályt, amelyen Wolpert és Penner kiszámolta a Poisson-struktúrát. Később Csehov, Fock és Penner kvantálta e függvényeket (azaz: ábrázolta őket egy Hilbert-téren ható operátorokként), egy agyafúrtabb módszerrel pedig Fock és Goncsarov a Hitchin-komponenst kvantálta.
Másrészt, a kettősviszonyok alapvetőek a klasszikus Teichmüller-elmélet több tulajdonságának – úgymint például a McShane-azonosságok – általánosításában egy magasabb Teichmüller-Thurston elméletté, ami a Hitchin-komponens vizsgálatát jelenti.
A komplex projektív kettősviszony továbbá szoros viszonyban áll a háromdimenziós hiperbolikus geometriával. Két friss és szép példa erre W. Neumann tanulmánya Hilbert harmadik problémájának hiperbolikus változatáról, és a Baseilhac, Bonahon, Benedetti, Kashaev, stb. által kidolgozott kvantumhiperbolikus geometria.
A mindenütt jelenlévő kettősviszony által kielégített egyszerű függvényazonosságok elég rugalmasak ahhoz, hogy leírjanak különféle geometriai és dinamikai kérdéseket, azonban elég merevek ahhoz, hogy fontos információt hordozzanak dinamikáról, Poisson-struktúráról és felületek fundamentális csoportjának ábrázolásairól.
François Labourie, “What is...a Cross Ratio?” Notices Amer. Math. Soc. 55 (November 2008), 1234-1235. © 2008 by the American Mathematical Society.
Irodalomjegyzék
- [1] F. Labourie, Cross ratios, surface groups,
 and diffeomorphisms of the circle, Publ. Math. IHES (2007), no. 106, 139-213.
and diffeomorphisms of the circle, Publ. Math. IHES (2007), no. 106, 139-213.
[2] J.-P. Otal, Sur la géométrie symplectique de l'espace des géodésiques d'une variété à courbure négative, Rev. Mat. Iberoamericana (1992), no. 3, 441-456.
[3] W. D. Neumann, Hilbert's 3rd problem and invariants of 3-manifolds, The Epstein Birthday Schrift, 383-411 (electronic), Geom. Top. Monogr., 1, Geom. Topol. Publ., 1998
[4] W. Thurston, Three-Dimensional Geometry and Topology, vol. 1, Princeton University Press (1997).
Lábjegyzetek
- 1négyes alatt végig rendezett négyest értünk (a fordító megjegyzése)
- 2az eredeti szövegben tévesen a következő megfogalmazás szerepel: egy rögzített valós síkot elmetsző komplex egyenesek egy körvonalat alkotnak (a fordító megjegyzése)
- 3beleértve az origón áthaladó egyeneseket is (a fordító megjegyzése)
- 4azaz,
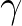 metszéspontjait
metszéspontjait  -val (a fordító megjegyzése)
-val (a fordító megjegyzése) - 5az irányítás szerinti pozitív időtartományra megszorítva (a fordító megjegyzése)
- 6az eredeti szövegben az azonosság bal oldalán
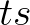 helyett helytelenül
helyett helytelenül 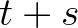 áll, így valójában a
áll, így valójában a 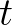 változó logaritmusában kapunk ábrázolást (a fordító megjegyzése)
változó logaritmusában kapunk ábrázolást (a fordító megjegyzése)