A keresés elmélete

Ebben a cikkben röviden összefoglalom a keresés (avagy csoportos tesztelés) nevű matematikai problémakört. Mutatok néhány való életből vett, illetve játékos példát idetartozó problémákra, és felsorolok néhány további kérdést. Végül felidézem azt, amikor néhány évvel ezelőtt a magyar sajtóban már találkozhattunk ezzel a témakörrel, méghozzá nem is csak ismeretterjesztő cikkek formájában, hanem az életünket alapvetően befolyásoló lehetőségként.

1. A barkochba matematikája

Feltételezem, hogy a legtöbb olvasó ismeri a barkochba játékot, de röviden összefoglalom: két játékos játszik, mondjuk András és Barnabás. András gondol valamire (bármire), és Barnabás eldöntendő kérdéseket tesz fel erről a számára ismeretlen dologról vagy személyről. András megválaszolja ezeket, és Barnabás célja kitalálni, hogy András mire gondolt. Általában van egy olyan megkötés is, hogy Barnabás csak egyszer kérdezhet konkrétan rá a megfejtésre, ha például megkérdezi, hogy „Anyukámra gondoltál?” és a válasz nem, akkkor Barnabás veszít. De ez könnyen megkerülhető, ha például azt kérdezi „Valamelyik szülőmre gondoltál?” miközben egy korábbi válaszból kiderült, hogy a megfejtés egy nő.

Nincs a kimondott célok között, hogy minél gyorsabban megtalálja Barnabás a megfejtést, de azért bizonyos értelemben erre szokás törekedni. Mi most azt vizsgáljuk, hogy mennyi a legkevesebb kérdés, amivel Barnabás mindenféleképpen megtalálja a megfejtést (tehát nem számolunk azzal, hogy szerencséje van-e, például hogy elsőnek azt kérdezi, hogy kacsa-e, amikor András Donald kacsára gondolt). Ez azon múlik, hányféle dologra gondolhat András.

Az egyszerűség kedvéért nézzük azt, hogy Barnabás már kitalálta, hogy András valamelyik hónapra gondolt, de semmi többet nem tud. Ekkor 12-féle megfejtés lehet. Egy lehetséges megközelítés, hogy Barnabás először kitalálja, melyik évszakról van szó. Mondjuk végigkérdezi: Tavasz? Nyár? Ősz? Ekkor a telet már nem kell megkérdeznie, három nemleges válasz esetén biztos, hogy egy téli hónapról van szó. Akkor megkérdezi, hogy december-e (illetve valami kerülő kérdés: „Ebben a hónapban van karácsony?”), majd hogy január-e, és kész is vagyunk, hisz két nemleges válasz esetén február a megfejtés. Így öt kérdést tett fel Barnabás. Ennél lehet gyorsabban is: az első kérdéssel kiderítjük, melyik félév, a másodikkal, melyik negyedév, a megmaradó három opcióból pedig egy-egy kérdéssel ki tudunk zárni kettőt, tehát négy kérdés elég.

Azt állítom, hogy ez az optimális. Egy kérdés csak akkor elég, ha összesen két lehetséges megfejtés van, hiszen három vagy több opció esetén valamelyik válaszhoz két megfejtés is tartozik, és kell további kérdés. Két kérdés akkor elég, ha legfeljebb négy opció van, különben valamelyik válasz esetén marad legalább három opció, és ahhoz nem elég a megmaradó egyetlen kérdés. Hasonlóan, három kérdés csak akkor elég, ha legfeljebb nyolc opció van, különben valamelyik válasz után marad legalább öt opció, amihez nem elég a megmaradó két kérdés.

Ez általánosan is igaz: 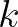$k$ kérdés csak akkor elég, ha legfeljebb 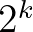$2^k$ lehetséges megfejtés van. Ez belátható 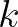$k$ -ra vonatkozó teljes indukcióval: láttuk a 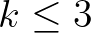$k\le 3$ esetet, általánosan pedig ha több mint 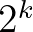$2^k$ lehetséges megfejtés van, akkor valamelyik válasz után marad több mint 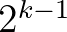$2^{k-1}$ lehetséges megfejtés, amihez az indukciós hipotézis miatt nem elég 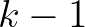$k-1$ kérdés. Hasonlóan lehet belátni, hogy 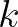$k$ kérdés viszont elég; megint teljes indukciót használunk, és ha legfeljebb 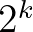$2^k$ lehetséges megfejtés van, akkor olyat kérdez Barnabás, aminél az igen és a nem válasz esetén is legfeljebb 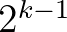$2^{k-1}$ megfejtés marad. Átfogalmazva: ha 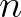$n$ lehetséges megfejtés van, akkor 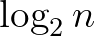$\log_2 n$ kérdés kell és ennyi elegendő is.

Persze a játék szépségét az adja, hogy Barnabásnak nincs listája arról, hogy pontosan mikre gondolhat András. Érdekesség, hogy angolul a játék neve twenty questions, azaz húsz kérdés, mert húsz kérdéssel kell Barnabásnak kitalálnia, amire András gondolt. Ha tehát András legfeljebb 1048576-féle dologra tud gondolni, akkor Barnabás mindig nyerhet (ha elég ügyesen játszik).

Ezt a matematikai problémát teljesen megoldottuk, de hogyan lesz ebből a keresésnek külön elmélete? Ahhoz az kell, hogy az alapprobléma különböző változatait is vizsgáljuk. Ezek egyikét csak némi csalással tudtam kikerülni: amikor azt írtam, hogy 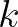$k$ kérdés mindig elég, akkor indoklás nélkül írtam, hogy Barnabás tud olyan kérdést feltenni, aminél az igen és a nem válasz esetén is legfeljebb 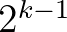$2^{k-1}$ megfejtés marad.

Kimondatlanul arra gondoltam, hogy a lehetséges megfejtések halmazának bármilyen részhalmazát ki tudja választani úgy, hogy azokra jöjjön igen válasz, és tud hozzá egy kérdést kreálni. Például, ha azt akarja megtudni, hogy január, július vagy szeptember-e, akkor megkérdezi: „Ebben a hónapban született valamelyik unokatesóm?” (Persze az is lehet, hogy trükközés nélkül csak megkérdezi, hogy január, július vagy szeptember hónapok egyikére gondolt-e András.) Ez mindenesetre mutat rögtön egy, illetve sok lehetséges variánst: rögzítjük, hogy milyen kérdéseket tehet fel Barnabás.

Erről és más változatokról is beszélünk még, de előbb nézzünk néhány más, az életből vett példát.

2. Rényi autója, cylonok, szifilisz és kémia

Rényi Alfrédnek egyszer elromlott az autója. A szervíz nem állt a helyzet magaslatán, így saját maga akarta megkeresni, hogy melyik alkatrész a hibás. Különböző teszteket végzett, pl. ráadta a gyújtást, beindította a motort, elfordította a kormányt... Ha valamelyik tesztnél rendesen működött a dolog, akkor a hozzá tartózó alkatrészek nem voltak hibásak, ellenkező esetben valamelyikük az volt. Egy teszt tehát megfelelt annak a barkochbakérdésnek: „ezek között az alkatrészek között van-e a hibás?” A témáról sok egyéb érdekességet meg lehet tudni Katona Gyula „Rényi and the Combinatorial Search Problems” című [5] cikkéből.

Christopher Bilder [1] vetette fel, hogy hasonló módszerek segíthetnének a Battlestar Galactica tévésorozat egyik problémájában. Ebben konfliktus van az emberek és a cylonok között. A cylonok teljesen embernek kinéző kémeket építenek be az emberi hadseregbe. Az emberek kidolgoznak egy vértesztet, ami azonosítja a cylonokat, de 61 évig tartana mindenkit letesztelni. Ez a történetszál itt elhal. Pedig fel lehetne gyorsítani a dolgot azzal, hogy több vérmintát egybeöntünk. Ha akár egyetlen cylonnak a vére belekerült a közös mintába, akkor azt kimutatja a teszt. Tehát ha katonák egy 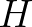$H$ halmazát teszteljük, az eredmény a válasz arra az eldöntendő kérdésre, hogy van-e cylon a 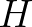$H$ halmazban. Matematikailag ez pontosan ugyanaz, mintha azt kérdeznénk: „a 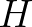$H$ halmaz egyik elemére gondoltál?”. Bilder számítása szerint így akár 101 nap alatt kideríthető, kik a kémek.

Az előbbi persze egy játékos ötlet. De hasonló (teljesen komoly) probléma merült fel az amerikai hadseregben a második világháború idején, csakhogy nem cylon kémeket, hanem szifiliszes betegeket akartak közös teszteléssel megtalálni. Ugyanaz volt az alapötlet, mint amit az előbb leírtam. Dorfman [3] állt elő az ötlettel és a szükséges számításokkal, de végül nem alkalmazták a javaslatait. Valószínűleg azért (és ez az előző példában is gondot okozhatna), mert ha túl sok vérmintát összeöntününk, de csak egyetlen szifiliszes volt a sok minta között, akkor azt már nem mutatja ki a teszt.

Láthatjuk, hogy egy egyszerű játék mellett sok egyéb esetben is használhatunk ilyen módszereket. De ami miatt szerintem érdemes ezt a témakört vizsgálni, az nem a sok különböző probléma, hanem az, hogy ez a megismerés általános modellje. Ha bármi ismeretlennel állunk szemben, és csak részleges információkat tudunk apránként beszerezni, akkor az egy keresési probléma. Ha például van egy folyadékunk, amit azonosítani akarunk, akkor kísérletezünk. Melegítjük, hűtjük, összekeverjük valami más anyaggal, rázzuk, lakmuszpapírt teszünk bele stb. Mindegyik egy teszt, ami a lehetséges folyadékok alaphalmazát szűkíti.

Az eddigi példákban közös volt, hogy egy kérdés vagy teszt egy alaphalmaz valamely részhalmazára vonatkozott, és a válasz az volt, hogy benne van-e egy keresett elem ebben a részhalmazban. Angolul ezt a témakört group testingnek, azaz csoporttesztelésnek is hívják. Elég szerencsétlen elnevezés, mivel a csoport (egy művelettel ellátott halmaz) a modern matematika egyik legfontosabb fogalma, de itt a csoport egyszerűen a köznapi értelemben több elem összessége, azaz egy halmaz, amit egyszerre tesztelünk.

Azonban a felsorolt példák között óriási különbségek is vannak. Míg a barkochbában a szabályok szerint csak egyetlen dologra gondolhat András, az autóban akár több dolog is tönkremehet. A folyadék egyféle folyadék. A cylonok valószínűleg egynél több, de nem sok kémet küldenek, szifiliszes viszont biztos, hogy rengeteg volt a seregben. További fontos dolog, hogy az autóban minden hibás részt meg akarunk találni, különben semmit sem ér a tesztelés. A cylonok közül is mindet meg akarjuk találni, de ha csak néhányat találunk, az is már siker. A szifiliszeseknél viszont az volt a lényeg, hogy a zömüket megtalálják, néhány beteg a hadseregben nem olyan veszélyes, mint néhány kém.

3. Változatok

Vizsgáljuk meg az alapprobléma néhány változatát! A célom az, hogy egy kis ízelítőt adjak a problémák tárházából. Ebből ki fog derülni, miért beszélhetünk önálló témakörként a keresésről.

Már említettem azt az esetet, amikor nem minden kérdés megengedett. Adott egy 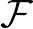$\mathcal{F}$ halmazrendszer, és csak olyat kérdezhetünk, hogy ha veszünk egy 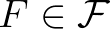$F\in \mathcal{F}$ halmazt, a keresett elem benne van-e 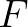$F$ -ben? Ide tartozik a talán legtöbbet vizsgált keresési probléma, a sorbarendezés. Adott 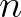$n$ különböző szám és nagyság szerint növekvő sorrendbe akarjuk rakni őket páronkénti összehasonlításokkal. Itt az alaphalmaz az 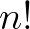$n!$ -féle lehetséges sorrend, ezek egyikét (a tényleges sorrendet) akarjuk megtalálni. Egy összehasonlítás az egy kérdés: 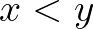$x<y$ ? Jelölje 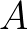$A$ azon sorrendeket, ahol 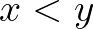$x<y$ . Ekkor ez a kérdés úgy is megfogalmazható: a keresett sorrend 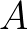$A$ -ban van?

Már említettem azt is, hogy több dolgot, például több beteget is kereshetünk egyszerre. Ilyenkor egy kérdés így hangzik: „Van-e 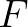$F$ -ben legalább egy beteg?” Vagy további változat lehet, hogy másféle kérdéseket használunk, például van-e 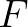$F$ -ben legalább 10 beteg?” De azt is tisztáznunk kell, összesen mit tudunk, hány beteg van. Lehet azt vizsgálni, hogy pontosan 100, legalább 100, legfeljebb 100 van-e, de itt át is térhetünk egy másik variánsra: a véletlen használatára.

Valójában az egész témakörnek két nagy és elkülönülő ága van: a kombinatorikus keresés és a véletlenes keresés. Eddig csak a kombinatorikus keresésről beszéltem, részben azért, mert ez jobban érthető magasabb matematikai ismeretek nélkül, de főleg azért, mert én ehhez értek. Gondoljunk vissza a szifiliszes példára, és nézzük meg, hogy mi a lehetséges, és mi a fontos gyakorlati szempontból. Azt nem tudjuk, hogy konkrétan hány beteg van. Ehelyett valami előzetes elképzelésünk van arról, hogy milyen lehet a betegek számának eloszlása. Persze emiatt nem fogjuk tudni pontosan megmondani, hogy hány kérdésre lesz szükség, de ez nem is fontos. Inkább úgy akarjuk megtervezni a kérdéssorozatot, hogy átlagosan kevés kérdésre legyen szükség.

Egy újabb variáns, amit az eddigi példák indokolnak, amikor nem csak kétféle válasz lehet. Már a barkochba során is szokás is-is választ adni, egy autónal is van átmenet aközött, hogy működik-e vagy sem, egy kémiai kísérletnél pedig lehet, hogy a folyadék zöld lesz vagy kék vagy lila vagy bármi más színű.

Eddig úgy kezeltük, hogy csak a kérdések száma számít, az nem, hogy milyen kérdést teszünk fel. Pedig nyilván egyszerűbb egy vérmintát tesztelni, mint összeönteni tizet és azt tesztelni (pláne ha van millió vérmintánk, és ki kell keresni közülük azt a tizet, amit összeöntünk). Egy kémiai kísérletnél is lehet, hogy valamilyen teszthez drága anyagok, eszközök kellenek.

Mindeddig feltételeztük, hogy a tesztek eredménye mindig pontos. A barkochbában is előfordulhat, hogy a válaszoló rosszul tud valamit, vagy lehet egy félreértés is. Az persze világos, hogy egyetlen rossz válasz is eléggé félrevihet, és Barnabás hosszasan találgathatja, melyik mesehősre gondolt András, mielőtt kiderül, hogy rosszul hallotta és nem kitalált személyről van szó. Lehet vizsgálni, hogy mi van, ha összesen 10-szer tévedhet András, vagy ha öt kérdésenként egyszer. A gyakorlati alkalmazásoknál tipikusan inkább azt érdemes feltételezni, hogy minden válasz hibás valamekkora eséllyel. Vérminták tesztelésénél és kémiai kísérleteknél ezt az esélyt jól meg lehet becsülni.

A barkochbának úgy van értelme, ha minden válasz után töprenghet egy kicsit Barnabás, hogy kitalálja a következő kérdést. A vérmintákat viszont lehet egyszerre is tesztelni. A nem adaptív változatban az összes kérdést egyszerre tesszük fel. Átmeneti változat, hogy adott számú forduló alatt kell feltenni a kérdéseket, és a fordulók végén egyszerre kapjuk meg a válaszokat a forduló kérdéseire, és ezek alapján kell kitalálnunk a következő forduló kérdéseit. Érdekesség, hogy ha mindenféle kérdést megengedünk, akkor ez egyáltalán nem lassít le minket, 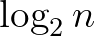$\log_2 n$ kérdés továbbra is elég. Tegyük fel, hogy 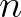$n$ lehetséges megfejtés van, rakjuk őket sorba tetszőlegesen. Legyenek a kérdések a következők: „Ha a megfejtés a sorrendben az 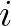$i$ -edik, akkor 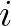$i$ kettes számrendszerbeli alakjának a 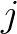$j$ -edik számjegye 1?”. Ha 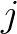$j$ = 1, 2, ... 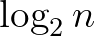$\log_2 n$ , akkor az 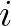$i$ kettes számrendszerbeli alakjának összes számjegyét megtudjuk, tehát megtudjuk 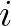$i$ -t, vagyis a megfejtést is.

Ezeket a változatokat és még sok mást is, illetve ezek kombinációját is mind vizsgálják. Így lesz egyetlen könnyen megoldható kérdésből egy óriási témakör.

4. Covid

Nem is olyan régen a magyar olvasók már találkozhattak a csoportos teszteléssel a sajtóban. A koronavírus kapcsán is felvetődött ugyanis, hogy ezzel lehetne felgyorsítani a tesztelést, pontosabban elérni azt, hogy mindenkit tesztelni tudjunk belátható idő alatt. Glattfelder Tamás közgazdász és Török Ákos informatikus a meglévő matematikai kutatások ismerete nélkül jutott erre az ötletre. Egy nyilvános fórumon vitatták meg, és rengeteg különféle szakember csatlakozott hozzájuk, hogy kisebb-nagyobb mértékben segítsen megoldani a felmerülő biológiai, informatikai, szervezési, technológiai és egyéb problémákat. Közérthető összefoglalókat találunk itt: [10] és [11]. További részleteket találunk itt: [9], és a teljes nyilvános kommunikációt itt: [7].

A matematikai részt főként Csóka Endre vállalta magára. A felmerülő problémákról egy matematikai cikket is írt [2]. Az következő példa jó arra, hogy a valóságban mennyi probléma felmerülhet, ami a matematikusoknak eszükbe se jut: említettük az adaptív, többkörös és nemadaptív változatot. Kiderült, hogy itt ezek egyikének sincs értelme, folyamatosan érkeznek a minták, és folyamatosan kell az eredményeknek is jönniük, hiszen senki se várhat hetekig a teszteredményére. Az első tesztben szereplő minták következő kérdésével nemhogy nem várhatjuk meg az ezredik teszt eredményét, de azt se várhatjuk meg, hogy beérkezzenek azok a minták, amik az ezredik tesztben szerepelnek.

Másoknak is eszébe jutott ez az ötlet, hogy COVID-19 teszteléssel kapcsolatosan vizsgálják a csoportos tesztelést. Egy 2022-es cikk [4] 20 olyan szakcikket idéz, ami ennek a matematikáját vizsgálja. Ez persze csak a probléma kisebb része, egy 2020-as cikket, ami a COVID csoporttesztelés biológiai részével foglalkozik, már 297 másik cikk idéz.

Magyarországon az állam úgy döntött, hogy csak azokat kell tesztelni, akik kontaktjaik vagy tüneteik miatt fertőzésgyanúsak, de több más országban volt tömeges tesztelés, akár milliókat is teszteltek rövid időn belül. Ezzel együtt nem tudok olyan esetről, amikor ténylegesen csoporttesztelést alkalmaztak volna sok embernél (csak olyat, ahol tesztelték, hogy jól működik-e a csoporttesztelés).

Végül kötelességem megemlíteni a matematikai eszköztár határait is. Egy kommentemet idézem [8], ahol azzal számoltam, hogy 16 embert lehet egyszerre tesztelni, és az egyszerűség kedvéért tízmillió magyar van és körülbelül 0,1%-uk fertőzött. A legegyszerűbb algoritmus, ami matematikai ismeretek nélkül is sokaknak eszébe jut, hogy teszteljük 16-osával az embereket, és ha a teszt azt mutatja, hogy van köztük fertőzött, akkor mind a 16-ot egyenként leteszteljük. Ekkor a tízmillió teszt helyett biztosan elég valamivel kevesebb mint nyolcszázezer. Az viszont biztos, hogy az első csoportos tesztelésen mindenkiinek részt kellene vennie, ezért kell legalább 625000 teszt. Minden további matematikai gondolkodás azért kell, hogy ehhez minél közelebb tudjunk kerülni. Tehát az alapötlet több mint 90 százalékkal csökkenti a tesztek számát a tesztelendők számához képest, és minden egyéb ötlet próbál még 2 százalékpontot spórolni.

Irodalomjegyzék

: [1] C. R. Bilder. Human or Cylon? Group testing on ‚Battlestar Galactica’. Chance, 22(3), 46–50, 2009.

[2] E. Csóka. Application-oriented mathematical algorithms for group testing. arXiv preprint arXiv:2005.02388, 2020.

[3] R. Dorfman. The detection of defective members of large populations. The Annals of Mathematical Statistics, 14(4), 436–440, 1943.

[4] D. Hong, R. Dey, X. Lin, X. B. Cleary, E. Dobridan. Group testing via hypergraph factorization applied to COVID-19. Nat. Commun. 13(1), 1–13, 2022.

[5] G.O.H. Katona. Rényi and the Combinatorial Search Problems. Studia Sci. Math. Hungar., 26, 363–378, 1991.

[6] S. Lohse, T. Pfuhl, B. Berkó-Göttel, J. Rissland, T. Geißler, B. Gärtner, S.L. Becker, S. Schneitler, S. Smola. Pooling of samples for testing for SARS-CoV-2 in asymptomatic people. The Lancet Infectious Diseases 20(11), 1231–1232, 2020.

[7] https://groups.google.com/g/suppress-covid19-pandemic

[8] https://groups.google.com/g/suppress-covid19-pandemic/c/QkzuIe-GjJE/m/ef7RY-7dBwAJ

[9] https://sites.google.com/a/torokcsalad.hu/poroly/home

[10] https://qubit.hu/2020/03/31/egy-pofonegyszeru-es-olcso-rutinmegoldassal-napok-alatt-le-lehetne-tesztelni-a-teljes-magyar-nepesseget

[11] https://qubit.hu/2020/04/09/ed-kiterjedt-tesztelessel-emberi-eleteket-es-a-gazdasagot-is-meg-lehetne-menteni

Gerbner Dániel

Rényi Alfréd Matematikai Kutatóintézet

(A főoldalon Gerd Altman képe a Pixabay-ről.)