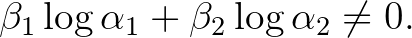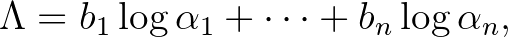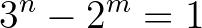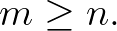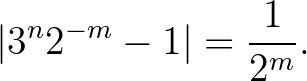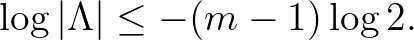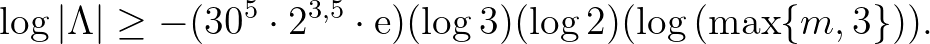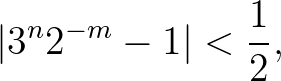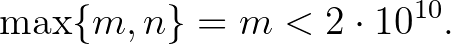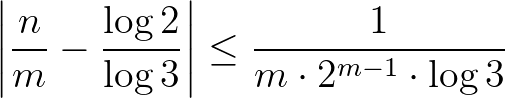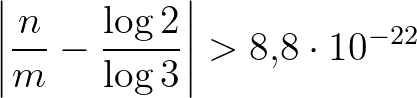Ezen cikk célja, hogy rövid betekintést nyújtson a diofantikus számelmélettel foglalkozó kutatók által sokszor idézett és alkalmazott, Alan Baker Fields-érmes matematikus nevével fémjelzett, ún. Baker-módszerbe.
Ehhez először néhány alapvető definíciót ismertetünk. Az 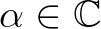 komplex számot algebrai számnak nevezzük, ha
komplex számot algebrai számnak nevezzük, ha 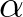 gyöke egy nem azonosan nulla egész együtthatós polinomnak. Megmutatható, hogy minden
gyöke egy nem azonosan nulla egész együtthatós polinomnak. Megmutatható, hogy minden  algebrai szám esetén létezik egyetlen olyan minimális fokszámú
algebrai szám esetén létezik egyetlen olyan minimális fokszámú 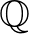 felett irreducibilis
felett irreducibilis ![$m_{\alpha}(x)=a_0x^k+a_1x^{k-1}+\ldots+a_k \in \mathbb{Z}[x]$](/images/stories/latexuj/2022-02/2022-02-abakermodszeresegyalkalmazasa/img4.png) egész együtthatós polinom, amelyre
egész együtthatós polinom, amelyre 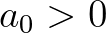 ,
, 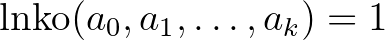 és amelynek
és amelynek  gyöke. Ezt a polinomot az
gyöke. Ezt a polinomot az  definiáló polinomjának, ezen polinom fokszámát pedig
definiáló polinomjának, ezen polinom fokszámát pedig  fokának nevezzük. Ha az
fokának nevezzük. Ha az 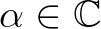 szám nem algebrai, akkor transzcendensnek hívjuk.
szám nem algebrai, akkor transzcendensnek hívjuk.
1844-ben Liouville [19] konstruált először explicit módon transzcendens számokat. Megmutatta, hogy pl. a 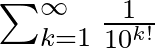 szám transzcendens. Megjegyezzük, hogy míg transzcendes számokat konstruálni viszonylag egyszerű, addig jóval nehezebb feladat megmutatni egy adott komplex számról, hogy transzcendens-e vagy sem. Ebben a tekintetben megemlítjük, hogy Hermite 1873-ban igazolta, hogy az
szám transzcendens. Megjegyezzük, hogy míg transzcendes számokat konstruálni viszonylag egyszerű, addig jóval nehezebb feladat megmutatni egy adott komplex számról, hogy transzcendens-e vagy sem. Ebben a tekintetben megemlítjük, hogy Hermite 1873-ban igazolta, hogy az 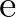 szám transczcendens, míg Lindemann 1882-ben bizonyította a
szám transczcendens, míg Lindemann 1882-ben bizonyította a 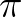 transzcendenciáját.
transzcendenciáját.
1900-ban a Párizsban megrendezett II. Nemzetközi Matematikai Kongresszuson David Hilbert, a világ ekkor már elismerten egyik legnagyobb matematikusa, „Matematikai problémák” címmel tartott, később óriási jelentőségre szert tevő előadást, amiben felsorolta a matematika szerinte legfontosabb problémáit. Ebből a hetedik probléma bizonyos alakú számok transzcendenciájára vonatkozik.
1. probléma. (Hilbert 7. problémája) Ha 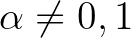 algebrai szám és
algebrai szám és 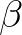 irracionális algebrai szám, akkor
irracionális algebrai szám, akkor 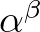 transzcendens.
transzcendens.
A fenti problémát Hilbert nagyon nehéznek érezte és ezzel kapcsolatban az alábbi megjegyzéseket tette:
„A 7. probléma nagyon nehéz, így érdemes összehasonlítani néhány ismert problémával.
A Riemann-hipotézis bizonyítása irányába az utóbbi években komoly előrehaladás történt, így nagyon remélem, hogy még megérem a bizonyítását.
Számos biztató eredmény van a Fermat-sejtéssel kapcsolatban is, ezért talán a hallgatóság legfiatalabb tagjai megérik a sejtés bizonyítását.
Annak a bizonyítását azonban, hogy a 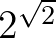 transzcendens szám, a jelenlevők közül senki sem fogja látni.”
transzcendens szám, a jelenlevők közül senki sem fogja látni.”
Ma már tudjuk, hogy Gelfond és Schneider alább ismertetendő tételének köszönhetően (ld. 1. tétel), Hilbert 7. problémája megoldottnak tekinthető, valamint Wiles [27] munkájának köszönhetően a Fermat-sejtést is sikerült igazolni. A Hilbert által „legkönnyebbnek” gondolt probléma, azaz a Riemann-sejtés, még mindig megoldatlan.
Gelfond és Schneider tételének ismertetéséhez szükségünk lesz egy nemnulla komplex szám logaritmusának a főértékére1. Mint ismert, minden 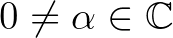 felírható
felírható  alakban, ahol
alakban, ahol 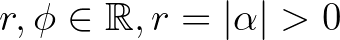 . Ekkor
. Ekkor  alatt a logaritmus főértékét értjük, azaz
alatt a logaritmus főértékét értjük, azaz 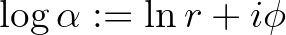 , ahol
, ahol 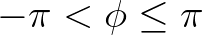 .
.
Hilbert 7. problémáját Gelfond és Schneider egymástól függetlenül igazolta (ld. [13] és [23]).
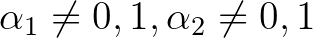 valamint
valamint 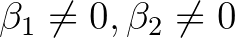 olyan tetszőleges algebrai számok, amelyekre
olyan tetszőleges algebrai számok, amelyekre 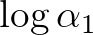 és
és 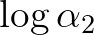 lineárisan függetlenek a racionális számtest fölött2. Ekkor
lineárisan függetlenek a racionális számtest fölött2. Ekkor
Megmutatható, hogy az 1. tétel implikálja Hilbert 7. problémáját, így végtelen sok példát szolgáltat transzcendens számokra. Ezért pl. a Hilbert által felvetett 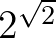 szám transzcendens. Továbbá, mivel a jól ismert Euler-formula miatt
szám transzcendens. Továbbá, mivel a jól ismert Euler-formula miatt 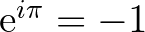 , ezért Hilbert 7. problémáját felhasználva adódik, hogy az
, ezért Hilbert 7. problémáját felhasználva adódik, hogy az 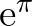 szám is transzcendens, hiszen
szám is transzcendens, hiszen
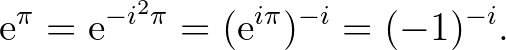
A Gelfond és Schneider által egymástól függetlenül igazolt 1. tétel az 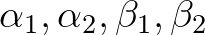 algebrai számokra tett bizonyos feltételek mellett azt állítja, hogy az (1) kétváltozós logaritmikus lineáris forma nem lehet nulla. Természetes módón merül fel tehát a kérdés, hogy ekkor a
algebrai számokra tett bizonyos feltételek mellett azt állítja, hogy az (1) kétváltozós logaritmikus lineáris forma nem lehet nulla. Természetes módón merül fel tehát a kérdés, hogy ekkor a  mennyiség mennyire lehet közel nullához. Ebben a tekintetben megemlítjük Gelfond egy 1935-ben közölt eredményét (ld. [14]).
mennyiség mennyire lehet közel nullához. Ebben a tekintetben megemlítjük Gelfond egy 1935-ben közölt eredményét (ld. [14]).
2. tétel. (Gelfond (1935)) Legyenek 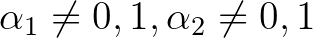 olyan tetszőleges algebrai számok, amelyekre
olyan tetszőleges algebrai számok, amelyekre 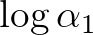 és
és 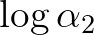 lineárisan függetlenek a racionális számtest fölött és tegyük fel, hogy
lineárisan függetlenek a racionális számtest fölött és tegyük fel, hogy 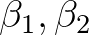 olyan tetszőleges egészek, amelyek közül legalább az egyik nemnulla. Ekkor bármely
olyan tetszőleges egészek, amelyek közül legalább az egyik nemnulla. Ekkor bármely 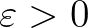 esetén létezik egy
esetén létezik egy 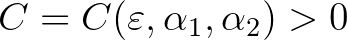 effektíve meghatározható konstans3 úgy, hogy
effektíve meghatározható konstans3 úgy, hogy
ahol 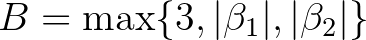 .
.
Gelfond megjegyezte, hogy az 1. tétel valamint a 2. tételben szereplő (2) becslés megfelelő kiterjesztése tetszőleges 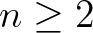 változós logaritmikus lineáris formákra jelentős eredményekre vezetne a diofantikus approximáció valamint a diofantikus egyenletek elméletében. Az áttörést, valamint Gelfond és Schneider 1. tételének, illetve Gelfond 2. tételének messzemenő kiterjesztéseit Alan Baker 1960-as évekbeli kitűnő munkái hozták meg.
változós logaritmikus lineáris formákra jelentős eredményekre vezetne a diofantikus approximáció valamint a diofantikus egyenletek elméletében. Az áttörést, valamint Gelfond és Schneider 1. tételének, illetve Gelfond 2. tételének messzemenő kiterjesztéseit Alan Baker 1960-as évekbeli kitűnő munkái hozták meg.
Az alábbi tétel Baker [1], [2], [3] egyik meghatározó eredménye, mely tetszőleges 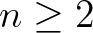 változós logaritmikus lineáris formák algebrai számok feletti lineáris függetlenségével kapcsolatos. Ez az eredmény kiterjesztése Gelfond és Schneider 1. tételének.
változós logaritmikus lineáris formák algebrai számok feletti lineáris függetlenségével kapcsolatos. Ez az eredmény kiterjesztése Gelfond és Schneider 1. tételének.
3. tétel. (Baker (1966,1967)) Legyen 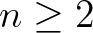 egy pozitív egész és legyenek
egy pozitív egész és legyenek 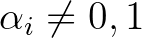 (
( 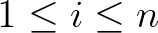 ) tetszőleges algebrai számok, valamint jelölje
) tetszőleges algebrai számok, valamint jelölje 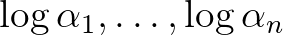 az
az 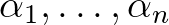 számok logaritmusainak a főértékét. Tegyük fel, hogy
számok logaritmusainak a főértékét. Tegyük fel, hogy 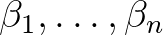 olyan tetszőleges algebrai számok, amelyek közül legalább egy nemnulla. Ha
olyan tetszőleges algebrai számok, amelyek közül legalább egy nemnulla. Ha 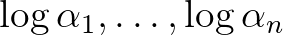 lineárisan függetlenek a racionális számtest fölött, akkor
lineárisan függetlenek a racionális számtest fölött, akkor

Megemlítjük még Baker [1] alábbi eredményét, amely kiterjesztése Gelfond 2. tételének tetszőleges 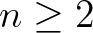 változós logaritmikus lineáris formákra. A tétel kimondásához használjuk egy
változós logaritmikus lineáris formákra. A tétel kimondásához használjuk egy 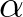 algebrai szám naív magasságának a fogalmát, ami nem más mint az
algebrai szám naív magasságának a fogalmát, ami nem más mint az 
 feletti definiáló polinomja együtthatói abszolútértékének a maximuma.
feletti definiáló polinomja együtthatói abszolútértékének a maximuma.
4. tétel. (Baker (1966)) Legyen 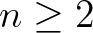 pozitív egész, és legyenek
pozitív egész, és legyenek 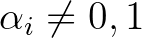 (
( 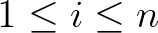 ) tetszőleges algebrai számok, valamint jelölje
) tetszőleges algebrai számok, valamint jelölje 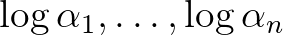 az
az 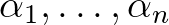 számok logaritmusainak a főértékét. Tegyük fel, hogy
számok logaritmusainak a főértékét. Tegyük fel, hogy 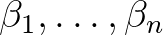 olyan algebrai számok, amelyek közül legalább egy nemnulla. Ha
olyan algebrai számok, amelyek közül legalább egy nemnulla. Ha 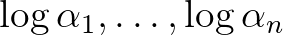 lineárisan függetlenek a racionális számtest fölött, akkor bármely
lineárisan függetlenek a racionális számtest fölött, akkor bármely 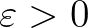 -hoz létezik egy
-hoz létezik egy 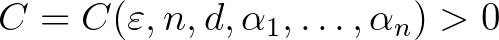 effektíve kiszámítható konstans úgy, hogy
effektíve kiszámítható konstans úgy, hogy
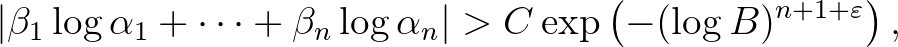
ahol 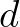 , illetve
, illetve 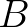 jelöli a
jelöli a 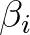 (
( 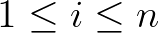 ) algebrai számok fokainak, illetve naív magasságainak egy felső korlátját.
) algebrai számok fokainak, illetve naív magasságainak egy felső korlátját.
Látható, hogy Baker fenti tételében az alsó korlát hasonló struktúrájú mint a 2. tételben, sőt az általános esetben a 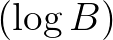 kitevőjében
kitevőjében  áll, ami némileg javítása az
áll, ami némileg javítása az 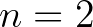 esetben szereplő
esetben szereplő 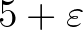 nagyságrendnek.
nagyságrendnek.
Két évvel Baker fenti tétele után Feldman [11] a 4. tétel alábbi javítását igazolta.
5. tétel. (Feldman (1968)) Legyen 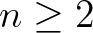 pozitív egész és legyenek
pozitív egész és legyenek 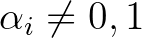 (
( 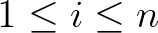 ) algebrai számok, valamint jelölje
) algebrai számok, valamint jelölje 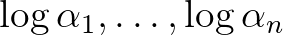 az
az 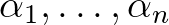 számok logaritmusainak a főértékét. Tegyük fel, hogy
számok logaritmusainak a főértékét. Tegyük fel, hogy 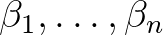 olyan algebrai számok, amelyek közül legalább egy nemnulla. Ha
olyan algebrai számok, amelyek közül legalább egy nemnulla. Ha 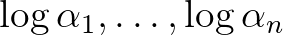 lineárisan függetlenek a racionális számtest fölött, akkor létezik egy
lineárisan függetlenek a racionális számtest fölött, akkor létezik egy  effektíve kiszámítható konstans úgy, hogy
effektíve kiszámítható konstans úgy, hogy
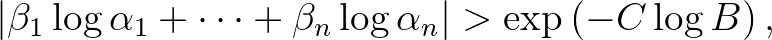
ahol 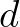 , illetve
, illetve 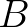 jelöli a
jelöli a 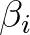 (
( 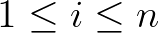 ) algebrai számok fokainak, illetve naív magasságainak egy felső korlátját.
) algebrai számok fokainak, illetve naív magasságainak egy felső korlátját.
Megjegyezzük, hogy az 5. tételben a 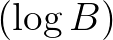 -től való függés éles, azaz ez nem gyengíthető tovább. A diofantikus egyenletekre való alkalmazáskor a
-től való függés éles, azaz ez nem gyengíthető tovább. A diofantikus egyenletekre való alkalmazáskor a 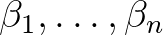 algebrai számok egészek és fontos még, hogy a
algebrai számok egészek és fontos még, hogy a 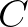 értéke explicit módon kiszámítható legyen.
értéke explicit módon kiszámítható legyen.
Ebben a tekintetben Baker [4] volt az első, aki 1968-ban Feldman fenti eredményének teljesen explicit verzióját igazolta.
6. tétel. (Baker (1968)) Legyen 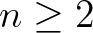 pozitív egész, legyenek
pozitív egész, legyenek 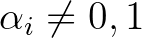 (
( 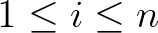 ) algebrai számok, valamint jelölje
) algebrai számok, valamint jelölje 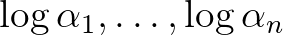 az
az 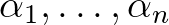 számok logaritmusainak a főértékét, és tegyük fel, hogy
számok logaritmusainak a főértékét, és tegyük fel, hogy  . Lgyenek továbbá
. Lgyenek továbbá 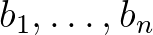 olyan egészek, amelyek közül legalább egy nemnulla, és legyen
olyan egészek, amelyek közül legalább egy nemnulla, és legyen 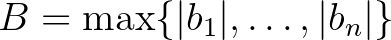 . Ha
. Ha
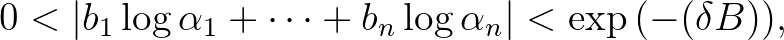
akkor
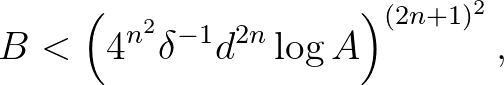
ahol 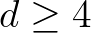 , illetve
, illetve 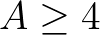 jelöli az
jelöli az 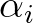 (
( 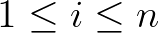 ) algebrai számok fokainak, illetve naív magasságainak egy felső korlátját.
) algebrai számok fokainak, illetve naív magasságainak egy felső korlátját.
Ezek után kiderült, hogy Baker logaritmikus lineáris formákra vonatkozó explicit tételei alkalmazhatók diofantikus egyenletek széles osztályaira. Nevezetesen, ezen tételek segítségével effektív felső korlátok nyerhetők jónéhány sokat vizsgált klasszikus diofantikus egyenletcsalád megoldásainak a méretére, úgy mint Thue-egyenletek [5], szuper- és hiperelliptikus egyenletek [8], Mordell-típusú egyenletek [6], [7], Schinzel–Tijdeman-egyenlet [24], Catalan-egyenlet [26], kétváltozós egységegyenletek [16], [17], diszkrimináns és indexforma egyenletek [15], szétesőforma egyenletek [18], lineáris binér rekurzív sorozatokkal kapcsolatos diofantikus egyenletek [22], [25] stb. Megjegyezzük, hogy ezeken a területeken a Győry Kálmán által alapított debreceni számelméleti iskola számos tagja ért el szép eredményeket (ld. pl. Győry Kálmán, Pethő Attila, Brindza Béla, Gaál István, Pintér Ákos, Hajdu Lajos, Bérczes Attila, Tengely Szabolcs, Pink István idevonatkozó munkáit).
Baker explicit eredményeit kombinálva egy – Baker és Davenport [9] által kidolgozott – redukciós eljárással, kiderült, hogy a 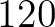 az egyetlen olyan pozitív egész szám, amellyel az
az egyetlen olyan pozitív egész szám, amellyel az 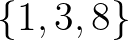 diofantikus hármas kiterjeszthető az
diofantikus hármas kiterjeszthető az 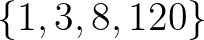 diofantikus négyessé.4 Ez a kiváló eredmény is megmutatta, hogy a Baker által kidolgozott módszer kombinálása bizonyos redukciós eljárásokkal kiválóan alkalmas lehet konkrét diofantikus egyenletek teljes megoldáshalmazának leírására. Nevezetesen, kombináljuk Baker fenti explicit tételét (pl. 6. tétel) vagy ezen tétel alábbiakban ismertetendő valamelyik javítását (pl. 7. Tétel) bizonyos redukciós eljárásokkal (pl. lánctört-algoritmus, Baker–Davenport redukciós algoritmus, LLL-algoritmus). Ezen a ponton megemlítjük Bugeaud [10] 2018-ban megjelent könyvét, amely egy kiváló áttekintő mű a Baker-módszerrel kapcsolatban.
diofantikus négyessé.4 Ez a kiváló eredmény is megmutatta, hogy a Baker által kidolgozott módszer kombinálása bizonyos redukciós eljárásokkal kiválóan alkalmas lehet konkrét diofantikus egyenletek teljes megoldáshalmazának leírására. Nevezetesen, kombináljuk Baker fenti explicit tételét (pl. 6. tétel) vagy ezen tétel alábbiakban ismertetendő valamelyik javítását (pl. 7. Tétel) bizonyos redukciós eljárásokkal (pl. lánctört-algoritmus, Baker–Davenport redukciós algoritmus, LLL-algoritmus). Ezen a ponton megemlítjük Bugeaud [10] 2018-ban megjelent könyvét, amely egy kiváló áttekintő mű a Baker-módszerrel kapcsolatban.
A cikk hátralevő részében először ismertetjük a nemnulla logaritmikus lineáris formákra vonatkozó, Matveevtől [20] származó jelenlegi legélesebb alsó becslést, majd egy konkrét példán keresztül megmutatjuk, hogy a 7. tétel és lánctört-algoritmus kombinációja milyen hatékony eszközként szolgál egy bizonyos diofantikus egyenlet összes megoldásának meghatározására.
Ehhez szükségünk lesz az alábbi jelölésekre. Egy 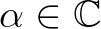 algebrai szám esetén jelölje továbbra is
algebrai szám esetén jelölje továbbra is ![$m_{\alpha}(x)=a_0x^k+a_1x^{k-1}+\ldots+a_k \in \mathbb{Z}[x]$](/images/stories/latexuj/2022-02/2022-02-abakermodszeresegyalkalmazasa/img4.png) (
(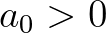 ,
, 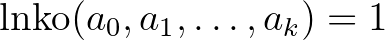 ) az
) az 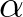 definiáló polinomját valamint legyenek
definiáló polinomját valamint legyenek 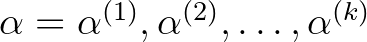 az
az 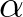 közönséges konjugáltjai (azaz az
közönséges konjugáltjai (azaz az 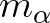 polinom
polinom 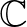 -beli gyökei). Ekkor
-beli gyökei). Ekkor 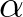 abszolút logaritmikus magasságán a
abszolút logaritmikus magasságán a
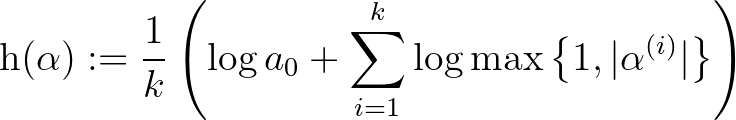
mennyiséget értjük.
Legyenek 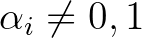 (
( 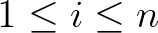 ) algebrai számok, és jelölje
) algebrai számok, és jelölje 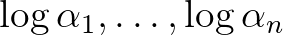 az
az 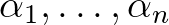 logaritmusainak a főértékét. Legyen
logaritmusainak a főértékét. Legyen 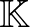 egy olyan algebrai számtest5, amely tartalmazza az
egy olyan algebrai számtest5, amely tartalmazza az 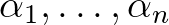 algebrai számokat, és legyen
algebrai számokat, és legyen ![$d=[\mathbb{K}:\mathbb{Q}]$](/images/stories/latexuj/2022-02/2022-02-abakermodszeresegyalkalmazasa/img91.png) . Tekintsük a
. Tekintsük a
logaritmikus lineáris formát, ahol 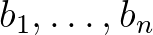 olyan egészek, amelyek közül legalább egy nemnulla. Legyen
olyan egészek, amelyek közül legalább egy nemnulla. Legyen
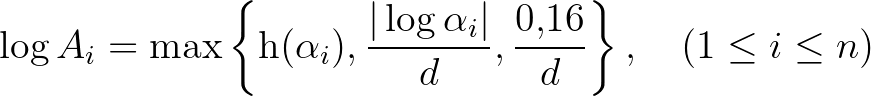
és
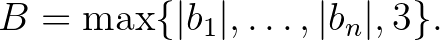
7. tétel. (Matveev (2000)) Ha (3)-ban 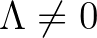 , akkor
, akkor
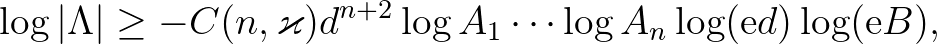
ahol 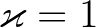 , ha
, ha 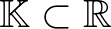 és
és 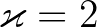 egyébként, valamint
egyébként, valamint
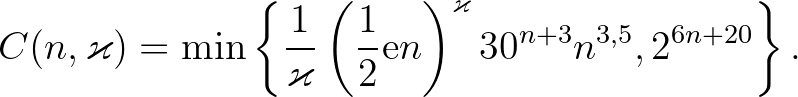
A továbbiakban megmutatjuk, hogy a 7. tétel és a lánctört-algoritmus kombinációja hogyan alkalmazható a Catalan-egyenlet egy speciális esetének a teljes megoldására. Szükségünk lesz még az alábbi jól ismert technikai lemmára.
Lemma. Ha 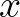 olyan valós szám, amelyre
olyan valós szám, amelyre 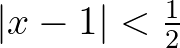 , akkor
, akkor 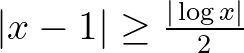 .
.
A cikk utolsó részében vizsgálatunk tárgyát az
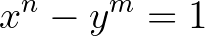
Catalan-egyenlet6 azon speciális esete képezi, amikor 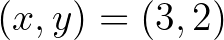 . Nevezetesen tekintsük a
. Nevezetesen tekintsük a
diofantikus egyenletet az 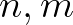 pozitív egész ismeretlenekkel. Világos, hogy az
pozitív egész ismeretlenekkel. Világos, hogy az 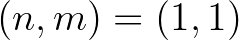 és
és 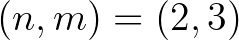 megoldásai a (4) egyenletnek. A 7. tételt a lánctört-algoritmussal kombinálva megmutatjuk, hogy a fentieken kívül nincs is más megoldás, azaz az
megoldásai a (4) egyenletnek. A 7. tételt a lánctört-algoritmussal kombinálva megmutatjuk, hogy a fentieken kívül nincs is más megoldás, azaz az 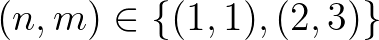 a (4) összes megoldása a pozitív egészek körében.
a (4) összes megoldása a pozitív egészek körében.
Tegyük fel, hogy 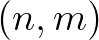 egy megoldása a (4) egyenletnek. Elemi nagyságrendi meggondolással adódik, hogy
egy megoldása a (4) egyenletnek. Elemi nagyságrendi meggondolással adódik, hogy
A (4) egyenlet mindkét oldalát 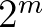 -nel osztva, és abszolút értéket véve, kapjuk, hogy
-nel osztva, és abszolút értéket véve, kapjuk, hogy
A továbbiakban két esetet különböztetünk meg aszerint, hogy (6)-ban
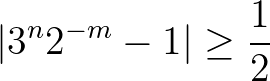 vagy
vagy 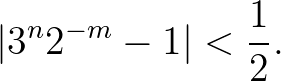
Ha 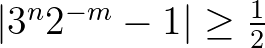 , akkor (6) azt implikálja, hogy
, akkor (6) azt implikálja, hogy

amiből  adódik. Ez viszont (5) miatt éppen az
adódik. Ez viszont (5) miatt éppen az 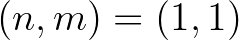 megoldást adja.
megoldást adja.
Tegyük most fel, hogy 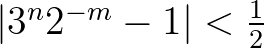 . A Lemmát az
. A Lemmát az  választással alkalmazva azt nyerjük, hogy
választással alkalmazva azt nyerjük, hogy 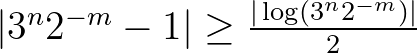 , ami (6) miatt az
, ami (6) miatt az
egyenlőtlenségre vezet. Jelölje  a (7) bal oldalán szereplő
a (7) bal oldalán szereplő
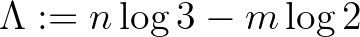
logaritmikus lineáris formát. Ekkor (7)-ből azt kapjuk, hogy
Ha most 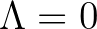 lenne, akkor
lenne, akkor 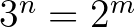 adódna, ami
adódna, ami 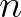 és
és 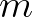 pozitív egész volta miatt lehetetlen. Ezért a továbbiakban feltehető, hogy
pozitív egész volta miatt lehetetlen. Ezért a továbbiakban feltehető, hogy 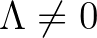 . A célunk az, hogy a Baker-módszer felhasználásával nemtriviális alsó becslést nyerjünk a
. A célunk az, hogy a Baker-módszer felhasználásával nemtriviális alsó becslést nyerjünk a  mennyiségre. Ehhez alkalmazzuk a 7. tételt az alábbi paraméterekkel:
mennyiségre. Ehhez alkalmazzuk a 7. tételt az alábbi paraméterekkel: 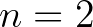 ,
, 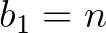 ,
, 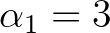 ,
,  ,
, 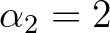 ,
, 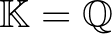 ,
, 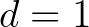 ,
, 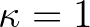 . Mivel
. Mivel 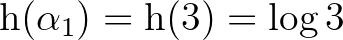 és
és 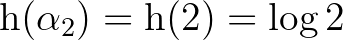 , ezért a
, ezért a 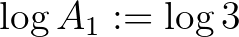 és
és 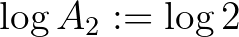 választás megfelelő. Továbbá (5) miatt élhetünk a
választás megfelelő. Továbbá (5) miatt élhetünk a 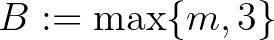 választással. Így a 7. tétel miatt adódik, hogy
választással. Így a 7. tétel miatt adódik, hogy
Végül, a (8) és (9) összevetéséből az
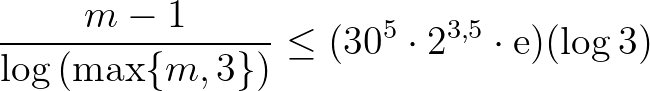
következik, amiből egyszerű számolás után adódik, hogy
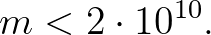
Azt kaptuk tehát, hogy ha a (4) egyenletnek van olyan  megoldása, melyre
megoldása, melyre
akkor
Ez egyrészt igen ígéretes, hiszen az ismeretlenek méretére kapott felső korlát teljesen explicit, másrészt viszont túl nagy ahhoz, hogy (4) megoldásait a (11) korlát alatt direkt módon le tudjuk számolni és meg tudjuk határozni. Ezért szükséges a (11) korlát redukálása, melyhez a lánctört-algoritmust hívjuk segítségül. A (7) mindkét oldalát 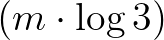 -mal leosztva az
-mal leosztva az
egyenlőtlenséghez jutunk.
Ha 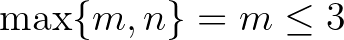 , akkor a (4) egyenlet (10) feltételnek eleget tevő összes
, akkor a (4) egyenlet (10) feltételnek eleget tevő összes 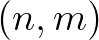 megoldása triviálisan leszámlálható. Azt kapjuk, hogy
megoldása triviálisan leszámlálható. Azt kapjuk, hogy 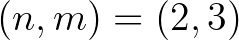 az egyetlen ilyen megoldás.
az egyetlen ilyen megoldás.
Tegyük fel végül, hogy 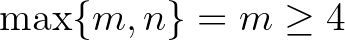 . Ekkor
. Ekkor  , és ezért Legendre egy tétele (ld. [12], 368. oldal, 2. Megjegyzés) és (12) miatt azt nyerjük, hogy
, és ezért Legendre egy tétele (ld. [12], 368. oldal, 2. Megjegyzés) és (12) miatt azt nyerjük, hogy  szükségképpen a
szükségképpen a 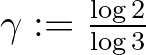 valós szám egy közelítő törtje. Ezt kombinálva (11)-gyel azt kapjuk, hogy a (4) egyenlet (10) feltételt kielégítő
valós szám egy közelítő törtje. Ezt kombinálva (11)-gyel azt kapjuk, hogy a (4) egyenlet (10) feltételt kielégítő 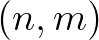 megoldása a
megoldása a 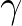 azon közelítő törtjei közül kerülhet ki, amelyekre
azon közelítő törtjei közül kerülhet ki, amelyekre
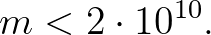
Ilyen közelítő törtből viszont kevés van. Egy gyors számítógépes ellenőrzés mutatja, hogy a 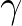
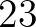 -adik konvergensének a nevezője már nagyobb, mint
-adik konvergensének a nevezője már nagyobb, mint 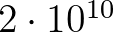 , ezért elegendő a
, ezért elegendő a 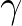 első
első 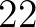 darab konvergensét kiszámolni. További gyors számítógépes vizsgálat igazolja, hogy ezen 22 darab
darab konvergensét kiszámolni. További gyors számítógépes vizsgálat igazolja, hogy ezen 22 darab 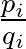 (
(  ) konvergensre fennáll, hogy
) konvergensre fennáll, hogy

amiből persze
is következik. Végül a (12) és (13) összefüggéseket kombinálva azt nyerjük, hogy
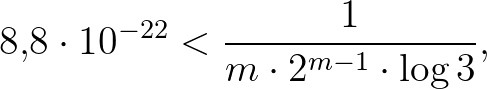
amiből 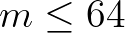 adódik. A
adódik. A 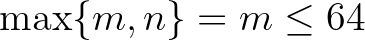 felső korlát már elegendően kicsi ahhoz, hogy a (4) egyenlet
felső korlát már elegendően kicsi ahhoz, hogy a (4) egyenlet  és
és 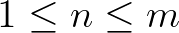 feltételeknek eleget tevő
feltételeknek eleget tevő 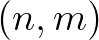 megoldásait megadjuk. Kiderül, hogy ilyen megoldás nincs. Ezért a (4) egyenlet összes megoldása a pozitív egészekre nézve éppen az
megoldásait megadjuk. Kiderül, hogy ilyen megoldás nincs. Ezért a (4) egyenlet összes megoldása a pozitív egészekre nézve éppen az 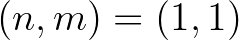 és
és 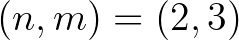 .
.
A fenti kidolgozott példa is jól tükrözi, hogy milyen erős eszköz a Baker-módszer a diofantikus egyenletek elméletében. Segítségével nagy, de teljesen explicit felső korlátok nyerhetők bizonyos diofantikus egyenletek megoldásainak méretére. Végül az így kapott Baker-típusú korlátokat valamilyen hatékony redukciós eljárással (pl. lánctört-algoritmus, Baker–Davenport-algoritmus, LLL-algoritmus) redukálva leírható ezen diofantikus egyenletek teljes megoldáshalmaza.
Irodalomjegyzék
- [1] A. Baker, Linear forms in the logarithms of algebraic numbers. I, Mathematika 12 (1966), 204–216.
[2] A. Baker, Linear forms in the logarithms of algebraic numbers. II, Mathematika 14 (1967), 102–107.
[3] A. Baker, Linear forms in the logarithms of algebraic numbers. III, Mathematika 14 (1967), 220–228.
[4] A. Baker, Linear forms in the logarithms of algebraic numbers. IV, Mathematika 15 (1968), 204–216.
[5] A. Baker, Contributions to the theory of Diophantine equations. I. On the representation of integers by binary forms, Phil. Trans. Royal Soc. London A263 (1968), 173–191.
[6] A. Baker, Contributions to the theory of Diophantine equations. II. The Diophantine equation 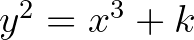 , Phil. Trans. Royal Soc. London A263 (1968), 193–208.
, Phil. Trans. Royal Soc. London A263 (1968), 193–208.
[7] A. Baker, The diophantine equation 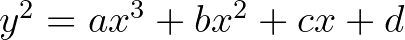 , J. London Math. Soc. 43 (1968), 1–9.
, J. London Math. Soc. 43 (1968), 1–9.
[8] A. Baker, Bounds for the solutions of the hyperelliptic equation, Proc. Cambridge Phil. Soc. 65 (1969), 439–444.
[9] A. Baker and H. Davenport, The equations 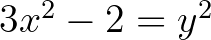 and
and 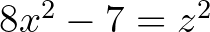 , Quart. J. Math. Oxford (2) 20 (1969), 129–137.
, Quart. J. Math. Oxford (2) 20 (1969), 129–137.
[10] Y. Bugeaud, Linear forms in logarithms and applications, IRMA Lectures in Mathematics and Theoretical Physics 28, European Mathematical Society, 2018.
[11] N. I. Feldman, Improved estimate for a linear form of the logarithms of algebraic numbers, Mat. Sb. 77 (1968), 256–270 (in Russian). English translation in Math. USSR. Sb. 6 (1968) 393–406.
[12] Freud Róbert és Gyarmati Edit, Számelmélet, Nemzeti Tankönyvkiadó, 2006.
[13] A. O. Gelfond, On Hilbert’s seventh problem, Dokl. Akad. Nauk SSSR 2 (1934), 1–3 (in Russian) and 4–6 (in French) Sur le septième problème de Hilbert, Izv. Akad. Nauk SSSR 7 (1934), 623–630.
[14] A. O. Gelfond, Sur les approximations des nombres transcendants par des nombres algébriques, C. R. Acad. Sc. URSS 2 (1935), 177–182.
[15] K. Győry, Sur les polynomes ä coefficients entiers et de discriminant donne III, Publ. Math. Debrecen 23 (1976), 141-165.
[16] K. Győry, On the number of solutions of linear equations in units of an algebraic number field, Comment. Math. Helv. 54 (1979), 583–600.
[17] K, Győry, On the solutions of linear diophantine equations in algebraic integers of bounded norm, Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 22/23 (1980), 225–233.
[18] K. Győry, Bounds for the solutions of decomposable form equations, Publ. Math. Debrecen 52 (1998), 1-31.
[19] J. Liouville, Remarques relatives à des classes très étendues de quantités dont la valeur n’est ni algébrique, ni même réductible à des irrationnelles algébriques, C. R. Acad. Sci. Paris 18 (1844), 883–885 et 910–911.
[20] E. M. Matveev, An explicit lower bound for a homogeneous rational linear form in logarithms of algebraic numbers. II, Izv. Ross. Acad. Nauk Ser. Mat. 64 (2000), 125–180 (in Russian); English translation in Izv. Math. 64 (2000), 1217–1269.
[21] P. Mihailescu, Primary cyclotomic units and a proof of Catalan's conjecture, J. Reine Angew. Math. 572 (2004), 167–195.
[22] A. Pethő, Diophantine properties of linear recursive sequences. II, Acta Math. Acad. Paedagog. Nyházi. (N.S.) 17 (2001), 81–96.
[23] Th. Schneider, Transzendenzuntersuchungen periodischer Funktionen, J. Reine Angew. Math. 172 (1934), 65–74.
[24] A. Schinzel and R. Tijdeman, On the equation  Acta Arithmetica 31 (1976), 199-204.
Acta Arithmetica 31 (1976), 199-204.
[25] T. N. Shorey and C. L. Stewart, On the Diophantine equation  and pure powers in recurrence sequences, Math. Scand. 52 (1983), 24–36.
and pure powers in recurrence sequences, Math. Scand. 52 (1983), 24–36.
[26] R. Tijdeman, On the equation of Catalan, Acta Arithmetica 29 (1976) , 197-209.
[27] A. Wiles, Modular elliptic curves and Fermat's last theorem, Ann. of Math. (2) 141 (1995), no. 3, 443–551.
Lábjegyzetek
- 1 A valós logaritmusfüggvény kiterjeszthető
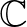 -re, ami érdekes módon
-re, ami érdekes módon 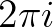 szerint periodikus lesz.
szerint periodikus lesz. - 2 A
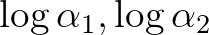 számokat lineárisan függetlennek nevezzük a racionális számtest fölött, ha
számokat lineárisan függetlennek nevezzük a racionális számtest fölött, ha 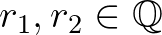 ,
, 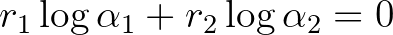 -ból következik, hogy
-ból következik, hogy 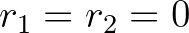 . Általánosabban, a
. Általánosabban, a 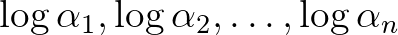 számokat lineárisan függetlennek nevezzük a racionális számtest fölött, ha
számokat lineárisan függetlennek nevezzük a racionális számtest fölött, ha 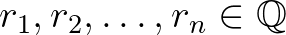 ,
, 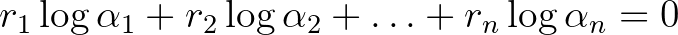 -ból következik, hogy
-ból következik, hogy 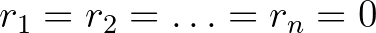 .
. - 3 A területen megszokott szóhasználat szerint ez azt jelenti, hogy
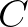 értéke a paraméterek rögzítése után explicit módon kiszámolható.
értéke a paraméterek rögzítése után explicit módon kiszámolható. - 4
- Pozitív egészek egy
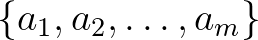 halmazát diofantikus
halmazát diofantikus 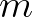 -esnek nevezzük, ha
-esnek nevezzük, ha  teljes négyzet minden
teljes négyzet minden  esetén.
esetén. - 5 Az algebrai számtest egy olyan test, melynek minden eleme algebrai szám.
- 6 1844-ben Eugène Charles Catalan belga matematikus a neves Crelle folyóirat szerkesztõjéhez írt levelében az alábbi sejtést fogalmazta meg: A természetes számok növekvõ sorrendbe rendezett teljes hatványaiból álló
 ,
, 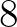 ,
, 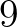 ,
, 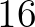 ,
, 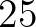 ,
,  ,
, 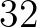 ,
, 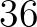 ,
, 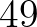 ,
, 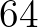 ,
, 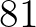 ,
, 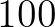 ,
, 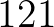 ,
, 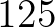 ,
,  ,
, 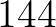 ,
, 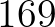 , ... sorozatában egyetlen olyan pár van, amelyek különbsége
, ... sorozatában egyetlen olyan pár van, amelyek különbsége 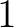 . Ez a pár a
. Ez a pár a 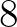 és a
és a 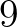 . A fenti sejtés ekvivalens módon átfogalmazható exponenciális diofantikus egyenletek segítségével, ami a szakirodalomban Catalan-sejtés (Catalan-egyenlet) néven vált ismertté. Nevezetesen, az
. A fenti sejtés ekvivalens módon átfogalmazható exponenciális diofantikus egyenletek segítségével, ami a szakirodalomban Catalan-sejtés (Catalan-egyenlet) néven vált ismertté. Nevezetesen, az 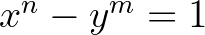 egyenletet, ahol
egyenletet, ahol 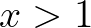 ,
, 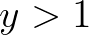 ,
,  ,
, 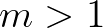 ismeretlen egészek, Catalan-egyenletnek nevezzük. A Catalan-sejtés szerint ezen egyenlet egyetlen megoldása
ismeretlen egészek, Catalan-egyenletnek nevezzük. A Catalan-sejtés szerint ezen egyenlet egyetlen megoldása 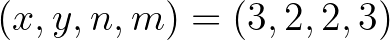 . A Baker-módszer felhasználásával Tijdeman [26] 1976-ban effektív felső korlátot nyert
. A Baker-módszer felhasználásával Tijdeman [26] 1976-ban effektív felső korlátot nyert 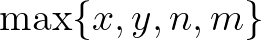 -re, míg Mihailescu [21] 2004-ben teljes egészében igazolta a sejtést.
-re, míg Mihailescu [21] 2004-ben teljes egészében igazolta a sejtést.