Az euklideszi geometriában, egy  feletti vektortérben a hosszúságok és a szögek a legfontosabb mérőszámok, és a dolgok merevek. A szimplektikus geometriában a kétdimenziós mérőszámok a kulcsszereplők, és a komplex számok a természetes skalárok. Kiderül, hogy a szimplektikus struktúrák sokkal rugalmasabbak, mint a komplex függvénytan holomorf függvényei, vagy a Riemann-geometria metrikái.
feletti vektortérben a hosszúságok és a szögek a legfontosabb mérőszámok, és a dolgok merevek. A szimplektikus geometriában a kétdimenziós mérőszámok a kulcsszereplők, és a komplex számok a természetes skalárok. Kiderül, hogy a szimplektikus struktúrák sokkal rugalmasabbak, mint a komplex függvénytan holomorf függvényei, vagy a Riemann-geometria metrikái.
A „szimplektikus” szó Hermann Weylnek a csoportokról szóló klasszikus könyvében bevezetett kifejezés tükörfordítása. A szó valójában a komplex görög megfelelője, azaz a latin com-plexus (egybefonva) szóösszetétel tagonkénti görög fordítása:
συμ – πλεκτικοζ.
Weyl annak a Lie-csoportnak a jelölésére javasolta ezt a szót, amely megtartja a nemelfajuló ferdén szimmetrikus bilineáris formát. Ezt megelőzően a szóbanforgó Lie-csoportot „egyenes komplex csoportnak” vagy „abeli lineáris csoportnak” nevezték (arra utalva, hogy Abel is tanulmányozta ezt a csoportot).
Egy (valós)  sokaságon lévő
sokaságon lévő 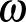 2-forma olyan matematikai objektum, amely minden
2-forma olyan matematikai objektum, amely minden 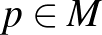 pontban két érintővektort kap változóként, és ezekre egy valós számot ad, mégpedig ferdén szimmetrikus és bilineáris módon. Pontosabban,
pontban két érintővektort kap változóként, és ezekre egy valós számot ad, mégpedig ferdén szimmetrikus és bilineáris módon. Pontosabban, 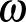 egy
egy
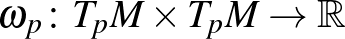
ferdén szimmetrikus leképezés-családot ad meg, amely 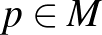 -től sima módon függ. Az
-től sima módon függ. Az 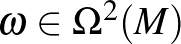 2-forma szimplektikus, ha zárt (vagyis külső deriváltja,
2-forma szimplektikus, ha zárt (vagyis külső deriváltja, 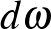 teljesíti a
teljesíti a  egyenletet) és nemelfajuló, vagyis minden
egyenletet) és nemelfajuló, vagyis minden 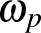 nemelfajuló. Ez utóbbi feltétel ekvivalens avval, hogy minden nemnulla
nemelfajuló. Ez utóbbi feltétel ekvivalens avval, hogy minden nemnulla 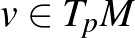 érintővektornak van egy szimplektikus „barátja”, vagyis egy olyan
érintővektornak van egy szimplektikus „barátja”, vagyis egy olyan 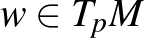 vektor, amelyre
vektor, amelyre  . Egy szimplektikus sokaság pedig egy
. Egy szimplektikus sokaság pedig egy  szimplektikus formával ellátott (valós)
szimplektikus formával ellátott (valós)  sokaság.
sokaság.
A nemelfajulóságnak fontos következményei vannak. Tisztán lineáris algebrai alapon, a Gram–Schmidt-eljárás ferdén szimmetrikus analógját alkalmazva, minden  pontban kiválaszthatjuk
pontban kiválaszthatjuk 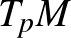 -nek egy
-nek egy 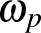 -vel kompatibilis bázisát. A bázis keresését egy
-vel kompatibilis bázisát. A bázis keresését egy  nemnulla vektorral kezdjük, majd megkeressük ennek
nemnulla vektorral kezdjük, majd megkeressük ennek 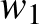 szimplektikus barátját. E két vektor a ferde szimmetria miatt lineárisan független. Ezután lehasítjuk a
szimplektikus barátját. E két vektor a ferde szimmetria miatt lineárisan független. Ezután lehasítjuk a  és
és 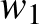 által kifeszített kétdimenziós alteret, és rekurzívan folytatjuk az eljárást, míg egy
által kifeszített kétdimenziós alteret, és rekurzívan folytatjuk az eljárást, míg egy
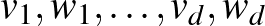
bázist nem kapunk, ami páros sok báziselemet tartalmaz. Tehát a szimplektikus sokaságok páros dimenziósak. A fenti gondolatmenet alapján minden érintőtérre gondolhatunk komplex vektortérként is, ahol 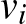 és
és 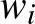 egy komplex alteret feszítenek ki. Az
egy komplex alteret feszítenek ki. Az  legmagasabb ék-hatvány sehol sem tűnik el, hiszen minden érintőtéren
legmagasabb ék-hatvány sehol sem tűnik el, hiszen minden érintőtéren

Másszóval, 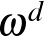 egy térfogati forma, így
egy térfogati forma, így  szükségképp irányítható. A szimplektikus geometriának fontos kapcsolatai vannak az algebrai kombinatorika, az algebrai geometria, dinamika, matematikai fizika és reprezentációelmélet felé. Az ezen kapcsolatokat mutató legfontosabb példák a következők:
szükségképp irányítható. A szimplektikus geometriának fontos kapcsolatai vannak az algebrai kombinatorika, az algebrai geometria, dinamika, matematikai fizika és reprezentációelmélet felé. Az ezen kapcsolatokat mutató legfontosabb példák a következők:
(1) 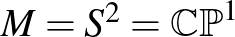 , és
, és 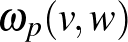 a
a 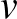 és
és 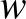 által meghatározott paralellogramma előjeles területe;
által meghatározott paralellogramma előjeles területe;
(2)  egy, az 1. ábrán mutatott tetszőleges Riemann-felület, és
egy, az 1. ábrán mutatott tetszőleges Riemann-felület, és 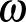 az (1)-ben megismert területi forma;
az (1)-ben megismert területi forma;

1. ábra. A területi forma egy Riemann-felületen szimplektikus geometriát definiál.
(3) 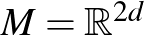 és
és 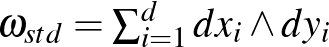 ; ezt a formát standard szimplektikus formának is nevezik.
; ezt a formát standard szimplektikus formának is nevezik.
(4) 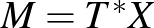 , az
, az 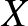 sokaság koérintő nyalábja, amire fázistérként tekintünk, a
sokaság koérintő nyalábja, amire fázistérként tekintünk, a 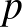 -koordináták
-koordináták 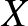 -ben a helyet jelölik, a
-ben a helyet jelölik, a 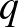 -koordináták pedig a koérintő irányban a momentumot, és
-koordináták pedig a koérintő irányban a momentumot, és 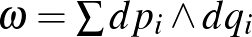
(5)  egy sima komplex projektív varietás, és
egy sima komplex projektív varietás, és 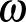 -t a Fubini–Study-forma indukálja (ez a példa magában foglalja a sima normális tórikus varietásokat is);
-t a Fubini–Study-forma indukálja (ez a példa magában foglalja a sima normális tórikus varietásokat is);
(6) 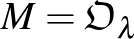 egy kompakt, összefüggő féligegyszerű
egy kompakt, összefüggő féligegyszerű 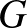 Lie csoport koadjungált orbitja, amelyet az
Lie csoport koadjungált orbitja, amelyet az 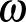 Kostant–Kirillov–Souriau-formával látunk el. A
Kostant–Kirillov–Souriau-formával látunk el. A 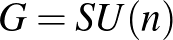 választással ezek a példák magukban foglalják a
választással ezek a példák magukban foglalják a 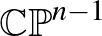 komplex projektív tereket, a
komplex projektív tereket, a 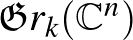 Grassmann-sokaságokat és az
Grassmann-sokaságokat és az 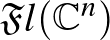 teljes zászlósokaságokat, továbbá az összes részleges zászlósokaságokat is.
teljes zászlósokaságokat, továbbá az összes részleges zászlósokaságokat is.
Számos irányítható sokaság nem hordoz szimplektikus struktúrát. Például a páros, legalább 4-dimenziós gömbök nem szimplektikusak. Ennek oka az, hogy egy kompakt sokaságon Stokes tétele biztosítja, hogy ![$[\omega]\neq 0\in H^2(M;\mathbb{R})$](/images/stories/latexuj/2022-02/2022-02-miisszimplektikusgeometria/img40.png) . Másszóval egy kompakt szimplektikus sokaságnak szükségképpen van nemtriviális 2-dimenziós kohomológiája..
. Másszóval egy kompakt szimplektikus sokaságnak szükségképpen van nemtriviális 2-dimenziós kohomológiája.. 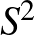 az egyetlen ilyen gömb.
az egyetlen ilyen gömb.
A (3) példa különösen érdekes Gaston Darboux tizenkilencedik századi matematikus differenciálformákra vonatkozó munkája alapján. Munkájának egy következménye
Darboux tétele. Legyen  egy
egy 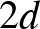 -dimenziós sokaság
-dimenziós sokaság 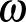 szimplektikus formával. Ekkor minden
szimplektikus formával. Ekkor minden 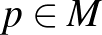 pontra létezik egy olyan
pontra létezik egy olyan 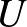 ,
, 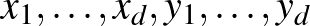 koordinátákkal ellátott térkép, hogy ezen
koordinátákkal ellátott térkép, hogy ezen
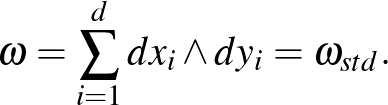
Ez a tétel pontosítja azt az állítást, hogy a szimplektikus geometria flexibilis/rugalmas. A Riemann-geometriában lokális invariánsok (mint például a görbület) különböztetik meg a metrikákat. Darboux tétele szerint lokálisan minden szimplektikus forma identikus. Ilymódon csak olyan globális topologikus kérdések maradnak, mint Mi egy adott szimplektikus sokaság kohomológia-gyűrűje?, vagy a finomabb, szimplektikus kérdés: Milyen nagy lehet egy adott szimplektikus sokaságon egy Darboux-térkép?.
Az 1970-es és 80-as években kifejlesztett két eszköz drámai fejlődést tett lehetővé a szimplektikus geometriában és a topológiában. Marsden és Weinstein, Atiyah, valamint Guillemin és Sternberg a momentumleképezés tulajdonságait leírva megoldhatóvá tették az első, kohomológiákra vonatkozó kérdést. Gromov pedig pszeudoholomorf görbék bevezetésével adott eszközt a második típusú kérdések megtámadására. Nézzünk néhány példát mindkét fajta problémára.
Amennyiben egy szimplektikus sokaságon egy Lie-csoport hatásában megmutatkozó szimmetria figyelhető meg, akkor a sokaság ellátható egy momentumleképezéssel. Ez megmaradó mennyiségeket ad, például a perdületet. A 2-dimenziós gömbfelületen értelmezett magasságfüggvény (ld. a 2. ábrát) adja az első pélát egy ilyen leképezésre.
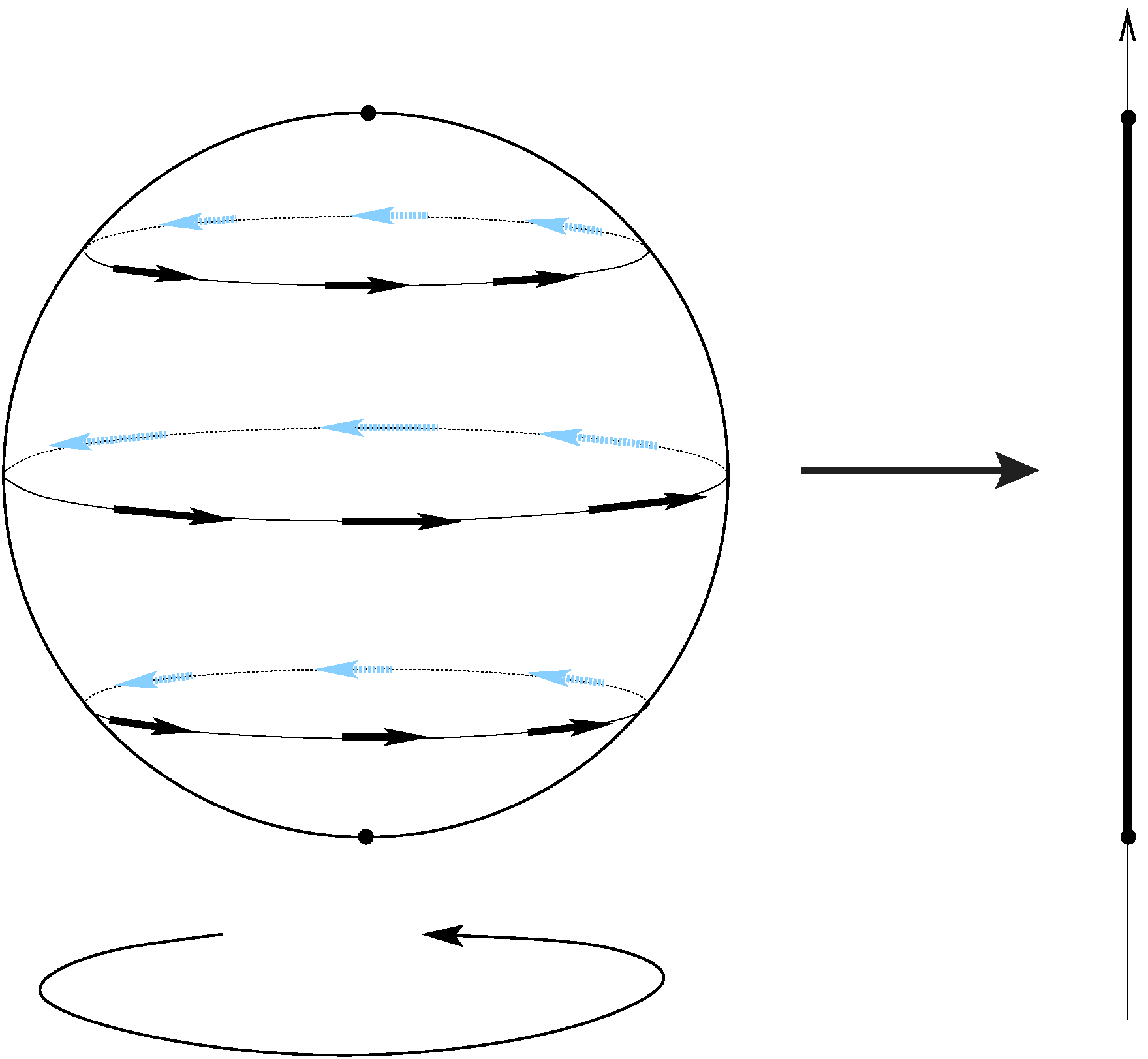
2. ábra. Az  körvonalnak az
körvonalnak az  gömbön való forgatások menti hatásához tartozó momentumleképezés.
gömbön való forgatások menti hatásához tartozó momentumleképezés.
Ez esetben a megmaradó mennyiség épp a perdület, és a magasságfüggvény egyszerű példáját adja egy perfekt Morse-függvénynek  -n. Amennyiben a Lie-csoport az
-n. Amennyiben a Lie-csoport az 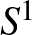 körvonal
körvonal 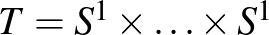 hatványa, azt mondjuk, hogy a sokaság egy Hamilton-féle
hatványa, azt mondjuk, hogy a sokaság egy Hamilton-féle 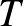 -tér, a momentumleképezést pedig
-tér, a momentumleképezést pedig 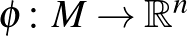 jelöli. 1982-ben Atiyah, és tőle függetlenül Guillemin és Sternberg a következő konvexitási tételt látta be (ld. a 3. ábrát):
jelöli. 1982-ben Atiyah, és tőle függetlenül Guillemin és Sternberg a következő konvexitási tételt látta be (ld. a 3. ábrát):
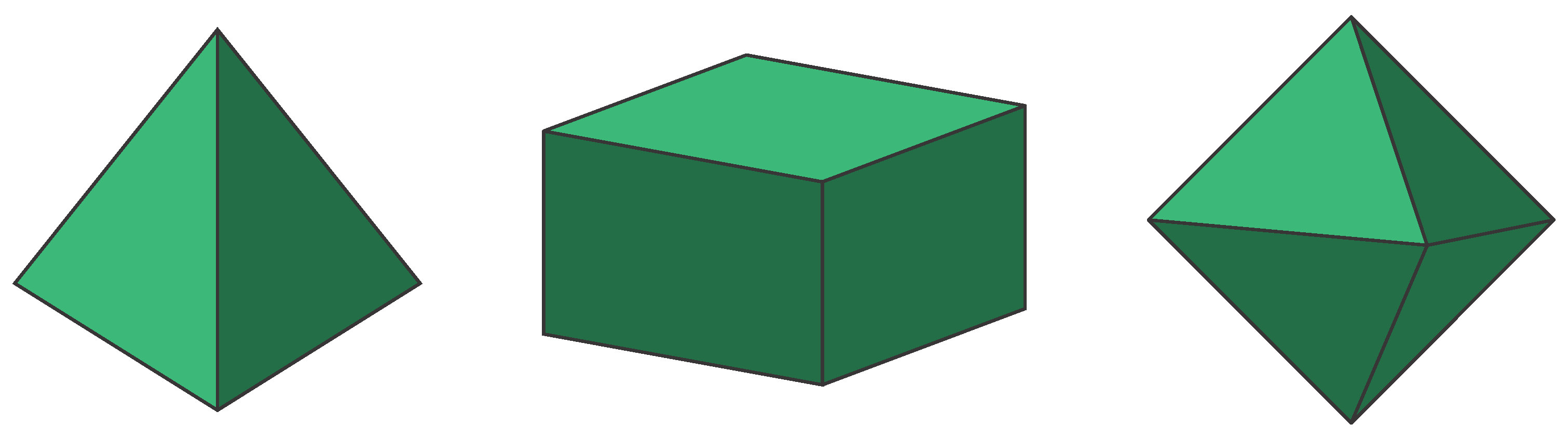
3. ábra. Atiyah és Guillemin-Sternberg belátták, hogy amennyiben egy szimplektikus sokaság bizonyos szimmetriáknak tesz eleget, úgy a momentumleképezésnél származó képe egy konvex politóp.
Konvexitási tétel. Egy  kompakt Hamilton-féle
kompakt Hamilton-féle 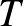 -tér esetén a
-tér esetén a 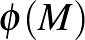 kép egy konvex politóp, amely épp az
kép egy konvex politóp, amely épp az 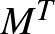
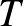 -fixpontok
-fixpontok 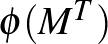 képének konvex burka.
képének konvex burka.
E tétel szoros kapcsolatot teremt egyrészt a szimplektikus és az algebrai geometria, másrészt a diszkrét geometria és a kombinatorika között. Atiyah bizonyítása azt is megmutatja, hogy a momentumleképezés (Bott értelmében) Morse-függvényt ad  -en, így a differenciáltopológia eszköztárát is elérhetővé teszi ahhoz, hogy
-en, így a differenciáltopológia eszköztárát is elérhetővé teszi ahhoz, hogy  globális topológiai tulajdonságait megértsük. Momentumleképezéseket szimplektikus hányadosok készítéséhez is használni lehet.
globális topológiai tulajdonságait megértsük. Momentumleképezéseket szimplektikus hányadosok készítéséhez is használni lehet.
(2) példánk szerint a kétdimenziós szimplektikus geometria nem más, mint területmegőrző geometria. Mivel egy szimplektikus forma egy térfogati formát ad, természetesen vetődik fel a kérdés, hogy magasabb dimenziókban is így van-e ez, vajon a szimplektikus geometria ott is ugyanolyan flexibilis, mint a térfogatmegőrző geometria: egy szimplektikus sokaság bárhogy nyújtható és/vagy összenyomható, feltéve, hogy a térfogatát megőrizzük? Pszeudoholomorf görbék alkalmazásával Gromov megmutatta, hogy ez nem így van, a szimplektikus leképezések sokkal merevebbek, mint térfogatmegőrző társaik. Jelölje 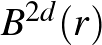 az
az 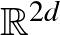 térben lévő
térben lévő  sugarú golyót. 1985-ben Gromov belátta nevezetes összenyomhatatlansági tételét (ld. a 4. ábrát):
sugarú golyót. 1985-ben Gromov belátta nevezetes összenyomhatatlansági tételét (ld. a 4. ábrát):
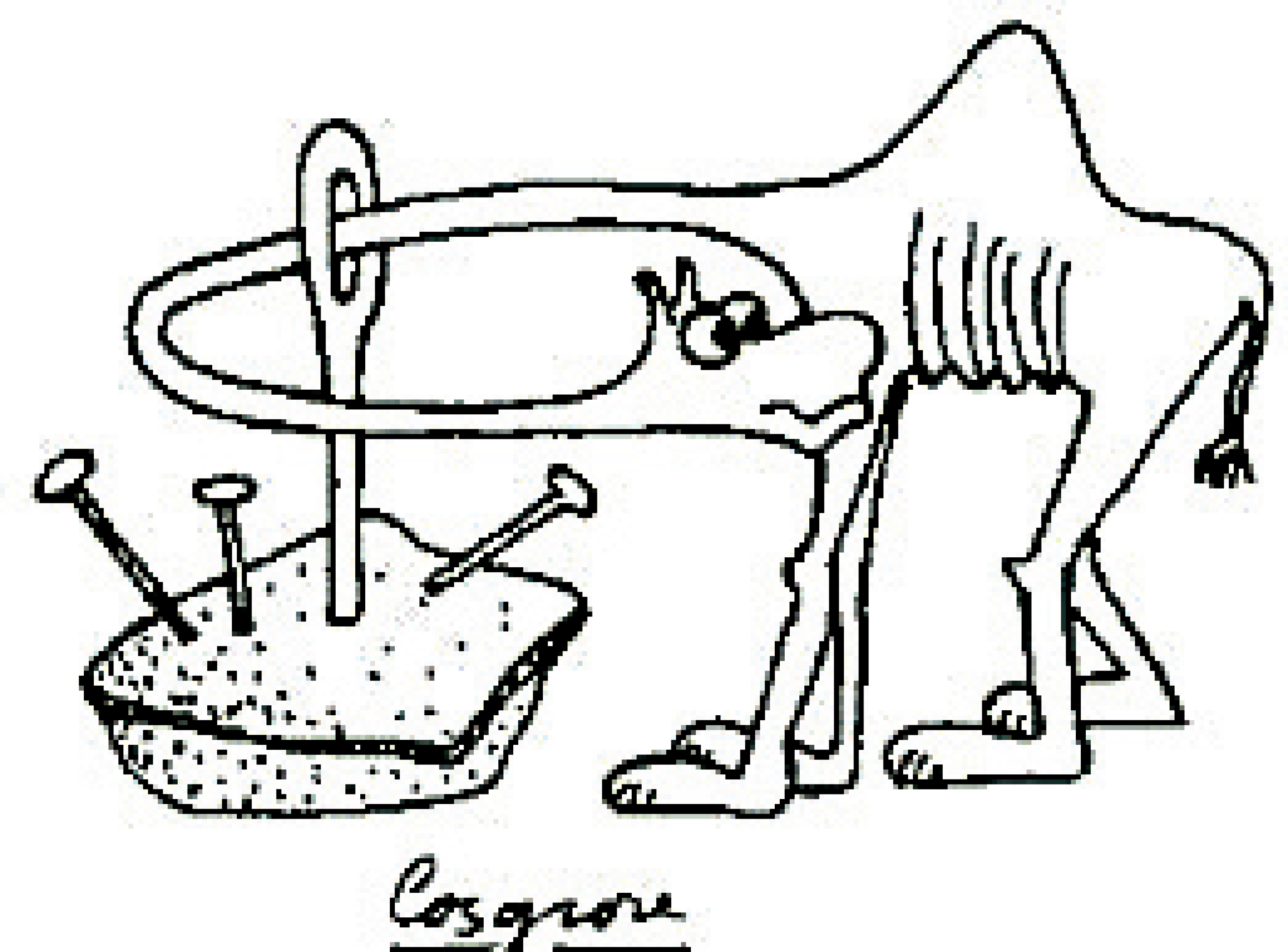
4. ábra. Az összenyomhatatlansági tétel geometriai tartalmat ad annak az állításnak, hogy egy teve nem tud átbújni a tű fokán: egy szimplektikus teve nem fér bele egy olyan térbe, amelynek egyik kétdimenziós iránya nagyon szűk, függetlenül attól, hogy a többi irányban mekkora a tér. Cosgrove grafikája eredetileg Ian Stewart „A szimplektikus teve” című cikkében jelent meg (1987, Nature) – köszönjük, hogy itt ismét felhasználhatjuk.
Összenyomhatatlansági tétel. Pontosan akkor létezik egy olyan 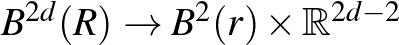 beágyazás, mely megőrzi az
beágyazás, mely megőrzi az 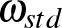 standard szimplektikus formát, ha
standard szimplektikus formát, ha  .
.
A tétel egyik iránya világos: ha  , akkor a megkívánt beágyazás nyilván létezik. Hogy megtalálja egy ilyen leképezés akadályát, Gromov egy
, akkor a megkívánt beágyazás nyilván létezik. Hogy megtalálja egy ilyen leképezés akadályát, Gromov egy 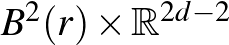 -beli pszeudoholomorf görbét és a szimplektikus beágyazást használta ahhoz, hogy egy
-beli pszeudoholomorf görbét és a szimplektikus beágyazást használta ahhoz, hogy egy  -beli minimális felületet adjon, ami már kikényszeríti az
-beli minimális felületet adjon, ami már kikényszeríti az  egyenlőtlenséget. Másrészt viszont nyilván minden
egyenlőtlenséget. Másrészt viszont nyilván minden  és
és 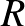 választásra létezik térfogatmegőrző leképezés. Informálisan szólva, a szimplektikus teve nem tud átbújni a tű fokán. Gromov fenti munkája rengeteg további eredményhez vezetett a szimplektikus invariánsok elméletében, mindegyik pszeudoholomorf görbéket használva alapnak. Ezen konstrukciók bonyolult komplex analitikus elveket és Fredholm-elméletet alkalmaznak. Nagyon fontos részét képezik napjaink szimplektikus topológiai és türörszimmetriai kutatásainak, és fontos perspektívát nyújtanak négy-sokaságok invariánsainak megértéséhez is.
választásra létezik térfogatmegőrző leképezés. Informálisan szólva, a szimplektikus teve nem tud átbújni a tű fokán. Gromov fenti munkája rengeteg további eredményhez vezetett a szimplektikus invariánsok elméletében, mindegyik pszeudoholomorf görbéket használva alapnak. Ezen konstrukciók bonyolult komplex analitikus elveket és Fredholm-elméletet alkalmaznak. Nagyon fontos részét képezik napjaink szimplektikus topológiai és türörszimmetriai kutatásainak, és fontos perspektívát nyújtanak négy-sokaságok invariánsainak megértéséhez is.
A momentumleképezésről további részletek [1]-ben találhatók, míg a pszeudoholomorf görbék elméletét [2] dolgozza fel.
Irodalomjegyzék
- [1] A. Cannas da Silva, Lectures on Symplectic Geometry, Lecture Notes in Mathematics, 1764, Springer-Verlag, Berlin, 2001. MR 1853077
[2] D. McDuff and D. Salamon, Introduction to Symplectic Topology, Oxford Mathematical Monographs, Oxford University Press, New York, 1995. MR 1373431
Tara S. Holm
- Tara S. Holm a Cornell Egyetem matematika professzora, és a Notices of the AMS külső munkatársa. Cikke a Simons Foundation támogatásával a 2016. decemberi számban jelent meg. Az Érintő a dolgozatot az AMS és a szerző engedélyével közli.
- A fordítást Stipsicz András készítette.
Tara S. Holm: What is....Symplectic Geometry? Notices Amer. Math. Soc. Vol. 63 Num. 11.(December 2016) 1252-1254 (The graduate student section) ©2016 American Mathematical Society, https://www.ams.org/publications/journals/notices/ 201611/rnoti-p1252.pdf.









