Az ukrán matematika egyik ékköve: Sarkovszkij tétele

1975-ben Li és Yorke amerikai matematikusok egy nagyon érdekes cikket közöltek Period three implies chaos címmel. Ebben a tanulmányban jelent meg először a káosz, mint matematikai fogalom. Miről is szólt az ő munkájuk? Tekintsünk egy folytonos függvényt, ami egy intervallumot, például a -et önmagába képezi, vagyis 0 és 1 közötti értékeket vehet föl. Vegyünk egy kiindulási számot, és értékeljük ki ott ezt a függvényt. Ekkor kapunk egy új számot. Most értékeljük ki a függvényünket ezen az új helyen, és ezt ismételgessük, magyarul szólva iteráljuk a függvényt. Kapunk tehát egy pontsorozatot, amit felfoghatunk úgy is, hogy az 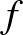függvény által meghatározott módon bolyongunk a intervallumban. A kérdés az, hogy hova juthatunk. Lehetnek olyan 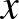számok, amelyekre 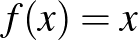(úgynevezett fixpont), és akkor végig egyhelyben toporgunk. 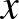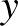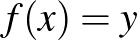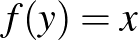Ha van két különböző és pont, hogy és , akkor világos, hogy két lépés után mindig visszatérünk az 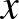pontba. Ezeket 2-periodikus pontoknak nevezzük. Hasonlóan definiálhatóak a 3, 4, …, 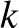-periodikus pontok is, amikor éppen 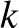lépés után érünk vissza először a kiindulási helyzetbe.

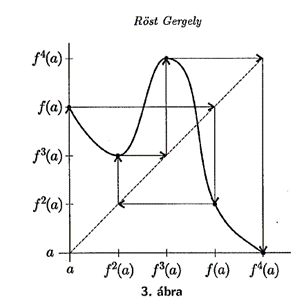
Li és Yorke egyik fontos eredménye a következő: ha egy függvénynek van 3-periodikus pontja, akkor tetszőleges 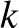-ra létezik 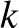-periodikus pontja is, vagyis végtelen sok periodikus pont van, és az összes lehetséges periódus szükségszerűen előfordul. Ez azért elég meghökkentően hangzik első hallásra. A cikkben persze más is van, érdemes elolvasni. Mindez olyan nagy érdeklődést váltott ki a matematikusok körében, hogy azóta több mint ötezer hivatkozást kapott, vagyis ennyi matematikai publikáció idézi Li és Yorke eredményeit.

Most jön a csavar: kiderült, hogy már egy évtizeddel korábban egy fiatal ukrán matematikus a fent említettnél sokkal többet bizonyított. Az illetőt úgy hívják, hogy Olekszandr Sarkovszkij, és 1964-ben publikálta eredményeit orosz nyelven, az Ukrajnszki Matematicski Zsurnal hasábjain. A szegedi Bolyai Intézet könyvtárában egyébként megtalálható ez a folyóirat, diákkoromban én is kikerestem a cikket és próbáltam megérteni.

Sarkovszkij az alábbit csinálta: rendezzük sorba a pozitív egész számokat, de ne a szokásos módon, hogy 1,2,3,…, hanem egy egészen speciális rendezés szerint:

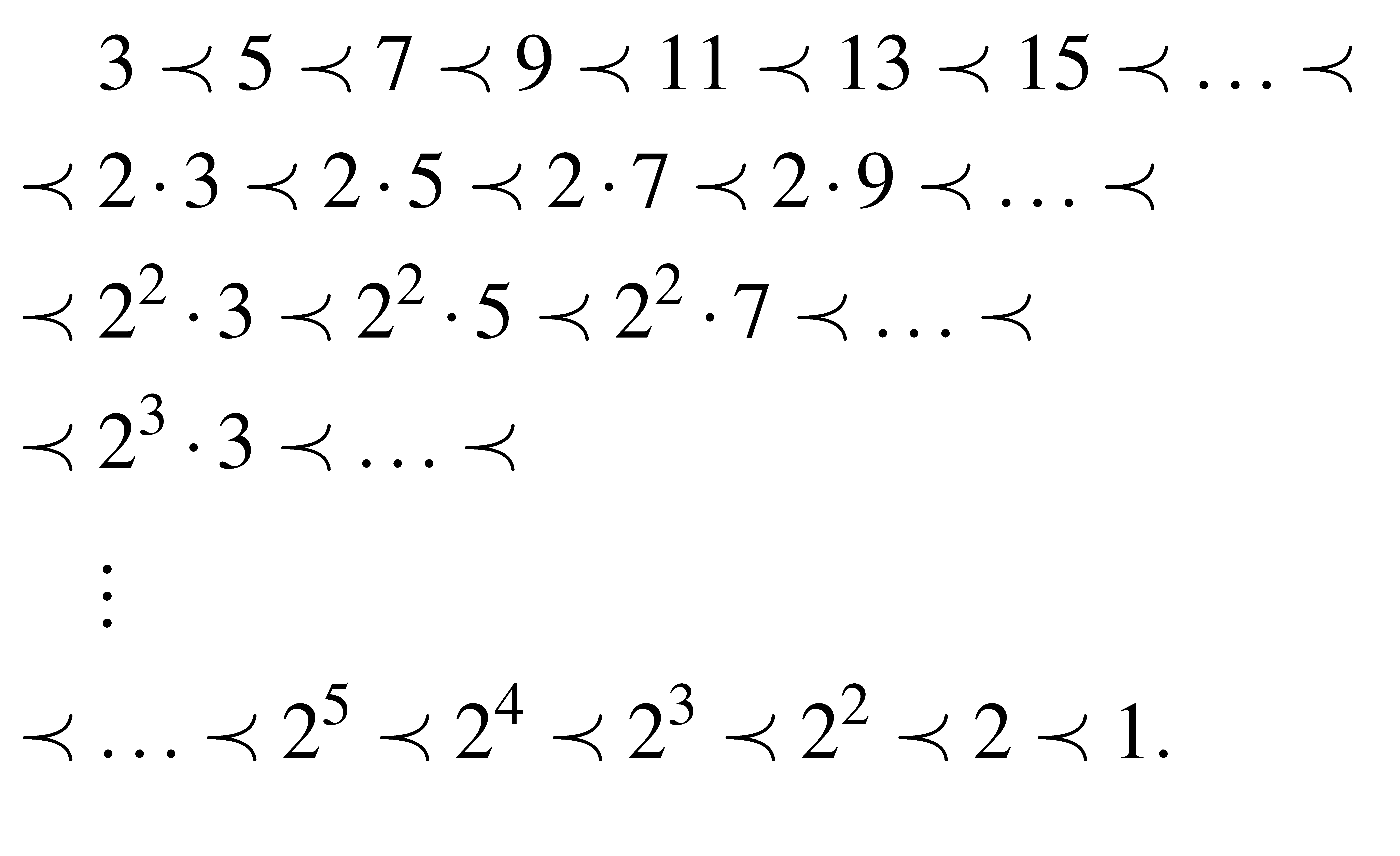
Vagyis kezdjük a páratlan számokkal növekvő sorrendben, majd jönnek a páratlan számok kétszeresei, aztán 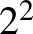-szorosai, 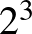-szorosai, és így tovább, végül a kettő-hatványok csökkenő sorrendben. Világos, hogy minden számot felsoroltunk, és az is, hogy bármely két számról könnyen el tudjuk dönteni, hogy melyik van előrébb. Sarkovszkij tétele azt állítja, hogy ha egy függvénynek van 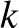-periodikus pontja, akkor van 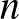-periodikus pontja is, h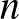a a 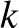után jön ebben a rendezésben. Például 8-periodikus pont létezéséből következik 4-periodikus és 2-periodikus pont létezése, 3-periodikus pont létezéséből következik az összes periódus (ez a speciális eset éppen Li–Yorke tétele), 5-periodikus pont létezéséből következik az összes periódus kivéve három, és így tovább.

Ez az egyik kedvenc matematikai tételem, egyetemista koromban írtam is róla egy esszét Pintér Lajos tanár úr analízis kurzusán, ami később a szegedi Polygon folyóiratban is megjelent (X. kötet, 1. szám, 2000), itt elolvasható a teljes bizonyításnak egy olyan elemi változata, ami akár középiskolás tudással is megérthető.

Sarkovszkij tétele tehát sokkal részletesebben feltárja a periodikus pontok közötti viszonyokat, az ukrán folyóiratban közölt cikke azonban annyira eltűnt a süllyesztőben, hogy a megjelenését követő tíz éves időszakból én egyetlen hivatkozást sem tudtam fellelni. A nemzetközi matematikus világ csak jóval Li és Yorke cikke után fedezte fel Sarkovszkijt, és kiderült, hogy a hatvanas években ő már egy egész sor szenzációs eredményt közölt, amiről addig szinte senki sem tudott. Így, ha nagy késéssel is, de végül megkapta a megérdemelt elismerést, és a diszkrét dinamikai rendszerek területén ma már nem létezhet tankönyv Sarkovszkij eredményeinek ismertetése nélkül.

A történet szereplői közül James Yorke 80 éves, a University of Maryland professzora, és még manapság is aktívan publikál új eredményeket. Tien-Yien Li 2020-ban, 75 éves korában elhunyt. Sarkovszkij 85 éves, de 2020-ban még publikált egy cikket. Kijevben született, egész életében ott dolgozott, és jelenleg is az orosz hadsereg által éppen ostromlott városban él.