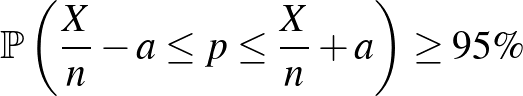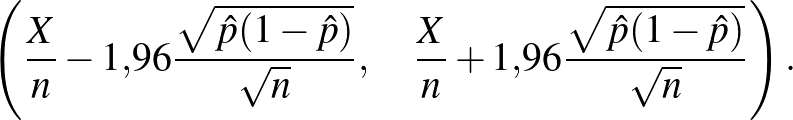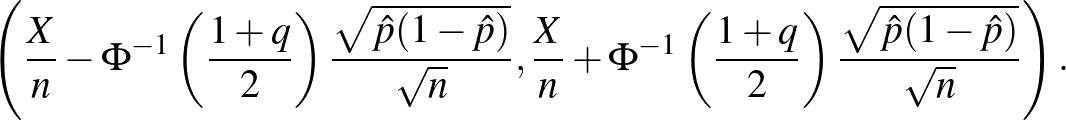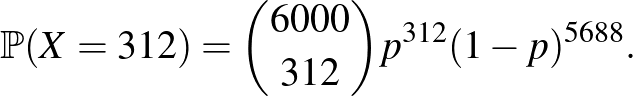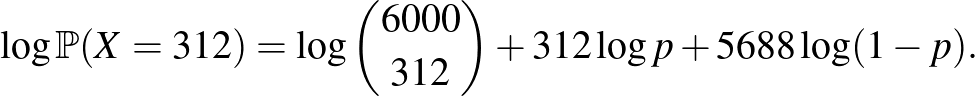Cikkünk második részében folytatjuk a betegek arányának becslésével kapcsolatos, gyakran használt valószínűségszámítási, statisztikai ismeretek összefoglalását annak a kérdésnek a kapcsán, hogy hány tesztet érdemes végezni, ha az arányt adott pontossággal szeretnénk megbecsülni egy véletlenszerűen választott minta alapján. A kiindulás a következő:
 Tegyük fel, hogy egy országban egy bizonyos betegségben szenvedők aránya
Tegyük fel, hogy egy országban egy bizonyos betegségben szenvedők aránya  , ennek értékét azonban nem ismerjük.
, ennek értékét azonban nem ismerjük.
 Kiválasztunk
Kiválasztunk  embert véletlenszerűen. Őket megvizsgálva,
embert véletlenszerűen. Őket megvizsgálva,  beteget találunk az
beteget találunk az 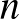 közül. Itt
közül. Itt 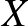 véletlen érték, tehát egy valószínűségi változó, míg
véletlen érték, tehát egy valószínűségi változó, míg 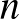 vagy adott, vagy általunk megválasztható.
vagy adott, vagy általunk megválasztható.

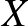 és
és 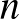 segítségével, pontosabban az
segítségével, pontosabban az 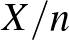 arány segítségével becsüljük
arány segítségével becsüljük  -t – kérdés, hogy mennyire megbízható a becslésünk, hiszen egyáltalán nem mindegy, hogy
-t – kérdés, hogy mennyire megbízható a becslésünk, hiszen egyáltalán nem mindegy, hogy 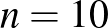 vagy
vagy 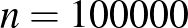 embert vizsgáltunk meg.
embert vizsgáltunk meg.
Az alábbi feltételezésekkel éltünk (bár, ahogyan az első rész [3] végén láttuk, ezek némelyike nagyon nehezen vagy egyáltalán nem érhető el a valóságban):
 a mintavételnél az embereket egymástól függetlenül választjuk (egy-egy ember többször is szerepelhet);
a mintavételnél az embereket egymástól függetlenül választjuk (egy-egy ember többször is szerepelhet);
 minden alkalommal mindenkit azonos valószínűséggel választunk;
minden alkalommal mindenkit azonos valószínűséggel választunk;
 a tesztek tökéletesen megbízhatók.
a tesztek tökéletesen megbízhatók.
Ezen feltételek mellett az első részben arra a kérdésre kerestük a választ, hogy adott pontosság eléréséhez hány vizsgálat elvégzésére van szükség. Ugyanakkor a tesztek számát gyakran nem mi választjuk meg, így az is jogos kérdés, hogy a tesztek adott számának és az eredményeknek az ismeretében hogyan fejezhetjük ki, hogy a betegek ismeretlen arányára kiszámított becslésben mennyire vagyunk biztosak, például hány tizedesjegy pontosságig vállalkoznánk  becslésére. Ha például
becslésére. Ha például 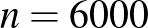 ember közül
ember közül 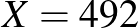 beteget találtunk, akkor
beteget találtunk, akkor  -nek az ötödik (vagyis a százezredekre vonatkozó) vagy annál későbbi tizedesjegyeiről teljesen megalapozatlan lenne bármit is állítani, viszont az első tizedesjegyről elég magabiztosan mondhatjuk, hogy 0, hiszen
-nek az ötödik (vagyis a százezredekre vonatkozó) vagy annál későbbi tizedesjegyeiről teljesen megalapozatlan lenne bármit is állítani, viszont az első tizedesjegyről elég magabiztosan mondhatjuk, hogy 0, hiszen 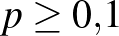 esetén a betegek számának várható értéke legalább 600, és annak valószínűsége, hogy ettől legalább 108 az eltérés, nem lehet túl nagy. A binomiális eloszlás képlete alapján ezt pontosan ki is számíthatjuk: annak valószínűsége, hogy
esetén a betegek számának várható értéke legalább 600, és annak valószínűsége, hogy ettől legalább 108 az eltérés, nem lehet túl nagy. A binomiális eloszlás képlete alapján ezt pontosan ki is számíthatjuk: annak valószínűsége, hogy 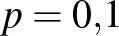 esetén pontosan 492 beteget találunk,
esetén pontosan 492 beteget találunk, 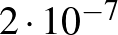 , nagyobb
, nagyobb  esetén még ennél is kisebb. Ezzel szemben például
esetén még ennél is kisebb. Ezzel szemben például 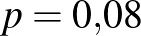 mellett a betegek számának várható értéke 480, és annak valószínűsége, hogy pontosan 492 beteget találunk, 1,6%. Vagyis a bekövetkezett esemény
mellett a betegek számának várható értéke 480, és annak valószínűsége, hogy pontosan 492 beteget találunk, 1,6%. Vagyis a bekövetkezett esemény 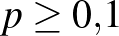 esetén nagyságrendekkel kevésbé valószínű, mint a
esetén nagyságrendekkel kevésbé valószínű, mint a 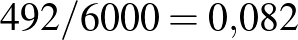 -höz jóval közelebbi
-höz jóval közelebbi  esetén. Ez erős érv amellett, hogy az első tizedesjegy 0. Ugyanakkor biztosat sosem állíthatunk egyik tizedesjegyről sem, hiszen tetszőleges 0 és
esetén. Ez erős érv amellett, hogy az első tizedesjegy 0. Ugyanakkor biztosat sosem állíthatunk egyik tizedesjegyről sem, hiszen tetszőleges 0 és 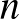 közötti érték (a határokat is beleértve) előfordulhat bármely
közötti érték (a határokat is beleértve) előfordulhat bármely 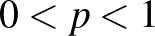 esetén. Célunk olyan állítások megfogalmazása, hogy például ha
esetén. Célunk olyan állítások megfogalmazása, hogy például ha 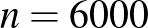 ember közül
ember közül 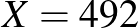 volt beteg, akkor a betegek valódi
volt beteg, akkor a betegek valódi  aránya 7% és 9% közé esik, és ebben 95%-ban biztosak vagyunk. Ez a megfogalmazás így még nem pontos, nem mondtuk meg, hogy mit jelent nagy valószínűséggel biztosnak lenni valamiben. Ennek egy lehetséges értelmezéseként mutatjuk be a konfidenciaintervallum fogalmát, amely a példaként említett 492-es betegszámhoz tartozó olyan intervallum, amelyben a keresett
aránya 7% és 9% közé esik, és ebben 95%-ban biztosak vagyunk. Ez a megfogalmazás így még nem pontos, nem mondtuk meg, hogy mit jelent nagy valószínűséggel biztosnak lenni valamiben. Ennek egy lehetséges értelmezéseként mutatjuk be a konfidenciaintervallum fogalmát, amely a példaként említett 492-es betegszámhoz tartozó olyan intervallum, amelyben a keresett  érték adott, általunk választott valószínűséggel benne van. A cikkben ezt mutatjuk be először, alkalmazva a magyar COVID-19 járványhoz kapcsolódó 2020. májusi reprezentatív felmérésre, ahol
érték adott, általunk választott valószínűséggel benne van. A cikkben ezt mutatjuk be először, alkalmazva a magyar COVID-19 járványhoz kapcsolódó 2020. májusi reprezentatív felmérésre, ahol 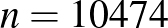 vizsgált ember közül
vizsgált ember közül 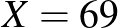 olyat találtak, aki már átesett a betegségen [8]. Ezután rátérünk a maximum-likelihood módszer ismertetésére, amely magát a becslési módszert, vagyis a
olyat találtak, aki már átesett a betegségen [8]. Ezután rátérünk a maximum-likelihood módszer ismertetésére, amely magát a becslési módszert, vagyis a  valószínűségnek az
valószínűségnek az 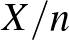 relatív gyakorisággal (a betegek arányával) való becslését támasztja alá. Ez az eljárás arra a kérdésre ad választ, hogy mely
relatív gyakorisággal (a betegek arányával) való becslését támasztja alá. Ez az eljárás arra a kérdésre ad választ, hogy mely  érték esetében a legvalószínűbb, hogy pont 492 beteget találunk a 6000 ember között. A binomiális eloszlás esetében kiderül, hogy éppen
érték esetében a legvalószínűbb, hogy pont 492 beteget találunk a 6000 ember között. A binomiális eloszlás esetében kiderül, hogy éppen 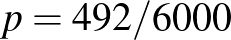 esetén. Persze ezen kívül is számtalan természetes érvet lehet felhozni a relatív gyakorisággal való becslés mellett (például hogy torzítatlan [4], vagyis
esetén. Persze ezen kívül is számtalan természetes érvet lehet felhozni a relatív gyakorisággal való becslés mellett (például hogy torzítatlan [4], vagyis 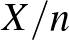 várható értéke megegyezik a becsülni kívánt
várható értéke megegyezik a becsülni kívánt  -vel), de van ellenérv is: ha egyetlen beteget sem találunk, akkor a becslésünk mindig 0 lesz, holott egészen mást jelent
-vel), de van ellenérv is: ha egyetlen beteget sem találunk, akkor a becslésünk mindig 0 lesz, holott egészen mást jelent  -re nézve, ha
-re nézve, ha 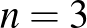 , 10, 100, 1000,
, 10, 100, 1000, 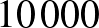 vagy
vagy 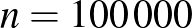 embert tesztelve nem találunk egyetlen beteget sem. A relatív gyakoriság ezt a különbséget nem veszi észre. Többek között ezt küszöböli ki a Bayes-becslés módszere, amelyre most nem térünk ki, de amiből például
embert tesztelve nem találunk egyetlen beteget sem. A relatív gyakoriság ezt a különbséget nem veszi észre. Többek között ezt küszöböli ki a Bayes-becslés módszere, amelyre most nem térünk ki, de amiből például 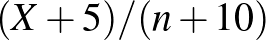 alakú becslés kapható (megfelelő előzetes feltételezés mellett), amire már
alakú becslés kapható (megfelelő előzetes feltételezés mellett), amire már 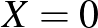 esetén is igaz, hogy minél nagyobb
esetén is igaz, hogy minél nagyobb 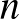 , annál kisebb a becslés. (A Bayes-becslésnek többek között Bolla és Krámli könyvében [4] lehet utánaolvasni.) Vagyis a relatív gyakoriság nem az egyetlen és nem minden szempontból a legjobb lehetőség, szólnak érvek mellette és ellene is. A cikkben egy mellette szóló módszert, a maximumlikelihood-becslést mutatjuk be, aminek az alkalmazási lehetőségei természetesen jóval szélesebbek, mint konkrétan a
, annál kisebb a becslés. (A Bayes-becslésnek többek között Bolla és Krámli könyvében [4] lehet utánaolvasni.) Vagyis a relatív gyakoriság nem az egyetlen és nem minden szempontból a legjobb lehetőség, szólnak érvek mellette és ellene is. A cikkben egy mellette szóló módszert, a maximumlikelihood-becslést mutatjuk be, aminek az alkalmazási lehetőségei természetesen jóval szélesebbek, mint konkrétan a  becslése a mi esetünkben [4,7].
becslése a mi esetünkben [4,7].
Cikkünkben a valószínűségszámítás és az analízis alapvető eszközeinek (binomiális eloszlás, deriválás), illetve az első részben szerepelt néhány állításnak a felhasználásával ismertetjük az említett fogalmakat azok számára, akik ezekkel az egyetemi statisztika órákon is gyakran szereplő módszerekkel nem találkoztak, vagy szeretnék az ezzel kapcsolatos ismereteiket felidézni.
1. Konfidenciaintervallum a betegek arányára
Célunk tehát elsőként az, hogy az 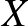 (a talált betegek száma) és az
(a talált betegek száma) és az 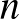 (a vizsgált emberek száma) ismeretében a
(a vizsgált emberek száma) ismeretében a  -re olyan becslést adjunk, amelyből a kapott érték pontossága vagy bizonytalansága is kiderül. Ezt a következő módon szeretnénk megvalósítani:
-re olyan becslést adjunk, amelyből a kapott érték pontossága vagy bizonytalansága is kiderül. Ezt a következő módon szeretnénk megvalósítani:
 az elvégzett vizsgálatok és a talált betegek száma (vagyis
az elvégzett vizsgálatok és a talált betegek száma (vagyis 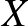 és
és 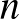 ) alapján mondunk határokat
) alapján mondunk határokat  -re, például hogy 7% és 9% közé esik;
-re, például hogy 7% és 9% közé esik;
 megadjuk azt is, hogy mennyire vagyunk biztosak abban, hogy
megadjuk azt is, hogy mennyire vagyunk biztosak abban, hogy  a megadott határok között lehet, és minél megbízhatóbb becslést szeretnénk;
a megadott határok között lehet, és minél megbízhatóbb becslést szeretnénk;
 az intervallumot megpróbáljuk a lehető legrövidebbre választani, hogy minél informatívabb legyen az állításunk: az, hogy
az intervallumot megpróbáljuk a lehető legrövidebbre választani, hogy minél informatívabb legyen az állításunk: az, hogy  értéke 7% és 9% közé esik, sokkal többet mond, mint például az, hogy
értéke 7% és 9% közé esik, sokkal többet mond, mint például az, hogy  értéke 5% és 25% közé esik.
értéke 5% és 25% közé esik.
Vegyük észre, hogy a második és a harmadik szempont egymással szembe megy. Csak a második feltételt nagyon könnyű lenne teljesíteni: a ![$[0,1]$](/images/stories/latexuj/2020-08/2020-08-backhausagnesmennyitteszteljunk2/img24.png) intervallum egészen biztosan tartalmazza a betegek valódi arányát, és ha ezzel megelégednénk, még a tesztelés költségét is megtakaríthatnánk. Azonban épp ez az, amit a harmadik szemponttal kizárunk: minél rövidebb intervallumot szeretnénk, ami azonban még elég tág ahhoz, hogy nagy megbízhatósággal tartalmazza
intervallum egészen biztosan tartalmazza a betegek valódi arányát, és ha ezzel megelégednénk, még a tesztelés költségét is megtakaríthatnánk. Azonban épp ez az, amit a harmadik szemponttal kizárunk: minél rövidebb intervallumot szeretnénk, ami azonban még elég tág ahhoz, hogy nagy megbízhatósággal tartalmazza  -t.
-t.
Kicsit másképpen fogalmazva próbálhatjuk pontosítani a célt: olyan intervallumot szeretnénk, ami nagy valószínűséggel, például 95% valószínűséggel tartalmazza  -t. Azt azonban fontos tisztázni, hogy mit jelent itt a valószínűség: hiszen úgy gondolkoztunk, hogy a
-t. Azt azonban fontos tisztázni, hogy mit jelent itt a valószínűség: hiszen úgy gondolkoztunk, hogy a  , vagyis a betegek valódi aránya ugyan számunkra ismeretlen, de nem véletlen paraméter. Az tehát nem tűnik jó értelmezésnek, hogy az intervallum határai rögzítettek, amibe egy véletlenül kisorsolt
, vagyis a betegek valódi aránya ugyan számunkra ismeretlen, de nem véletlen paraméter. Az tehát nem tűnik jó értelmezésnek, hogy az intervallum határai rögzítettek, amibe egy véletlenül kisorsolt  vagy beleesik, vagy sem. Azonban, ha például
vagy beleesik, vagy sem. Azonban, ha például 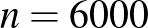 vizsgált lakos közül
vizsgált lakos közül 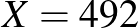 beteg, akkor nyilvánvalóan egészen más intervallum lesz jó, mint ha például 4328 beteget találtunk volna. Így az általunk meghatározott intervallum határai függnek
beteg, akkor nyilvánvalóan egészen más intervallum lesz jó, mint ha például 4328 beteget találtunk volna. Így az általunk meghatározott intervallum határai függnek 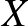 -től, a talált betegek számától, ez pedig a véletlen mintavételünktől függ. Ezért az intervallum maga lesz az, amit véletlenszerűen adunk meg – a feltétel pedig az, hogy minden
-től, a talált betegek számától, ez pedig a véletlen mintavételünktől függ. Ezért az intervallum maga lesz az, amit véletlenszerűen adunk meg – a feltétel pedig az, hogy minden  -re teljesüljön, hogy
-re teljesüljön, hogy  ebbe a véletlen intervallumba essen, kellőképpen nagy valószínűséggel. Ezt nevezzük konfidenciaintervallumnak. Megjegyezzük, hogy a „minden
ebbe a véletlen intervallumba essen, kellőképpen nagy valószínűséggel. Ezt nevezzük konfidenciaintervallumnak. Megjegyezzük, hogy a „minden  -re teljesüljön” feltétel értelmezéséhez körültekintőnek kell lennünk. Ugyanis
-re teljesüljön” feltétel értelmezéséhez körültekintőnek kell lennünk. Ugyanis  különböző értékeire maga a binomiális eloszlás is megváltozik, tehát az adott intervallumba kerülés valószínűsége is más lesz, amint alább hamarosan látni fogjuk. A konfidenciaintervallumot meghatározó nagy valószínűségnek egy szokásos választása
különböző értékeire maga a binomiális eloszlás is megváltozik, tehát az adott intervallumba kerülés valószínűsége is más lesz, amint alább hamarosan látni fogjuk. A konfidenciaintervallumot meghatározó nagy valószínűségnek egy szokásos választása 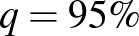 , ami egy előre rögzített érték, és bármi is a betegek valódi aránya vagy az általunk megtalált betegek száma, az ismeretlen
, ami egy előre rögzített érték, és bármi is a betegek valódi aránya vagy az általunk megtalált betegek száma, az ismeretlen  legalább ennyi valószínűséggel az általunk megadott határok közé esik. A
legalább ennyi valószínűséggel az általunk megadott határok közé esik. A 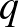 értékét nevezik a konfidenciaintervallum megbízhatósági szintjének, ezt mindig előzetesen adjuk meg.
értékét nevezik a konfidenciaintervallum megbízhatósági szintjének, ezt mindig előzetesen adjuk meg.
Most már tehát tudjuk, hogy milyen intervallumot szeretnénk, kérdés, hogy hogyan készítsük el. Bár nem minden esetben ez a legjobb választás (ahogy azt az 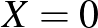 példán láttuk), abból indulunk ki, hogy
példán láttuk), abból indulunk ki, hogy  -t az
-t az 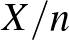 relatív gyakorisággal becsüljük, és ez lesz a konfidenciaintervallum közepe. A nehezebb feladat az, hogy mi legyen a konfidenciaintervallum hossza. Ehhez olyan
relatív gyakorisággal becsüljük, és ez lesz a konfidenciaintervallum közepe. A nehezebb feladat az, hogy mi legyen a konfidenciaintervallum hossza. Ehhez olyan 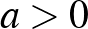 számot kell keresnünk, amelyre az
számot kell keresnünk, amelyre az 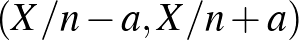 intervallum legalább
intervallum legalább 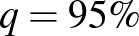 valószínűséggel tartalmazza
valószínűséggel tartalmazza  -t (a megbízhatósági szintet a szokásos értéknek választva). Vagyis az kellene, hogy minden
-t (a megbízhatósági szintet a szokásos értéknek választva). Vagyis az kellene, hogy minden 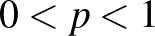 -re
-re
teljesüljön. A betegek valódi arányáról tehát nincs semmilyen előzetes feltételezésünk, olyan módszert keresünk, ami minden lehetséges  -re ebből a szempontból megfelelően működik. Fontos hangsúlyoznunk, hogy
-re ebből a szempontból megfelelően működik. Fontos hangsúlyoznunk, hogy 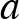 értéke az
értéke az 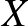 -től, a talált betegek számától függni fog,
-től, a talált betegek számától függni fog,  értékét viszont nem használhatjuk fel a kiszámításához, hiszen éppen ezt akarjuk megbecsülni. A megbízhatósági szint, amit most szokásos módon
értékét viszont nem használhatjuk fel a kiszámításához, hiszen éppen ezt akarjuk megbecsülni. A megbízhatósági szint, amit most szokásos módon 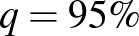 -nak választottunk, előre adott érték, de ennek is van hatása
-nak választottunk, előre adott érték, de ennek is van hatása 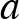 -ra: minél nagyobb a
-ra: minél nagyobb a 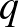 , annál nagyobb lesz
, annál nagyobb lesz 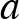 is – miközben persze arra is figyelünk, hogy
is – miközben persze arra is figyelünk, hogy 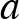 a megadott feltételek mellett a lehető legkisebb legyen, hogy minél informatívabb legyen az állításunk.
a megadott feltételek mellett a lehető legkisebb legyen, hogy minél informatívabb legyen az állításunk.
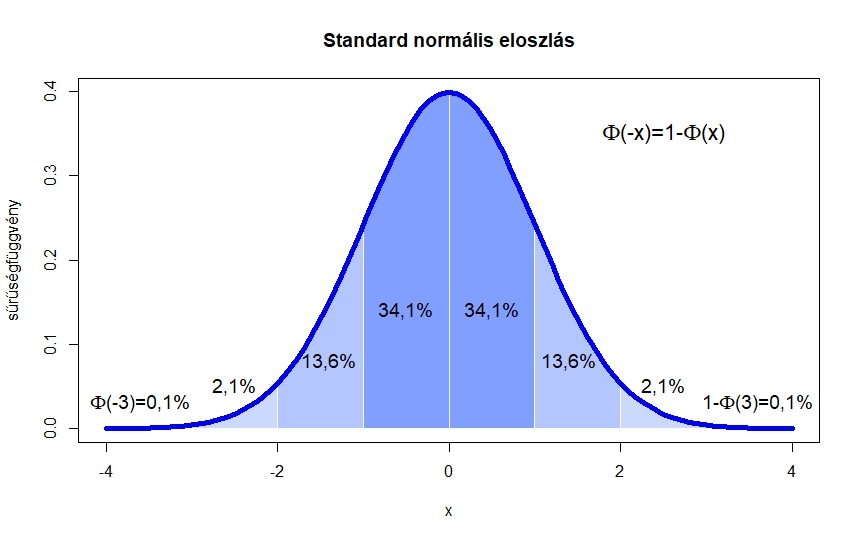
1. ábra. Az 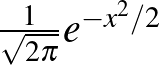 függvény és az alatta lévő területek
függvény és az alatta lévő területek
Ahhoz, hogy ezt az 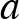 -t megtaláljuk, az (1) egyenlőtlenség bal oldalán álló kifejezést kellene kiszámítanunk. Cikkünk első részében ezt lényegében meg is tettük [3]. Ha ugyanis olyan átrendezést végzünk, hogy a feltétel az
-t megtaláljuk, az (1) egyenlőtlenség bal oldalán álló kifejezést kellene kiszámítanunk. Cikkünk első részében ezt lényegében meg is tettük [3]. Ha ugyanis olyan átrendezést végzünk, hogy a feltétel az 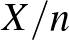 -nek a
-nek a  -től vett távolságára vonatkozzon, ehhez jutunk:
-től vett távolságára vonatkozzon, ehhez jutunk:
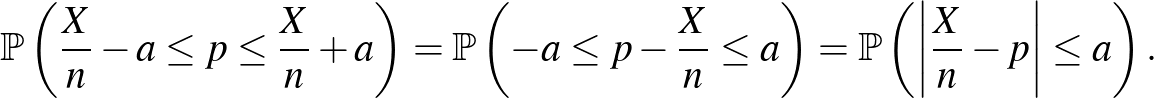
A cikk első részében pedig a de Moivre–Laplace-tételt az 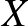 binomiális eloszlású valószínűségi változóra alkalmazva azt láttuk, hogy a fenti valószínűség közelíthető a standard normális eloszlásfüggvény, a
binomiális eloszlású valószínűségi változóra alkalmazva azt láttuk, hogy a fenti valószínűség közelíthető a standard normális eloszlásfüggvény, a  függvény segítségével. Pontosabban, az első rész (6) egyenletében az ott megadott 0,01 helyébe a most keresett
függvény segítségével. Pontosabban, az első rész (6) egyenletében az ott megadott 0,01 helyébe a most keresett  -t írva:
-t írva:
2. ábra. A standard normális eloszlásfüggvény, azaz 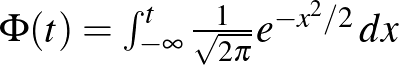 és
és 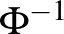
Itt a 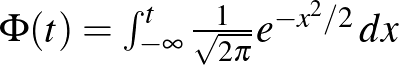 függvény egy
függvény egy 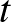 valós számhoz az 1. ábrán a
valós számhoz az 1. ábrán a 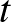 -től balra eső, függvény alatti területet rendelte hozzá (a teljes görbe alatti terület 1). Magát a
-től balra eső, függvény alatti területet rendelte hozzá (a teljes görbe alatti terület 1). Magát a  függvényt a 2. ábra bal oldalán láthatjuk. A közelítés azonban természetesen csak elég nagy mintaelemszám, pontosabban az
függvényt a 2. ábra bal oldalán láthatjuk. A közelítés azonban természetesen csak elég nagy mintaelemszám, pontosabban az 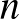 és a
és a  megfelelő viszonya esetén érvényes, ezt az
megfelelő viszonya esetén érvényes, ezt az 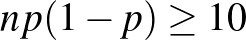 feltétellel szokták például kifejezni [10]. Ha viszont ez teljesül, akkor az (1) egyenlőtlenség feltétele alapján olyan
feltétellel szokták például kifejezni [10]. Ha viszont ez teljesül, akkor az (1) egyenlőtlenség feltétele alapján olyan 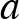 számot keresünk, amelyre
számot keresünk, amelyre
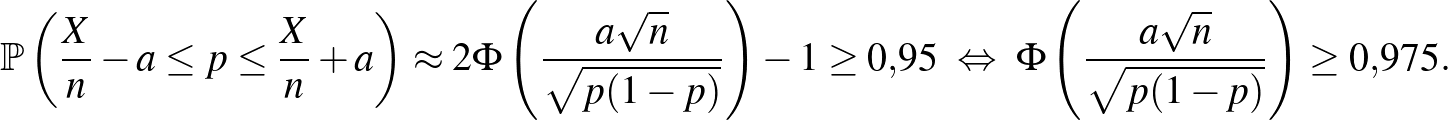
Ennek megoldásához a 0,975-nek a 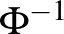 inverz függvénynél vett értékét kell meghatároznunk. Azt a legkisebb
inverz függvénynél vett értékét kell meghatároznunk. Azt a legkisebb 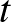 számot keressük tehát, amire
számot keressük tehát, amire 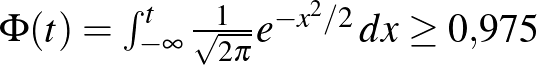 , vagyis amitől balra legalább 0,975 terület esik az 1. ábrán. Mivel
, vagyis amitől balra legalább 0,975 terület esik az 1. ábrán. Mivel 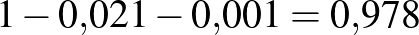 , ez a szám kettőnél kicsit kisebb kell, hogy legyen. Számítógéppel számolva
, ez a szám kettőnél kicsit kisebb kell, hogy legyen. Számítógéppel számolva 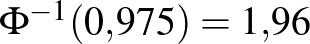 adódik, ezt a 2. ábra jobb oldali részéről is leolvashatjuk, ahol a
adódik, ezt a 2. ábra jobb oldali részéről is leolvashatjuk, ahol a  inverz függvényt ábrázoltuk. Vagyis a keresett
inverz függvényt ábrázoltuk. Vagyis a keresett  számra az alábbi feltételt kapjuk:
számra az alábbi feltételt kapjuk:
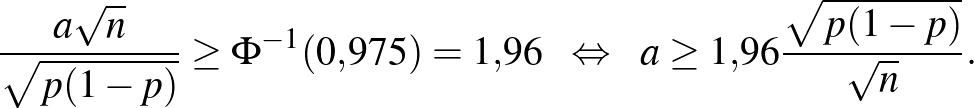
Ezzel azonban nem vagyunk kész. Az, hogy egy egyenlőtlenséget kaptunk, holott csak egy szám kellene, nem jelent gondot, hiszen 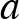 -t minél kisebbnek szeretnénk választani. A gond az, hogy a jobb oldalon álló kifejezésben nem csak
-t minél kisebbnek szeretnénk választani. A gond az, hogy a jobb oldalon álló kifejezésben nem csak 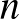 , a vizsgált emberek száma szerepel, hanem
, a vizsgált emberek száma szerepel, hanem  is, ami a betegek valódi aránya. Ez viszont éppen a keresett, ismeretlen érték, amire a konfidenciaintervallumot adjuk. Ezért a becslésben ez nem szerepelhet, azt az általunk rendelkezésre álló mennyiségek alapján kell felépítenünk. Egy lehetséges megoldás a
is, ami a betegek valódi aránya. Ez viszont éppen a keresett, ismeretlen érték, amire a konfidenciaintervallumot adjuk. Ezért a becslésben ez nem szerepelhet, azt az általunk rendelkezésre álló mennyiségek alapján kell felépítenünk. Egy lehetséges megoldás a 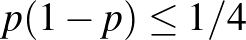 egyenlőtlenség alkalmazása, ami sajnos indokolatlanul hosszú intervallumot (túl nagy
egyenlőtlenség alkalmazása, ami sajnos indokolatlanul hosszú intervallumot (túl nagy 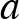 értéket) eredményezhet. Alternatívaként alkalmazhatjuk a már egyszer bevált stratégiát, nevezetesen azt, amikor a konfidenciaintervallum közepének a
értéket) eredményezhet. Alternatívaként alkalmazhatjuk a már egyszer bevált stratégiát, nevezetesen azt, amikor a konfidenciaintervallum közepének a  -re vonatkozó becslésünket, vagyis a betegek
-re vonatkozó becslésünket, vagyis a betegek 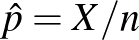 relatív gyakoriságát választottuk.
relatív gyakoriságát választottuk.
Ezt alkalmazva tehát közelítőleg érvényes gondolatmenetünk van (amely precízzé tehető a statisztika megfelelő tételeinek segítségével) arra, hogy ha 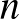 megkérdezett közül
megkérdezett közül 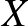 beteget találunk, akkor az alábbi intervallum 95%-os megbízhatósági szintű konfidenciaintervallum
beteget találunk, akkor az alábbi intervallum 95%-os megbízhatósági szintű konfidenciaintervallum  -re, vagyis az alább megadott véletlen határok legalább 95% valószínűséggel közrefogják
-re, vagyis az alább megadott véletlen határok legalább 95% valószínűséggel közrefogják  -t, bármi is legyen annak értéke:
-t, bármi is legyen annak értéke:
A korábban említett példában, ha 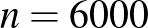 ember közül
ember közül 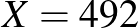 beteg, akkor tehát
beteg, akkor tehát 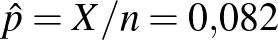 , és a konfidenciaintervallum:
, és a konfidenciaintervallum:
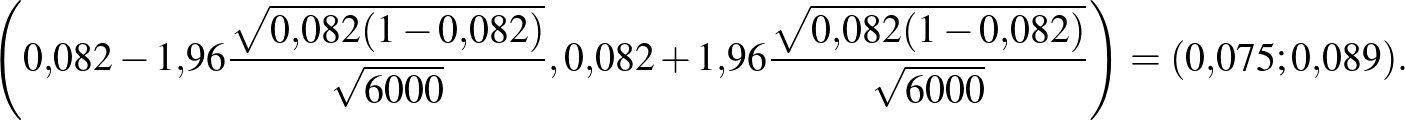
Tehát ebben az esetben azt mondhatjuk, hogy a betegek valódi aránya 7,5% és 8,9% közé esik, és ezt egy 95%-os megbízhatósági szintű konfidenciaintervallum alapján állíthatjuk. Ugyanerre az intervallumra az alábbi jelölést is használni fogjuk: 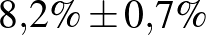 . Ez tehát nem azt jelenti, hogy a
. Ez tehát nem azt jelenti, hogy a  biztosan ebbe az intervallumba esik, ha például a valódi
biztosan ebbe az intervallumba esik, ha például a valódi 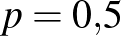 , akkor is előfordulhat, hogy úgy alakul a véletlen mintavételezés, hogy
, akkor is előfordulhat, hogy úgy alakul a véletlen mintavételezés, hogy 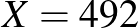 beteget találunk csak a várt 3000 helyett, és
beteget találunk csak a várt 3000 helyett, és  a legkevésbé sem esik bele az általunk megadott
a legkevésbé sem esik bele az általunk megadott 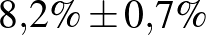 intervallumba – de az ilyen típusú tévedések valószínűsége összesen sem több 5%-nál.
intervallumba – de az ilyen típusú tévedések valószínűsége összesen sem több 5%-nál.
A fenti képlettel a H-UNCOVER 2020. május 1-16-ig végzett vizsgálata alapján azt mondhatjuk, hogy a SARS-CoV-2 vírussal korábban megfertőződött (aktívan beteg vagy már meggyógyult) emberek aránya Magyarországon 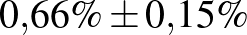 lehetett ebben az időszakban (a 14 éven felüli, nem intézményben lakó emberek között). Itt ugyanis
lehetett ebben az időszakban (a 14 éven felüli, nem intézményben lakó emberek között). Itt ugyanis 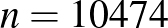 teszt alapján
teszt alapján 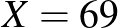 embernél mutatták ki, hogy átestek ezen a betegségen [8]. Ugyanakkor ne felejtsük el, hogy végig a legideálisabb esettel számoltunk, és azt sem vizsgáltuk, hogy a feltehetően kicsi
embernél mutatták ki, hogy átestek ezen a betegségen [8]. Ugyanakkor ne felejtsük el, hogy végig a legideálisabb esettel számoltunk, és azt sem vizsgáltuk, hogy a feltehetően kicsi  miatt nem romlik-e el a közelítés (bár azt megállapíthatjuk, hogy ha
miatt nem romlik-e el a közelítés (bár azt megállapíthatjuk, hogy ha 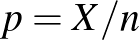 -t helyettesítünk, akkor az
-t helyettesítünk, akkor az 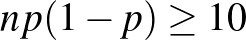 feltétel teljesül), ezért az intervallum hosszát inkább csak alsó becslésnek tekinthetjük. Ugyanebben a vizsgálatban
feltétel teljesül), ezért az intervallum hosszát inkább csak alsó becslésnek tekinthetjük. Ugyanebben a vizsgálatban 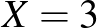 aktív beteget találtak az
aktív beteget találtak az 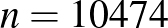 vizsgált ember között. Ekkor azonban az
vizsgált ember között. Ekkor azonban az 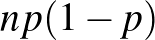 érték a becsült
érték a becsült  -vel számolva 3-nál is kevesebb, a feltételünk egyáltalán nem teljesül, a módszerünk közelítésből adódó hibája annyira nagy, hogy jobb, ha nem alkalmazzuk a képletünket konfidenciaintervallum készítésére. Ebben a konkrét esetben közvetlenül a binomiális eloszlást használva (a korábbi számoláshoz hasonlóan) azonban észrevehetjük, hogy ha például
-vel számolva 3-nál is kevesebb, a feltételünk egyáltalán nem teljesül, a módszerünk közelítésből adódó hibája annyira nagy, hogy jobb, ha nem alkalmazzuk a képletünket konfidenciaintervallum készítésére. Ebben a konkrét esetben közvetlenül a binomiális eloszlást használva (a korábbi számoláshoz hasonlóan) azonban észrevehetjük, hogy ha például 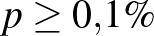 , akkor annak valószínűsége, hogy legfeljebb 3 beteget találunk ennyi vizsgált ember között, 0,0067. Vagyis azt mondhatjuk, hogy 1 ezreléknél nem lehetett lényegesen több az aktív betegek aránya (a relatív gyakoriság 0,28 ezrelék), de a nagyságrendről sokkal pontosabbat nem állíthatunk, a konfidenciaintervallumhoz pedig ennél alaposabb vizsgálatra lenne szükség.
, akkor annak valószínűsége, hogy legfeljebb 3 beteget találunk ennyi vizsgált ember között, 0,0067. Vagyis azt mondhatjuk, hogy 1 ezreléknél nem lehetett lényegesen több az aktív betegek aránya (a relatív gyakoriság 0,28 ezrelék), de a nagyságrendről sokkal pontosabbat nem állíthatunk, a konfidenciaintervallumhoz pedig ennél alaposabb vizsgálatra lenne szükség.
2. Mitől függhet a konfidenciaintervallum hossza?
Most már tehát van egy képletünk a konfidenciaintervallumra, ezt vizsgáljuk meg részletesebben. Elsőként szögezzük le, hogy a becslések és közelítések miatt ennek a módszernek számos hátulütője lehet, hiszen nem adtunk meg pontosan, hogy mekkora a hiba a normális eloszlással való közelítésnél (erről szól a Berry–Esséen-tétel, [6]), és azt sem, hogy mekkorát hibázunk, amikor a valódi  -t a becsült értékkel helyettesítettük az utolsó lépésben. Sőt, semmi nem zárja ki, hogy csak nagyon kevés, esetleg 0 beteget találunk, és ilyenkor a bal végpont negatív lesz, márpedig nem túl szerencsés egy költséges vizsgálat végén megállapítani, hogy a valószínűség –2% és 2% közé esik – az állítás egy részéhez ugyanis egyetlen mérésre sem lett volna szükség. Erre nem térünk ki, de a fentinél természetesen sokkal kifinomultabb módszerek is használhatók a konfidenciaintervallum építésére [1,9], amelyek ezeket a hátrányokat legalább részben kiküszöbölik. Ugyanakkor már a fenti képlet alapján is megfogalmazhatjuk a konfidenciaintervallumnak néhány olyan tulajdonságát, amelyek lényegében módszertől függetlenül érvényesek. Ehhez először tekintsük a táblázatot, amely néhány különböző
-t a becsült értékkel helyettesítettük az utolsó lépésben. Sőt, semmi nem zárja ki, hogy csak nagyon kevés, esetleg 0 beteget találunk, és ilyenkor a bal végpont negatív lesz, márpedig nem túl szerencsés egy költséges vizsgálat végén megállapítani, hogy a valószínűség –2% és 2% közé esik – az állítás egy részéhez ugyanis egyetlen mérésre sem lett volna szükség. Erre nem térünk ki, de a fentinél természetesen sokkal kifinomultabb módszerek is használhatók a konfidenciaintervallum építésére [1,9], amelyek ezeket a hátrányokat legalább részben kiküszöbölik. Ugyanakkor már a fenti képlet alapján is megfogalmazhatjuk a konfidenciaintervallumnak néhány olyan tulajdonságát, amelyek lényegében módszertől függetlenül érvényesek. Ehhez először tekintsük a táblázatot, amely néhány különböző 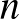 és
és 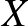 esetén ad 95%-os megbízhatósági szintű konfidenciaintervallumot (az intervallum helyett áttérünk a
esetén ad 95%-os megbízhatósági szintű konfidenciaintervallumot (az intervallum helyett áttérünk a  -os jelölésre, vagyis
-os jelölésre, vagyis 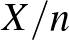 -t és az intervallum hosszának felét adjuk meg, amelyet korábban
-t és az intervallum hosszának felét adjuk meg, amelyet korábban 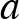 -val jelöltünk).
-val jelöltünk).
tesztek száma (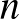 ) ) |
betegek száma (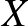 ) ) |
konfidenciaintervallum |
| 100 | 10 | 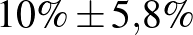 |
| 100 | 30 | 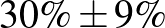 |
| 100 | 50 | 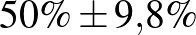 |
| 1000 | 100 | 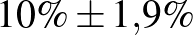 |
| 1000 | 300 | 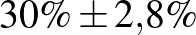 |
| 1000 | 500 | 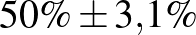 |
| 10000 | 1000 | 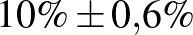 |
| 10000 | 3000 | 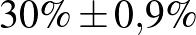 |
| 10000 | 5000 | 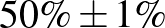 |
| 100000 | 10000 | 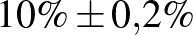 |
| 100000 | 30000 | 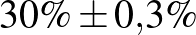 |
| 100000 | 50000 | 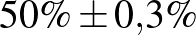 |
| 10474 | 69 | 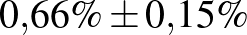 |
Táblázat. 95%-os megbízhatósági szintű konfidenciaintervallum az elvégzett tesztek és a megtalált betegek számának függvényében. Az utolsó sor a H-UNCOVER 2020. május 1–16-i reprezentatív SARS-CoV-2 átfertőzöttségi felmérésének adata [8]
Ebből és a (2) képletből az alábbi következtetéseket vonhatjuk le.
Mintaelemszám. A betegek arányát rögzítve (a táblázatban például a vonalak alatti sorokat tekintve, az utolsó kivételével) a konfidenciaintervallum hossza közelítőleg fordítottan arányos a mintaelemszám gyökével. Tehát feleolyan hosszú intervallumhoz négyszerannyi, tizedolyan hosszú intervallumhoz százszorannyi teszt szükséges. Ez összhangban van a cikkünk első részében tett megállapításokkal, ott ezt úgy mondtuk, hogy a pontosságot növelve négyzetesen növekszik a szükséges tesztek száma.
Ritkaság. Minél közelebb van a betegek aránya a 0-hoz vagy az 1-hez (legalábbis a mintában), vagyis minél ritkább a betegség vagy épp a nem-betegség, annál rövidebb a konfidenciaintervallum. Azonban, ahogy szintén az első részben is láttuk, ha ezt a hosszt a  -hez viszonyítjuk, vagyis azt kérdezzük, hogy
-hez viszonyítjuk, vagyis azt kérdezzük, hogy  -nek hányszorosa a hiba, akkor már egész más válasz adódik. A táblázatban a „legritkább eset” az utolsó sor, amely a H-UNCOVER felmérés adatait tartalmazza [8], ahol SARS-CoV-2 koronavírussal való, korábbi vagy aktív fertőzöttséget mutatták ki (tehát a már gyógyultak is számítanak, amíg a szervezetükben megtalálható a vírussal szembeni ellenanyag). Itt a konfidenciaintervallum
-nek hányszorosa a hiba, akkor már egész más válasz adódik. A táblázatban a „legritkább eset” az utolsó sor, amely a H-UNCOVER felmérés adatait tartalmazza [8], ahol SARS-CoV-2 koronavírussal való, korábbi vagy aktív fertőzöttséget mutatták ki (tehát a már gyógyultak is számítanak, amíg a szervezetükben megtalálható a vírussal szembeni ellenanyag). Itt a konfidenciaintervallum 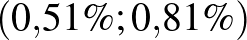 , vagyis az alsó és felső végpont között több mint másfélszeres szorzó van, ez meglehetősen nagy bizonytalanság például az
, vagyis az alsó és felső végpont között több mint másfélszeres szorzó van, ez meglehetősen nagy bizonytalanság például az 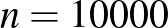 ,
, 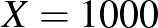 esethez hasonlítva, ahol a tesztek száma majdnem ugyanaz, de a betegségen átesettek aránya jóval nagyobb (ez persze csak elképzelt eset). Valójában pedig még hosszabb konfidenciaintervallumot kellene megadnunk, hiszen nem modelleztük a tesztek hibáját és más valós, torzításhoz vezető jelenségeket, és a közelítésünk hibáját is elhanyagoltuk (ezekről részletesebben az első rész [3] végén írtunk). A táblázathoz visszatérve, például
esethez hasonlítva, ahol a tesztek száma majdnem ugyanaz, de a betegségen átesettek aránya jóval nagyobb (ez persze csak elképzelt eset). Valójában pedig még hosszabb konfidenciaintervallumot kellene megadnunk, hiszen nem modelleztük a tesztek hibáját és más valós, torzításhoz vezető jelenségeket, és a közelítésünk hibáját is elhanyagoltuk (ezekről részletesebben az első rész [3] végén írtunk). A táblázathoz visszatérve, például 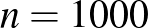 esetén
esetén 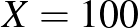 -ra az intervallum hosszának és az
-ra az intervallum hosszának és az 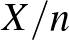 -nek az aránya 38%, míg
-nek az aránya 38%, míg 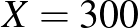 -ra csak 18,7%, vagyis a középső értékhez viszonyítva a második esetben rövidebbnek számít az intervallum. A képletből erre a hányadosra
-ra csak 18,7%, vagyis a középső értékhez viszonyítva a második esetben rövidebbnek számít az intervallum. A képletből erre a hányadosra 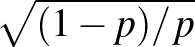 jellegű válasz adódik, ami annál nagyobb, minél kisebb a
jellegű válasz adódik, ami annál nagyobb, minél kisebb a  . Azaz relatív értelemben a fertőzöttek kis száma esetén csak jóval hosszabb konfidenciaintervallumot tudunk adni. Persze ilyenkor a fenti módszer sem feltétlenül használható, elromlik a közelítés (valójában a táblázatunk vonalak alatti soraiban sem volt teljesen jogos a feltételezés, hogy használhatjuk a közelítést), de ez a megállapítás érvényes marad. Hasonlóképpen az is látható a képletből, hogy rögzített (páros)
. Azaz relatív értelemben a fertőzöttek kis száma esetén csak jóval hosszabb konfidenciaintervallumot tudunk adni. Persze ilyenkor a fenti módszer sem feltétlenül használható, elromlik a közelítés (valójában a táblázatunk vonalak alatti soraiban sem volt teljesen jogos a feltételezés, hogy használhatjuk a közelítést), de ez a megállapítás érvényes marad. Hasonlóképpen az is látható a képletből, hogy rögzített (páros) 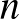 esetén a leghosszabb konfidenciaintervallumot akkor kapjuk, ha
esetén a leghosszabb konfidenciaintervallumot akkor kapjuk, ha 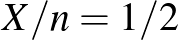 , azaz ugyanannyi fertőzött és egészséges embert találunk.
, azaz ugyanannyi fertőzött és egészséges embert találunk.
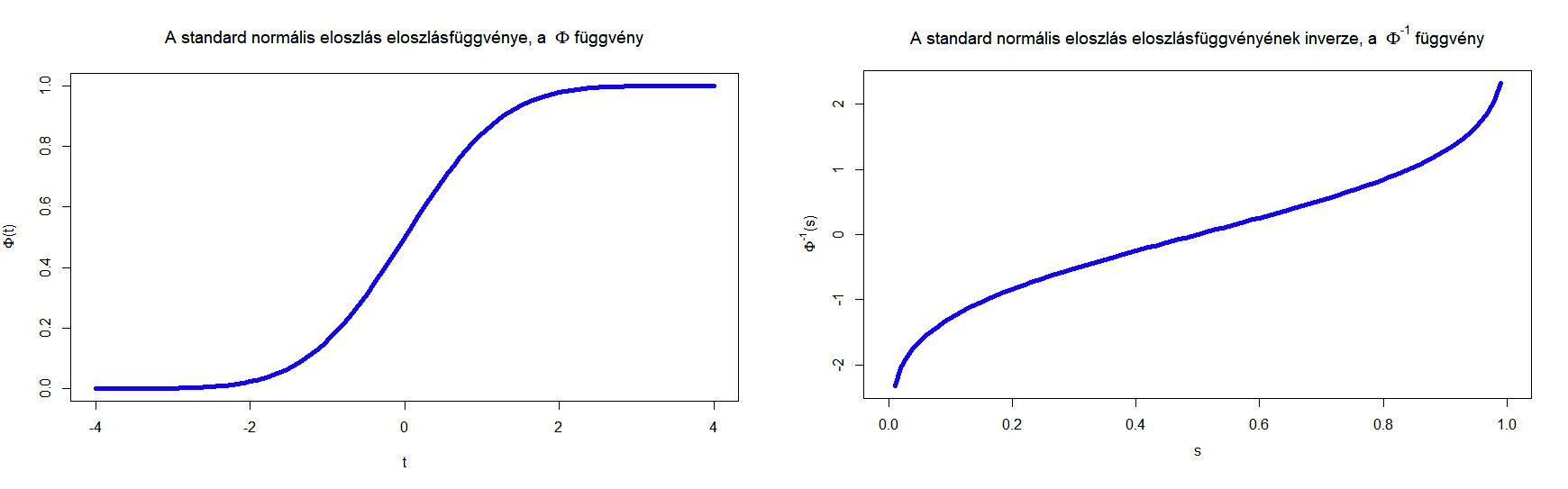
Megbízhatósági szint. Azt is kérdezhetjük, hogy hogyan függ a konfidenciaintervallum hossza a megbízhatósági szinttől, amit eddig 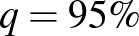 -nak választottunk. Általánosan felírva ugyanezt a számolást, ha
-nak választottunk. Általánosan felírva ugyanezt a számolást, ha 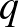 megbízhatósági szintű konfidenciaintervallumot szeretnénk:
megbízhatósági szintű konfidenciaintervallumot szeretnénk:
Az világos, hogy minél nagyobb 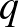 , vagyis minél nagyobb eséllyel kell tartalmaznia az intervallumnak a valódi értéket, annál nagyobb lesz a hossz. A képletből ez onnan látszik, hogy
, vagyis minél nagyobb eséllyel kell tartalmaznia az intervallumnak a valódi értéket, annál nagyobb lesz a hossz. A képletből ez onnan látszik, hogy  monoton növő függvény, ezért az inverze is az (2. ábra). Kérdés azonban, hogy mennyivel kell hosszabb intervallumot mondanunk, ha mondjuk 5% helyett csak 1% valószínűségű tévedést engedünk meg. Itt néhány szokásos választással, ahogy a 2. ábráról is leolvashatjuk:
monoton növő függvény, ezért az inverze is az (2. ábra). Kérdés azonban, hogy mennyivel kell hosszabb intervallumot mondanunk, ha mondjuk 5% helyett csak 1% valószínűségű tévedést engedünk meg. Itt néhány szokásos választással, ahogy a 2. ábráról is leolvashatjuk: 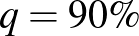 esetén
esetén 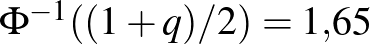 , ahogy már láttuk,
, ahogy már láttuk, 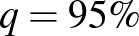 esetén 1,96 adódik,
esetén 1,96 adódik, 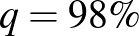 esetén 2,32, és
esetén 2,32, és 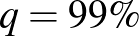 esetén 2,58. Ezeket megfigyelve megállapíthatjuk, hogy a konfidenciaintervallum hossza a szokásos értékek tartományában a megbízhatósági szinttől nem túl érzékenyen függ: az előbbi példában a tévedés valószínűségének ötödére csökkentése is csak nagyjából harmadával növeli az intervallum hosszát. Ugyanakkor egyrészt
esetén 2,58. Ezeket megfigyelve megállapíthatjuk, hogy a konfidenciaintervallum hossza a szokásos értékek tartományában a megbízhatósági szinttől nem túl érzékenyen függ: az előbbi példában a tévedés valószínűségének ötödére csökkentése is csak nagyjából harmadával növeli az intervallum hosszát. Ugyanakkor egyrészt  esetén a
esetén a 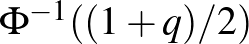 és így a konfidenciaintervallum hossza is végtelenhez tart, másrészt minél nagyobb megbízhatósági szintet írunk elő, annál nagyobb szerepe lehet a módszerből adódó hibáknak is, vagyis a konfidenciaintervallum hossza a képletből adódónál még nagyobb is lehet.
és így a konfidenciaintervallum hossza is végtelenhez tart, másrészt minél nagyobb megbízhatósági szintet írunk elő, annál nagyobb szerepe lehet a módszerből adódó hibáknak is, vagyis a konfidenciaintervallum hossza a képletből adódónál még nagyobb is lehet.
3. ábra. Konfidenciaintervallum két különböző mintaelemszám és megbízhatósági szint esetén
A 3. ábrán 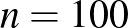 és
és 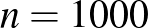 teszt esetén,
teszt esetén, 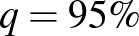 és
és 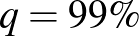 -os megbízhatósági szint mellett ábrázoltuk a konfidenciaintervallumot. A vízszintes tengelyen az
-os megbízhatósági szint mellett ábrázoltuk a konfidenciaintervallumot. A vízszintes tengelyen az 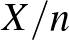 szerepel, ez tehát a betegek aránya a vizsgált emberek között, amit megfigyelünk. Ha ezt, illetve
szerepel, ez tehát a betegek aránya a vizsgált emberek között, amit megfigyelünk. Ha ezt, illetve 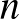 -t és
-t és 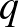 -t tudjuk, a két azonos színű pont adja meg a konfidenciaintervallum alsó, illetve felső határát. A konfidenciaintervallumok tehát a két-két azonos színű görbe között helyezkednek el. Itt is láthatjuk, hogy a 95% helyett 99%-os megbízhatósági szint nem jelent nagyságrendi különbséget a konfidenciaintervallum hosszában, azonban tízszer annyi tesztet elvégezve is csak nagyjából elharmadolni tudjuk a konfidenciaintervallumot. Azt is láthatjuk, hogy adott
-t tudjuk, a két azonos színű pont adja meg a konfidenciaintervallum alsó, illetve felső határát. A konfidenciaintervallumok tehát a két-két azonos színű görbe között helyezkednek el. Itt is láthatjuk, hogy a 95% helyett 99%-os megbízhatósági szint nem jelent nagyságrendi különbséget a konfidenciaintervallum hosszában, azonban tízszer annyi tesztet elvégezve is csak nagyjából elharmadolni tudjuk a konfidenciaintervallumot. Azt is láthatjuk, hogy adott 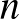 esetén a leghosszabb konfidenciaintervallum
esetén a leghosszabb konfidenciaintervallum 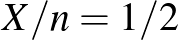 környékén adódik, a ritka, illetve nagyon gyakori betegség esetében pedig egyre rövidebb intervallumokat kapunk.
környékén adódik, a ritka, illetve nagyon gyakori betegség esetében pedig egyre rövidebb intervallumokat kapunk.
3. Becslés a valószínűségek alapján
A konfidenciaintervallum esetében is természetesnek vettük, hogy az 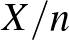 , vagyis a betegek relatív gyakorisága kerül középre – cikkünk második felében egy olyan gyakran használt statisztikai becslési módszert mutatunk be, ami ennek alátámasztására is alkalmazható.
, vagyis a betegek relatív gyakorisága kerül középre – cikkünk második felében egy olyan gyakran használt statisztikai becslési módszert mutatunk be, ami ennek alátámasztására is alkalmazható.
Példaképpen tegyük fel, hogy 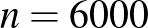 ember közül
ember közül 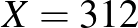 beteget találtunk, vagyis nagyjából minden huszadik ember volt beteg. A kérdés az, hogy mennyi lehet a betegek valódi aránya, vagyis mennyi annak
beteget találtunk, vagyis nagyjából minden huszadik ember volt beteg. A kérdés az, hogy mennyi lehet a betegek valódi aránya, vagyis mennyi annak  valószínűsége, hogy egy véletlenszerűen választott ember beteg. A lehetőségek száma végtelen, úgyhogy először megpróbálhatunk megelégedni azzal, hogy két lehetőségből megpróbáljuk eltalálni, hogy melyik lehetett a jó. Például tegyük fel, hogy a laboratóriumba ez a minta egy másikkal együtt érkezett, és azt is tudjuk, hogy ezek közül az egyik egy ritkábban lakott vidéki terület településeiből származik, ahol a fertőzöttek aránya egyéb vizsgálatok alapján
valószínűsége, hogy egy véletlenszerűen választott ember beteg. A lehetőségek száma végtelen, úgyhogy először megpróbálhatunk megelégedni azzal, hogy két lehetőségből megpróbáljuk eltalálni, hogy melyik lehetett a jó. Például tegyük fel, hogy a laboratóriumba ez a minta egy másikkal együtt érkezett, és azt is tudjuk, hogy ezek közül az egyik egy ritkábban lakott vidéki terület településeiből származik, ahol a fertőzöttek aránya egyéb vizsgálatok alapján 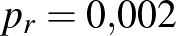 , míg a másikat egy sűrűn lakott nagyváros lakosaitól gyűjtötték, ahol a fertőzöttek valódi aránya
, míg a másikat egy sűrűn lakott nagyváros lakosaitól gyűjtötték, ahol a fertőzöttek valódi aránya 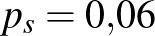 . Azonban elmulasztották a dobozokon feltüntetni, hogy melyik minta melyik, így el kellene dönteni, hogy a fenti
. Azonban elmulasztották a dobozokon feltüntetni, hogy melyik minta melyik, így el kellene dönteni, hogy a fenti 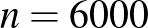 nagyságú minta a ritkán vagy a sűrűn lakott területről származik-e. Kizárni egyik lehetőséget sem tudjuk, hiszen mindkét esetben előfordulhat, hogy pontosan 312 beteget találunk. A betegek várható száma a ritkán lakott vidéken
nagyságú minta a ritkán vagy a sűrűn lakott területről származik-e. Kizárni egyik lehetőséget sem tudjuk, hiszen mindkét esetben előfordulhat, hogy pontosan 312 beteget találunk. A betegek várható száma a ritkán lakott vidéken 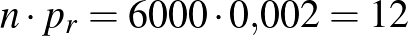 , és ebből azt is sejthetjük, hogy óriási balszerencse kellene ahhoz, hogy ennek majdnem harmincszorosa legyen a talált betegek száma. A sűrűn lakott városban
, és ebből azt is sejthetjük, hogy óriási balszerencse kellene ahhoz, hogy ennek majdnem harmincszorosa legyen a talált betegek száma. A sűrűn lakott városban 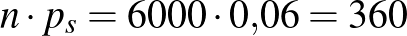 a betegek számának várható értéke, ez alapján a 312 egyáltalán nem tűnik elképzelhetetlennek. Vagyis, bár a 312 beteg mindkét esetben előfordulhat, a sűrűn lakott városban ez jóval valószínűbb lehetőség, mint a ritkán lakott vidéken. Ezeket a valószínűségeket szerencsére ki is tudjuk számolni, az alapján, hogy az
a betegek számának várható értéke, ez alapján a 312 egyáltalán nem tűnik elképzelhetetlennek. Vagyis, bár a 312 beteg mindkét esetben előfordulhat, a sűrűn lakott városban ez jóval valószínűbb lehetőség, mint a ritkán lakott vidéken. Ezeket a valószínűségeket szerencsére ki is tudjuk számolni, az alapján, hogy az 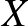 valószínűségi változó binomiális eloszlású [2,5,10].
valószínűségi változó binomiális eloszlású [2,5,10].
Annak valószínűsége, hogy a ritkán lakott vidéken pontosan 312 beteget találunk 6000 ember között:
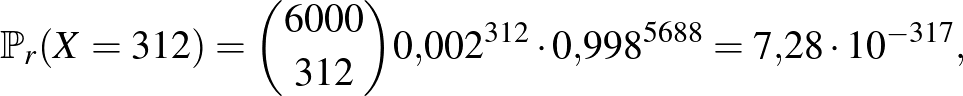
vagyis valóban, lehetséges, hogy a ritkán lakott vidéken ennyi beteget találunk, de ennek valószínűsége kisebb, mint hogy 40 egymást követő héten telitalálatunk lesz a lottón (egy-egy héten 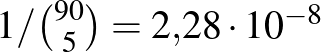 valószínűséggel lesz ötből öt találatunk).
valószínűséggel lesz ötből öt találatunk).
Annak valószínűsége, hogy a sűrűn lakott városban pontosan 312 beteget találunk 6000 ember között:
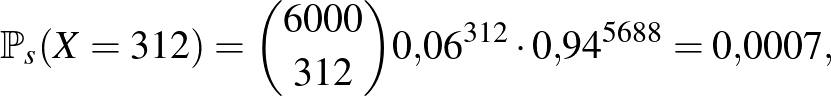
ami szintén nem túlságosan nagy, de az előző lehetőségnél sok nagyságrenddel nagyobb (például több, mint a lottón a négy találat valószínűsége). Vagyis, az alapján, hogy az általunk megfigyelt történés mennyire valószínű a 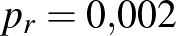 , illetve
, illetve 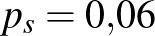 esetekben, arra következtethetünk, hogy ez az a minta a kettő közül, ami a sűrűn lakott nagyvárosból származik. A tévedésünk nincs kizárva, de a valószínűségek közötti nagyságrendi különbség nyomós érv az állításunk mellett.
esetekben, arra következtethetünk, hogy ez az a minta a kettő közül, ami a sűrűn lakott nagyvárosból származik. A tévedésünk nincs kizárva, de a valószínűségek közötti nagyságrendi különbség nyomós érv az állításunk mellett.
Ez tehát akkor működött, amikor feltételeztük, hogy a betegség valószínűsége két lehetséges érték valamelyike. Ha nincs semmilyen előzetes információnk, akkor a  értéke bármilyen 0 és 1 közötti szám lehet (a határokat nem beleértve), kizárni egyik lehetőséget sem tudjuk. Azonban a fent látott módszer akkor is működik, ha több lehetőségünk van. Annyit kell csak tennünk, hogy felírjuk, hogy ha adott
értéke bármilyen 0 és 1 közötti szám lehet (a határokat nem beleértve), kizárni egyik lehetőséget sem tudjuk. Azonban a fent látott módszer akkor is működik, ha több lehetőségünk van. Annyit kell csak tennünk, hogy felírjuk, hogy ha adott  mellett mennyi annak valószínűsége, hogy a 6000 vizsgálatból pontosan 312 jelez betegséget, majd megkeressük azt a
mellett mennyi annak valószínűsége, hogy a 6000 vizsgálatból pontosan 312 jelez betegséget, majd megkeressük azt a  -t, amire ez a legnagyobb – hiszen éppen ezt tettük az előbb is, a két lehetőségből a nagyobb valószínűséget adó
-t, amire ez a legnagyobb – hiszen éppen ezt tettük az előbb is, a két lehetőségből a nagyobb valószínűséget adó  -t választva. A kérdés tehát az, hogy milyen
-t választva. A kérdés tehát az, hogy milyen 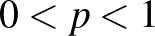 esetén lesz a legnagyobb az alábbi valószínűség:
esetén lesz a legnagyobb az alábbi valószínűség:
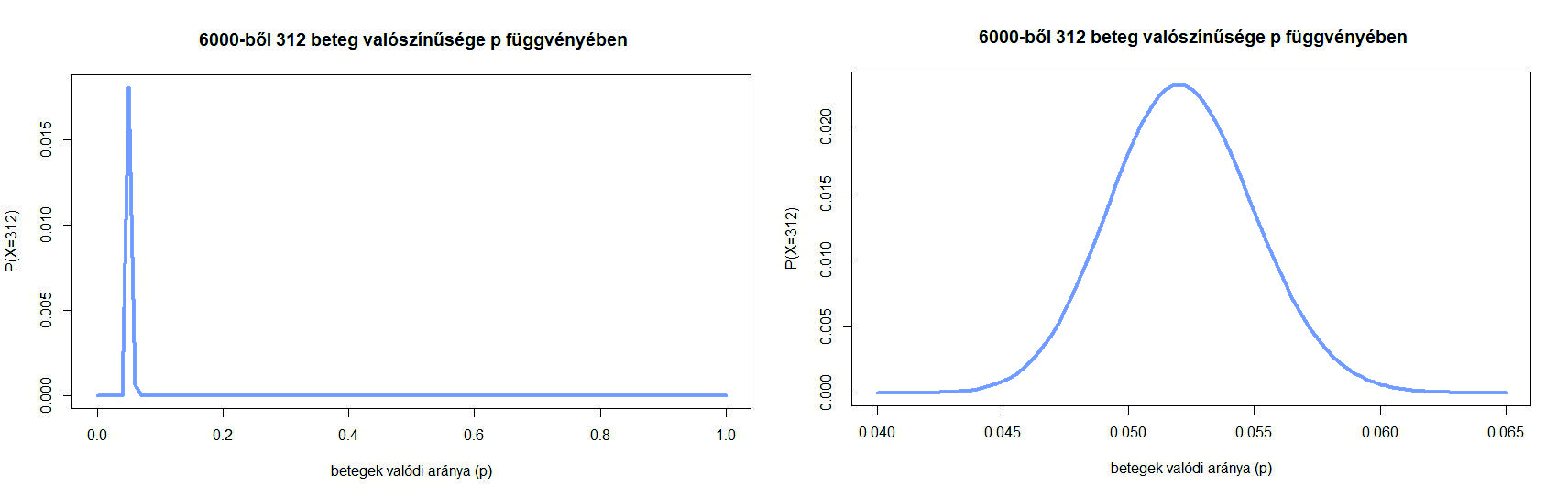
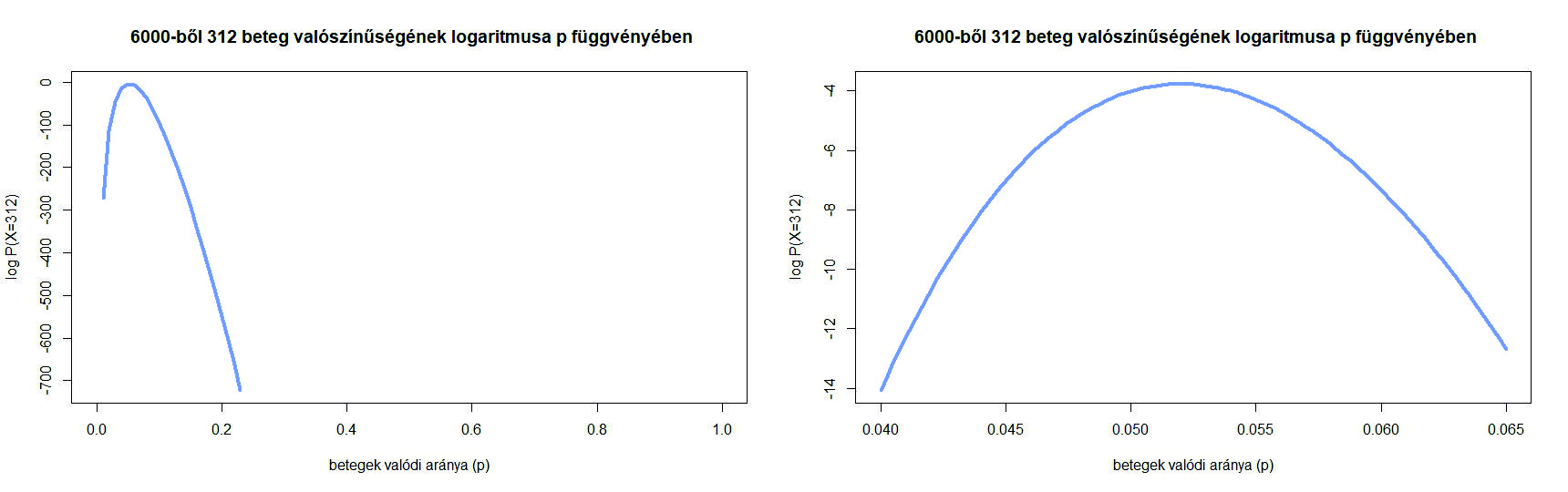
4. ábra. A 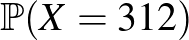 valószínűség a betegek valódi arányának,
valószínűség a betegek valódi arányának,  -nek függvényében
-nek függvényében
Ezt a függvényt a 4. ábrán láthatjuk (bal oldalon a teljes 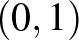 intervallumon, a jobb oldalon belenagyítva a maximum környékére). Azt látjuk, hogy a korábbi
intervallumon, a jobb oldalon belenagyítva a maximum környékére). Azt látjuk, hogy a korábbi 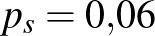 nem a lehető legnagyobb valószínűséget adja, ennél kicsit kisebb
nem a lehető legnagyobb valószínűséget adja, ennél kicsit kisebb  -vel még nagyobb lesz a valószínűsége a 312 betegnek. A maximumhely (az a szám, ahol a függvény a legnagyobb értéket veszi fel) meghatározására az analízisből ismert deriválás módszerét használjuk – de csak egy előkészítő lépés után. Ugyanis az előző egyenlet jobb oldalán egy szorzat szerepel, és szorzatot deriválni ugyan nem lehetetlen, de bonyolultabb, mint összeget deriválni, ahol tagonként végezhető el ez a művelet. Ezért kéne egy függvény, ami szorzatból összeget csinál, és ami ráadásul lehetőleg monoton növő, hogy a maximumhelyet ne mozgassa el. Éppen ilyen függvény a logaritmus. Ezért azt a kérdést, hogy milyen
-vel még nagyobb lesz a valószínűsége a 312 betegnek. A maximumhely (az a szám, ahol a függvény a legnagyobb értéket veszi fel) meghatározására az analízisből ismert deriválás módszerét használjuk – de csak egy előkészítő lépés után. Ugyanis az előző egyenlet jobb oldalán egy szorzat szerepel, és szorzatot deriválni ugyan nem lehetetlen, de bonyolultabb, mint összeget deriválni, ahol tagonként végezhető el ez a művelet. Ezért kéne egy függvény, ami szorzatból összeget csinál, és ami ráadásul lehetőleg monoton növő, hogy a maximumhelyet ne mozgassa el. Éppen ilyen függvény a logaritmus. Ezért azt a kérdést, hogy milyen  -re lesz a
-re lesz a 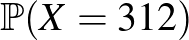 valószínűség a lehető legnagyobb, a következőképpen fogalmazzuk át. Milyen
valószínűség a lehető legnagyobb, a következőképpen fogalmazzuk át. Milyen 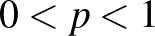 számra lesz az alábbi kifejezés maximális:
számra lesz az alábbi kifejezés maximális:
5. ábra. A 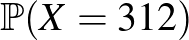 valószínűség logaritmusa a betegek valódi arányának,
valószínűség logaritmusa a betegek valódi arányának,  -nek függvényében
-nek függvényében
Itt tehát a (4) egyenlet jobb oldalának logaritmusát vettük. Ez a függvény az 5. ábrán látható, amit az előzővel összehasonlítva le is olvashatjuk, hogy bár a két függvény eltérő alakú és más értékeket vesz fel, a maximumhelyük ugyanaz – ami a logaritmus monoton növő tulajdonságából következik is. Tehát nincs más hátra, mint hogy deriválással megkeressük azt a  számot, amelyre az (5) értéke maximális. A jobb oldalt deriválva (az első tag nem függ
számot, amelyre az (5) értéke maximális. A jobb oldalt deriválva (az első tag nem függ  -től, ennek deriváltja 0, ezen kívül a
-től, ennek deriváltja 0, ezen kívül a 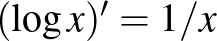 összefüggést és az összetett függvény deriválására vonatkozó szabályt használjuk):
összefüggést és az összetett függvény deriválására vonatkozó szabályt használjuk):
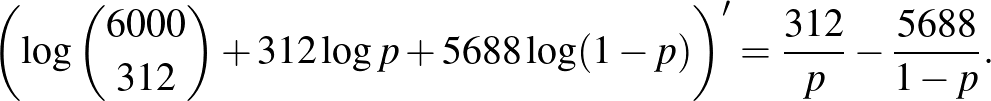
A maximumhelyet ott kell keresnünk, ahol a derivált, vagyis az érintő meredeksége nulla, ahogy ezt az 5. ábra is sugallja. Az egyenletet megoldva:
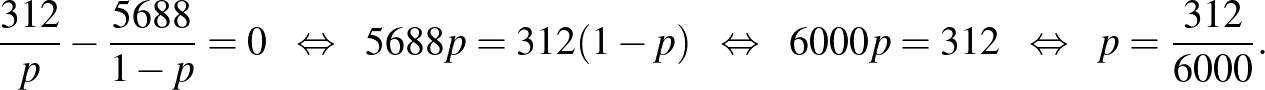
Sajnos, ahogy analízisórán minden bizonnyal felhívták rá a figyelmünket, az, hogy a derivált 0, nem elég ahhoz, hogy szélsőértékhelyet találjunk. Azonban ebben az esetben azt mondhatjuk, hogy a második derivált, 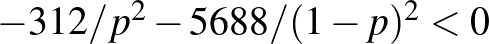 , és ebből következik, hogy itt lokális maximumhely van, az intervallum szélein pedig
, és ebből következik, hogy itt lokális maximumhely van, az intervallum szélein pedig 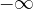 a határérték, ott nem lehet maximumhely, vagyis ez globális maximumhely is. Egy másik érvelés ugyanerre: az egyenlet helyett egyenlőtlenségeket írva az is látható, hogy a derivált pontosan akkor pozitív, ha
a határérték, ott nem lehet maximumhely, vagyis ez globális maximumhely is. Egy másik érvelés ugyanerre: az egyenlet helyett egyenlőtlenségeket írva az is látható, hogy a derivált pontosan akkor pozitív, ha 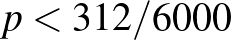 . Vagyis
. Vagyis 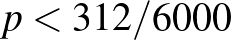 esetén a függvény szigorúan monoton növő,
esetén a függvény szigorúan monoton növő, 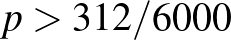 esetén pedig szigorúan monoton csökkenő, ebből már következik, hogy ebben a pontban veszi fel a legnagyobb értéket.
esetén pedig szigorúan monoton csökkenő, ebből már következik, hogy ebben a pontban veszi fel a legnagyobb értéket.
A gondolatmenetet a következőképpen fejezhetjük be: deriválás segítségével megállapítottuk, hogy 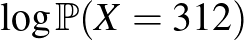 a
a 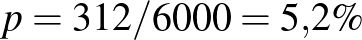 érték esetén a legnagyobb. Mivel a logaritmusfüggvény szigorúan monoton növő, azaz minél nagyobb
érték esetén a legnagyobb. Mivel a logaritmusfüggvény szigorúan monoton növő, azaz minél nagyobb 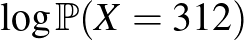 , annál nagyobb
, annál nagyobb 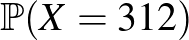 is, ebből következik, hogy
is, ebből következik, hogy 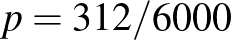 lesz az érték, amelyre
lesz az érték, amelyre 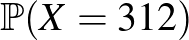 a legnagyobb (ez összhangban van az ábrával is). És, bár természetesen
a legnagyobb (ez összhangban van az ábrával is). És, bár természetesen  becslésekor más szempontokat is lehetne választani, most azt tűztük ki célnak, hogy azt a
becslésekor más szempontokat is lehetne választani, most azt tűztük ki célnak, hogy azt a  -t választjuk, amelyre a legnagyobb a valószínűsége annak az esetnek, amit megfigyeltünk. Tehát
-t választjuk, amelyre a legnagyobb a valószínűsége annak az esetnek, amit megfigyeltünk. Tehát  becslése
becslése 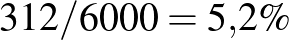 lesz a fent vázolt módszer alapján, amelyet maximumlikelihood-módszernek neveznek. A fenti érvelésben a számokat tetszőlegesen választhatjuk, vagyis azt láttuk be, hogy ha
lesz a fent vázolt módszer alapján, amelyet maximumlikelihood-módszernek neveznek. A fenti érvelésben a számokat tetszőlegesen választhatjuk, vagyis azt láttuk be, hogy ha 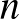 vizsgált ember közül
vizsgált ember közül 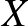 beteget találtunk, akkor a betegség valódi gyakoriságának
beteget találtunk, akkor a betegség valódi gyakoriságának  értékére a maximumlikelihood-módszerrel adott becslés
értékére a maximumlikelihood-módszerrel adott becslés
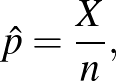
azaz a betegek aránya a vizsgált mintában. Ezzel a (3) képlet olyan értelemben megerősítést nyert, hogy ez alapján a módszer alapján jogos az ismeretlen  helyébe
helyébe 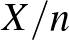 -t helyettesíteni a konfidenciaintervallum építésekor. Illetve, mivel a H-UNCOVER vizsgálatban
-t helyettesíteni a konfidenciaintervallum építésekor. Illetve, mivel a H-UNCOVER vizsgálatban 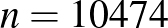 vizsgált ember közül
vizsgált ember közül 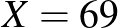 teszt lett pozitív, a 2020 májusáig COVID-19 fertőzésen átesett magyar állampolgárok arányát az
teszt lett pozitív, a 2020 májusáig COVID-19 fertőzésen átesett magyar állampolgárok arányát az 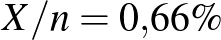 értékkel becsülhetjük az előzőek alapján [8].
értékkel becsülhetjük az előzőek alapján [8].
A maximumlikelihood-módszer más esetekben is használható [4,7]. Általában van egy ismeretlen mennyiség (paraméter), ez volt esetünkben  , a betegek valódi aránya. Elvégzünk valamilyen kísérletet, ez alapján becsüljük az ismeretlen értéket. Ha ezt úgy tesszük, hogy azt az értéket választjuk, amely esetén annak valószínűsége, hogy az általunk a kísérlet során megfigyelt esemény következik be, a lehető legnagyobb legyen, akkor a maximumlikelihood-módszert alkalmaztuk. Nem minden esetben, de az is gyakori, hogy ilyenkor a valószínűség logaritmusának maximumhelyét keressük meg deriválás segítségével. Azonban, ahogy a legtöbb statisztikai módszer, a maximumlikelihood-becslés sem minden esetben működik, például nincs mindig egyértelmű maximumhely, és egyéb hátrányai is lehetnek, például a várható értéke eltérhet a becsülni kívánt értéktől (vagyis torzíthat), vagy a példában
, a betegek valódi aránya. Elvégzünk valamilyen kísérletet, ez alapján becsüljük az ismeretlen értéket. Ha ezt úgy tesszük, hogy azt az értéket választjuk, amely esetén annak valószínűsége, hogy az általunk a kísérlet során megfigyelt esemény következik be, a lehető legnagyobb legyen, akkor a maximumlikelihood-módszert alkalmaztuk. Nem minden esetben, de az is gyakori, hogy ilyenkor a valószínűség logaritmusának maximumhelyét keressük meg deriválás segítségével. Azonban, ahogy a legtöbb statisztikai módszer, a maximumlikelihood-becslés sem minden esetben működik, például nincs mindig egyértelmű maximumhely, és egyéb hátrányai is lehetnek, például a várható értéke eltérhet a becsülni kívánt értéktől (vagyis torzíthat), vagy a példában 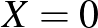 -ra kevésbé jól működik. Ugyanakkor megfelelő feltételek mellett (és ezek a fenti példában is teljesülnek) a mintaelemszámmal végtelenhez tartva már jó tulajdonságokkal rendelkezik, a várható értéke tart a valódi paraméterhez, és a szórása is a lehető legkisebb értékhez, vagyis a bizonytalanságot minimalizálja. Ezzel együtt, bár ezekre nem térünk ki, statisztikai feladatokban érdemes több módszert is megvizsgálni (például momentummódszer, Bayes-becslés [4,7]) és azt választani, amelyikkel az adott problémát a legjobban meg tudjuk oldani.
-ra kevésbé jól működik. Ugyanakkor megfelelő feltételek mellett (és ezek a fenti példában is teljesülnek) a mintaelemszámmal végtelenhez tartva már jó tulajdonságokkal rendelkezik, a várható értéke tart a valódi paraméterhez, és a szórása is a lehető legkisebb értékhez, vagyis a bizonytalanságot minimalizálja. Ezzel együtt, bár ezekre nem térünk ki, statisztikai feladatokban érdemes több módszert is megvizsgálni (például momentummódszer, Bayes-becslés [4,7]) és azt választani, amelyikkel az adott problémát a legjobban meg tudjuk oldani.
4. Összefoglalás
Kétrészes cikkünkben azt vizsgáltuk, hogy milyen valószínűségszámítási és statisztikai módszerek alkalmazhatók, ha egy betegség gyakoriságát véletlenszerű teszteléssel akarjuk megbecsülni. Láttuk, hogy az, hogy a betegek valódi arányához képest hány százalékot tévedhetünk felfelé vagy lefelé, nagyobb hatással lehet az elvégzett tesztek számára, mint az, ha a helyes döntés valószínűségére adunk meg egy szigorúbb korlátot: kétszer nagyobb pontossághoz vagy feleolyan hosszú konfidenciaintervallumhoz négyszer annyi teszt kellett, viszont 95% helyett 99%-os megbízhatóságot előírva nem nőtt ennyire a szükséges vizsgálatok száma. Azt is láttuk, hogy ha az abszolút hiba helyett a relatív hibát akarjuk alacsonyan tartani, akkor ritka, 1% vagy 0,1% körüli gyakoriság esetén is jelentősen nagyobb mintaelemszámmal kell számolnunk. Az alkalmazott módszer a binomiális eloszlásnak a normális eloszlással való közelítése volt a de Moivre–Laplace-tétel, vagyis a centrális határeloszlástétel egy speciális esete alapján, itt szintén arra kellett figyelni, hogy ha a betegség túlságosan ritka, akkor vagy más módszert kell keresnünk, vagy ismét csak nagy mintaelemszámot választani – ez azonban valamennyire természetes is, 0,1% nagyságrendű valószínűség esetén 10 vagy 100 teszt semmilyen módszerrel nem lenne megfelelő egy pontos becsléshez. Emellett arra is kitértünk, hogy a valós alkalmazásokban milyen nehezítő körülmények lépnek fel (a tesztek hibája, az egyenletes mintavételezés nehézségei), amelynek következtében a számolások egy ideális eset vizsgálatának, a kapott eredmények pedig a szükséges tesztek számának alsó becslésének tekinthetők.
Irodalomjegyzék
- [1] Douglas Altman, David Machin, Trevor Bryant, Martin Gardner, Statistics with Confidence: Confidence Intervals and Statistical Guidelines. Second Edition, John Wiley & Sons, New York, 2000.
[2] Arató Miklós, Prokaj Vilmos, Zempléni András, Bevezetés a valószínűségszámításba és alkalmazásaiba: példákkal, szimulációkkal, 2013. https://ttk.elte.hu/dstore/document/901/zempleni.pdf
[3] Backhausz Ágnes, Simon L. Péter, Mennyit teszteljünk? 1. rész, Érintő, 2020. június. https://ematlap.hu/index.php?option=com_content&view=article&id=956:mennyit-teszteljunk-take-1&catid=234&Itemid=827
[4] Bolla Marianna, Krámli András, Statisztikai következtetések elmélete. Második kiadás, Typotex, 2012.
[5] Csiszár Villő, Valószínűségszámítás 1. http://csvillo.web.elte.hu/mtval/jegyzet.pdf
[6] William Feller, An introduction to probability theory and its applications. Vol. I. Third edition, John Wiley & Sons, Inc., New York, 1968.
[7] David Freedman, Robert Pisani, Roger Purves, Statistics. Fourth edition, W. W. Norton & Company, New York, 2007.
[8] Béla Merkely, Attila J. Szabó, Annamária Kosztin et al., Novel coronavirus epidemic in the Hungarian population, a cross-sectional nationwide survey to support the exit policy in Hungary. GeroScience 42, 1063–1074 (2020). https://link.springer.com/article/10.1007/s11357-020-00226-9
[9] R. G. Newcombe, Confidence intervals for proportions and related measures of effect size. Chapman & Hall/CRC Biostatistics Series, CRC Press, Boca Raton, FL, 2013.
[10] Sheldon Ross, A first course in probability. Second edition, Macmillan Co., New York, 1984.