Mi is ... a csáp?

A csáp (angolul grope, ami „tapogatózást” jelent) egy matematikai kifejezés, amely nyomtatásban először Jim Cannon 1978-as Bulletinben közölt cikkében [1] jelent meg. Ő a kifejezés kitalálójának egy madisoni geometriai topológus kollégáját, Russ McMillant tartotta. Cannon elmagyarázta, hogy azért nevezték ezt a dolgot csápnak, mert „számos tapogatózó ujj nő ki belőle”. Arra is felhívta a figyelmet, hogy „ez a szóhasználat rossz szóviccekhez vezethet” – némelyiknek ő sem tudott ellenállni. Az évek során még publikálásra szánt cikkek is vissza lettek utasítva, mert használták a csáp szót.

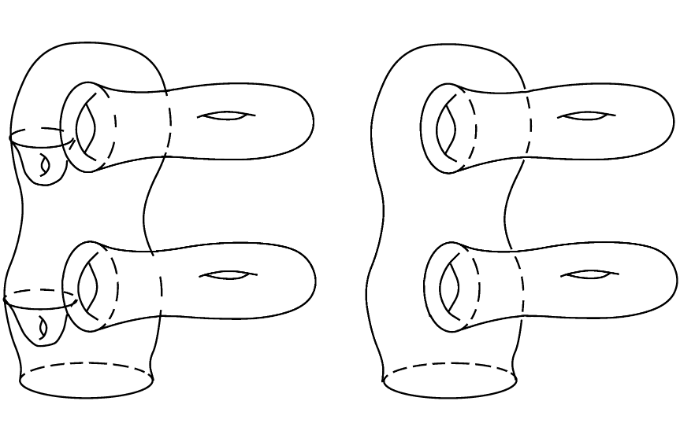
2 magasságú (balra) és 3 osztályú (jobbra) csápok

Matematikailag egy csáp egy bizonyos $2$ -dimenziós komplexus (amelynek egy körvonal a határa), amely felületek uniója (ahol felületen egy kompakt, összefüggő, irányított $2$ -dimenziós sokaságot értünk egy határoló körvonallal). Ahhoz, hogy beszélhessünk arról, hogyan vannak ezek a felületek összeragasztva, egy komplexitást mérő fogalmat, a csáp magasságát vezetjük be. Ha a csáp $h$ magassága $1$ , akkor a csáp csak egy $\Sigma$ felület. Ha $i = 1, \ldots, 2g(\Sigma)$ , ahol $g(\Sigma)$ a $\Sigma$ felület génusza, akkor alkossák az $\alpha_i$ -k a $\Sigma$ felület egy körökből álló teljes szimplektikus bázisát. Ekkor egy $h+1$ magasságú csápot úgy kapunk, hogy $h$ magasságú csápokat ragasztunk az $\alpha_i$ -khez a csápok határoló körei mentén.

Ezért a csápok nem sokaságok, de az előforduló szingularitásaik nagyon egyszerű típusúak, úgyhogy ezek a $2$ -komplexusok bizonyos értelemben a felületek után a legegyszerűbb terek. Hogy motiváljuk a csápok és magasságuk definíciójának bevezetését, a következőkben elmagyarázzuk, hogyan kapcsolódik mindez a csoportelmélethez.

Csoport kommutátorok és csápok

Egy $S^1 \to X$ (a körvonalból valamilyen $X$ térbe menő) folytonos leképezés a $\pi_1(X)$ fundamentális csoportnak egy elemét reprezentálja. Ez a leképezés pontosan akkor terjed ki valamilyen felületnek (azaz egy 1 magasságú csápnak) az $X$ -be menő leképezésévé, ha egy kommutátort reprezentál $\pi_1(X)$ -ben. Ezt úgy láthatjuk a legkönnyebben, hogy a $g$ génuszú $\Sigma$ felületre mint párosított oldalakkal rendelkező (és középen kilyukasztott) $4g$ -szögre gondolunk. Ezt a párosítást úgy kapjuk, hogy vesszük a következő szót a $4g$ -szög határának mentén:

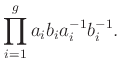
$\displaystyle \prod_{i = 1}^g a_i b_i a_i^{-1} b_i^{-1}.$

Mivel $\Sigma$ határoló köre a $4g$ -szög közepén helyezkedik el, ezzel a kommutátorral kell megegyeznie. Iterált kommutátorok hasonlóan fejezhetők ki csápok $X$ -be menő folytonos leképezéseivel: egy $S^1 \to X$ leképezés pontosan akkor reprezentálja $\pi_1(X)$ leszálló lánca $h$ -adik tagjának egy elemét, ha kiterjed egy $h$ magasságú csáp folytonos leképezésévé. Emlékeztetünk rá, hogy egy $G=G^{(0)}$ csoport leszálló lánca a $G^{(h+1)} := [G^{(h)}, G^{(h)}]$ iterált kommutátorokkal van definiálva. A csoport feloldható, ha ez a sorozat $1$ -ben végződik. A leszálló láncnak egy közeli rokona az alsó centrális lánc, melyet a $G = G_1$ csoportra a $G_{c+1} = [G, G_c]$ definícióval adunk meg. A csoport nilpotens, ha ez a sorozat $1$ -ben végződik. Az olvasó megpróbálhatja elképzelni hogyan definiáljunk bizonyos $2$ -komplexusokat (egy határoló körvonallal), amelyeket $c$ osztályú csápoknak hívunk, úgy, hogy egy $S^1 \to X$ leképezés pontosan akkor reprezentáljon egy elemet $\pi_1(X)$ alsó centrális láncának $c$ -edik tagjában, ha kiterjed egy $c$ osztályú csáp folytonos leképezésévé. Valójában az ilyen csápok általánosabbak, mint amelyeket legelőször definiáltunk, és a szóhasználat meg is változott az évek során: a $h$ magasságú csápokat ma szimmetrikus csápoknak is nevezzük. Ezek a csoportelmélet szerint $c = 2^h$ osztályúak. Nem minden csáp szimmetrikus, ahogy azt a fenti ábra is mutatja.

Geometriai csoport kommutátorok

Ahogyan csápok leképezéseivel leírhatunk iterált kommutátorokat $\pi_1(X)$ -ben, nézhetünk beágyazott csápokat is ahhoz, hogy több geometriai kérdést tanulmányozzunk. Ezeknek a legközvetlenebb felhasználása tűnik a legaktuálisabbnak, és ezt a csomóelmélet témakörében találjuk. A csomóelmélet a $3$ -dimenziós térbe beágyazott körök elmélete (ami más, mint a körök folytonos leképezéseié a fundamentális csoport esetében). Emlékeztetünk rá, hogy minden csomó határol egy Seifert felületet a $3$ -dimenziós térben, de csak a triviális csomó határol beágyazott körlapot. Ezért az egész csomóelmélet a felületek és a körlap közötti különbségből ered. Ahogy láttuk, ez pont olyan, mint a különbség egy $\pi_1(X)$ -beli kommutátor és a csoportbeli egységelem között. A csápok lehetőséget adnak arra, hogy filtráljuk ezt a különbséget, hasonlóan a csoportelméletbeli iterált kommutátorokhoz.

$4$ -dimenzióban gondolkodva oda jutunk, hogy $S^3 = \partial D^4$ -ben tanulmányozzuk a csomókat, amik kiterjednek $h$ magasságú szimmetrikus csápok $D^4$ -be való beágyazásaivá. Ez a csomó konkordizmuscsoport egy filtrálását adja meg, melyet Cochran, Orr és Teichner vezettek be 1998-ban. Megmutatták, hogy az összes előzőleg ismert konkordizmus invariáns megkapható ebből kis $h$ -ra. Például ha a csomó egy $4$ magasságú szimmetrikus csápot határol $D^4$ -ben, akkor az összes Casson-Gordon-invariánsa eltűnik. A csomó komplementumának feloldható fedéseivel és annak von Neumann-szignatúráival megmutatták továbbá, hogy ennek a filtrációnak minden egymás után következő faktora nemtriviális.

Schneiderman bebizonyította, hogy minden csomó, amelynek triviális az Arf-invariánsa, határol valamilyen tetszőlegesen nagy osztályú (nemszimmetrikus) csápot $D^4$ -ben. Viszont ha ilyen csápot a $3$ -dimenziós térbe ágyazva keresünk, akkor egy gazdag obstrukcióelméletet kapunk. Ezt Conant és Teichner dolgozta ki, és szorosan kapcsolódik a Vassiliev-féle csomóinvariánsokhoz, ahol a csáp osztálya pontosan megfelel az invariáns véges típusának.

A csápok ezen $3$ - és $3.5$ -dimenziós alkalmazásainak áttekintéséhez és további hivatkozásokhoz [3]-at ajánljuk.

A csápok rövid története

Csápokhoz hasonló objektumok először 1971-ben tűntek fel Stanko egy cikkében, aki megmutatta, hogy bizonyos $3$ kodimenziós vad beágyazások sima beágyazásokat közelítenek meg. 1975-ben Cannon és Ancel kiterjesztették Stanko technikáját $1$ kodimenzióra. 1977-ben Cannon bevezette a csápokat és a diszjunkt körlap tulajdonságot, hogy bebizonyítson számos sokaság-felismerési tételt. Közöttük volt a híres Kétszeres szuszpenzió tétel, ami azt állítja, hogy egy tetszőleges $n$ -dimenziós homologikus gömb kétszeres szuszpenziója homeomorf a standard $(n+2)$ -dimenziós gömbbel. (Egy $X$ tér szuszpenziója az $X$ két kúpjának $X$ mentén vett uniója.) Az eredmény rendkívül meglepő volt, mivel egy $X$ sokaság egyszeri szuszpenziója csak akkor lehet sokaság, ha $X$ a standard gömb. Cannon előtt, és csápok használata nélkül Bob Edwards sok egyedi esetben bebizonyította a kétszeres szuszpenzió tételt (és belátta a Háromszoros szuszpenzió tételt). De ezen problémák megoldásában a csápok olyan sikeresnek bizonyultak, hogy Edwards azt javasolta, $4$ -dimenziós topológiában is használják őket. Michael Freedman vezette be őket az 1983-as varsói Nemzetközi Matematikai Kongresszus kiadványában megjelent cikkében. Ebben a cikkben kiterjesztette a Körlap beágyazási tételét az egyszeresen összefüggő esetről jó fundamentális csoporttal rendelkező $4$ -sokaságokra. Ez magában foglalta a véges és ciklikus csoportokat (de még mindig nyitott kérdés, hogy mely csoportok jók, pillanatnyilag a szubexponenciális növekedésű csoportok a legáltalánosabb ismert osztály). A [2] monográfiában a $4$ -sokaságok topologikus elmélete teljes egészében a szimmetrikus csápokkal lett megfogalmazva.

Érdekes megfigyelni, hogyan tolódott a csápok felhasználása az évek során egyre alacsonyabb dimenziókba. A szlogen azonban mindig ugyanaz maradt: ha egy körlapot keresel, próbálj meg először egy csápot találni.

Peter Teichner

Irodalomjegyzék

1: J. Cannon, The recognition problem: What is a topological manifold? Bull. Amer. Math. Soc. 84 (1978), 832-866.
2: M. Freedman és F. Quinn, The topology of $4$ -manifolds, Princeton Math. Series 39, Princeton, NJ, 1990.
3: P. Teichner, Knots, von Neumann Signatures, and grope cobordism, Proceedings of the international congress of mathematicians, Vol H: Invited lectures, 2002, 437-446.

Megjegyzések

Peter Teichner a Berkeley California Egyetem matematika professzora. E-mail címe: Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.
A szerző köszönetet mond Ric Ancelnek a vizsgált fogalom eredetének tisztázásáért.

A fenti dolgozat eredetije 2004 szeptemberében jelent meg a Notices of the American Mathematical Society folyóiratban. Peter Teichner, WHAT IS...a Grope? Notices Amer. Math. Soc. Vol. 51 Num. 8 (September, 2004) 894-895. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. Fordította Kalmár Boldizsár.