Nézd és mondd!

Számsorozatok rengeteg matematikai mulatság tárgyát képezik. A hagyományosabbaktól (Fibonacci-sorozat — az első két szám 0 és 1, utána minden következő az előző kettő összege: 0, 1, 1, 2, 3, 5, 8, 13, 21 stb.) az egészen elborultakig (lusta pincér sorozat — $n$ számú vágással legfeljebb hány részre lehet szeletelni egy tortát: 1, 2, 4, 7, 11, 16, 22 stb.) Dunát lehet rekeszteni a különböző számsorozatokkal, a képzési lehetőségek végeláthatatlan volta miatt. 1964-ben egy Neil Sloane nevű matematikus elkezdte szisztematikusan gyűjteni az egész számokból álló számsorozatokat [6]. 1973-ban már több mint 2000-nél járt, 1995-ben elérte az 5000-et, mígnem 1996-ban egész projektjét feltöltötte az Internet-re, létrehozva az Számsorozatok Online Enciklopédiáját (OEIS, http://oeis.org/). Az OEIS-ben minden számsorozat egy egyedi azonosítóval rendelkezik, például a Fibonacci az A000045, a lusta pincér az A000124, és kommentárral, a számsorozatra vonatkozó tételekkel, őket generáló programmal stb. vannak ellátva. Az OEIS bővülési üteme egészen elképesztő, a 100 ezredik sorozatot 2004-ben, a 200 ezredik sorozatot 2011-ben adták hozzá; ma már több mint 250 ezer sorozatot tartalmaz. (Köztük azt, mely azokból az $n$ számokból áll, melyekre igaz, hogy az A $n$ azonosítójú OEIS sorozat tartalmazza $n$ -et: A053873-ös sorozat. Gondolatébresztő filozofikus kérdés: vajon az 53873 benne van az A053873-ös sorozatban?) Az OEIS messzemenőkig támogatja a közösségi bővítést: a meglevő számsorozatok kommentálhatóak, sőt, ha valaki talál egy sorozatot, amelyet újnak gondol, felajánlhatja nekik!

E sorozatok közül is kiemelkedik meghökkentő, sőt, helyenként egészen elképesztő tulajdonságai révén az a sorozat, melyet John Conway 1987-ben talált. (Conway számos egyéb szórakoztató matematikai konstrukció szerzője, az Életjáték nevű sejtautomatája például hazánkban is népszerűvé vált már 1970-es, 80-as években.)

1. Nézd és mondd

Conway sorozatának [1] képzési szabálya nagyon egyszerű: első tagja 1, az összes többit pedig úgy kapjuk, hogy kiolvassuk az előző tagot, és szó szerint leírjuk az ebben szereplő számokat. Például az 1 számot úgy olvassuk ki, hogy „1 darab 1-es”, így a sorozat második tagja: 11. Ennek kiolvasása: „2 darab 1-es”, így a következő tag 21. Ezt már úgy olvassuk ki, hogy „1 darab 2-es és 1 darab 1-es”, így a negyedik tag a 1211. És így tovább, a sorozat első néhány tagja:

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, 31131211131221.

(Remek fejtörő-feladvány e ponton megkérdezni gyanútlan ismerősünktől, akinek nem árultuk el a képzési szabályt, hogy vajon mi a sorozat következő tagja!)

Persze nem muszáj 1-ből indulnunk: kezdhetünk 2-vel (2, 12, 1112, 3112, 132112, 1113122112, 311311222112 stb.) 3-mal (3, 13, 1113, 3113, 132113, 1113122113, 311311222113 stb.), sőt, az indító szám nyugodtan lehet több számjegyű is (például 21, 1211, 111221, 312211, 13112221 stb.).

Conway ezt nevezte „look-and-say” (nézd és mondd, avagy: olvasd fel és írd le) sorozatnak. Az egészben az a legérdekesebb, hogy miközben a sorozat (nagyon) nem „matematikai” módszerrel van generálva, kiderült, hogy egészen mellbevágó — és igencsak matematikai eszközökkel leírható — tulajdonságai vannak.

2. És akkor megoldunk egy egyszerű 71-ed fokú egyenletet

Néhány tulajdonsága a sorozatoknak elég könnyen látható. Például: új 4-es vagy annál nagyobb számjegy nem keletkezhet a második tag után, hiszen mondjuk az 1111 azt jelentené, hogy az előző tag 11 volt, ami lehetetlen, mert ezt egybe kellett volna írni: „1 darab 1-es és 1 darab 1-es nincs”, az „2 darab 1-es” kellett volna legyen.

Ezzel együtt is érezhető, hogy annak nincs sok teteje, hogy a sorozat tagjait mint számokat tekintsük, de mi történik, ha azt vizsgáljuk, hogy az egyes tagok hány számjegyből állnak? A 22 végtelenül saját magát ismétli, ez tehát mindig 2 hosszú, de az összes többi esetben valami nagyon érdekes dologhoz jutunk; az 1. ábra mutat is erre pár példát.


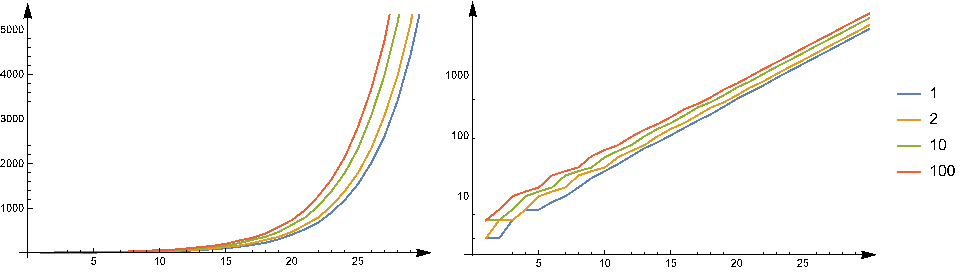
(a) Lineáris skálán	(b) Függőleges tengely logaritmikus
1. ábra: Sorozatok hosszának alakulása különböző kezdőértékekre

A számok hosszai tehát, nem túl meglepő módon, egyre nőnek — de nem akárhogy: exponenciális növekedést látunk, ráadásul nagyon hasonló mintájút! Ha a függőleges tengely skálázását logaritmikussá tesszük (1b. ábra), akkor egymással párhuzamos egyeneseket kapunk: el vannak tolva függőlegesen, de a meredekségük ugyanaz. Be lehet látni, hogy ez általánosságban is így van: az $n$ -edik tag hossza $C\lambda^n$ alakú, ahol $C$ minden kezdőszámra más, de a $\lambda$ ugyanaz! Ez más szóval azt jelenti, hogy ha elosztjuk egymással a sorozatok egymást követő tagjainak hosszát, akkor egy adott, állandó számhoz tartó sorozatot kapunk, ez lesz ez a bizonyos $\lambda$ (hiszen $C\lambda^{n+1}/C\lambda^n=\lambda$ ). Csakugyan, ha megnézzük például az 1 kezdőszámra, hogy hogyan alakul ez a hányados, akkor a 2. ábrán látható eredményt kapjuk.

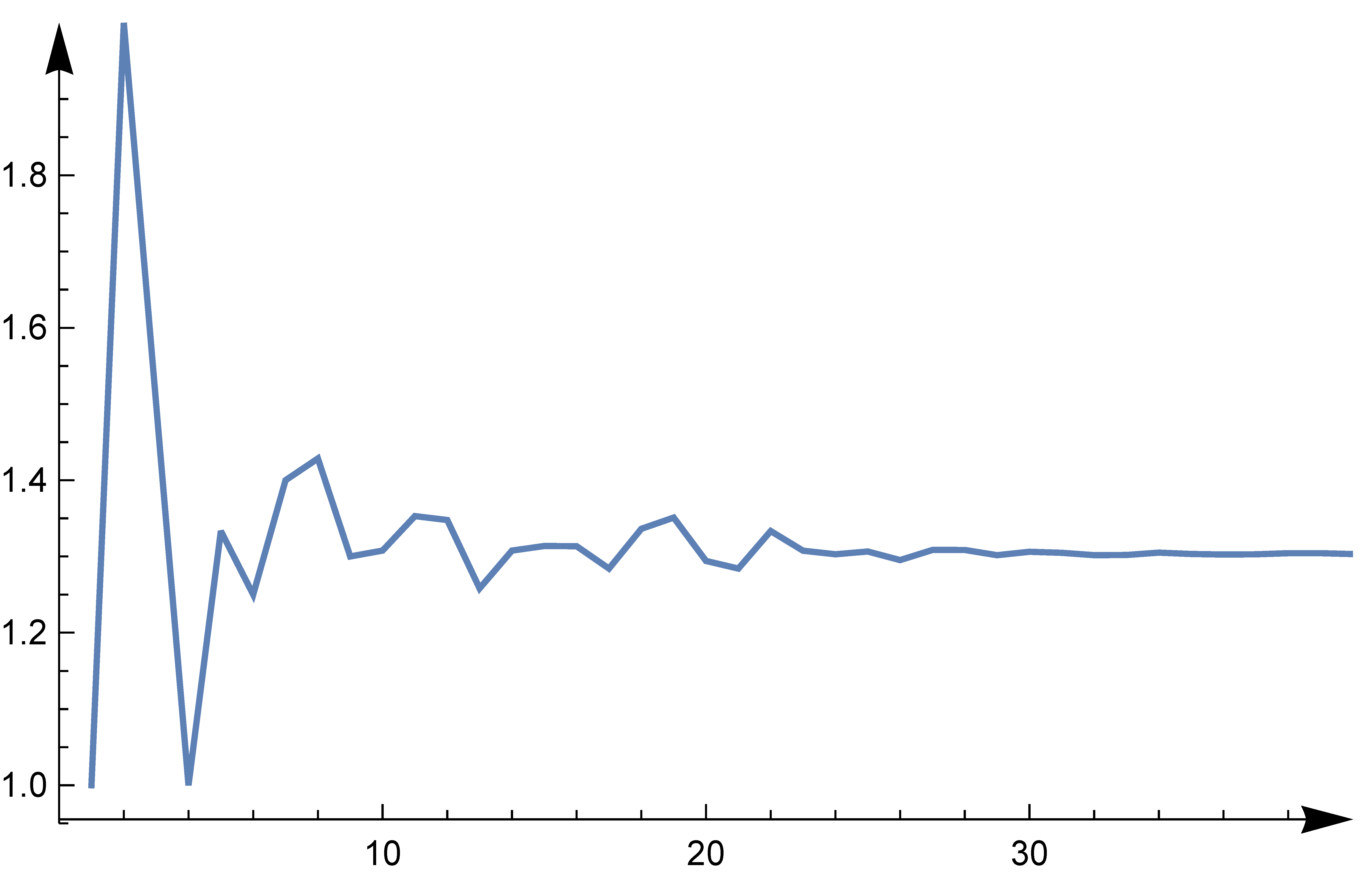
2. ábra. A sorozat egymást követő tagjai hosszának a hányadosa, ha az első szám 1

Jól látható, hogy a hányados valóban közelít egy adott számot, ez lesz a $\lambda$ . De vajon mennyi ennek az értéke? Conway bebizonyította [1], hogy ez nem más, mint a következő 71-ed fokú egyenlet egyetlen pozitív valós szám megoldása:

$\displaystyle x^{71}-x^{69}-2x^{68}-x^{67}+2x^{66}+\ldots-7x^{6}+7x^{5}-4x^{4}+12x^{3}-6x^{2}+3x-6=0.$

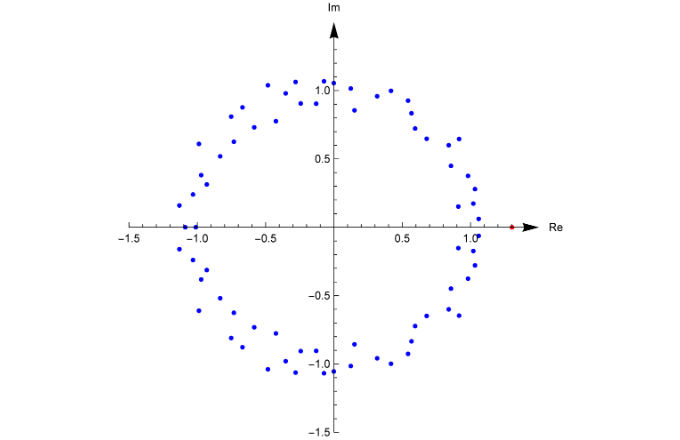
Az egyenlet — komplex — megoldásait a 3. ábra mutatja, pirossal kiemelve az említett egyetlen pozitív valós gyök. Nevezhetjük ezt Conway-állandónak is, értéke 10 tizedesjegy pontossággal: $\lambda=1{,}3035772690$ . Ez nem „közelítő'' eredmény vagy becslés: a fenti egyenlet egzaktan $\lambda$ -t szolgáltatja — ki gondolná, hogy a számok felolvasásával és leírásával kapott sorozat számjegyeinek növekedési ütemét pontosan megadja egy 71-ed fokú egyenlet?!

3. ábra. A Conway által megtalált 71-ed fokú egyenlet megoldásai a komplex számsíkon, piros kiemelés mutatja az egyetlen pozitív valós gyököt

3. Audioaktív bomlás

Conway tett egy fontos egyszerűsítő észrevételt is a számsorozatok képzésével kapcsolatban: bizonyos esetben egy hosszabb számsorozat felbontható két részre úgy, hogy az egyes részek „külön életet élnek”, olyan értelemben, hogy egymástól függetlenül vizsgálhatóak, ha a számsorozat további tagjaira vagyunk kíváncsiak. Tehát például ha kíváncsiak vagyunk, hogy egy XY alakú szám után 10-zel mi következik a számsorozatban, vagy, ahogy Conway fogalmazott: mi a 10. utódja XY-nak, akkor ezt megkaphatjuk úgy, hogy külön kiszámoljuk X 10. utódját és Y 10. utódját, majd a kettőt egész egyszerűen ilyen sorrendben egymás után írjuk. Azaz: nincs szükség a (hosszú) XY vizsgálatára, elég ha tudjuk, hogy a (rövid) X és Y hogyan viselkedik — a bonyolultabb probléma visszavezethető egyszerűbb problémákra. Ennek feltétele nyilván az, hogy X utódjai között egy olyan se legyen, melynek utolsó számjegye megegyezik Y ugyanazon sorszámú utódjának első számjegyével. Conway összeszedte az összes olyan esetet, amikor ez megtörténhet, példának okáért ilyen, ha X utolsó számjegye 4, Y-ban pedig nincs 4-es: ekkor a 4 szám mindig el fogja választani a két rész utódjait.

De mi van akkor, ha az X maga is szétbontható két részre? Ekkor még egyszerűbb az elemzés! És ha ezek a részek tovább bonthatóak...? Van ennek valahol határa? Azaz: léteznek olyan számok, amelyek már nem bonthatóak — a fenti értelemben — „elemibb” egységekre?

A válasz a kérdésre pozitív: léteznek olyan számok, amelyek tovább nem redukálhatóak a fenti módon; nevezzük az ilyen számokat atomnak, a több ilyenből felépülő számokat pedig az atomok által alkotott molekulának. Az igazán érdekes rész most jön: Conway felfedezte [1], hogy bár végtelen sok atom létezik, de van közöttük 92, ami igencsak megkülönböztetett szerepű, mindjárt látni is fogjuk, hogy miért.

92 atom? De hát pont ennyi a természetben előforduló atomok száma! (Legalábbis klasszikusan. Ma már tudjuk, hogy valójában a 43-as rendszámú technécium nem fordul elő a természetben, illetve a 93-98-as rendszámú elemek is előfordulnak, bár nagyon kis mennyiségben.) Conway el is nevezte ezeket a számokat: a hidrogén a 22, a hélium a 13112221133211322112211213322112, és így tovább, végezetül az urán a 3. Hogy teljes legyen az analógia, azt a műveletet, amikor egy számból „nézd és mondd” módon a következő számot származtatjuk, nevezzük bomlásnak. Conway ezzel megalkotta az „audioaktív” bomlást: számok lebomlását felolvasás alapján!

Mi a különleges ebben a 92 számban (atomban)? Először is, a bomlásuk zárt hálózatot alkot: a 92 szám mindegyike olyan számra bomlik, ami szintén benne van ebben a 92-ben. Ezt a hálózatot — matematikai szóval élve: gráfot — mutatja a 4. ábra, mely Mario Hilgemeiertől származik [4].

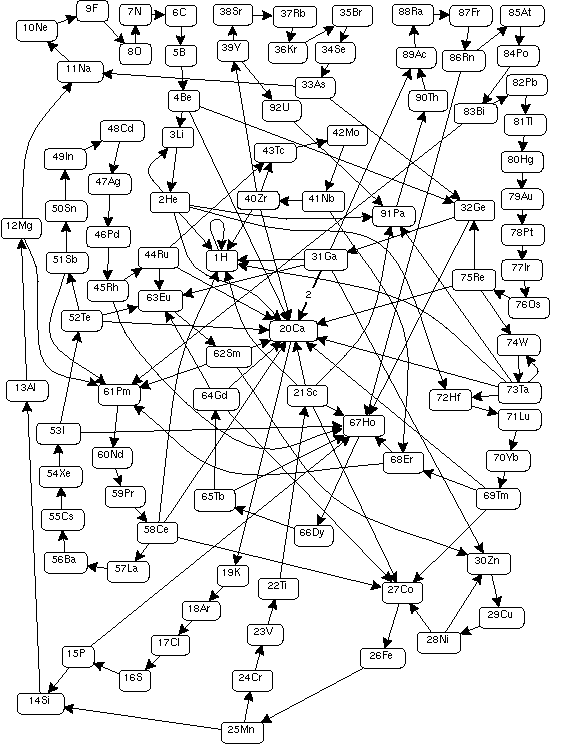
4. ábra. Az atomok bomlását mutató gráf

Például az 1-es jelű hidrogén, a 22 saját magára bomlik, ezért az önmagában mutató hurokél. A 2-es jelű hélium utódja egy olyan molekula, melyben van hidrogén, de még öt másik atom is (ellenőrizzük kézzel!), mindegyikbe mutat egy nyíl. És így tovább.

Az igazán elképesztő rész azonban még csak most jön.

4. Fermat után szabadon

Ahogy mondtam, végtelen sok atom van, így értelemszerűen a fenti 92 nem tartalmazza mindegyiket. Például, rögtön az 1-es nincsen benne. Azonban nézzük csak meg a „bomlási sorának” a hetedik tagját! 1113213211. Ha ezt összevetjük Conway táblázatával, akkor észrevesszük, hogy a 11132 épp a 72-es rendszámú hafnium, a 13211 pedig az 50-es rendszámú ón. Az 1-es bomlásakor tehát egy ponton „ón-hafnium” keletkezett — márpedig innentől kezdve a fentiek miatt valamennyi későbbi szám már szükségképp a 92 fenti atomból felépülő molekula kell legyen! Megnézve a gráfot, látjuk, hogy a hafnium a 71-es rendszámú lutéciumra (311312) bomlik, az ón pedig a 49-es rendszámú indiumra (11131221), márpedig ezek atomok, így egymástól függetlenül leszármaztathatóak. És valóban: ha visszalapozva megnézzük az 1 bomlási sorának következő „termékét”, akkor az tényleg a 31131211131221! (Íme az audoaktív kémia!) Hasonlóan végigkövethetőek a további lépések is.

És akkor jöjjön az elképesztő rész: Conway bebizonyította [1], hogy ez nem véletlen: előbb vagy utóbb mindegyik (!) kezdőszám olyan utódokat hoz létre, amiben ez a 92 atom fog szerepelni! Bármilyen számból is indítjuk a sort, egy ponton olyan szám fog létrejönni, ami kizárólag a 92 Conway által összegyűjtött számból — atomból — épül fel! Márpedig ha ez egyszer megtörténik, akkor a zártság miatt ez már az adott sorozat összes többi tagjára is igaz lesz. Ennek a pontnak az elérése ráadásul nem is igényel rengeteg lépést: Mike Guy igazolta, hogy legfeljebb 24 lépésen belül mindenképp elérjük a 92 atomból álló számokat, és ez a határ éles is, a 2233322211 $n$ szám esetén tényleg kell ennyi lépés, ahol $n$ tetszőleges 1-nél nagyobb szám.

Ezzel azonban még mindig nincs vége a meghökkentő eredményeknek. Tegyük fel, hogy származtatunk egy számot, majd az eredményt felbontjuk atomokra. Ezt megtéve, meghatározhatjuk az egyes atomok arányát; például az 1 hetedik leszármazottjában 50% ón és 50% hafnium van. A nyolcadikban 50% lutécium és 50% indium. Ha tovább megyünk, akkor egyre több és több elem fog megjelenni. Sőt, ennél jóval több is igaz: a hidrogén kivételével mindegyik atom — és így az előbbiek miatt mindegyik szám — bomlási sorában előbb vagy utóbb az összes elem megjelenik! Azaz: bejárjuk a teljes fenti gráfot. Természetesen az elemek aránya, mint az előbb is láttuk, folyamatosan változik, de megdöbbentő dolgot találunk, ha nagyon sok bomlási lépésen keresztül követjük nyomon az egyes atomok arányait: azt fogjuk észrevenni, hogy ezek nem össze-vissza ingadoznak, hanem egyre közelebb kerülnek egy adott értékhez, az ón esetében ez például 1,6 ezrelék. Ráadásul Conway azt is bebizonyította [1], hogy bármilyen számból indítjuk a sorozatot, az arányok mindig ugyanoda fognak tartani! Nyugodtan mondhatjuk tehát, hogy az atomok „előfordulási gyakorisága” egy pusztán rájuk jellemző állandó. A leggyakoribb elem a hidrogén, a 22 (9,2%), a legritkább az arzén, a 11131221131211322113322112 (27 per millió).

Ezen a ponton azt is elárulom, hogy egy kicsit csaltam a korábbi állítás megfogalmazásánál: valójában a 92 elemen kívül még előfordulhat több is a bomlási sorban, hosszú távon is (Conway a rá jellemző szellemességgel ezeket természetesen transzurán elemnek nevezte...), ám olyan értelemben „nem lényegesek”, hogy az előfordulási arányuk bizonyíthatóan a nullába tart.

A végére hagytam egy érdekes részt: e megállapítások — amit Conway egyébként „kozmológiai tételnek” nevezett el — bizonyításának történetét. Maga Conway az eredeti cikkben úgy jellemezte a problémát, hogy e tétel ,„bizonyítása ELKÉPESZTŐEN nehéz”; csupa nagybetűs kiemelés az eredetiben. Leírta, hogy több kollégájával együtt egy hónapon keresztül „igen megfeszített” munkával dolgozott a kérdésen, és sikerült is két bizonyítást adni, mindegyik több tucat oldalt töltött meg — csakhogy a lapokat elvesztették! (De legalább nem könyv margójára próbálták írni...)

Tíz éven keresztül senki nem is bizonyította a tételt, mígnem Shalosh B. Ekhad és Doron Zeilberger 1997-ben megadta a második — első fennmaradt... — bizonyítást [2]. (A két szerzőből csak Doron Zeilberger szerző a szó hagyományos értelmében: Shalosh B. Ekhad nem más mint Zeilberger számítógépe — az izraeli matematikus annyira elkötelezett híve a számítógépek matematikában történő alkalmazásának, hogy rendszeresen feltünteti társszerzőként „őt”, Shalosh B. Ekhad ugyanis annyit tesz héberül, hogy 3B1, ami Zeilberger első gépének a típusszáma [3].) E bizonyítás hátránya, hogy csak annyit támaszt alá, hogy 29 lépésen belül elérjük a 92 atom valamelyikét, tehát a 24 lépéses határt nem hozza. Erre sem kellett azonban sokáig várni: 2003-ban Richard Litherland újabb bizonyítást adott, mely immár a 24 lépéses határt is alátámasztotta [5]. E sorok szerzője még egy további bizonyításról tud, ez pedig Kevin Watkins-tól származik 2006-ból [7].

Valamennyi bizonyítás közös jellemzője, hogy a problémát visszavezeti bizonyos esetek egyesével történő leellenőrzésére; „apró” különbség, hogy ezt Conwayék kézzel tették meg, míg a későbbi megoldások számítógéppel. Zeilberger Maple-t használt, Litherland C-t, Watkins Haskell-t. E módszerek felvetik az általános problémát, hogy vajon mikor tekinthető egy ilyen számítógép-program eredménye a szó matematikai értelmében „bizonyítás”-nak, ahogy az ma már legendás módon a négyszín-sejtés bizonyítása kapcsán közismert kérdéssé vált — de ez már egy másik írás témája lehetne.

Ferenci Tamás

Élettani Szabályozások Kutatóközpont, Óbudai Egyetem

Irodalomjegyzék

1: J. H. Conway. The weird and wonderful chemistry of audioactive decay.
In Thomas M. Cover and B. Gopinath, editors, Open Problems in Communication and Computation, pages 173—188. Springer New York, New York, NY, 1987.
2: Shalosh B. Ekhad and Doron Zeilberger. Proof of Conway’s lost cosmological theorem.
Electronic Research Announcements of the American Mathematical Society, 3(11):78—82, 1997.
3: Joe Gallian and Michael Pearson. An interview with Doron Zeilberger.
FOCUS, 27(5):14—17, 2007.
4: Mario Hilgemeier. ,,one metaphor fits all'': A fractal voyage with Donway's audioactive decay.
In Clifford Pickover, editor, Fractal horizons: The future use of fractals, chapter 7. St. Martin's Press, New York, 1996.
5: Richard A Litherland. Conway’s cosmological theorem. https://www.math.lsu.edu/~lither/jhc/cct.pdf, 2003.
6: N. J. A. Sloane. The on-line encyclopedia of integer sequences.
AMS Notices, 50:912—915, 9 2003.
7: Kevin Watkins. Abstract interpretation using laziness: Proving Conway’s lost cosmological theorem.
http://www.cs.cmu.edu/~kw/pubs/conway.pdf, 2006.