Rendszerint gyanakodva fogadom, amikor valaki arról beszél, hogy nem ment neki a matek. Lehet, hogy nagyon is jól ment – volna, csak nem úgy mondták el neki, ahogy ő be tudta volna fogadni. Esetleg benne ragadt egy kérdés még az elején, amire senkitől nem kapott választ. Talán meg sem tudta jól fogalmazni a problémáját, mégis elvesztette emiatt a bizalmát és az érdeklődését. Vagy – szoktam ilyenkor gondolni – az illető igazából nem is találkozott még matematikával. Amivel találkozott az iskolában, azt nem nevezném annak. A japán rajzfilmkészítő, Takahata Iszao Yesterday – Vissza a gyerekkorba című animációs filmjének egyik jelenetében nagyon tanulságos példát láthatunk erre a jelenségre (1:04:10-nél kezdődik).
A film főhősének, Taekonak ötödikes korában nem ment a törtek osztása. Rossz dolgozatot írt belőle, és az édesanyja a nővéréhez küldte őt korrepetálásra. Hamar kiderült, hogy Taeko is tudja, hogyan kellene kiszámolni a helyes eredményt, de nem érti, mi ennek a jelentése. Pontosabban amire ő gondol, az más eredményt ad, és emiatt össze van zavarodva.
„Mi az egyáltalán, hogy törtet osztunk törttel?” – kérdezi Taeko a nővérét. Az ő eszmefuttatása szerint  -ot elosztani
-ot elosztani 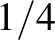 -del azt jelentené, hogy 4 felé osztjuk, tehát
-del azt jelentené, hogy 4 felé osztjuk, tehát 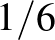 -ot kapunk. A nővére nagyon helyesen rámutat, hogy így nem osztott, hanem szorzott
-ot kapunk. A nővére nagyon helyesen rámutat, hogy így nem osztott, hanem szorzott 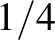 -del, de Taeko számára ez újabb ellentmondást okoz: „Hogy lenne kisebb, ha szorzok?” A nővére próbál belegondolni az
-del, de Taeko számára ez újabb ellentmondást okoz: „Hogy lenne kisebb, ha szorzok?” A nővére próbál belegondolni az 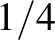 -del való osztás jelentésébe, sikertelenül, majd elhangzik az a mondat, ami talán egész életére meghatározza Taeko viszonyát a matematikához: „Nem ez a lényeg. Verd ki a fejedből az almákat! Csak megcseréled, aztán pedig megszorzod, ezzel törődj!”
-del való osztás jelentésébe, sikertelenül, majd elhangzik az a mondat, ami talán egész életére meghatározza Taeko viszonyát a matematikához: „Nem ez a lényeg. Verd ki a fejedből az almákat! Csak megcseréled, aztán pedig megszorzod, ezzel törődj!”

A  négy részre osztása Takahata Iszao: Vissza a gyerekkorba című animációs filmjében, amit a főhős, Taeko
négy részre osztása Takahata Iszao: Vissza a gyerekkorba című animációs filmjében, amit a főhős, Taeko 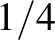 -del való osztásnak gondol – pedig valójában szorzás
-del való osztásnak gondol – pedig valójában szorzás 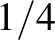 -del.
-del.
Akkor végülis tényleg nem ment a törtek osztása Taekonak? Ő is ki tudta – volna – számolni ugyanúgy, mint a nővére. Csak nem volt hajlandó ész nélkül alkalmazni egy receptet, aminek nem látja az értelmét. Nem volt butább a többieknél, sőt, talán matekosabb gondolkodásra vall, hogy meg is akarja érteni, amit csinál. De ebben a megértésben senki nem tudott segíteni neki. Volt egy elakadása, amin aztán nem tudott továbblendülni, úgy maradt, rossz matekos lett.
Vajon hányan ülhetnek hasonló tapasztalattal az iskolapadokban, és mennyien lehetnek a felnőttek között, akiket elkönyveltek rossz matekosnak, pedig csak gondolkodtak, nem látták értelmét, és nem kaptak segítséget? Úgy képzelem, hogy ez egész általános jelenség lehet: ha valaki nem matekzseni, hogy magától rájöjjön, vagy legalább nagyon precíz kérdést fogalmazzon meg, de közben gondolkozik, keresi az értelmét az iskolában tanultaknak, akkor szükségszerűen belebotlik ehhez hasonló kérdésekbe – és kétséges, hogy talál-e valakit, aki ezeken átsegíti őt.
Én saját élményként is jól ismerem ezt a fajta elakadást, igaz, leginkább nem általános iskolából, hanem a kutatói munkámból. De attól még ugyanolyan frusztráló, sőt! Egyre kevesebb ember van a bolygón, akivel az ilyen elakadásokat részletesen át tudom rágni, hiszen ehhez kell az, hogy nagy tudása legyen az adott témáról, és rám szánja a figyelmét, hogy megértse, hogy én mit nem értek. Másrészt pedig egész tudományágak is működnek hasonló elakadásban. Például a kvantummechanika értelmezésével kapcsolatban csak félig viccesnek szánt szállóige, hogy „Fogd be a szád, és számolj!”
De térjünk vissza Taekohoz. Mit válaszolnánk neki, hogyan magyaráznánk el a törtek osztását? Ha hozzám fordulna Taeko ezzel a problémával, előszöris a törtek szorzását tisztáznám vele. A magyar nyelv kicsit félrevezető ez ügyben (bár a japánt nem tudom). Valamit elnegyedelni annyit tesz, mint négy egyenlő részre osztani, így amit ő lerajzolt, az a  osztva 4-gyel, a
osztva 4-gyel, a  negyed része, vagy ha úgy tetszik, a
negyed része, vagy ha úgy tetszik, a  egy negyede. Ez az
egy negyede. Ez az 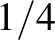 -de való szorzás:
-de való szorzás:
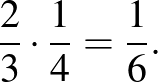
Igen, megszoroztam és kisebb lett, mert 1-nél kisebb számmal szoroztam – ezen el lehet tűnődni más péládák kapcsán is. De a negyedelés miért 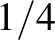 -del való szorzást jelent? Ez számomra úgy lesz igazán meggyőző, hogyha egész számot szorzok
-del való szorzást jelent? Ez számomra úgy lesz igazán meggyőző, hogyha egész számot szorzok 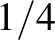 -del, például
-del, például 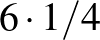 , és fordítva tekintem: a 6-tal szorzom meg az
, és fordítva tekintem: a 6-tal szorzom meg az 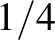 -et, azaz 6-szor összeadom önmagával:
-et, azaz 6-szor összeadom önmagával:
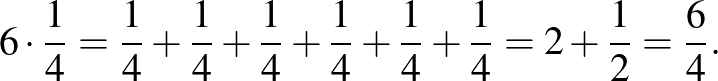
Összefoglalva: a törttel való szorzás a törtrész kiszámítása. Ez a legalapvetőbb gondolat nem nyilvánvaló, inkább meglepő.
Most jöhet az osztás! Valóban elakadunk már az elején: mit jelent az, hogy a  -ot
-ot 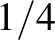 darab egyenló részre osztom? Nem azt, amit Taeko rajzolt, mert az a 4-gyel való osztás, azaz
darab egyenló részre osztom? Nem azt, amit Taeko rajzolt, mert az a 4-gyel való osztás, azaz 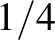 -del szorzás. Tudjuk, hogy mit nem jelent, de attól még nem tudjuk, hogy mit jelent. Lépjünk hát egyet hátra! Nézzünk olyan példát, amiben tudjuk az osztás jelentését, mondjuk, 12 osztva 3-mal (
-del szorzás. Tudjuk, hogy mit nem jelent, de attól még nem tudjuk, hogy mit jelent. Lépjünk hát egyet hátra! Nézzünk olyan példát, amiben tudjuk az osztás jelentését, mondjuk, 12 osztva 3-mal (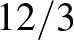 ). 12 ember belép az étterembe, őket kell 3 egyenlő csoportra osztani, vagyis 3 asztalhoz leültetni. Így egy-egy asztalnál 4 ember fog ülni.
). 12 ember belép az étterembe, őket kell 3 egyenlő csoportra osztani, vagyis 3 asztalhoz leültetni. Így egy-egy asztalnál 4 ember fog ülni.
De van ennek egy másik jelentése is! 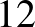 -ben a 3 (azaz
-ben a 3 (azaz 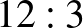 ) azt jelenti, hogy 3-mas csoportokat alkotunk a 12 emberből, azaz 3 fős asztalokhoz ültetjük le az embereket. Így összesen 4 csoport keletlkezik, 4 asztalt fognak elfoglalni. Az eredmény,
) azt jelenti, hogy 3-mas csoportokat alkotunk a 12 emberből, azaz 3 fős asztalokhoz ültetjük le az embereket. Így összesen 4 csoport keletlkezik, 4 asztalt fognak elfoglalni. Az eredmény, 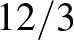 vagy
vagy 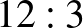 mindenképpen 4, de más a jelentése. Ezt az második féle jelentést szokás bennfoglalásnak hívni, és ezt jelöli a kettőspont.
mindenképpen 4, de más a jelentése. Ezt az második féle jelentést szokás bennfoglalásnak hívni, és ezt jelöli a kettőspont.

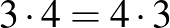
A bennfoglalás az általános iskolás matematika tananyag egyik legbizarrabb eleme, ekkor szoktak a szülők tömegesen reklamálni, hogy nem értik, amit a másodikos gyerekük tanul. Igen, mert a bennfoglalás ugyanaz, mint az osztás, pontosabban más a jelentése, de ugyanaz az eredménye. Valójában a különbség a kétféle szorzásból adódik: 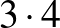 jelentése az, hogy
jelentése az, hogy 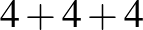 , míg a
, míg a 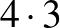 azt jelenti, hogy
azt jelenti, hogy  . Különböző a jelentés, de az eredmény ugyanaz.
. Különböző a jelentés, de az eredmény ugyanaz.
És most már válaszolhatunk Taekonak és a nővérének. A 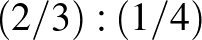 műveletet nem tudjuk osztásként értelmezni, hiszen nem tudunk
műveletet nem tudjuk osztásként értelmezni, hiszen nem tudunk 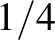 darab csoportot képezni a
darab csoportot képezni a  -ből. Az osztás első féle jelentése tehát ebben az esetben nem működik. Működik viszont a bennfoglalás: hányszor van meg
-ből. Az osztás első féle jelentése tehát ebben az esetben nem működik. Működik viszont a bennfoglalás: hányszor van meg  -ban az
-ban az 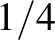 ? Taeko rajzán belemérhetjük az egésznek a
? Taeko rajzán belemérhetjük az egésznek a  részébe az
részébe az 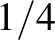 részét: belefér kétszer, meg még maradt egy pici. Ez a fennmaradó rész az
részét: belefér kétszer, meg még maradt egy pici. Ez a fennmaradó rész az 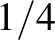 -nek a
-nek a  része, azaz
része, azaz  -szorosa. Tehát az
-szorosa. Tehát az 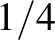 a
a  -ba belefér
-ba belefér 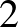 -szer és még
-szer és még  -szor. Azaz
-szor. Azaz
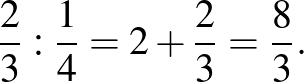
Tényleg ugyanaz, mint a reciprokkal való szorzás eredménye – a recept alkalmazása:
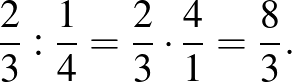
Megvan tehát, hogy mi a törttel való osztás jelentése. Igazából törttel való bennfoglalásnak kellene hívni, ha ehhez a szóhoz nem kapcsolódna egy 5. osztályra talán már sikeresen elnyomott trauma. Azt is látjuk a példán, hogy működik a recept. Legalábbis helyes eredményt ad, de egyelőre nem nyilvánvaló belőle, hogy ennek mindig így kell lennie.
Van másik módszer is, ahogy a törttel való osztást származtathatjuk, csak az sokkal formálisabb. E szerint az 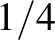 -del való osztás eredménye olyan szám, amit
-del való osztás eredménye olyan szám, amit 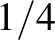 -del szorozva megkapjuk azt a számot, amit elosztottunk. Azaz – általánosan:
-del szorozva megkapjuk azt a számot, amit elosztottunk. Azaz – általánosan:
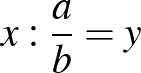 , ha
, ha 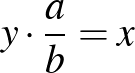 .
.
Ez a magyarázat Taeko számára nem volna kielégítő, hiszen nem derül ki belőle, mit jelent ez a művelet az almák darabolására vonatkoztatva. Viszont a jól ismert reciprok-recept kiolvasható belőle:
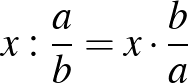 , hiszen
, hiszen 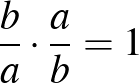 , és ezért
, és ezért 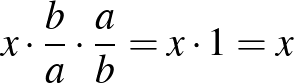 .
.
Látjuk, hogy egy matematikai fogalomnak nemcsak egyféle jelentése van, hanem különböző jelentésrétegei. Továbbá a megértés szubjektív dolog, mindenkinek mást jelenthet:

 -ban az
-ban az 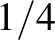
(1) A recept alkalmazása: Taeko nővérének az volt a megértés, hogy tudja a receptet, tudja, hogyan kell kiszámolni. Biztos vannak olyan diákok, akiket nem érdekel mélyebben a dolog, megelégszenek ezzel. Ilyen esetben jó célja a tanításnak, hogy gyakoroltassuk be velük a receptet, hogy tudják használni. De érdemes tudni, hogy lehetnek olyan diákok, akiket éppen ezzel veszítünk el, ráadásul ők azok, akiket érdekelne is a matek. Nekik mondanám azt felnőtt korukban, hogy igazából nem találkoztak matematikával. Mert ami nem ment nekik, az nem az volt, hanem gépies számolás.
(2) A matematikai megértés: A matematikai formalizmus számára a megértés az, hogy az osztás eredményét (a hányadost) visszaszorozva az osztóval kijön az eredeti szám (az osztandó). Ebből az elvből azonnal következik a recept, ezért a megértésnek ezen a szintjén mozogni kényelmes és rendkívül gyümölcsöző. A matematika javarészt ezen a szinten mozog. De ez a szint nem foglalkozik a világi (matematikán kívüli) jelentéssel.
(3) Világi megértés: Visszatérni a törtek (egyik) jelentéséhez, és az almákon elvégezni az 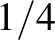 -del való osztás matematikai műveletét jóval nehezebb feladat, egyáltalán nem magától értetődő. A megértésnek ezen a szintjén nem véd meg a matematika, kiléptünk annak biztonságot adó formalizmusából, és bele kell gondolnunk a valóságba. Taeko azért került nehéz helyzetbe, mert a megértésnek ezt a szintjét igényelte (volna).
-del való osztás matematikai műveletét jóval nehezebb feladat, egyáltalán nem magától értetődő. A megértésnek ezen a szintjén nem véd meg a matematika, kiléptünk annak biztonságot adó formalizmusából, és bele kell gondolnunk a valóságba. Taeko azért került nehéz helyzetbe, mert a megértésnek ezt a szintjét igényelte (volna).
Az is kiderül ebből, hogy mindenki a személyes igénye szerint képes a megértésre, a más szinteken érkező magyarázatok nem működnek nála. Taeko nővérének hiába mutogatnánk a kördiagramot, hiszen ő megelégedett a recepttel, míg Taekonak a recept önmagában semmitmondó, csak kérdéseket vet fel. Ráadásul a törtek osztásának tényleges jelentése nem egy könnyű gondolat, ezért egyáltalán nem nyilvánvaló, hogy melyik módon érdemes bevezetni a témát.1
Ez tehát rossz hírnek tűnhet az oktatás számára: nincsen mindenki számára kielégítő magyarázat. Jó hír viszont, hogy minden értelmezhető sokféle módon, mindenkinek juthat az osztályban személyre szabott megértés, ami a többiekét is teljesebbé teszi. Ehhez „csak” az kell, hogy megértsük, hogy ki hogyan nem érti.
A matematikai fogalmak esetén minden alkalmazás új jelentésrétegeket nyit meg. Minden új alkalmazás új megértés és új ábrázolás is egyúttal. Most erre nézünk egy példát a törtek osztása esetén. Ez a példa elsőre nem segíti a törtekkel végzett műveletek megértését, hiszen még azt a területet is meg kell hozzá érteni, ahonnan a példa származik, ami jelen esetben a zene lesz. Ezt követően azonban mégis egy új színfoltot ad a történek osztásához.
Tehát ahogy említettem, a törtek szorzása és osztása nagyon szépen megjelenik a zenében, ha egy húr rezgéseit vizsgáljuk. A teljes sztorit el lehet olvasni Székely Péter cikkében vagy az én könyvemben, itt csak az idevágó gondolatot foglalom össze.
Minden tört – arány – egy adott hangköznek felel meg: ha olyan arányban fogom le a húrt, mennyivel lesz magasabb a hangja a húr alaphangjánál. Péládul ha egy húrt lefogunk a felénél, éppen egy oktávval magasabb hang szólal meg, mintha az eredeti húrt pengetnénk. A negyedénél lefogva (a negyedét pengetve) két oktávval magasabb hangot hallunk, a nyolcadát pengetve három oktávval magasabb és így tovább. A  -nak megfelelő hangköz a kvint: a húr hosszának
-nak megfelelő hangköz a kvint: a húr hosszának  -át pengetve a húr alaphangjánál egy kvinttel magasabb hangot hallunk. 2
-át pengetve a húr alaphangjánál egy kvinttel magasabb hangot hallunk. 2

Az oktávhoz a felénél, a kvinthez a  -nál kell lefogni a húrt.
-nál kell lefogni a húrt.
Milyen arány felel meg a kvint kiegészítő hangközének, a kvartnak? Azaz az oktávnál egy kvinttel mélyebb hang milyen aránynak felel meg az alaphanghoz képest? A kvinttel magasabb hang a  -dal való szorzás, tehát ha kvinttel mélyebb hangot szeretnék, akkor osztani kell
-dal való szorzás, tehát ha kvinttel mélyebb hangot szeretnék, akkor osztani kell  -dal. Mivel az oktáv az eredeti húrhossz
-dal. Mivel az oktáv az eredeti húrhossz 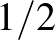 -szerese, ezért az oktávnál egy kvinttel mélyebb hangnak a
-szerese, ezért az oktávnál egy kvinttel mélyebb hangnak a
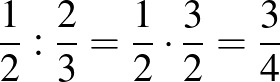
arány felel meg, azaz a húr 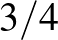 -ét kell pengetni ahhoz, hogy az alaphangnál egy kvarttal magasabb hangot kapjunk. Tehát az a zenei formula, hogy
-ét kell pengetni ahhoz, hogy az alaphangnál egy kvarttal magasabb hangot kapjunk. Tehát az a zenei formula, hogy
kvint + kvart = oktáv,
így fordítható le matematikára:
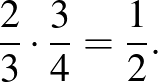
És most érdemes megvizsgálni a számolás jelentését a világi szinten is! Ha a húr 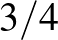 -ének veszem a
-ének veszem a  -át, az 2 darab negyed lesz, vagyis a húr fele. Fordítva, ha a
-át, az 2 darab negyed lesz, vagyis a húr fele. Fordítva, ha a  -nak veszem a
-nak veszem a 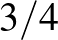 -ét: ehhez érdemes hatodokra bontani, mint Taeko az almát. A
-ét: ehhez érdemes hatodokra bontani, mint Taeko az almát. A  egy negyede
egy negyede 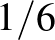 , tehát a három negyede
, tehát a három negyede 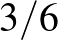 , azaz
, azaz 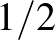 .
.

A kvint és a kvart oktávra egészítik ki egymást.
Arra szeretném tehát felhívni a figyelmet, hogy egy-egy matekos témának (is) ezernyi arca van, és mindenki más irányból érkezik a megértéshez, és más irányból akad el. Az elakadás végzetes is lehet egy ennyire egymásra épülő tudományban, mint a matek, egész életre elvághatja a diákot a matematikától és mindentől, ami arra épül. Ha ezt elfogadjuk, és figyelembe is akarjuk venni az oktatásban, nem tudok jobb módszert javasolni, mint a kétirányú kommunikációt a tanár és a diákok között. Ijesztően hangzik, hiszen rengeteg diák van, kevés idő, sok tananyag. De valójában, ha sikerülne átsegíteni egymást a személyes elakadásokon, azzal rengeteg extra erőfeszítést (munkát, időt) spórolnánk meg, mindenki jobb kedvvel és lelkesebben tanulna, dolgozna. És mivel mindenkinek másmilyen a megértése és az elakadása, a diákok igazából egymásnak tudnának a legtöbbet segíteni. Idealistán hangzik? Véleményem szerint akkor is ez az igazság.
Az ELTE matematikus szakán sikerült egy ilyen idilli rendszerben tanulnunk, együtt az évfolyamtársaimmal és a tanárainkkal a közös ügyért. Ez semmi máshoz nem fogható élmény. Ha szerencsém van, a különféle alkalmazások és kapcsolatok varázslatos színfoltjai egész életemen keresztül színezni fogják a világomat.
Lábjegyzetek
- 1 A magyarországi matematikatanítás hagyományosan felfedeztető jellegű, a tananyag spirális felépítésű. Ezért ha jól tanítjuk a matematikát, akkor a gyerekekben sok matematikai kép, modell előbb alakul ki (nem verbálisan), mint ahogyan azt a tanterv elvárja. Ez az értelmezés előkészítő szakasza. A tankönyvekben is ez köszön vissza (lásd https://www.tankonyvkatalogus.hu/pdf/OH-MAT06TA__teljes.pdf 54–76. oldal, https://www.tankonyvkatalogus.hu/pdf/OH-MAT06TB__teljes.pdf 149–178. oldal). Nagy hangsúlyt igyekszünk fektetni a tapasztalatszerzésre, ami lehetőséget teremt a gyerekeknek arra, hogy a saját elképzeléseik szerint építsék fel magukban a megértéshez szükséges szemléletet. Ilyen előkészületek esetén sokkal nagyobb az esély rá, hogy a tanulók megértik a törtekkel végzett műveleteket. Könnyen elképzelhető viszont, hogy idővel csak a szabályra emlékeznek, és nem fogják feltétlenül az értelmet keresni mögötte. Az, hogy természetes módon tudják elvégezni a műveleteket a törtekkel (anélkül, hogy újra és újra végig kelljen gondolniuk az értelmezésen alapuló hátteret), az absztrakció egy magasabb szintjét jelenti. (Szerkesztői megjegyzés.)
- 2 A hangközök zenei elnevezései (oktáv, kvint, kvart, …) a mi szempontunkból félrevezetőek, mivel másfajta rendszerből származnak. A hangoknak a zongora billentyűzetén elfoglalt helyét jelölik, és semmi közük a felhangrendszerbeli jelentéshez. Például a kvint jelentése öt(ödik), ennek semmi köze nincs a
 -hoz, mint ahogy az oktávnak (nyolc(adik)) sincs köze az
-hoz, mint ahogy az oktávnak (nyolc(adik)) sincs köze az 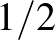 -hez. A kétféle megközelítés persze egy adott ponton találkozik, ezt a prímszámokról szóló könyvemben végigvezetem, de Székely Péter cikke is támpontot adhat.
-hez. A kétféle megközelítés persze egy adott ponton találkozik, ezt a prímszámokról szóló könyvemben végigvezetem, de Székely Péter cikke is támpontot adhat.
Pintér Gergő, BME Elméleti Fizika Tanszék











