Tisztelgés három nagy matematikus előtt

Egy pályázat története

Napjainkban a digitális tartalmak elképesztő mennyiségben jelen vannak az életünkben. Az utóbbi 10 évben a matematika területén belül is megindult a digitális ismeretterjesztés folyamata. Ennek egyik legjobban ismert alakja Grant Sanderson, avagy a 3Blue1Brown nevű YouTube-csatorna indítója. Ő csapatával együtt minden nyáron meghirdeti a Summer of Math Exposition nevű pályázatot, amelynek célja, hogy több matematikával foglalkozó tartalom legyen elérhető az interneten. Az első alkalommal, 2021-ben nagy sikert aratott a pályázat, ennek keretében több ezer színvonalas videó és más digitális tartalom készült. Mi, az Óbudai Árpád Gimnázium 12.b speciális matematika tagozatos osztály tanulói úgy döntöttünk – mivel érdeklődünk a matematika iránt és szívesen foglalkozunk különböző matematikával kapcsolatos témákkal –, hogy 2022 nyarán mi is részt veszünk ezen a pályázaton. Végül úgy határoztunk, hogy egy videót fogunk készíteni. Ezt a cikket azért írtuk meg, hogy motiváljuk a matematika iránt érdeklődőket arra, hogy az őket érdeklő témákban elmélyítsék és megosszák tudásukat.

Úgy gondoltuk, hogy kevés magyar csapat fog indulni a pályázaton, ezért szerettünk volna kifejezetten magyar vonatkozású videót készíteni. Tanárunk, Kézér Ildikó segítségével elkezdtünk olyan témákat keresni, amelyek nemcsak érdekesek, hanem gazdag vizualitással is rendelkeznek. Végül az Erdős–Szőkefalvi-Nagy-tétel mellett döntöttünk, hiszen Erdős Pál Magyarország legelismertebb matematikusa, és Szőkefalvi-Nagy Béla is a magyar matematika egyik legnagyobb alakja.

A tétel szerint bármely egyszerű konkáv sokszöget véges számú átfordítással konvexszé lehet tenni. Az átfordítás olyan transzformáció, amelyben a sokszög két kiválaszott csúcsa közötti pontokat a két csúcs által meghatározott egyenesre tükrözzük. Egy átfordítás csak akkor megengedett, ha a tükörtengely tartalmazza a sokszög konvex burkának egy szakaszát, különben az átfordított sokszög metszhetné önmagát. A konvex burkot szemléletesen úgy kaphatjuk meg, hogy egy befőttesgumit húzunk a sokszögre.

A bizonyításnak itt és az általunk készített videóban is szemléletes, egyszerűsített változatát mutatjuk be.

Mivel a tengelyes tükrözés távolságtartó transzformáció, egy átfordítás után a sokszög kerülete nem változik. Másrészt az átfordított csúcsok az összes belső ponttól távolodnak. Ez a háromszög-egyenlőtlenségből következik, mint ahogy az a képen is jól látható.

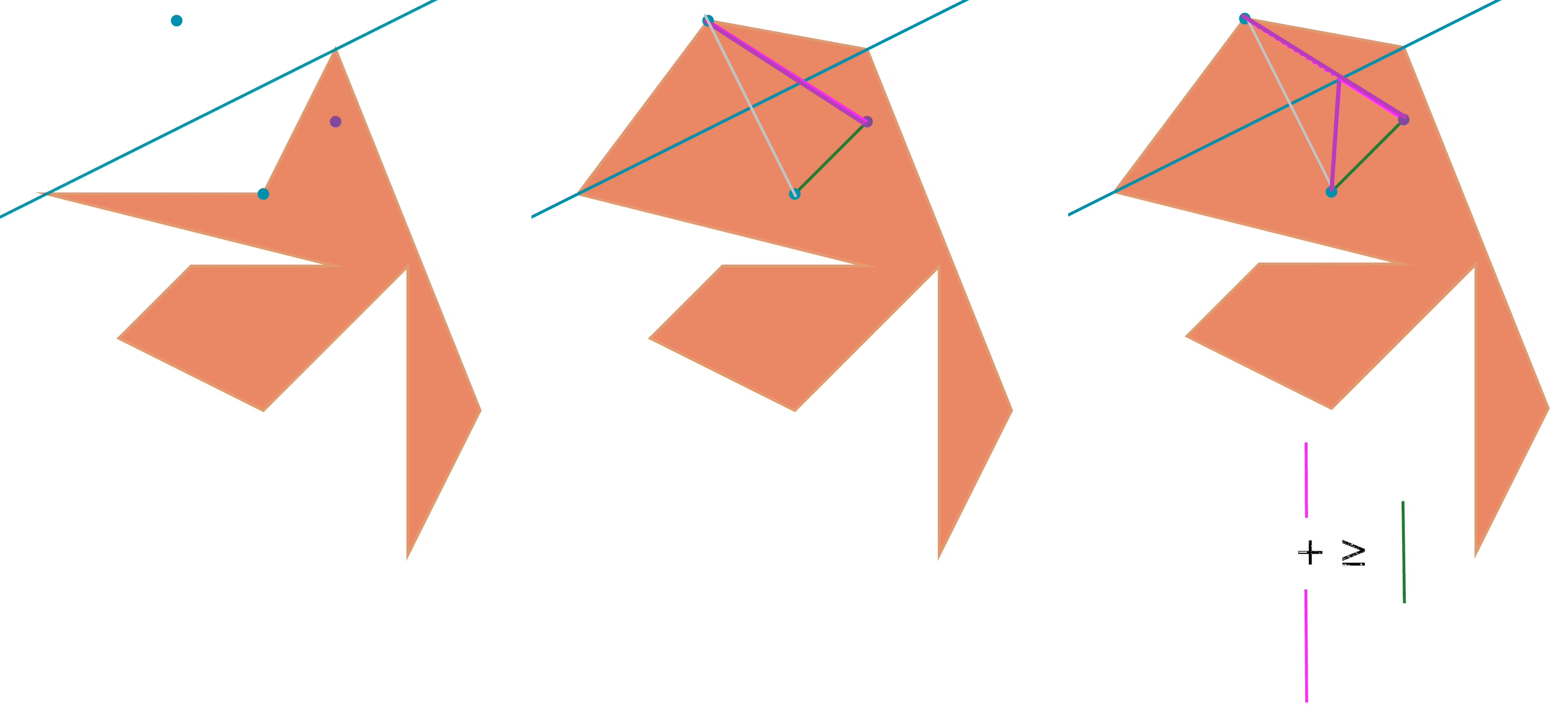
Vegyük észre, hogy bármely 2 belső pont távolsága kisebb, mint a kerület fele. Ezt az alábbi ábrán szemléltettük:

Az átfordítások során tehát a pontok egymástól mért távolsága monoton nő, és semelyik 2 pont nem lehet a félkerületnél nagyobb távolságra. Ebből az következik, hogy a sokszög bármely csúcsának az átfordítások során adódó képei egy konvergens pontsorozat részei, azaz a csúcsok helyének létezik határértéke. (Ennek az állításnak a bizonyítását a videóban tárgyaljuk részletesebben.)

Definiáljuk az eredeti konkáv sokszög határsokszögét úgy, mint az eredeti sokszöget alkotó csúcsok határhelyzetei által alkotott sokszöget. A határsokszög biztosan konvex, hiszen ha nem lenne az, akkor tudnánk még átfordításokat végrehajtani. Ez azt jelenti, hogy végtelen sok lépésen belül konvexszé tudunk tenni bármilyen egyszerű konkáv sokszöget. Ahhoz, hogy belássuk, hogy ezt véges sok lépésben is meg tudjuk tenni, fel kell használnunk a konvex sokszögek egy tulajdonságát, az úgynevezett konvexitási toleranciát. Tekintsük egy konvex sokszög tetszőleges 3 szomszédos csúcsát. Vegyük fel a csúcsok mint középpont köré az őket összekötő oldalak felezési pontjai által meghatározott egyenest érintő köröket.

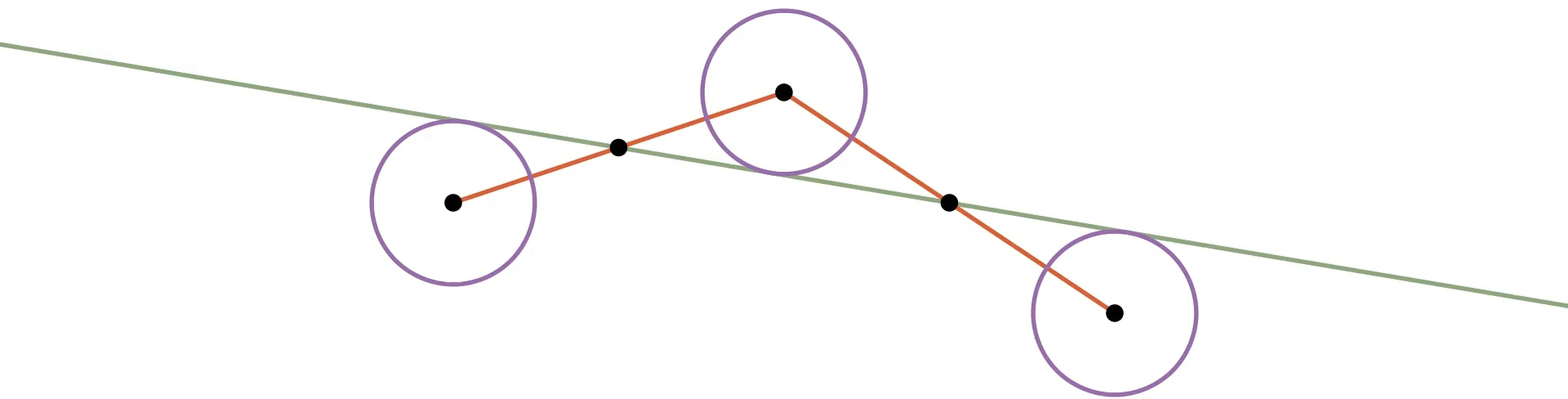
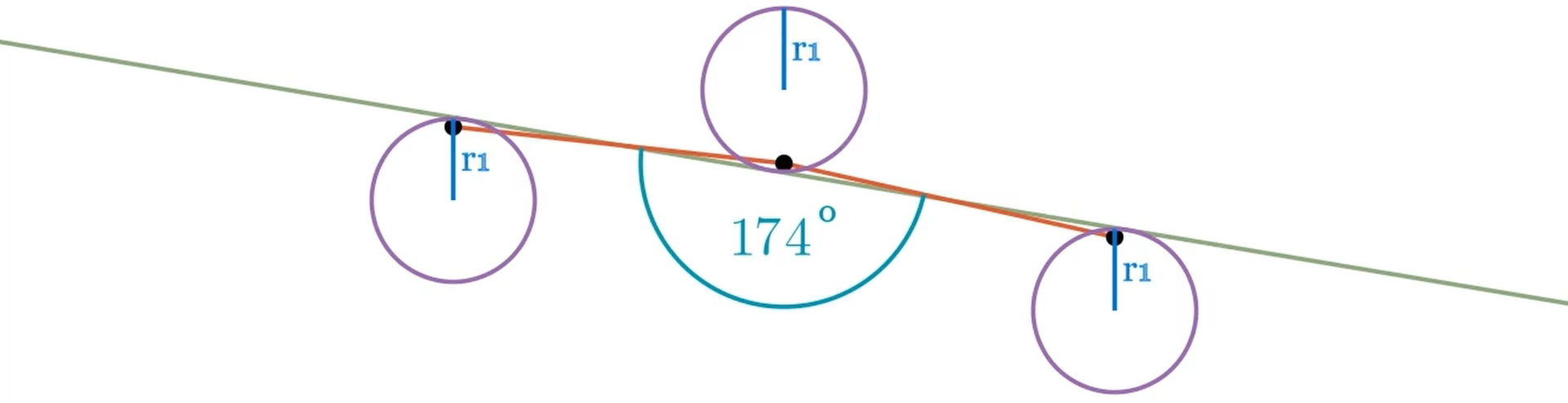
Ha ezt az összes lehetséges szomszédos ponthármasra elvégezzük, majd a kapott körök sugarai közül kiválasztjuk a legkisebbet, akkor megkapjuk a sokszög konvexitási toleranciáját. Ha ezzel a sugárral minden csúcs mint középpont köré kört szerkesztünk, a csúcsokat ezeken a körökön belül tetszőlegesen mozgatva a sokszög minden belső szöge, így a sokszög is konvex marad (ld. a videóban).

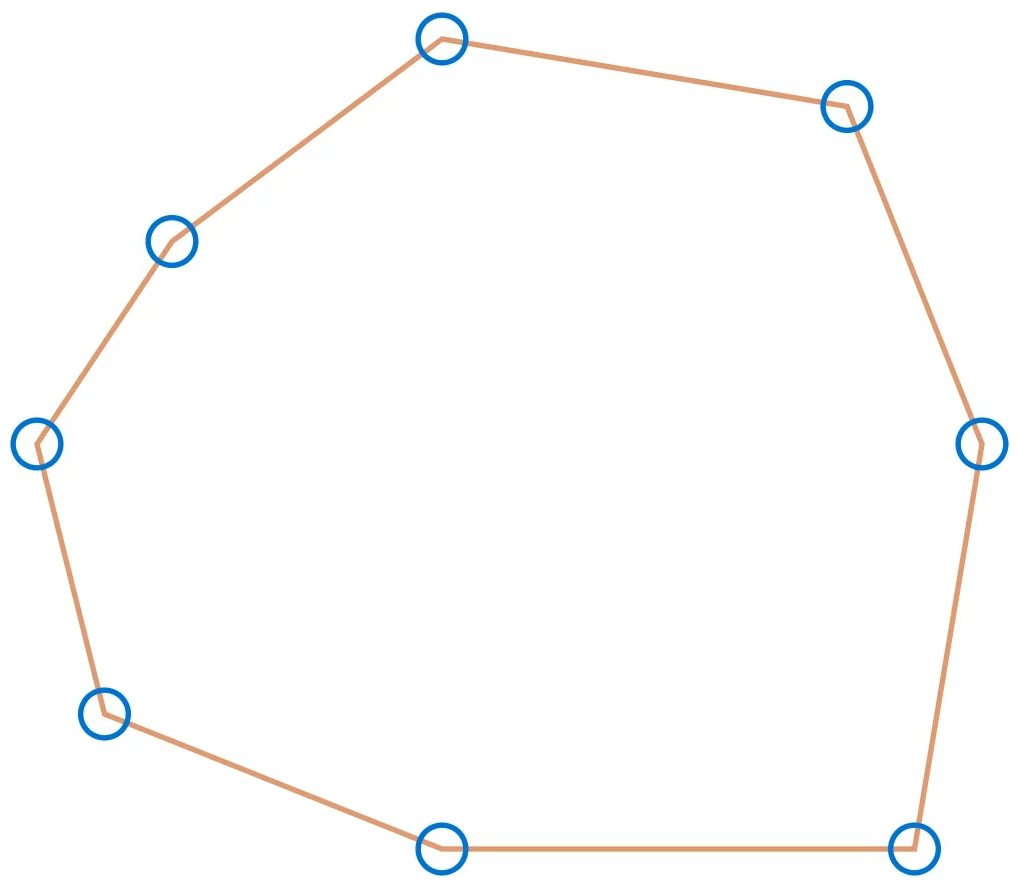
Fentebb láttuk, hogy a csúcsok helyzetének létezik határértéke. A határérték definíciójából adódóan ez azt jelenti, hogy az eredeti sokszög csúcsai tetszőlegesen közel juthatnak a határcsúcsukhoz, még ha nem is biztos, hogy elérik azt. Ezek alapján a csúcsok véges sok lépésben belépnek a határsokszög konvexitási tolerancia tartományába, tehát a sokszög véges sok lépésben konvex lesz.

A videó elkészítéséhez az első lépés a forgatókönyv megírása volt. Egy olyan kisfilmet szerettünk volna létrehozni, ami minél szélesebb körben érthető, befogadható és játékosabb hangulatú. Felmerült az is, hogy egy történet keretei között vezessük be a tételt, de végül ezt az ötletet elvetettük, mert úgy gondoltuk, hogy enélkül is érdekessé tudjuk tenni a videót. A forgatókönyv írásában a legnagyobb kihívás az volt, hogy eldöntsük, milyen részletességgel tárgyaljuk a bizonyítást. További nehézséget okozott, hogy a tételről kevés bizonyítás található az interneten, és azok közül is sok hiányos. Szerencsére Kézér Ildikó tanárnőhöz és dr. Vajda István tanár úrhoz fordulhattunk időközben kérdéseinkkel, és segítségükkel sikerült egy helyes bizonyítást összeraknunk. Az elkészített kisfilmben sem említettünk meg minden részletet, hiszen fontos szempont volt az is, hogy a videó ne legyen túl hosszú.

Összességében, habár végül nem nyertünk semmit a pályázaton, nagyon sok számunkra kedves és érdekes pillanatot köszönhetünk a 2022-es SoME-nak. Hogy csak egy példát említsünk: egy lazább forgatókönyvírás közben sikerült elírnunk a „tell” szót „tekku”-ra. Azóta „TEKKU” belsős poénként létezik négyünk között. „TADIUS” hasonlóképpen a „radius” szó elírásából keletkezett. Azóta mindketten szerves részei az életünknek (előbbit például a Bolyai Matematika Csapatversenyen is csapatnévként választottuk). Így természetesen, ha idén nyáron is kiírják a pályázatot, szeretnénk indulni rajta, és minden kedves Olvasónak is azt ajánljuk, hogy készítsen ő is valamilyen matematikával kapcsolatos munkát, mert matekból sosem elég.

A cikket dr. Besenyei Ádám tanár úr (1982–2022) ösztönzésére írtuk, dicsérő szavaiért most is hálásak vagyunk. Ő volt az, aki az általunk készített videó megtekintése után felvetette, hogy írjuk meg a pályamunka történetét. Ezt az írást az ő emlékének is ajánljuk.

Gardev Dániel, Hartmann Botond, Kovács Dominik, Varga Sebestyén,

az Óbudai Árpád Gimnázium speciális matematika tagozatos tanulói