Hosszú szövegű feladatok az érettségin

Negyven-ötven évvel ezelőtt még rendszerint olyanok voltak a matematika tankönyvek és feladatgyűjtemények, hogy csak az egyes témakörök legvégén, az utolsó néhány leckében került sor szöveges feladatokra. A tanítás úgy épült fel, hogy szép, egymásra épülő rendszerben megtanították a matematikai fogalmakat, pontos definíciókat, tételeket és módszereket. Az alkalmazás és a szöveges feladatok csak a fejezet végén jöttek szóba, amikor már biztosan kezelték a diákok a témakörön belül a matematika eszköztárát. A legtöbben, akik megszerettük a matematikát, azért szerettük meg, mert rendkívül érdekesnek és szépnek láttuk a matematika világát. Nem az volt az elsődleges kérdés számunkra, hogy hol lehet mindezt alkalmazni.

Az utóbbi évtizedekben azonban a tanítás során előtérbe került az alkalmazás, és előtérbe kerültek a szöveges feladatok. Az érettségi vizsgán sokszor találkozunk hosszú szövegű matematika feladattal. A legtöbb matematikatanárnak nem ezek a feladatok a kedvencei. Mégis, mivel az érettségi vizsgának ez része lett, tanárként nem bújhatunk ki a kérdés elől, hogyan tudjuk segíteni a diákokat a hosszabb szövegű feladatok megoldásában.

Miért történt ez a változás, miért kaptak nagyobb hangsúlyt a szöveges feladatok? Az okok között szerepel az, hogy az iskola nemcsak tudást, hanem praktikus tudást is szeretne közvetíteni a diákok felé. A matematika nemcsak egy önmagában szép és érdekes gondolatkör, hanem egy olyan eszköztár, ami kifejezetten alkalmas a minket körülvevő világ leírására, kutatására. A matematikai struktúrák a világ számos jelenségét kiválóan modellezik.

„A matematika a mintázatok tudománya, s e mintázatokra mindenütt rábukkanunk, bármerre tekintünk is: a fizikai Univerzumban, az élővilágban vagy akár tulajdon elménkben.” (Keith Devlin: A láthatatlan megjelenítése)

Ez a megközelítés azt vonja maga után, hogy tanárként egyaránt fontos feladatom, hogy magát a mintázatot megismertessem a diákokkal, valamint az, hogy a mintázat felismerésének és alkalmazásának útjára rámutassak. Maga a mintázat matematikai objektumokkal dolgozik, matematikai fogalmakat alkot, tételeket bizonyít, rendszerbe helyezi az ismereteket, módszereket és eljárásokat dolgoz ki. A mintázat felismerése és alkalmazása pedig a modellalkotás és modellezés. Sok esetben ez a modellalkotás mutat rá egy-egy matematikai fogalom szerepére, a matematikai struktúra (mintázat) tulajdonságaira, és újabb kérdésfelvetésekre inspirál. Az, hogy a matematikát nemcsak elnagyolt szöveges feladathoz, hanem érdekes és árnyalt szituációhoz kötjük, sok tanuló számára inspiráló lehet a matematika tanulásában és tanulmányozásában.

A szöveges feladatok tanítása ugyanakkor nem könnyű. Vannak, akik olvasási, szövegértési nehézségekkel küzdenek, számukra riasztó lehet a szöveg hossza. A feladat megoldásához türelemre, fókuszálásra van szükség, sok diák számára ez sem egyszerű. Időigényes része ez a tanításnak, a számos elvárás és követelmény között nehéz rá időt szakítani.

E nehézségek tiszteletben tartása mellett arra keresünk most válaszokat, hogy mi segíthet a hosszabb szövegű feladatok tanításában. Milyen ötletek, módszerek tehetik eredményesebbé a tanári munka ezen területét?

Sokat segít, ha a szöveges feladat érdekes. (Erre mutatunk példát az 1. feladatban.) Az érdekes feladat rendszerint valós vagy ahhoz közeli helyzetet mutat be. Olyan szituációt ír le, amelyhez érzelmileg is lehet kapcsolódni. Kíváncsivá tesz, s ez a motivációt is erősíti. Ilyen feladat esetében arra is lehetőség nyílhat, hogy a valódi helyzetet is megmutassuk egy fényképpel vagy videóval.

Fontos megmutatni, hogy az, hogy egy feladatnak hosszú a szövege, nem öncélú. A hosszabb szöveg oka sokszor az, hogy a világban előforduló helyzetek komplexek, összetettek. A helyzet elemzéséhez és a megfelelő matematikai modell megalkotásához pontosan kell ismerni a fogalmakat, pontosan megfogalmazott kérdésekre van szükség. (Erre mutatunk példát a 2. feladatban.)

A szöveges feladat megértését nagyban segíti a szöveg tagoltsága. Megfigyelhető, hogy az érettségi feladatokban is igyekeznek a feladat szerzői egy-egy részkérdés beszúrásával rávezetni a diákot a szöveg értelmezésére. (Erre mutatunk példát a 3. feladatban.) A tagolás történhet alpontokkal, kérdésekkel, de ezen kívül táblázattal, szakábrával, képpel. Sokat könnyít, ha a szövegbe bele lehet írni, vagy alá lehet húzni azt, ami fontos. Hosszú szövegű feladat esetében érdemes előkészíteni a tanórát feladatlappal, kitölthető táblázattal stb. (Megjegyzés: az A sorozatú tankönyvekben – ahol a tankönyv raktári száma kódszámban TA-ra vagy AE-re végződik – több ilyen feladat szerepel, hozzá tartozó szakábrával, táblázattal.)

A hosszú szövegű feladat esetében az egyéni olvasásra elegendő időt kell adni. Szerencsés, ha nemcsak a 12. évfolyamon kerül elő ez a típusú feladat, hanem már 9. osztálytól találkoznak ezzel a tanulók. Van idő, el kell olvasni, végig kell gondolni, végig kell számolni. Érdemes azzal is készülni az ilyen típusú órára, hogy plusz feladatot tudjunk adni annak, aki jóval hamarabb végez.

Végezetül felsorolunk néhány tanácsot, amit érdemes megfogalmazni a diákok számára a hosszú szövegű feladatokhoz kapcsolódóan az érettségi vizsga előtt.

Tanácsok, javaslatok hosszú szövegű feladat esetére

1. Olvasd el egyben, esetleg olvass el egy-egy bekezdést egyben!

2. Olvasd lassan, figyelmesen! Ha lehet, húzd alá, ami szerinted fontos!

3. Azonosítsd be, milyen adatok vannak megadva!

4. Fogalmazd meg a kérdést másként! (rövidebben, a matematikai modellhez kapcsolódóan)

5. Rajzolhatsz ábrát vagy táblázatot, ami segíthet.

Amikor a hosszú szövegű feladat motiválóan hat

1. feladat: (rövid változat)

Készítsünk dobozdiagramot a következő adatsokaságról!

7,93 7,71 8,19 8,9 7,66 7,97 8,12 8,02 7,94 7,9 8,16 7,89 7,44 8,09 7,51 7,94

Megoldás:

Dobozdiagram készítéséhez nagyság szerint növekvő sorrendbe kell állítani az adatsokaság elemeit:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.	16.
7,44	7,51	7,66	7,71	7,89	7,90	7,93	7,94	7,94	7,97	8,02	8,09	8,12	8,16	8,19	8,9

Meg kell határozni az adatsokaság mediánját, majd azután az alsó és felső kvartilisét.

Mivel 16 adat van, a medián a két középső, azaz a 8. és 9. adat számtani közepe. Tehát: 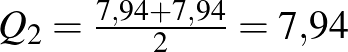$Q_{2}=\frac{7{,}94+7{,}94}{2}=7{,}94$ .

Az alsó kvartilis a medián előtti adatok, vagyis az első 8 adat mediánja. Ez tehát a 4. és az 5. adat számtani közepe: 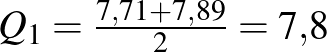$Q_{1}=\frac{7{,}71+7{,}89}{2}=7{,}8$ .

A felső kvartilis a medián utáni adatok, vagyis a második 8 adat mediánja. Ez tehát a 12. és a 13. adat számtani közepe: 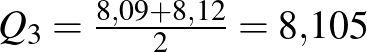$Q_{3}=\frac{8{,}09+8{,}12}{2}=8{,}105$ .

Ez a három adat határozza meg a doboz jellemzőit. A doboz szélességét a félterjedelem ( 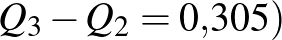$Q_{3}-Q_{2}=0{,}305)$ adja. Ha nincs kiugró adat, akkor a dobozhoz kapcsolódó „bajusz” szélső határa az adatsokaság minimuma illetve maximuma. Most az adatsokaság minimuma nem kiugró adat (az alsó kvartilistől való eltérése kisebb, mint a félterjedelem másfélszerese), de az adatsokaság maximuma egy kiugró adat, mert a felső kvartilistől való eltérése nagyobb, mint a félterjedelem másfélszerese ( 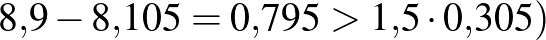$8{,}9-8{,}105=0{,}795>1{,}5\cdot 0{,}305)$ . A kiugró adatot külön ponttal jelöljük, és a „bajusz” szélét a legnagyobb olyan adat határozza meg, amelynek a felső kvartilistől való eltérése kisebb, mint a félterjedelem másfélszerese, tehát a jobb oldali „bajusz” felső széléhez tartozó adat 8,19.

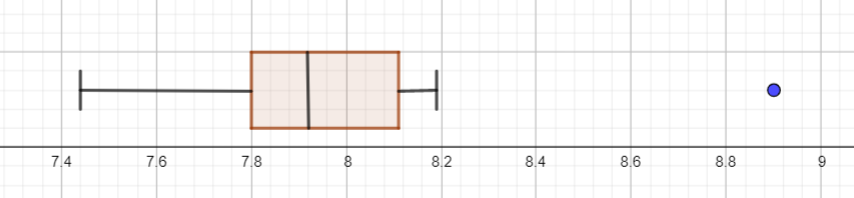
Ez a feladat ebben a formában egy eljárást gyakoroltat. Önálló gondolat nem kell hozzá, hanem a fogalmak pontos ismerete és alapos odafigyelés. Úgy is fogalmazhatunk, hogy egy „technikai” feladat.

A feladat érdekességét az adja, hogy egy valós adatsorhoz és egy rendkívül érdekes eseményhez és helyzethez kapcsolódik. 1968-ban Mexikóvárosban a férfi távolugrás döntőjében egészen fantasztikus világcsúcs született. Bob Beamon több, mint 70 cm-rel ugrott nagyobbat, mint mindenki más. 55 cm-rel döntötte meg a korábbi világcsúcsot. A feladatban szereplő számok az 1968-as olimpián a férfi távolugrásban született eredmények, méterben mérve.

Szöveges feladatként nemcsak arra mutat rá, hogy mit szemléltethet a statisztikában egy dobozdiagram, hanem sok diákot elgondolkodtat, beszélgetésre indít és motiváló erővel bír. A kiugró adatot jelző pont már nemcsak egy olyan apróság lesz, amire oda kell figyelni, hanem a minket körülvevő világ érdekességére mutat rá. Az új 12. osztályos tankönyvben a következő szöveggel jelenik meg ez a feladat:

Az atlétikai sportágak közül a férfi távolugrás világcsúcsának van a leghihetetlenebb története. Az 1968-as olimpián Mexikóvárosban Bob Beamon több, mint 70 cm-rel(!) ugrott távolabbra, mint mindenki más. 8,90 m-es ugrásával 55 cm-rel döntötte meg a korábbi világcsúcsot. Fantasztikus világcsúcsa szinte megdönthetetlennek tűnt. Azóta, megengedett hátszél mellett egyetlen versenyen tudtak ennél nagyobbat ugrani, 1991-ben. A világcsúcs azóta 8,95 m. (2022-ben 8,36 m volt a győztes eredmény az atlétikai világbajnokságon.)

helyezés	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.	16.
eredmény (m)	8,9	8,19	8,16	8,12	8,09	8,02	7,97	7,94	7,94	7,93	7,90	7,89	7,71	7,66	7,51	7,44

Ábrázold dobozdiagramon az 1968-as olimpia férfi távolugrás döntőjében született eredményeket!

Megjegyzések:

– A feladathoz kapcsolódóan érdemes a tanórán bemutatni Beaman híres ugrásának videófelvételét: https://www.youtube.com/watch?v=d9cqlo6Y1Zk.

– A férfi távolugrás világcsúcsának alakulásáról más érdekességek is olvashatók, találhatók, akár szakkönyvekben, akár az interneten.

A levegőben repülő Bob Beamon 1968-ban. Forrás: Wikipedia.

– Hasonló dobozdiagram készíthető Milák Kristóf 2022-ben 200 méteres pillangóúszásban elért világcsúcsáról. A 2022-es budapesti világbajnokságon Milák Kristóf eredményei kiugró adatként jelennek meg mind az elődöntőn, mind a döntőn elért eredmények között.

Amikor a hosszú szöveget a modern világ bonyolultsága indokolja

2. feladat: (rövid változat)

B és C összesen 3400 forintot helyezett valamely vállalatba. B a tőke és egy évi kamat fejében visszakap összesen 2070 forintot. C a tőke és a 16 havi kamat fejében 1920 forintot. Hány forintot helyezett B a vállalatba?

Az írásbeli érettségi vizsgálat tételei az 1892–93. iskola év végén;
V. kerületi állami főreáliskola, eredeti szöveg. Forrás: KÖMAL 1893. december

Kiegészítések:

A mai pénzügyi környezetben több pontosításra is szorul a feladat szövege. Az első kérdés, ami felmerül az olvasóban, hogy vajon mit jelent az, hogy valaki egy „vállalatba helyezett” el pénzt. Ez valószínűsíthetően nem részvény, mert akkor osztalékot kapna utána a tulajdonos, nem pedig kamatot, és az osztalék nem fix hozamú szokott lenni, s általában évenként fizetik. Nem gondolnánk hitelre sem, mert azt legjellemzőbben hitelintézet ad a vállalkozásoknak. Mai közgazdasági kifejezéssel élve a kötvény felelne meg a feladatban szereplő helyzetnek.

Fontos részletek továbbá, hogy a feladat szövegéből nem derül ki, hogy egyszerű kamatozás vagy kamatos kamatozás szerint történik az elszámolás. Vajon azonos-e a két befektető esetében az éves kamatláb? Félreérthető, hogy 16 hónapos futamidő esetében mi történik az 1 év lejártakor.

Egy mai érettségi feladatsorban mindezeket pontosabban kellene megfogalmazni, hogy egyértelmű legyen a diákok számára. Ezért jóval hosszabb lenne a feladat szövege. Például a következő módon jelenhetne meg a fenti feladat:

Egy vállalkozás egy kisebb beruházást tervez, az ehhez szükséges tőke előteremtéséhez kötvényeket bocsát ki. A kötvényeket magánszemélyek is megvásárolhatják. Egy adott kötvény megvásárlásakor a magánszemély szerződést köt a vállalkozással: a vásárláskor befizeti a vállalkozásnak a kötvényen szereplő tőkét, majd a szerződésben meghatározott idő elteltével a vállalkozás, egy előre rögzített kamattal visszavásárolja a személytől a kötvényt. Így a kötvény vásárlás által a vállalkozás kellő tőkéhez juthat, a kötvény megvásárlói pedig kedvező befektetéshez juthatnak.

Barna és Csaba kötvényt vásárolnak egy vállalkozástól, összesen 340 000 forint értékben. Barna olyan kötvényt választ, amely szerint a szerződése értelmében a vállalkozás egy év múlva vásárolja tőle vissza a kötvényt, és ekkor kifizet neki a tőke és egy évi kamat fejében összesen 207 000 forintot. Csaba olyan kötvényt választ, amely szerint a szerződés értelmében a vállalkozás 16 hónap múlva vásárolja vissza tőle a kötvényt, és ekkor egy összegben fizet ki neki a tőke és a 16 havi kamat fejében 192 000 forintot. A két esetben az éves kamatláb megegyezik. Egyszerű kamatozás történik, a 16 hónapra járó kamatláb az éves kamatláb 1,25-szorosa. Barna hány forintért vásárolt kötvényt?

Megoldás:

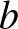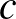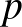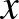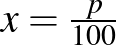Jelöljük a Barna által kötvénybe fektetett tőkét $b$ -vel, a Csaba által kötvénybe fektetett tőkét $c$ -vel! Legyen az éves kamatláb $p$ , jelöljük ennek századrészét $x$ -szel! ( $x=\frac{p}{100}$ )

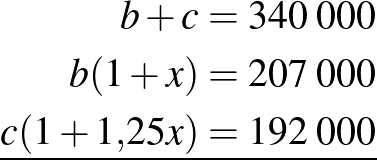
$\begin{equation*}\begin{aligned}b+c&=340\;000\\b(1+x)&=207\;000\\c(1+1{,}25x)&=192\;000\\\hline\end{aligned}\end{equation*}$

A második egyenletből fejezzük ki 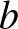$b$ -t, a harmadik egyenletből 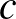$c$ -t és írjuk be az első egyenletbe!

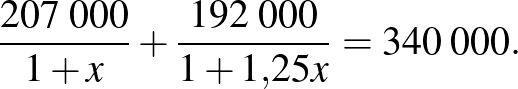
$\displaystyle \frac{207\;000}{1+x}+\frac{192\;000}{1+1{,}25x}=340\;000.$

Az egyenletet osszuk 1000-rel, majd szorozzuk 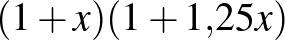-szel!

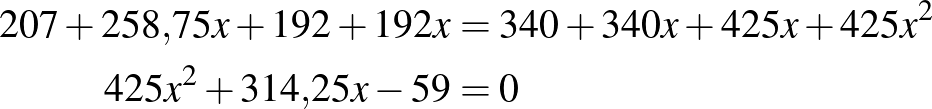
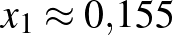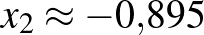Ennek megoldásai: $x_1\approx 0{,}155$ és $x_2\approx -0{,}895$ .

A negatív érték (a feladat szövegéből adódóan) nem megoldás. Az éves kamatláb tehát: 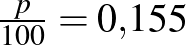$\frac{p}{100}=0{,}155$ vagyis $p=15{,}5$ (%).

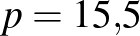A második egyenletből meghatározhatjuk a Barna által kötvénybe fektetett tőkét: 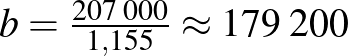$b=\frac{207\;000}{1{,}155}\approx 179\;200$ (forint).

Ellenőrzés:

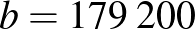$b=179\;200$ .

Ez kamatozik 15,5%-kal, így a járandóság egy év múlva 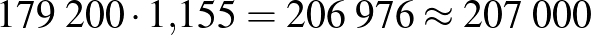$179\;200\cdot 1{,}155=206\;976\approx 207\;000$ (forint).

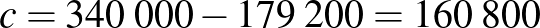$c=340\;000-179\;200=160\;800$ .

Az éves kamatláb 15,5, a 16 hónapra vonatkozó kamatláb 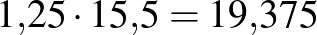$1{,}25\cdot 15{,}5=19{,}375$ (%).

A járandóság 16 hónap múlva 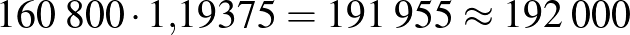$160\;800\cdot 1{,}19375=191\;955\approx 192\;000$ (forint)

Egy hosszú szövegű középszintű érettségi feladat

3. feladat: (2008. május, 18. feladat)

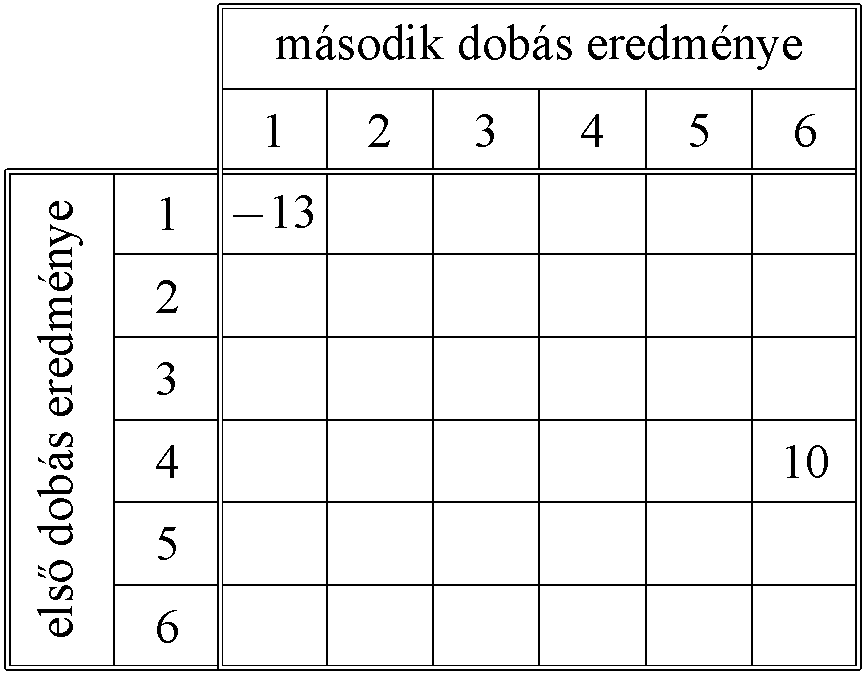
Egy szerencsejáték a következőképpen zajlik:

A játékos befizet 7 forintot, ezután a játékvezető feldob egy szabályos dobókockát. A dobás eredményének ismeretében a játékos abbahagyhatja a játékot; ez esetben annyi Ft-ot kap, amennyi a dobott szám volt.

Dönthet azonban úgy is, hogy nem kéri a dobott számnak megfelelő pénzt, hanem újabb 7 forintért még egy dobást kér. A játékvezető ekkor újra feldobja a kockát. A két dobás eredményének ismeretében annyi forintot fizet ki a játékosnak, amennyi az első és a második dobás eredményének szorzata. Ezzel a játék véget ér.

Zsófi úgy dönt, hogy ha 3-nál kisebb az első dobás eredménye, akkor abbahagyja, különben pedig folytatja a játékot.

a) Mennyi annak a valószínűsége, hogy Zsófi tovább játszik?

b) Zsófi játékának megkezdése előtt számítsuk ki, mekkora valószínűséggel fizet majd neki a játékvezető pontosan 12 forintot?

Barnabás úgy dönt, hogy mindenképpen két dobást kér majd. Áttekinti a két dobás utáni lehetséges egyenlegeket: a neki kifizetett és az általa befizetett pénz különbségét.

c) Írja be a táblázat üres mezőibe a két dobás utáni egyenlegeket!

d) Mekkora annak a valószínűsége, hogy Barnabás egy (két dobásból álló) játszmában nyer?

A feladat átlagosnál hosszabb szövegét az indokolja, hogy teljesen egyértelműen le kell írni a feladatban szereplő helyzetet. Fontos a lépések sorrendje. Ki mikor fizet, mikor dob, mikor kell döntést hoznia. A megoldást az segíti, hogy ezeket a lépéseket külön választjuk.

Első lépés: Zsófi befizet 7 forintot.

Második lépés: A játékvezető dob a kockával.

Harmadik lépés: Zsófi döntést hoz, hogy játszik-e tovább. A feladat szövege ismerteti a döntést: ha a dobás 1 vagy 2, akkor nem játszik tovább, ha 3, 4, 5 vagy 6, akkor tovább játszik. Innen tehát kétféle helyzet állhat elő.

a) Az első kérdés erre a harmadik lépésre vonatkozik. Azt kell meghatározni, hogy mekkora valószínűséggel lesz 3, 4, 5 vagy 6 a dobás eredménye. Ennek valószínűsége 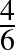$\frac{4}{6}$ , hiszen az összes lehetőség 6, ebből a kedvező lehetőségek száma 4 (és minden lehetőség egyformán valószínű).

b) A második kérdés arra az eseményre vonatkozik, amikor Zsófinak 12 forintot fizet ki a játékvezető. Figyeljük meg, hogy nem fogalmazhatunk úgy, hogy „Zsófi 12 forintot nyer”. Ez félreérthető lenne, hiszen kezdetben Zsófi 7 forintot befizetett, így tekinthetjük úgy, hogy a játék nyereménye 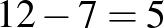$12-7=5$ forint, azonban tekinthetjük úgy is, hogy a nyeremény az, amit a játék végén visszakapunk. A mondat tehát valamivel hosszabb, mintha azt írnánk, hogy „Zsófi 12 forintot nyer”, de nincs benne az a bizonytalanság, hogy a 12 forint mire vonatkozik.

Fontos betoldás az is, hogy a kérdés arra vonatkozik, hogy a játék kezdetekor mennyi annak a valószínűsége, hogy a játékvezető 12 forintot fizet Zsófinak. A valószínűség vonatkozhatna egy másik pillanatra, helyzetre is, fontos az egyértelmű megfogalmazás.

A játékvezető ezekben az esetekben fizet ki 12 forintot:

első dobás	3	4	6
második dobás	4	3	2

A feladat érdekessége, hogy Zsófi döntése miatt nem állhat elő a két kockadobás után jól ismert 36 egyenlően valószínű elemi esemény. Ha az első dobás egyes vagy kettes, akkor nem történik második dobás.

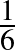$\frac{1}{6}$ valószínűséggel az első dobás egyes, ekkor nincs második dobás.

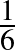$\frac{1}{6}$ valószínűséggel az első dobás kettes, ekkor nincs második dobás.

A többi esetben két dobás történik. Ez 24-féle lehetőség, és ez a 24 elemi esemény egymás között egyenlően valószínű. Elkészíthető tehát a következő táblázat, amely az egyes esetek valószínűségét tartalmazza:

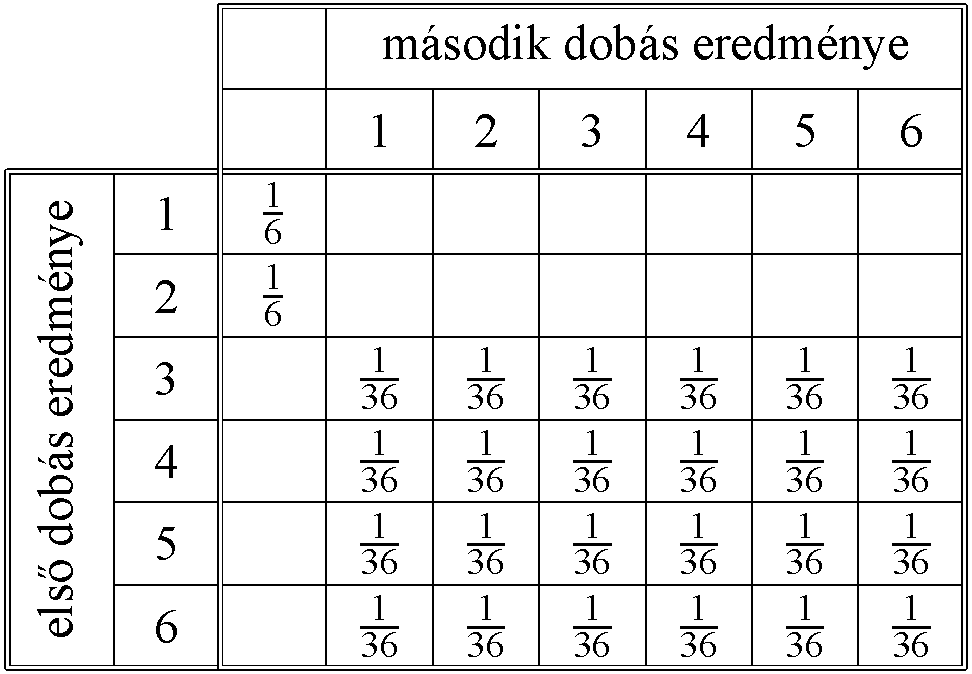
A játékvezető ennyit fizet Zsófinak az egyes esetekben:

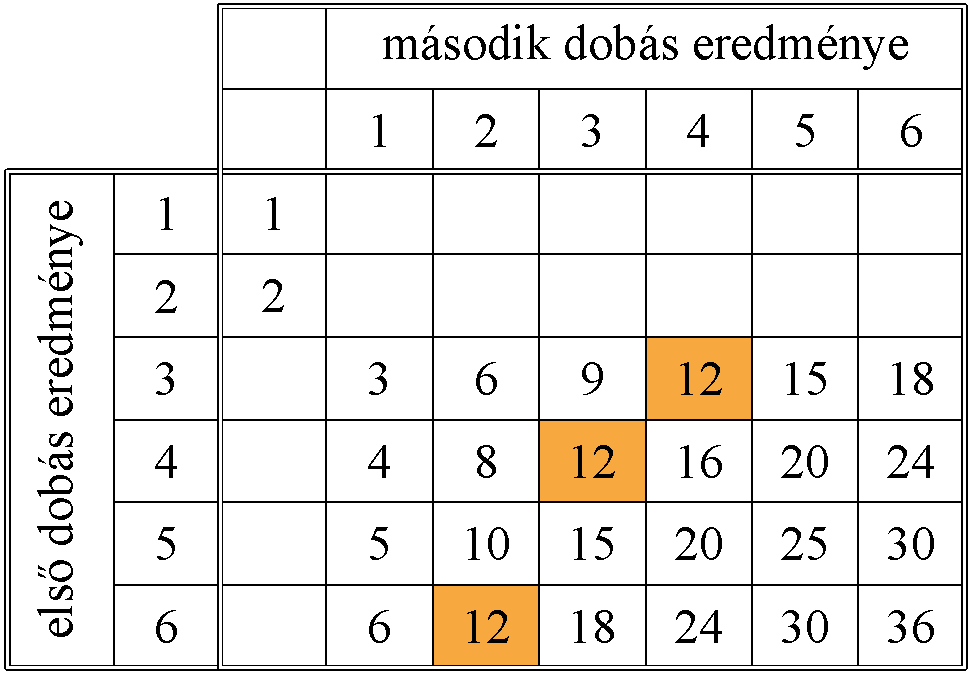
A színessel jelölt 3 eset valószínűsége 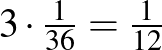$3\cdot\frac{1}{36}=\frac{1}{12}$ .

c) Barnabás esetében is ismerjük a 3. lépésben hozott döntését. Ő mindenképpen tovább játszik. Ekkor valójában Barnabás 14 forintot fizet be, 2 kockadobás történik, és a két dobás szorzata szabja meg, hogy mekkora összeget kap vissza. Barnabás egyenlege minden elemi esemény esetén: (a két dobás szorzata – 14).

A táblázat a konkrét eredményekkel nagyon sokat segít a feladat értelmezésében. Elkülöníti egymástól az elemi eseményeket és konkrét végeredményeket kapcsol hozzájuk. A táblázat kitöltése nagyban segíti majd a következő (d)) kérdés megválaszolását.

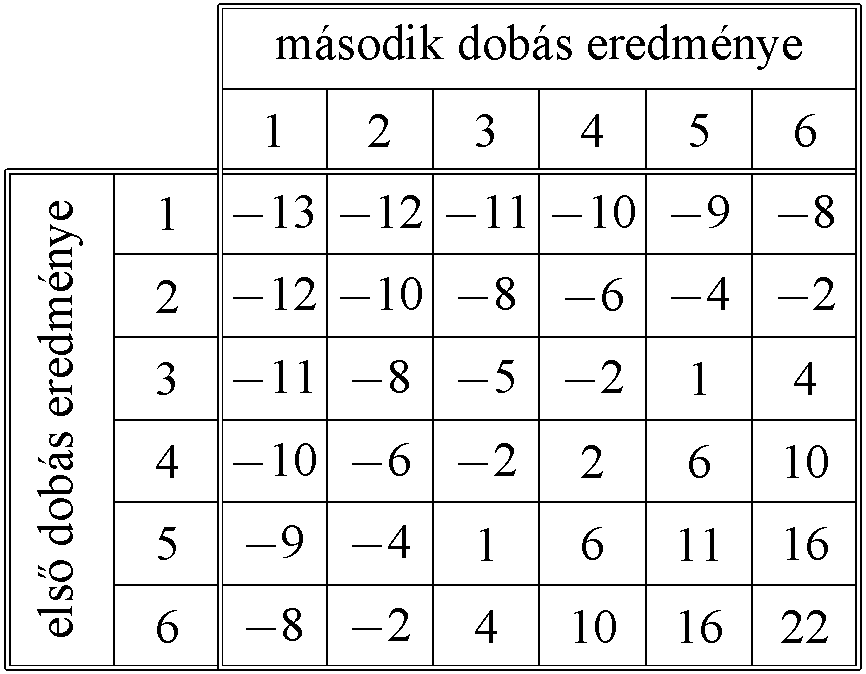
d) A táblázat a 36 elemi esemény esetében tartalmazza Barnabás egyenlegét. Barnabás nyereséges, ha az egyenleg pozitív. A pozitív eredményt tartalmazó cellák száma 13, ezért a helyes válasz 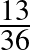$\frac{13}{36}$ .

Megjegyzés: A feladat megoldása után érdemes elbeszélgetni a kapott eredményekről. További kérdéseket fogalmazhatunk meg. Ilyen például, hogy mekkora a nyeremény várható értéke Barnabás és Zsófi esetében. Vajon miért dönt Zsófi úgy, hogy ha a dobás értéke kisebb, mint 3, akkor nem játszik tovább? Indokolt-e Zsófi döntése? Hogyan alakulna Barnabás esetében a várható érték, ha egy menetért nem 7, hanem 6 forintot kellene fizetnie?

Zsófi nyereményének várható értékéhez érdemes egy újabb táblázatot készíteni, amely azt tartalmazza, hogy mennyi Zsófi egyenlege az egyes esetekben:

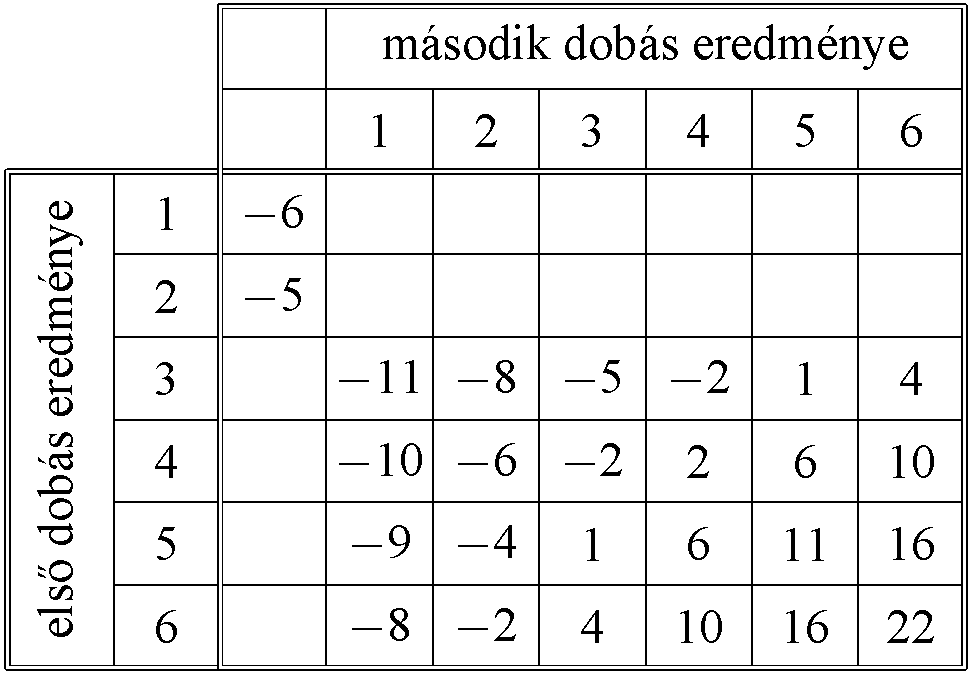
Megállapíthatjuk, hogy a valószínűségszámítás témakörében (is) nagyon pontosan és körültekintően kell fogalmazni. Emiatt lehet, hogy egy feladat szövege hosszú, de fontos az egyértelműség. Sokat segít a tagolás, és az, hogy lépésekre bontjuk a folyamatot. A táblázatok, szakábrák itt és más esetekben is nagyban segítik az adatok áttekintését.

Ebben a rövid cikkben igyekeztem ízelítőt adni abból, hogyan próbálom közelebb vinni a diákjaimat a hosszabb szövegű feladatok megoldásához, hogy felfedezhessék: a matematika szép, érdekes, és játékos.

Tamásné Kollár Magdolna
Pannonhalmi Bencés Gimnázium