A 2020-as NAT és az ehhez tartozó kerettanterv változásai miatt az érettségi követelmények megváltoztatása is szükséges volt. Jelen cikk szerzője részt vett abban a munkacsoportban, amelyik előkészítette a változtatási javaslatokat. Nyilvánvaló, hogy a középszintű érettségi követelmények nem tartalmazhatnak több kötelező ismeretet, mint a kerettanterv, viszont ami a kerettantervben benne van, azt érdemes az érettségi követelményekben is szerepeltetni. Ez tehát egy kétirányú mozgást indított el: egyfelől törölni kellett a középszintű követelmények közül azokat, amelyek nem szerepelnek a kerettantervben, másfelől a kerettantervbe bekerült újdonságokat, hangsúlyváltozásokat meg kellett jeleníteni az érettségi követelményekben. További kérdést jelentett az emelt szintű követelmények összeállítása, ugyanis ennek tartalmát semmilyen egyéb tantervi előírás nem szabályozza. A középszintről kikerülő követelmények esetében az új követelményeket összeállító csapat pontról pontra átgondolta, hogy az egyes ismeretek átkerüljenek-e az emelt szintű követelmények közé vagy kerüljenek ki onnan is. Általában úgy döntöttünk, hogy ezek kerüljenek át az emelt szintű követelmények közé. A tantervi változtatásoknak nem volt célja, hogy azoknak a diákoknak, akik eddig is jó teljesítményt nyújtottak matematikából, csökkenjenek a követelményeik. Tisztában voltunk azzal, hogy bizonyos iskolákban a közép- és emelt szintű követelmények közötti olló nagyobbra nyitása megnehezítheti az emelt szintű vizsgára való felkészülést, de bízunk abban, hogy ezt a NAT-ban biztosított óraszámkeretek között meg fogják tudni oldani a kollégák.
Ennek a cikksorozatnak az a célja, hogy segítse az érettségire felkészítő kollégák munkáját. Miután a középszintet érinti a nagyobb változás, ezért erre fogunk nagyobb hangsúlyt helyezni. Öt cikket olvashatnak az Érintő olvasói az elkövetkező bő egy évben, minden cikkben egy nagyobb témakörrel fogunk foglalkozni. A cikkekben először bemutatjuk az érettségi követelmények változását táblázatos formában. A táblázatban (piros színnel) jelezni fogjuk az újonnan megjelenő követelményeket és a törölt ismereteket is. (Ha egy követelmény átkerült középszintről emelt szintre, akkor azt csak a középszinten jelöljük kihúzással, hiszen eddig is része volt az emelt szintű követelményeknek.) A táblázat után a legfontosabb változásokat röviden megmagyarázzuk, értelmezzük, indokoljuk. Ezután néhány, középszinten is újdonságnak számító ismeret esetén mutatunk néhány olyan feladatot, amit a követelmények alapján el tudnánk képzelni egy feladatsorban. Hangsúlyozzuk, hogy ezek személyes elképzelések, az érettségi feladatokat összeállító bizottság nyilvánvalóan saját ötletei és szakmai meggyőződése szerint fog dolgozni.
1. Gondolkodási módszerek, halmazok, logika, kombinatorika, gráfok
E témakört (különösen a gondolkodási módszereket, a halmazokat és a matematikai logikát) elsősorban nem önállóan számonkérhető ismeretanyagként kell elképzelni, hanem olyan szemléletformáló, a matematikaoktatás egészét átszövő módszerek, illetve eszközök összességeként, amely szinte teljes egészében megjelenik minden további témakörben is.
|
TÉMÁK |
VIZSGASZINTEK |
|
|
Középszint |
Emelt szint |
|
|
1.1 Halmazok |
Ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát. |
|
|
1.1.1 Halmazműveletek |
Ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő műveleteket: unió, metszet, különbség. |
Ismerje és alkalmazza a de Morgan azonosságokat. |
|
1.1.2 Számosság, részhalmazok |
Tudja meghatározni véges halmazok elemeinek a számát. |
Ismerjen példát véges, megszámlálhatóan végtelen és nem megszámlálhatóan végtelen halmazra. |
|
1.2 Matematikai logika |
Tudjon egyszerű matematikai szövegeket értelmezni. |
|
|
1.2.1 Fogalmak, tételek és bizonyítások a matematikában |
Tudjon definíciókat, tételeket pontosan megfogalmazni, valamint egyszerű állításokat, tételeket bizonyítani. |
Ismerje az alábbi bizonyítási típusokat és tudjon példát mondani alkalmazásukra: direkt és indirekt bizonyítás, skatulyaelv, teljes indukció. Tudja megfogalmazni konkrét esetekben tételek megfordítását. |
|
1.3 Kombinatorika |
Tudjon egyszerű sorbarendezési, kiválasztási és egyéb kombinatorikai feladatokat megoldani. |
Ismerje, bizonyítsa és alkalmazza a permutációk (ismétlés nélkül és ismétléssel), variációk (ismétlés nélkül és ismétléssel), kombinációk (ismétlés nélkül) kiszámítására vonatkozó képleteket. |
|
1.4 Gráfok |
Tudjon konkrét szituációkat szemléltetni, és egyszerű feladatokat megoldani gráfok segítségével. Ismerje és alkalmazza gyakorlati feladatokban a gráf pontjainak fokszámösszege és éleinek száma közötti összefüggést. |
Definiálja és alkalmazza a következő fogalmakat: többszörös él, hurokél, séta, körséta, út, kör, összefüggő gráf, egyszerű gráf, teljes gráf, fa, komplementer gráf, izomorf gráfok. Bizonyítsa, hogy bármely (legalább kétpontú) egyszerű gráfban létezik két azonos fokszámú pont. |
Mint a fentiekből is kiolvasható, ebben a témakörben kevés változás található az érettségi vizsgakövetelményekben.
Középszinten a logikai szita alkalmazása két-három halmaz esetén – kimondatlanul – eddig is része volt a követelményeknek, ilyen feladatok gyakran szerepeltek az érettségi vizsgán. Ami itt a legnagyobb változásnak tűnik (egyszerű állítások, tételek bizonyítása), tulajdonképpen az sem igazi újdonság. Tisztázni kell egyfelől, hogy ez nem jelenti azt, hogy a középszintű matematika írásbeli vizsgán a diákoknak valamely, a követelményekben szereplő tétel bizonyítását kellene leírniuk. Ha valahol ezek a bizonyítások megjelenhetnek, az a szóbeli vizsga, erre a 2024-től érvényes vizsgaleírás is utal. (Itt emeljük ki újra, hogy – néhány ezzel kapcsolatos félreértés ellenére – matematikából középszinten 2024 után sem lesz mindenki számára kötelező szóbeli vizsgarész. Ez a lehetőség megmarad azoknak, akik az írásbelin 12 és 25% között teljesítettek, illetve azoknak, akik mentesülnek az írásbeli vizsgarész alól.)
A bizonyítások megjelenése a követelményekben azt jelenti, hogy ezentúl talán gyakrabban lehet majd olyan feladatokra számítani, amik úgy kezdődnek, hogy „Bizonyítsa be…”, „Mutassa meg…” vagy „Igazolja, hogy…”. Ilyen feladatok egyébként eddig is szerepeltek a középszintű feladatok között, íme:
2022. október, 18. feladat c) része:
Adott egy háromszög három csúcsa a koordinátasíkon: A(1; 2), B(5; 0) és C(6; 7). Igazolja, hogy az ABC háromszög egyenlő szárú!
2021. október, 18. feladat d) része:
Mutassa meg, hogy a 24! osztható 10 000-rel!
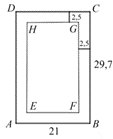2019. október, 16. feladat c) része:
Egy A4-es papírlap méretei: 21 cm × 29,7 cm. A szövegszerkesztő programok általában 2,5 cm-es margóval dolgoznak, vagyis a papírlap minden oldalától számítva egy-egy 2,5 cm-es sáv üresen marad (lásd az ábrát). A lap közepén a szövegnek fennmaradó rész szintén téglalap alakú. Zsófi szerint az ABCD és az EFGH téglalapok hasonlók. Igaza van-e Zsófinak? Válaszát indokolja!
Ami az emelt szintű követelmények változásait illeti: a szükséges és elégséges feltételek ismerete és alkalmazása eddig is része volt a (középszintű) követelményeknek; a gráfelméleti fogalmak közül az izomorf gráfok megjelenése jelent valódi újdonságot; az n pontú teljes gráf éleinek a száma akár középszintű követelmény is lehetne; az utolsó tétel pedig inkább az emelt szintű szóbeli vizsgarészen ad lehetőséget a vizsgázóknak arra, hogy egy gráfelméleti tétel húzása esetén ezt bizonyítsák be.
Lehetséges feladatok az egyes (megváltozott, új) követelmények esetén
Középszint
1. Tudja alkalmazni a logikai szita elvét két-három halmaz esetében.
1.1. Egy focicsapatnak 27 tagja van. A csapattagok közül 19-nek van tetoválása a karján, 14-nek van tetoválás a hátán, 9 játékosnak a karján és a hátán is van tetoválás.
a) Hány játékosnak van a karján, de nincs a hátán tetoválás?
b) Hány játékosnak nincs tetoválva sem a karja, sem a háta?
1.2. Egy országban két hírportálról lehet tájékozódni, a lakosság 70%-a olvassa valamelyiket. A hírolvasók 62%-a tájékozódik az egyikből, 43%-a olvassa a másikat. A lakosság hány százaléka olvassa mindkét sajtóterméket?
1.3. Egy művészeti iskola 35 tanulója jár rajzolni és 57 jár táncolni. Hányan vannak azok a tanulók, akik legalább az egyik foglalkozásra járnak,
a) ha a két foglalkozás különböző időpontokban van, és 12-en mindkettőre járnak?
b) ha a két foglalkozás egy időpontban van?
1.4. Az ELTE-n minden tanárszakos hallgató pontosan két szakon tanul. Egy tanárszakos összejövetelen 56 matek-, 18 kémia- és 42 angolszakos hallgató vesz részt. Közülük 10-en matek-kémia, 3-an kémia-angol és 15-en matematika-angol szakosok. Hányan vannak az összejövetelen?
1.5. Egy sportiskola egy évfolyamán 65-en fociznak, 45-en kosaraznak és 32-en úsznak. 20 diák focizik és kosarazik is, 25-en fociznak és úsznak, 15-en kosaraznak és úsznak. 8 olyan diák is van, aki mindhárom sportot műveli, az évfolyam 10 tanulója viszont egyik sportágban sem aktív. Hányan vannak az évfolyamon összesen?
1.6. Egy gimnáziumi évfolyam 45 tanulója közül 36 tanul angolul, 18 németül és 12 franciául. Mindenki legalább egyet tanul ezek közül, de 4 tanuló mindhárom nyelven képezi magát. Hány olyan tanuló van az évfolyamon, aki pontosan két nyelvet tanul ezek közül?
2. Tudjon definíciókat, tételeket pontosan megfogalmazni, valamint egyszerű állításokat, tételeket bizonyítani.
2.1. Egy háromszög egyik külső szöge a nem mellette fekvő belső szög kétszeresével egyenlő. Igazolja, hogy a háromszög egyenlőszárú!
2.2. Zsófi szerint, ha egy négyszögben két oldal párhuzamos, a másik kettő pedig egyenlő hosszú, akkor a négyszög paralelogramma. Igaza van-e Zsófinak? Válaszát indokolja!
2.3. Mutassa meg, hogy ha n pozitív egész szám, akkor n2 – 1 + (n – 1)2 páros!
2.4. Egy háromszög egyik oldalának a hossza kétszer akkora, mint a hozzá tartozó súlyvonal hossza. Mutassa meg, hogy a háromszög derékszögű!
3. Tudja megfogalmazni egy állítás megfordítását.
3.1. Adottak az alábbi állítások.
A = Ha egy háromszög két oldala egyenlő hosszú, akkor a háromszög szabályos.
B = Ha két szám egyenlő, akkor a két szám négyzete is egyenlő.
C = Ha egy szám kisebb, mint 5, akkor a négyzete kisebb, mint 25.
D = Ha a és b páros, akkor a + b páratlan.
E = Ha két szám előjele különböző, akkor a szorzatuk negatív.
a) Adja meg az állítások logikai értékét (igaz vagy hamis)! Válaszát indokolja!
b) Adja meg az állítások megfordítását! Adja meg a megfordítás logikai értékét! Válaszát indokolja!
4. Ismerje és alkalmazza gyakorlati feladatokban a gráf pontjainak fokszámösszege és éleinek száma közötti összefüggést.
4.1. Egy 7 fős tanulócsoportban szociometriai felmérést végeznek. Mindenki megjelöli, hogy kikkel van jó viszonyban a csoporton belül. Ha ketten egymást jelölik, akkor őket „barát”-nak tekinti a felmérés. A csoportvezető a felmérés után felírja, hogy kinek hány barátja van a csoporton belül. Az alábbiakban felsorolunk néhány számsorozatot. Melyek adhatják meg ezek közül a fenti felmérés eredményét? Válaszait indokolja!
a) 3, 3, 5, 7, 2, 4, 6
b) 1, 0, 3, 4, 6, 5, 3
c) 1, 3, 4, 5, 3, 5, 4
d) 1, 2, 3, 3, 3, 4, 6
e) Igazolja, hogy a valódi helyzetet leíró 7 szám között mindig van legalább kettő, ami egyenlő!
4.2. Egy gólyatáborba érkező 26 elsőéves hallgató között összesen 58 (kölcsönös) ismeretség van korábbról. Öt olyan hallgató van, aki 4 másikat, hat olyan hallgató van, aki 5 másikat, és hét olyan hallgató van, aki 6 másikat ismer. Tudjuk, hogy a többi hallgató mindegyikének ugyanannyi ismerőse van a táborban. Hány ismerőse van ezeknek a hallgatóknak a táborban?
Emelt szint
5. Definiálja és alkalmazza a következő fogalmakat: […] komplementer gráf, izomorf gráfok.
5.1. Állapítsa meg, hogy az alábbi gráfok izomorfok-e vagy sem! Válaszát indokolja!
a)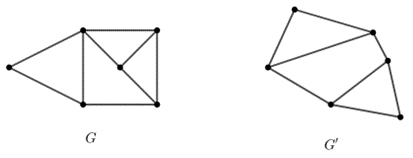 
b)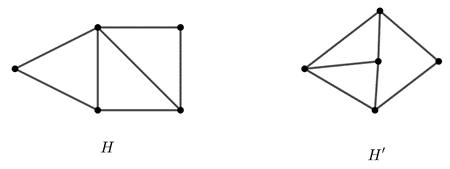 
c)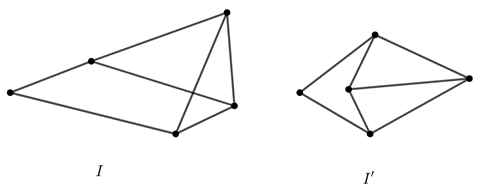 
5.2. Rajzoljon két 5-csúcsú, egyszerű gráfot, amelyekben a csúcsok fokszámai 1; 2; 2; 2; 3, de a két gráf nem izomorf!
5.3. Van-e olyan
a) 4 pontú,
b) 5 pontú,
c) 6 pontú,
egyszerű gráf, amely izomorf a komplementerével?
A feladatok megoldása hamarosan megjelenik az Érintő Facebook-oldalán.
Csapodi Csaba
ELTE TTK Matematikatanítási és Módszertani Központ
Rényi Alfréd Matematikai Kutatóintézet Módszertani Osztály
Megj. A cikk bevezető képének forrása: https://en.wikipedia.org/wiki/pl:User:Marcin_Otorowski.