Bevezető
A cikksorozat utolsó részében főként az egészségügyi tesztek megbízhatóságával kapcsolatos számolásokat végzünk. Az emelt szintű matematika érettségin ezek a problémák típusfeladatnak számítanak, általánosítás nélkül viszont az alacsonyabb évfolyamok számára is feldolgozható a téma kicsit komplexebb százalékszámítás-feladatként tálalva. Zárásként röviden megnézzük, hogy hogyan határozzák meg a vakcinák hatékonyságának százalékos értékét.1
Az egészségügyi tesztek megbízhatósága2
Tesztek specificitása és szenzitivitása
Az egészségügyi tesztek közül a bináris teszteket fogjuk vizsgálni. Binárisnak nevezzük a tesztet akkor, ha kétféle végeredményt adhat: az egyed rendelkezik vagy nem rendelkezik a vizsgált tulajdonsággal. Az eredményt az előbbi esetben pozitívnak, utóbbi esetben negatívnak nevezzük. A tesztek általában nem tökéletesek, két irányban is tévedhetnek: adhatnak hamis pozitív, illetve hamis negatív eredményt.
| a valós állapotnak megfelelő érték | ||
| a teszt eredménye | pozitív | negatív |
| pozitív | valós pozitív | hamis pozitív |
| negatív | hamis negatív | valós negatív |
 Hamis pozitív eredmény: ha valakinek, aki nem rendelkezik az adott tulajdonsággal, a teszt pozitív értéket ad.
Hamis pozitív eredmény: ha valakinek, aki nem rendelkezik az adott tulajdonsággal, a teszt pozitív értéket ad.
Egy teszt specificitása azt mutatja meg, hogy milyen arányban lehet vele a valódi negatívakat beazonosítani. Ezt a tulajdonságot rontják le a hamis pozitívak. A specificitás tehát egy feltételes valószínűség: feltéve, hogy az alany egészséges, mekkora valószínűséggel lesz a teszteredmény negatív.
Kiszámítási módja: 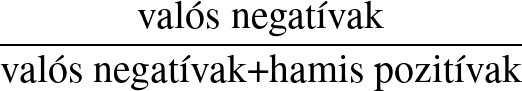 .
.
 Hamis negatív eredmény: ha valakiről, aki rendelkezik a beazonosítani kívánt tulajdonsággal a teszt negatív értéket ad.
Hamis negatív eredmény: ha valakiről, aki rendelkezik a beazonosítani kívánt tulajdonsággal a teszt negatív értéket ad.
Egy teszt szenzitivitása vagy érzékenysége azt mutatja meg, hogy milyen arányban lehet vele a valódi pozitívakat beazonosítani. Ezt a tulajdonságot rontják a hamis negatívak. A szenzitivitás szintén egy feltételes valószínűség: feltéve, hogy az alany beteg, mekkora valószínűséggel lesz a teszteredmény pozitív.
Kiszámítási módja: 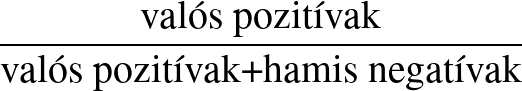 .
.
Ha ismerjük az érzékenységet és a specificitást, valamint tudjuk, hogy az adott tulajdonság mennyire gyakori a populációban (ennek a jelentőségéről hamarosan beszélünk), akkor ki tudjuk számolni, hogy mennyire valószínű, hogy egy pozitív teszteredmény valós problémát takar, illetve hogy egy negatív eredmény valóban azt jelenti, hogy az illető egészséges. El is érkeztünk két újabb fogalom definiálásához:
 A pozitív prediktív érték a pozitív tesztet adókon belül a valóban pozitívak aránya. Ismét feltételes valószínűséggel van dolgunk: feltéve, hogy pozitív a teszt, mekkora valószínűséggel beteg az alany.
A pozitív prediktív érték a pozitív tesztet adókon belül a valóban pozitívak aránya. Ismét feltételes valószínűséggel van dolgunk: feltéve, hogy pozitív a teszt, mekkora valószínűséggel beteg az alany.
Kiszámítási módja: 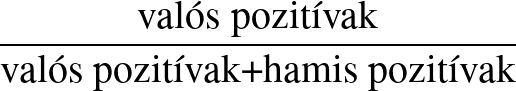 .
.
 A negatív prediktív érték a negatív tesztet adókon belül a valóban nem betegek aránya. Megint egy feltételes valószínűség: feltéve, hogy negatív a teszt, mekkora valószínűséggel egészséges az alany.
A negatív prediktív érték a negatív tesztet adókon belül a valóban nem betegek aránya. Megint egy feltételes valószínűség: feltéve, hogy negatív a teszt, mekkora valószínűséggel egészséges az alany.
Kiszámítási módja: 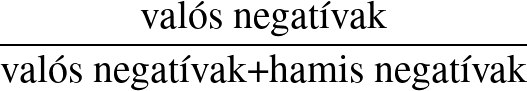 .
.
A tesztek specificitásáról és szenzitivitásáról a Zállatorvos Mire mész a teszttel? – Ellenanyagkimutatás című videójában szemléletes bemutatást láthatunk 6:24–8:07 között.
Gyorstesztek megbízhatósága
A diagnosztikai tesztek közül először a koronavírus ellenanyagtesztek tulajdonságait fogjuk megvizsgálni. (Az ellenagyagtesztek azt hivatottak megmutatni, hogy a fertőzés vagy a vakcina hatására termelődött-e ellenanyag a szervezetünkben.) Gyorstesztnek azt a fajta tesztet nevezzük, ami a mintavétel helyszínén kiértékelhető, nem kell hozzá laboratórium, emiatt olcsóbb, mint a laboratóriumi teszt.3
Ismét a Zállatorvos említett látott videójához fordulunk (9:09), és megnézzük, hogy mennyi a pozitív prediktív, illetve negatív prediktív értéke egy olyan tesztnek, amelynek szenzitivitása és specificitása egyaránt nagyon jól hangzó 99%. A válasz: attól függ, hogy a populációnak mekkora része fertőzött a teszt végzésekor. (Ezt az arányt nevezzük prevalenciának.)
Végezzünk el két számolást ennek az igazolására.
1. eset: a populáció létszáma 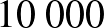 fő, a prevalencia
fő, a prevalencia 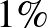 .
.
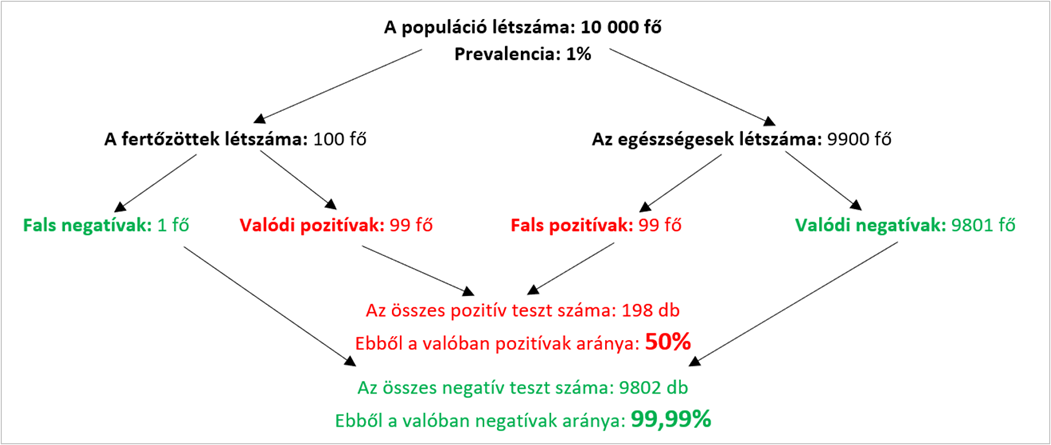
A számolást táblázat segítségével is elvégezhetjük:
| a valós állapot | összesen | ||
| a teszt eredménye | beteg | egészséges | |
| pozitív | 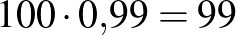 |
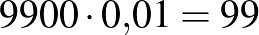 |
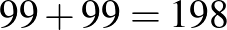 |
| negatív | 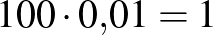 |
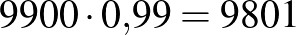 |
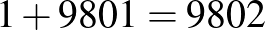 |
| összesen | 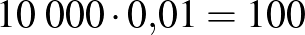 |
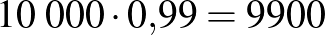 |
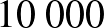 |
Pozitív prediktív érték: 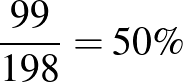 . Negatív prediktív érték:
. Negatív prediktív érték: 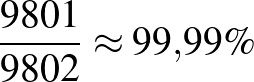 .
.
2. eset: a populáció létszáma 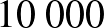 fő, a prevalencia
fő, a prevalencia 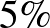 .
.
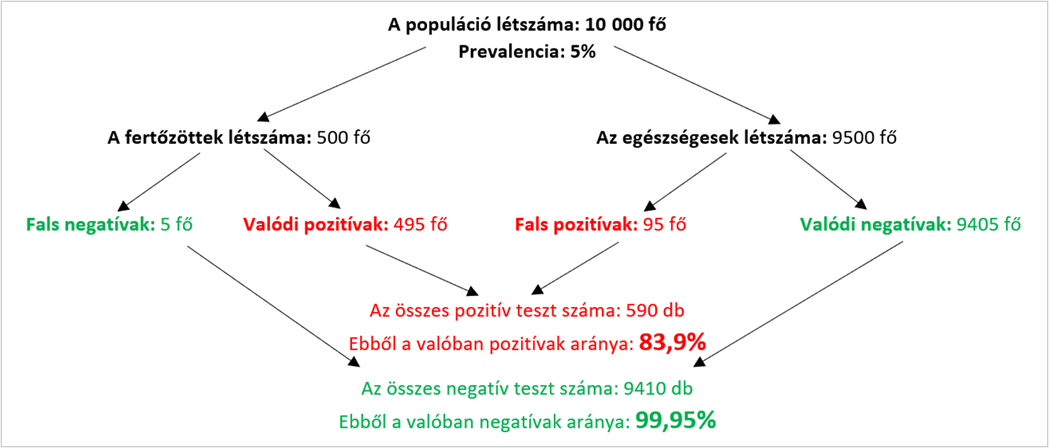
A számolás táblázattal:
| a valós állapot | összesen | ||
| a teszt eredménye | beteg | egészséges | |
| pozitív | 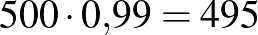 |
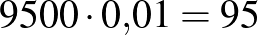 |
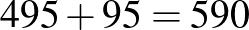 |
| negatív | 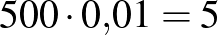 |
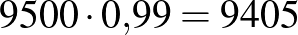 |
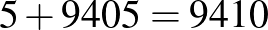 |
| összesen | 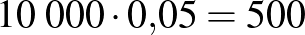 |
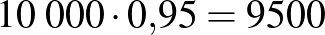 |
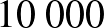 |
Pozitív prediktív érték: 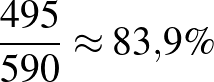 . Negatív prediktív érték:
. Negatív prediktív érték: 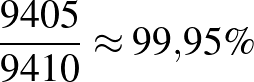 .
.
Vagyis a prevalencia növekedésével a teszt pozitív prediktív értéke nő, negatív prediktív értéke pedig csökken.
Ugyanezt a számolást a Semmelweis Egyetem 2020 májusi átfertőzöttségi tesztelése során kapott eredményekkel Magyarországra is kiszámíthatjuk, azaz megadhatjuk, hogy 2020 májusában körülbelül mennyi volt a 99%-os szenzitivitást és specificitást ígérő gyorstesztek pozitív prediktív, illetve negatív prediktív értéke. A SOTE reprezentatív tesztjei alapján az átfertőzöttség ebben az időpontban 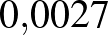 %–
%–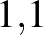 % közötti volt, számoljunk a köztes
% közötti volt, számoljunk a köztes 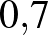 %-os értékkel!
%-os értékkel!
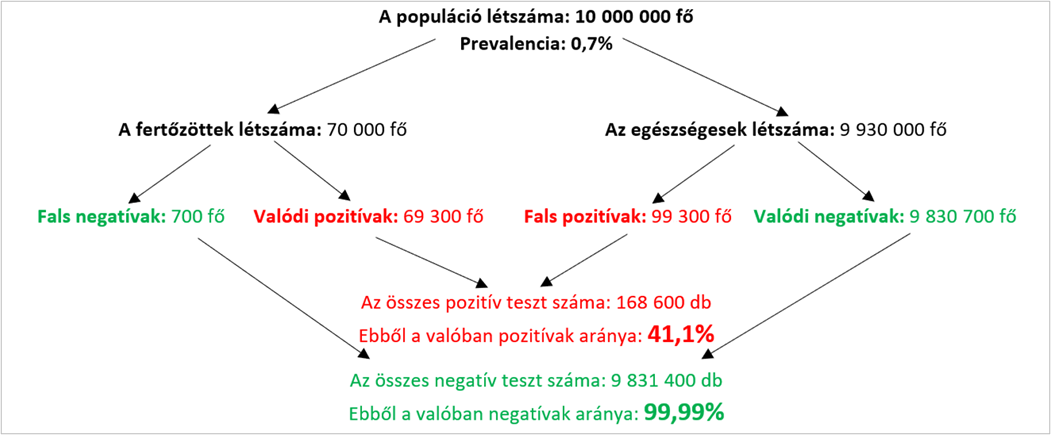
Táblázattal:
| a valós állapot | összesen | ||
| a teszt eredménye | beteg | egészséges | |
| pozitív | 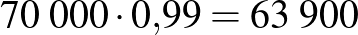 |
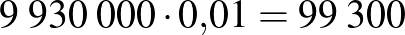 |
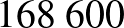 |
| negatív | 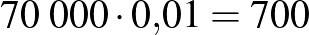 |
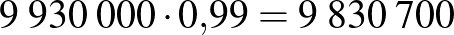 |
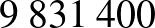 |
| összesen | 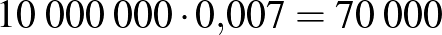 |
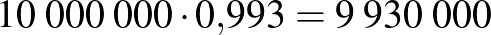 |
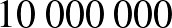 |
Pozitív prediktív érték: 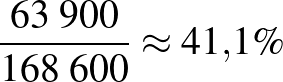 . Negatív prediktív érték:
. Negatív prediktív érték: 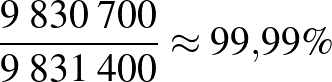 .
.
Hasonló számításokat más egészségügyi diagnosztikai vizsgálatokra is elvégezhetünk.
A Lyme-kór4 kimutatására használt teszt szenzitivitása 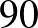 %, specificitása
%, specificitása 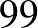 %. A Lyme-kór előfordulásának valószínűsége (a prevalencia) Magyarországon
%. A Lyme-kór előfordulásának valószínűsége (a prevalencia) Magyarországon 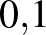 %. Adjuk meg a teszt pozitív prediktív, illetve negatív prediktív értékét, ha
%. Adjuk meg a teszt pozitív prediktív, illetve negatív prediktív értékét, ha 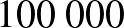 embert tesztelünk le! (A két érték valójában független attól, hogy hány embert tesztelünk. Erre később kitérünk.) A feladat abban tér el a korábbiaktól, hogy a szenzitivitás és a specificitás értéke különböző.
embert tesztelünk le! (A két érték valójában független attól, hogy hány embert tesztelünk. Erre később kitérünk.) A feladat abban tér el a korábbiaktól, hogy a szenzitivitás és a specificitás értéke különböző.

Táblázattal:
| a valós állapot | összesen | ||
| a teszt eredménye | beteg | egészséges | |
| pozitív | 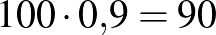 |
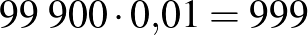 |
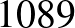 |
| negatív | 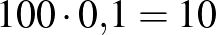 |
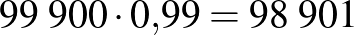 |
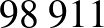 |
| összesen | 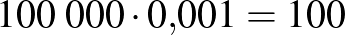 |
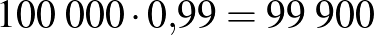 |
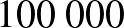 |
Pozitív prediktív érték: 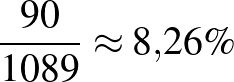 . Negatív prediktív érték:
. Negatív prediktív érték: 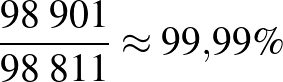 .
.
Az alábbi grafikon5 a prevalencia (a betegség fennállásának valószínűsége) függvényében mutatja a pozitív prediktív érték (zöld) és a negatív prediktív érték (piros) változását a fenti teszt esetében. A prevalencia növelésével a pozitív prediktív érték nő, a negatív prediktív érték csökken.
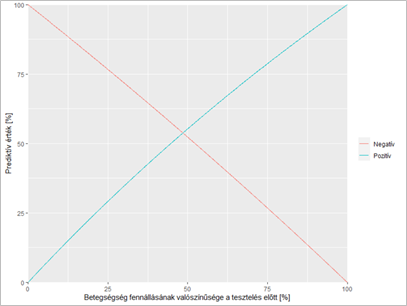
Lakos András és Ferenci Tamás cikkében a Lyme-kór tesztjénél látható alacsony pozitív prediktív értékkel kapcsolatos dilemmákról tájékozódhatunk alaposabban.
Az emlőrák szűrésére szolgáló mammográfiai vizsgálat esetén is a fenti számítási eljárás segít meghatározni, hogy egy pozitív lelet esetén mekkora a betegség valószínűsége. Az Egyesült Királyságban a nők körében az emlőrák prevalenciájára vonatkozó becslés 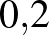 %, az 50 év feletti nők esetében
%, az 50 év feletti nők esetében 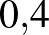 %6. A vizsgálat szenzitivitására és specificitására többféle becslés létezik, a mi esetünkben legyen a szenzitivitás 85%, a specificitás 90%7. Mekkora a mammográfiai vizsgálat pozitív prediktív, illetve negatív prediktív értéke, ha
%6. A vizsgálat szenzitivitására és specificitására többféle becslés létezik, a mi esetünkben legyen a szenzitivitás 85%, a specificitás 90%7. Mekkora a mammográfiai vizsgálat pozitív prediktív, illetve negatív prediktív értéke, ha 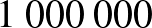 nőt vizsgálunk meg? A számítást végezzük el úgy is, ha csak 50 év feletti nőket szűrünk! A számolásunkat lerövidítheti, ha táblázatkezelő szoftvert használunk, és paraméterként felvesszük a prevalenciát, a szenzitivitást, a specificitást és a populáció méretét.
nőt vizsgálunk meg? A számítást végezzük el úgy is, ha csak 50 év feletti nőket szűrünk! A számolásunkat lerövidítheti, ha táblázatkezelő szoftvert használunk, és paraméterként felvesszük a prevalenciát, a szenzitivitást, a specificitást és a populáció méretét.
A mammográfiai szűrés értékelése az összes nő körében:
| a populáció mérete: | 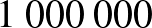 fő fő |
| prevalencia: | 0.20% |
| szenzitivitás: | 85.00% |
| specificitás: | 90.00% |
| a valós állapot | |||
| a teszt eredménye | beteg | egészséges | összesen |
| pozitív | 1700 fő | 99 800 fő | 101 500 fő |
| negatív | 300 fő | 898 200 fő | 898 500 fő |
| összesen | 2000 fő | 998 000 fő | 1 000 000 fő |
Pozitív prediktív érték: 1.67%. Negatív prediktív érték: 99.97%.
A mammográfiai szűrés értékelése az 50 év feletti nők körében:
| a populáció mérete: | 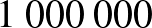 fő fő |
| prevalencia: | 0.40% |
| szenzitivitás: | 85.00% |
| specificitás: | 90.00% |
| a valós állapot | |||
| a teszt eredménye | beteg | egészséges | összesen |
| pozitív | 3400 fő | 99 600 fő | 103 000 fő |
| negatív | 600 fő | 896 400 fő | 897 000 fő |
| összesen | 4000 fő | 996 000 fő | 1 000 000 fő |
Pozitív prediktív érték: 3.30%. Negatív prediktív érték: 99.93%.
Azt látjuk, hogy a teszt pozitív prediktív értéke kicsi8. Ennek oka az alacsony prevalencia. A pozitív teszttel rendelkezők diagnózisát további komplex vizsgálatokkal lehet pontosítani.
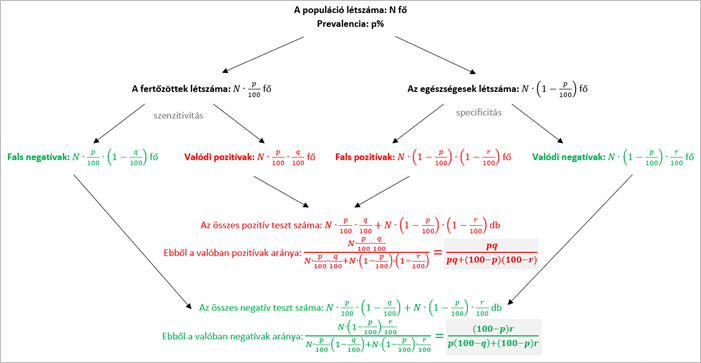
Általánosítás
Adjunk képletet a pozitív prediktív értékre és a negatív prediktív értékre a következő paramétereket használva:

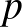 : prevalencia százalékban,
: prevalencia százalékban,

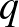 : szenzitivitás százalékban,
: szenzitivitás százalékban,

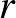 : specificitás százalékban,
: specificitás százalékban,

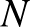 : populáció létszáma.
: populáció létszáma.
A feladattípus a Bayes-tétel segítségével is megoldható.
Tekintsük a következő eseményeket:
![]() : a vizsgált személy beteg.
: a vizsgált személy beteg.
 : a vizsgált személy egészséges.
: a vizsgált személy egészséges.
 : a vizsgált személy tesztje pozitív.
: a vizsgált személy tesztje pozitív.
 : a vizsgált személy tesztje negatív.
: a vizsgált személy tesztje negatív.
Az ismert valószínűségek:
prevalencia: 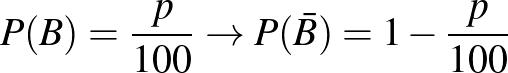 .
.
szenzitivitás: 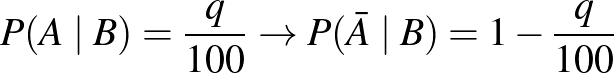 .
.
specificitás: 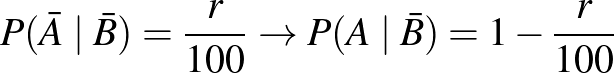 .
.
A kérdéses valószínűségek:
pozitív prediktív érték: 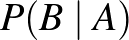 ,
,
negatív prediktív érték: 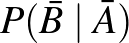 .
.
A pozitív prediktív érték meghatározása a Bayes-tétellel:
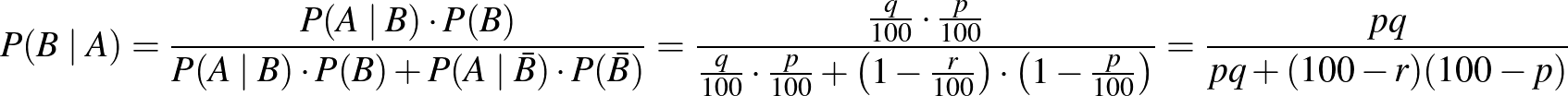 .
.
A negatív prediktív érték meghatározása a Bayes-tétellel:
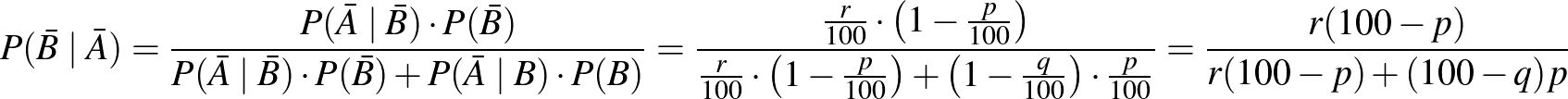 .
.
Egy ide vágó érettségi feladat
A 2017 májusi idegen nyelvű emelt matematika érettségi 8c feladata9 a gyorstesztek megbízhatóságáról szólt:
Járványos időszakban egy nagyváros lakóinak 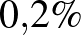 -a fertőzött a járványt okozó vírussal. Egy kereskedelmi forgalomban is kapható gyorsteszt azt ígéri a felhasználóknak, hogy a teszt kimutatja a vírusfertőzést. A termék leírásában ez áll: „A teszt a vírussal fertőzött embereknél
-a fertőzött a járványt okozó vírussal. Egy kereskedelmi forgalomban is kapható gyorsteszt azt ígéri a felhasználóknak, hogy a teszt kimutatja a vírusfertőzést. A termék leírásában ez áll: „A teszt a vírussal fertőzött embereknél 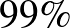 -os valószínűséggel mutatja ki a fertőzöttséget. A vírussal nem fertőzött emberek esetében olykor szintén fertőzöttséget jelez a teszt, ám ennek a téves jelzésnek a valószínűsége mindössze
-os valószínűséggel mutatja ki a fertőzöttséget. A vírussal nem fertőzött emberek esetében olykor szintén fertőzöttséget jelez a teszt, ám ennek a téves jelzésnek a valószínűsége mindössze 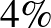 .' Tudjuk, hogy a város lakosságának
.' Tudjuk, hogy a város lakosságának 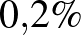 -a fertőzött a járványt okozó vírussal. Mutassa meg, hogy ha egy véletlenszerűen választott városlakó gyorstesztje fertőzöttséget mutat, akkor
-a fertőzött a járványt okozó vírussal. Mutassa meg, hogy ha egy véletlenszerűen választott városlakó gyorstesztje fertőzöttséget mutat, akkor 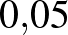 -nál kisebb annak a valószínűsége, hogy a tesztalany valóban vírusfertőzött (tehát a gyorsteszt nem a fertőzöttség megbízható kimutatására alkalmas)!
-nál kisebb annak a valószínűsége, hogy a tesztalany valóban vírusfertőzött (tehát a gyorsteszt nem a fertőzöttség megbízható kimutatására alkalmas)!
Ha a diákok levezették a feladattípus általánosítását, láthatták, ha nem vezették le, elárulhatjuk, hogy a végeredmény nem függ a populáció méretétől. Helyes eredményt kapunk tehát, ha a város lakóinak számára kiválasztunk egy konkrét értéket, és arra végigszámoljuk a feladatot.
A paraméterek:
 prevalencia:
prevalencia: 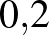 %,
%,
 specificitás:
specificitás: 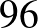 %,
%,
 szenzitivitás:
szenzitivitás: 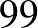 %,
%,
 a populáció létszáma legyen
a populáció létszáma legyen 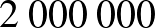 fő abban az esetben, ha a diákok még nem tudják általánosítani a feladatot.
fő abban az esetben, ha a diákok még nem tudják általánosítani a feladatot.
Megoldás, ha 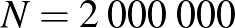 fő:
fő:
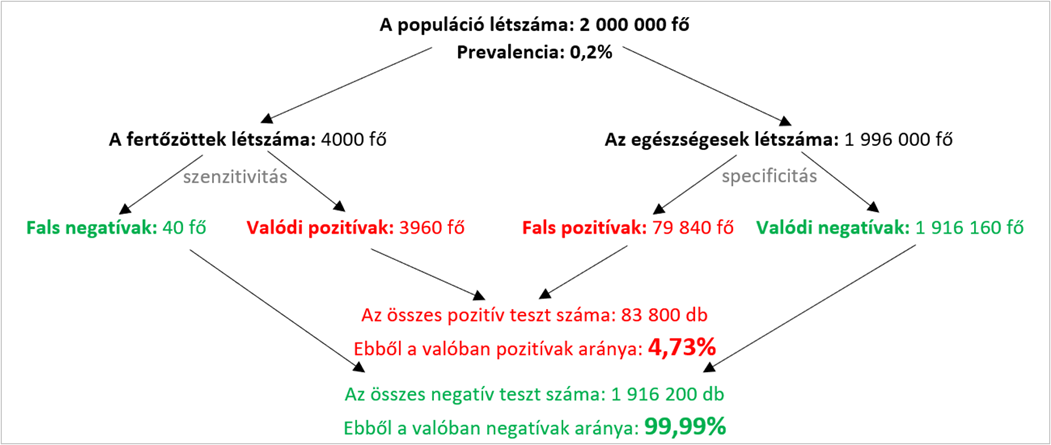
Táblázattal:
| a valós állapot | összesen | ||
| a teszt eredménye | beteg | egészséges | |
| pozitív | 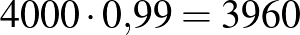 |
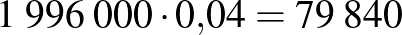 |
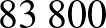 |
| negatív | 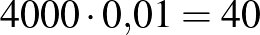 |
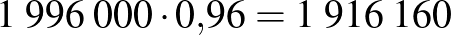 |
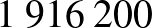 |
| összesen | |
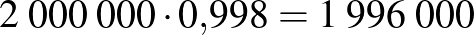 |
 |
Pozitív prediktív érték: 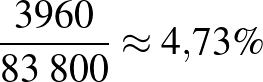 . Negatív prediktív érték:
. Negatív prediktív érték: 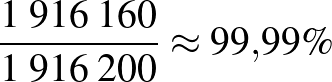 .
.
Megoldás általánosan a Bayes-tétellel:
Események:
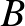 : a vizsgált személy beteg
: a vizsgált személy beteg
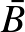 : a vizsgált személy egészséges
: a vizsgált személy egészséges
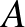 : a vizsgált személy tesztje pozitív
: a vizsgált személy tesztje pozitív
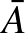 : a vizsgált személy tesztje negatív
: a vizsgált személy tesztje negatív
Az ismert valószínűségek:
prevalencia: 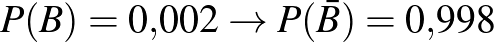 ,
,
szenzitivitás: 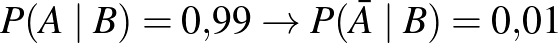 ,
,
specificitás:  .
.
A valószínűségek, amiket keresünk:
pozitív prediktív érték: 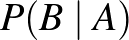 ,
,
negatív prediktív érték: 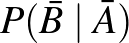 .
.
A pozitív prediktív érték meghatározása a Bayes-tétellel:
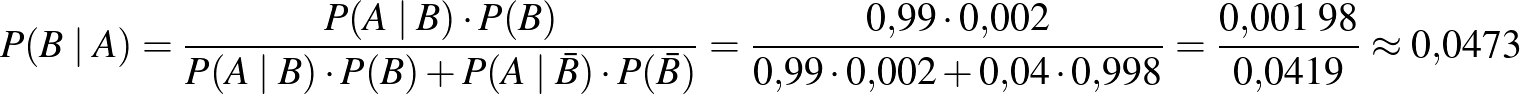 .
.
A negatív prediktív érték meghatározása a Bayes-tétellel:
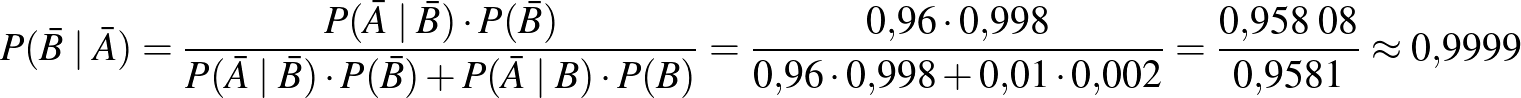 .
.
A feladattal részletesen foglalkozott Csapodi Csaba és Koncz Levente cikke. Továbbgondolták a problémát, és megfogalmazták a következő állítást: „Ha 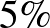 -ban betegek csak a pozitív teszteredményt produkálók, akkor hogy lehet megtalálni a ténylegesen betegeket? A pozitív eseteket érdemes egy második, vélhetően drágább, de ebben az irányban pontosabb eszközzel újratesztelni. De ha ilyenünk nincs, akkor a gyorsteszt másodszori alkalmazása is szóba jöhet: ha csak az első körben pozitív
-ban betegek csak a pozitív teszteredményt produkálók, akkor hogy lehet megtalálni a ténylegesen betegeket? A pozitív eseteket érdemes egy második, vélhetően drágább, de ebben az irányban pontosabb eszközzel újratesztelni. De ha ilyenünk nincs, akkor a gyorsteszt másodszori alkalmazása is szóba jöhet: ha csak az első körben pozitív 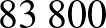 esetet teszteljük újra, akkor a második tesztelésen is pozitívnak bizonyulók már
esetet teszteljük újra, akkor a második tesztelésen is pozitívnak bizonyulók már 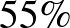 eséllyel tényleg fertőzöttek.”
eséllyel tényleg fertőzöttek.”
Igazoljuk, hogy a cikk állítása helyes!
A számolás az előzőhöz hasonló, de két paraméter változik. A bemenő létszám a pozitív tesztek száma (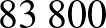 fő), a prevalencia pedig az első kör pozitív prediktív értéke, vagyis
fő), a prevalencia pedig az első kör pozitív prediktív értéke, vagyis 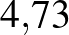 %. A teszt szenzitivitása és specificitása nem változik. Láttuk, hogy a tesztek mennyire érzékenyek a prevalenciára, ezért sejtjük, hogy az előzőnél jóval nagyobb százalékos arányt fogunk kapni a végén. (Ha konkrét létszámra, azaz
%. A teszt szenzitivitása és specificitása nem változik. Láttuk, hogy a tesztek mennyire érzékenyek a prevalenciára, ezért sejtjük, hogy az előzőnél jóval nagyobb százalékos arányt fogunk kapni a végén. (Ha konkrét létszámra, azaz 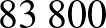 főre végezzük el a számolást, tört létszámokat, illetve darabszámokat kapunk, de ez a végeredményt nem befolyásolja.)
főre végezzük el a számolást, tört létszámokat, illetve darabszámokat kapunk, de ez a végeredményt nem befolyásolja.)

Táblázattal: adjunk általános megoldást, legyen a populáció létszáma 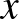 .
.
| a valós állapot | összesen | ||
| a teszt eredménye | beteg | egészséges | |
| pozitív | 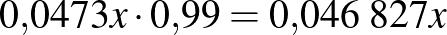 |
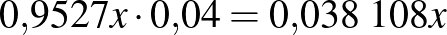 |
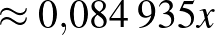 |
| negatív | 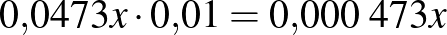 |
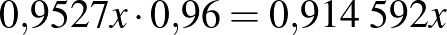 |
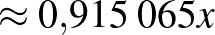 |
| összesen | 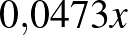 |
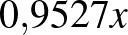 |
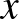 |
Pozitív prediktív érték: 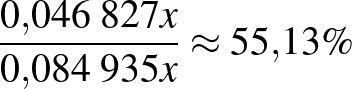 . Negatív prediktív érték:
. Negatív prediktív érték: 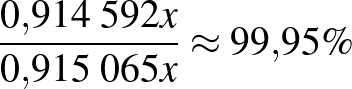 .
.
Megoldás Bayes-tétellel:
Események:
![]() : a vizsgált személy beteg.
: a vizsgált személy beteg.
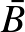 : a vizsgált személy egészséges.
: a vizsgált személy egészséges.
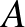 : a vizsgált személy tesztje pozitív.
: a vizsgált személy tesztje pozitív.
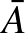 : a vizsgált személy tesztje negatív.
: a vizsgált személy tesztje negatív.
Az ismert valószínűségek:
prevalencia: 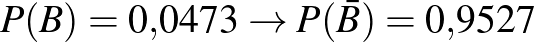 ,
,
szenzitivitás: 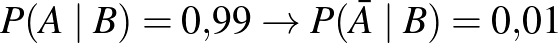 ,
,
specificitás:  .
.
A valószínűségek, amiket keresünk:
pozitív prediktív érték: 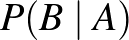 ,
,
negatív prediktív érték: 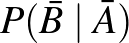 .
.
A pozitív prediktív érték meghatározása a Bayes-tétellel:
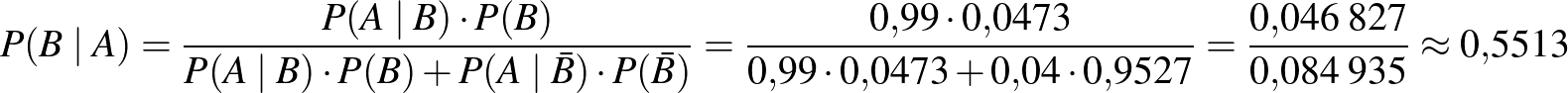 .
.
A negatív prediktív érték meghatározása a Bayes-tétellel:
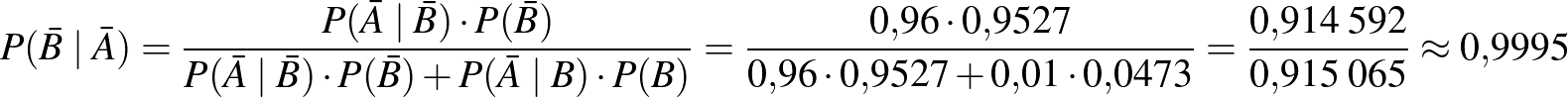 .
.
A koronavírus-tesztek megbízhatósága
A koronavírus esetén alkalmazott teszttípusok10 (PCR-, antitest-, antigén-teszt) hatékonyságával, különböző tesztek egymás után történő alkalmazásával kapcsolatos részletes számításokat találunk Dobreán István „A Bayes-statisztika alkalmazása mindennapi helyzetekben” című szakdolgozatában.
Hogyan számítják a vakcinák hatékonyságát?11
 Sok helyen hallottuk azt a kifejezést, hogy X vakcina ilyen és ilyen százalékos hatékonysággal véd a koronavírus ellen. Megnézzük, hogyan határozzák meg ezeket az értékeket. Előtte fontos kiemelni, hogy nem mindegy, hogy ez az adat megfertőződésre, tünetes megbetegedésre, súlyos betegség kialakulására, kórházba kerülésre avagy a halálos kimenetelre vonatkozik-e. (És akkor még nem beszéltünk a különböző koronavírus-variánsok elleni védelemről.)
Sok helyen hallottuk azt a kifejezést, hogy X vakcina ilyen és ilyen százalékos hatékonysággal véd a koronavírus ellen. Megnézzük, hogyan határozzák meg ezeket az értékeket. Előtte fontos kiemelni, hogy nem mindegy, hogy ez az adat megfertőződésre, tünetes megbetegedésre, súlyos betegség kialakulására, kórházba kerülésre avagy a halálos kimenetelre vonatkozik-e. (És akkor még nem beszéltünk a különböző koronavírus-variánsok elleni védelemről.)
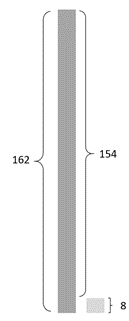
A Pfizer vakcinájának vizsgálatában körülbelül 43 000 ember vett részt (a pontos szám 43 661). Első körben feltételezzük, hogy a vizsgálatban résztvevőknek pontosan a fele kapott valódi vakcinát, a többieket hatóanyag nélküli placebóval oltották be12. Előbbit kísérleti csoportnak, utóbbit kontrollcsoportnak nevezzük. A vizsgált személyek közül a vizsgálati periódusban 170-en kapták el a Covidot, közülük 8-an kaptak hatóanyagot, 162-en placebót. A vakcina hatékonyságát az mutatja meg, hogy a kontrollcsoportban regisztrált megbetegedések számához képest milyen arányú a megelőzött megbetegedések száma a kísérleti csoportban.
A fenti esetben ez az arány 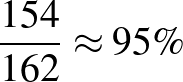 .
.
Ha a kontrollcsoport és a kísérleti csoport nem egyforma létszámú, akkor létszámok helyett százalékokkal végezzük el ugyanezt a számolást. A fenti adatokkal ez a levezetés így nézne ki:
A kísérleti csoportban a megbetegedések aránya 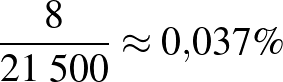 .
.
A kontrollcsoportban a megbetegedések aránya 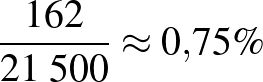 .
.
A megelőzött betegségek aránya a kísérleti csoportban: 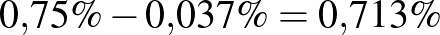 .
.
A megelőzött betegségek aránya a kontrollcsoport megbetegedéseihez képest: 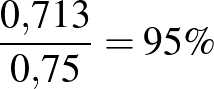 .
.
Fontos kiemelni, hogy a 95%-os hatékonyság nem azt jelenti, hogy 100 beoltott emberből 5 fog megbetegedni! A 95% az egyén, nem pedig a csoport szintjén hordoz jelentést: aki megkapja az oltást, annak 95%-kal kisebb esélye van arra, hogy megbetegedjen.
Nézzünk meg néhány fiktív forgatókönyvet.
Tegyük fel, hogy mindkét csoportban ugyanannyian betegedtek meg. Ekkor a vakcina hatékonysága 0%, hiszen a megelőzött megbetegedések aránya (azaz a törtünk számlálója) 0.
Az Egészségügyi Világszervezet (WHO) annak a vakcinának a sürgősségi jóváhagyását tartja elfogadhatónak, amelyik eléri legalább az 50 százalékos hatékonyságot. Ez szemléletesen azt jelenti, hogy a megelőzött megbetegedések aránya legalább 2-szer akkora, mint a kontrollcsoportban a megbetegedések aránya.
Tegyük fel, hogy a vizsgálat végén azt kapjuk, hogy a vakcina hatékonysága 70%, és tudjuk, hogy a kontrollcsoportban a megbetegedések aránya 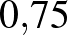 % volt. Számoljuk ki, hogy a kísérleti csoport hány százaléka kapta el a betegséget!
% volt. Számoljuk ki, hogy a kísérleti csoport hány százaléka kapta el a betegséget!
A kísérleti csoportban a megbetegedések aránya 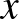 .
.
A kontrollcsoportban a megbetegedések aránya 0,0075.
A megelőzött betegségek aránya a kísérleti csoportban: 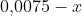 .
.
A megelőzött betegségek aránya a kísérleti csoport megbetegedéseihez képest: 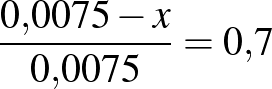 .
.
Az egyenlet megoldása: 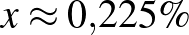 .
.
A különböző vakcinák hatékonysági mutatóit akkor lenne értelme összehasonlítani, ha azonos járványügyi helyzetben, azonos variánsra vizsgálnák őket. A Pfizernél jóval alacsonyabb százalékos mutatókkal rendelkező Janssen vakcinát például súlyosabb járványügyi helyzetben, fertőzőbb variánsok terjedése idején vizsgálták.
Függelék: a források ellenőrzésének fontosságáról
A felhasznált anyagok kapcsán érdemes kitérni a forrásaink ellenőrzésének fontosságára. A koronavírussal kapcsolatos információk esetén az sem mindegy, hogy az adott cikk vagy videó mikori, hiszen az új kutatási eredmények fényében változhat a tudásunk.
A linkelt forrásokból szemezgetve van, amikor a szerző szakértelme garantálja az információk hitelességét. Ferenci Tamás, Röst Gergely, Csoma Eszter és Constantin Tamás idézett cikkei, nyilatkozatai esetén ez a helyzet.
Sok esetben az írást megjelentető sajtóorgánum lehet a hitelesség biztosítéka, bár nem árthat a szerző személyének is utánajárni. Megbízhatunk a tudományos ismeretterjesztő folyóiratokban (pl. Természet Világa, Érintő), illetve a tudományt népszerűsítő weboldalakon megjelent cikkekben (Qubit, brilliant.org, Szkeptikus Társaság).
A különböző videómegosztó oldalakról származó anyagokat is érdemes ellenőrizni.
 A többször idézett Zállatorvos koronavírussal kapcsolatos videóit Kemenesi Gábor virológus lektorálta.
A többször idézett Zállatorvos koronavírussal kapcsolatos videóit Kemenesi Gábor virológus lektorálta.
 A Szertár csatorna a természettudományok népszerűsítését tűzte ki céljául.
A Szertár csatorna a természettudományok népszerűsítését tűzte ki céljául.
 A Zanza tv magyar nyelvű videós tananyagok gyűjteménye, melyeket tantárgy, évfolyam és témakör szerint csoportosítottak.
A Zanza tv magyar nyelvű videós tananyagok gyűjteménye, melyeket tantárgy, évfolyam és témakör szerint csoportosítottak.
 A Numberphile videóiban matematikusok szólalnak meg.
A Numberphile videóiban matematikusok szólalnak meg.
 A TED-Ed oktatási célra szánt rövid animációs filmek gyűjteménye.
A TED-Ed oktatási célra szánt rövid animációs filmek gyűjteménye.
 A 3Blue1Brown csatorna a matematikai összefüggések vizualizálását tűzte ki céljául.
A 3Blue1Brown csatorna a matematikai összefüggések vizualizálását tűzte ki céljául.
Volf Annamária
Városmajori Gimnázium
Lábjegyzetek
- 1 A tananyagban szereplő hivatkozások, görbék a 2021. júliusi állapotokat mutatják.
- 2 A témához fontos forrás Ferenci Tamás cikke: https://index.hu/velemeny/olvir/2020/05/02/agyorstesztekhasznalhatatlansagarol/
- 3 Forrás: Zállatorvos
- 4 Forrás: Lakos András, Ferenci Tamás https://index.hu/techtud/2019/06/28/tevhitek_nehezitik_a_lyme-kor_elleni_vedekezest/
- 5 https://index.hu/techtud/2019/06/28/tevhitek_nehezitik_a_lyme-kor_elleni_vedekezest/
- 6 Forrás: Kit Yates: Ne hidd el az igazságot – Miért (szinte) minden matematika? (Athenaum, 2020)
- 7 Forrás: http://daganatok.hu/rakszures/mellrak-szures/mammografia
- 8 Egy 2007-es kutatásban (https://pubmed.ncbi.nlm.nih.gov/26161749/) 160 nőgyógyászt kértek meg arra, hogy becsüljék meg, hogy ha egy páciens pozitív mammográfiai eredménnyel érkezik a rendelőjükbe, mekkora eséllyel van emlőrákja. A paramétereket a következők szerint adták meg: prevalencia 1%, szenzitivitás 90%, specificitás 91%. A részvevők többsége a megadott válaszlehetőségek közül (81%, 90%, 10%, 1%) a 81%-ot választotta. A helyes válasz a 10%.
- 9 Feladatsor: http://dload.oktatas.educatio.hu/erettsegi/feladatok_2017tavasz_emelt/e_matma_17maj_fl.pdf , pontozókulcs: http://dload.oktatas.educatio.hu/erettsegi/feladatok_2017tavasz_emelt/e_matma_17maj_ut.pdf
- 10 A koronavírus diagnosztizálására használt teszttípusokról Csoma Eszter mikrobiológus összefoglalójából tájékozódhatunk részletesebben: https://tudomany.hu/cikkek/a-koronavirus-fertozes-kimutatasanak-utvesztoi-azaz-melyik-teszt-modszer-mire-es-hogyan-hasznalhato-111225
- 11 Forrás: Constantin Tamás: Miért nincs még olyan, hogy „legjobb” COVID-19 oltás? https://mierted.com/miert-nincs-olyan-hogy-legjobb-covid-19-oltas/
- 12 Az orvosi kutatások módszertanának fontos fogalmait közérthetően magyarázza el a Szkeptikus Társaság cikke: https://szkeptikus.blog.hu/2008/01/01/nagy_adag_szkepticizmus_a_newsweek_szerk









