A 2021/2022. tanévi OKTV II. kategóriás döntőjének 2. feladata így szól:
Az 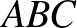 háromszögben
háromszögben 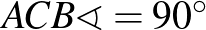 , a
, a  -hez tartozó magasság talppontja az
-hez tartozó magasság talppontja az 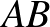 oldalon
oldalon 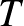 . Legyen az
. Legyen az 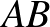 oldalt, a
oldalt, a 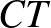 magasságot és az
magasságot és az 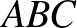 háromszög köré írt kör
háromszög köré írt kör  -t tartalmazó
-t tartalmazó 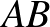 ívét belülről érintő két kör középpontja
ívét belülről érintő két kör középpontja  és
és 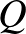 . Bizonyítsuk be, hogy
. Bizonyítsuk be, hogy 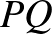 felezőpontja az
felezőpontja az 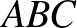 beírt körének középpontja.
beírt körének középpontja.
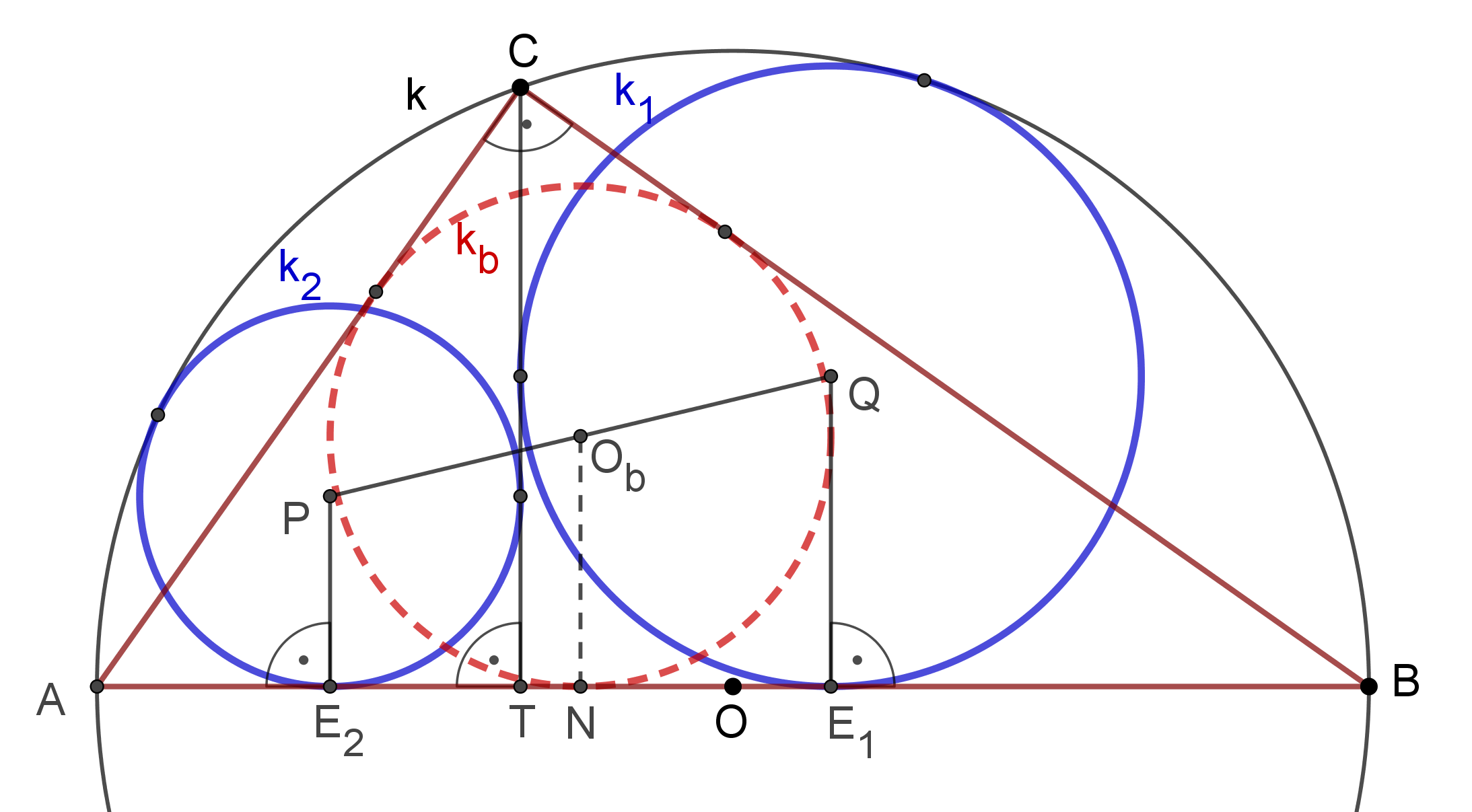
1. ábra
A versenybizottság által adott koordinátageometriai megoldás itt olvasható.
Az állítás meglepő és érdekes. Írásunkban három további megoldást mutatunk, rábízva az olvasóra a döntést, neki melyik tetszik legjobban.
1. Elemi geometriai megoldás:
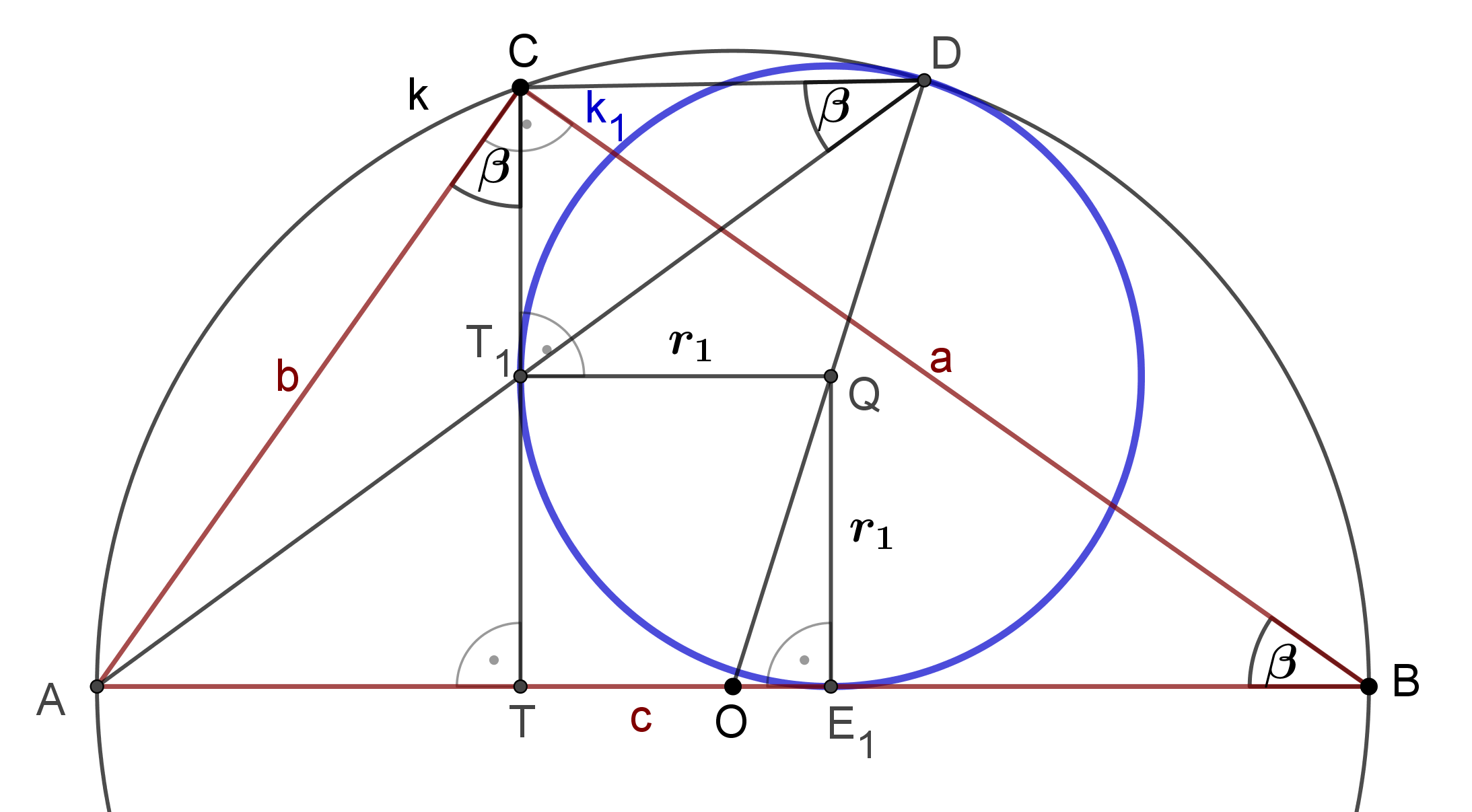
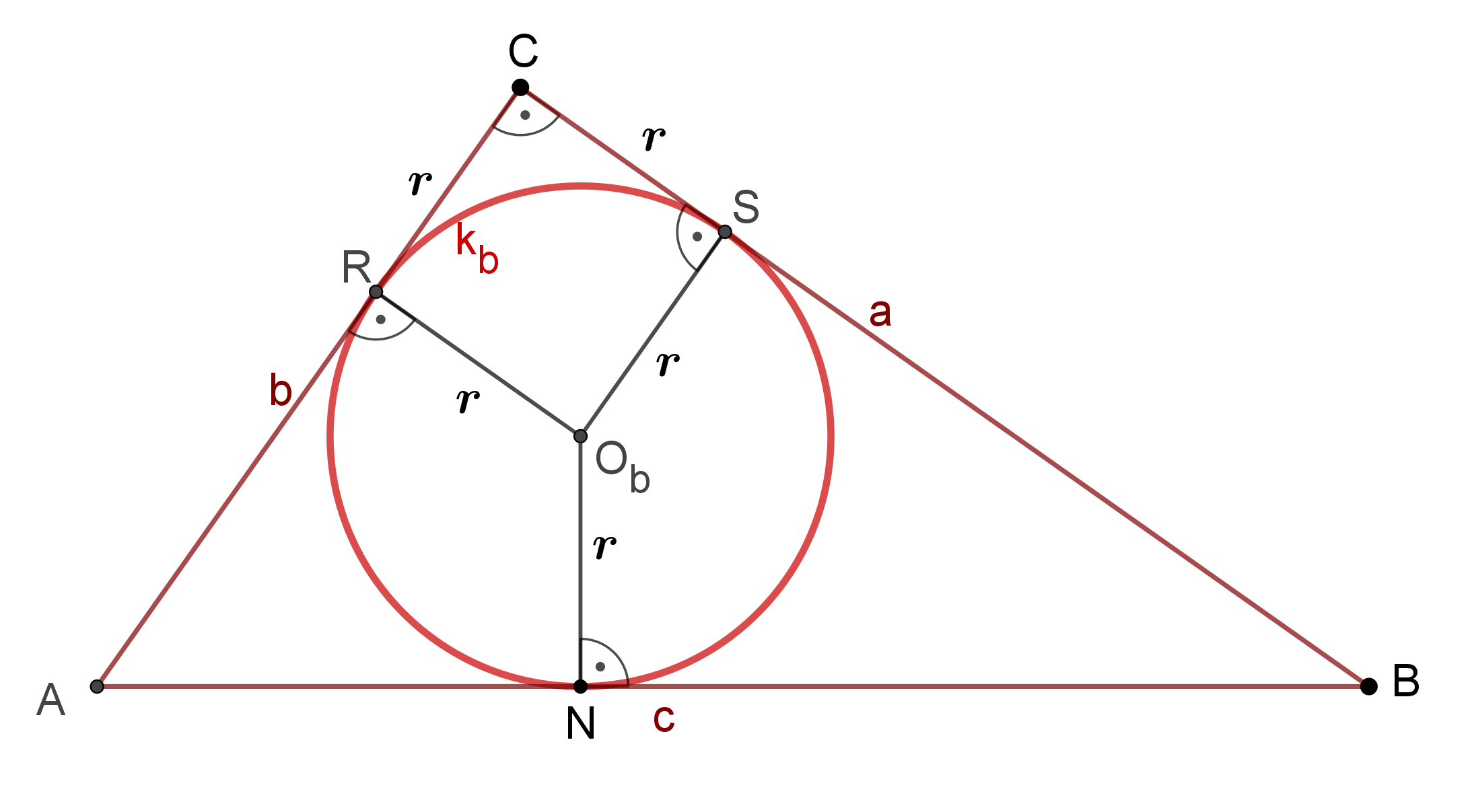
2. ábra
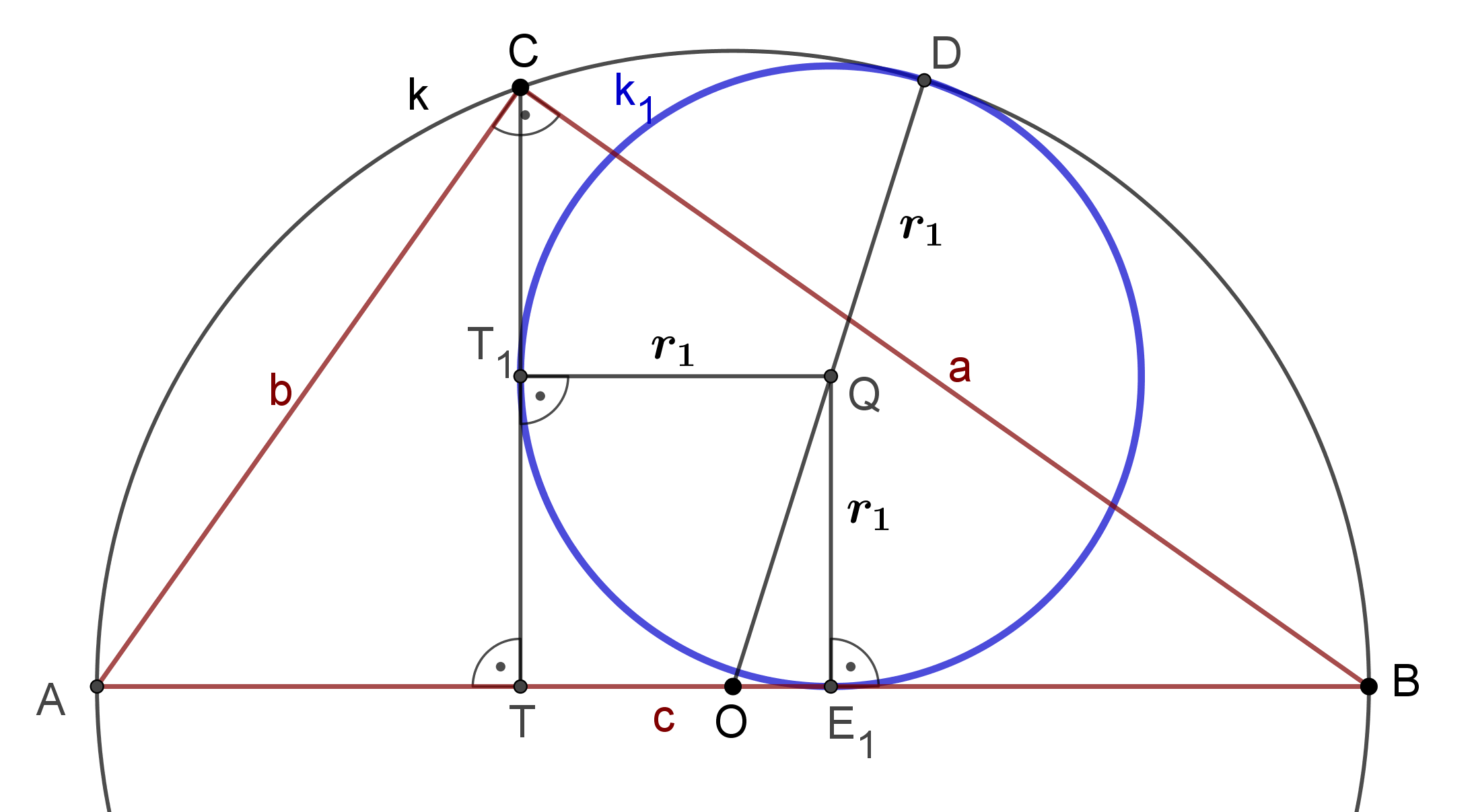
A 2. ábra jelöléseit használjuk. A 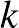 kör középpontja
kör középpontja  . Érintse a
. Érintse a 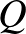 középpontú
középpontú 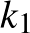 kör a
kör a 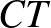 és
és  szakaszokat a
szakaszokat a 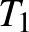 , illetve az
, illetve az 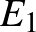 pontokban. Legyen
pontokban. Legyen 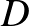 a
a 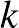 és
és 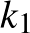 körök érintési pontja. A háromszög oldalait
körök érintési pontja. A háromszög oldalait 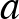 ,
, 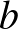 ,
, 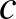 jelöli. Belátjuk, hogy
jelöli. Belátjuk, hogy 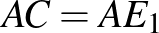 .
.
Elsőként tekintsük az 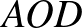 és
és 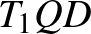 háromszögeket. Ezek egyenlő szárúak, hiszen száraik a
háromszögeket. Ezek egyenlő szárúak, hiszen száraik a 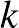 , illetve a
, illetve a 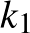 körök sugarai. A száraik párhuzamosak:
körök sugarai. A száraik párhuzamosak: 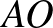 és
és 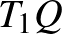 is merőleges
is merőleges 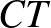 -re, továbbá
-re, továbbá  ,
, 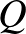 és
és 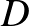 egy egyenesre esnek, mert a
egy egyenesre esnek, mert a 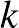 és
és 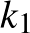 körök a
körök a 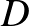 pontban érintik egymást. Ezért az alapjaik is párhuzamosak, azaz
pontban érintik egymást. Ezért az alapjaik is párhuzamosak, azaz 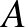 ,
, 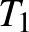 és
és 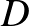 egy egyenesen vannak.
egy egyenesen vannak.
Jelölje 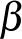 az
az 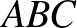 háromszög
háromszög 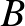 csúcsánál lévő szögét. Az
csúcsánál lévő szögét. Az 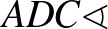 is
is 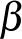 -val egyenlő, hiszen a
-val egyenlő, hiszen a 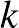 körben szintén az
körben szintén az 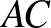 ívhez tartozó kerületi szög.
ívhez tartozó kerületi szög. 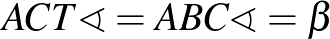 , mert merőleges szárú szögek. Az
, mert merőleges szárú szögek. Az  és
és  háromszögek
háromszögek 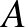 -nál lévő szöge közös, egy további szögük
-nál lévő szöge közös, egy további szögük 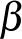 , ezért a két háromszög hasonló. A megfelelő oldalak aránya egyenlő:
, ezért a két háromszög hasonló. A megfelelő oldalak aránya egyenlő: 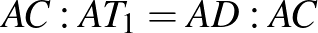 , átrendezve
, átrendezve 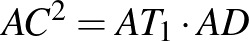 .
.
Az 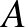 pont
pont  körre vonatkozó hatványa
körre vonatkozó hatványa 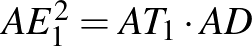 , tehát
, tehát 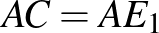 . Ez azt jelenti hogy a
. Ez azt jelenti hogy a 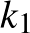 kör
kör  sugara
sugara 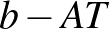 . Hasonlóan a
. Hasonlóan a  középpontú,
középpontú,  -t érintő
-t érintő 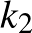 kör sugara
kör sugara 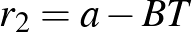 .
.
3. ábra
A 3. ábrán a beírt kör sugarát 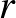 jelöli. Az
jelöli. Az 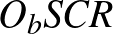 négyszög négyzet, ezért
négyszög négyzet, ezért 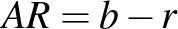 . Külső pontból a körhöz húzott érinőszakaszok egyenlőek, ezért
. Külső pontból a körhöz húzott érinőszakaszok egyenlőek, ezért 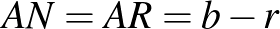 .
.
Hasonlóan 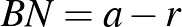 . Felhasználva, hogy
. Felhasználva, hogy 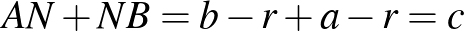 , a beírt kör sugarára teljesül, hogy
, a beírt kör sugarára teljesül, hogy 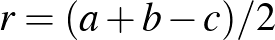 . Felhasználva az
. Felhasználva az  és
és  értékeket,
értékeket, 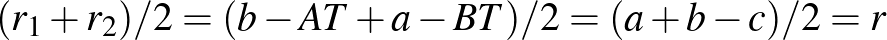 , hiszen
, hiszen  . Ezért az
. Ezért az  trapéz (1. ábra) középvonalának hossza
trapéz (1. ábra) középvonalának hossza 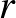 . A két érintési pont távolsága
. A két érintési pont távolsága 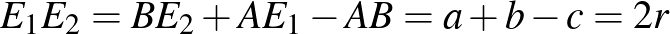 , továbbá
, továbbá 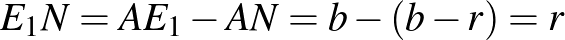 , tehát
, tehát 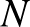 az
az 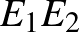 szakasz felezőpontja. Ezzel igazoltuk a feladat állítását,
szakasz felezőpontja. Ezzel igazoltuk a feladat állítását, 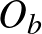 valóban a
valóban a 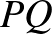 szakasz felezőpontja. Azt is látjuk, hogy a beírt kör érinti az
szakasz felezőpontja. Azt is látjuk, hogy a beírt kör érinti az 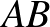 -re
-re 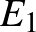 -ben és
-ben és  -ben állított merőlegeseket.
-ben állított merőlegeseket.
A megoldás alapvető lépése annak a belátása volt, hogy 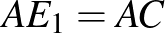 . Erre adunk további két bizonyítást.
. Erre adunk további két bizonyítást.
2. Használjuk ki két kör érintkezésének feltételét, számoljunk!
4. ábra
Thalész tétele miatt a 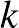 kör sugara
kör sugara  . Ha két kör érinti egymást, akkor a körök középpontjai és az érintési pont egy egyenesen vannak, így
. Ha két kör érinti egymást, akkor a körök középpontjai és az érintési pont egy egyenesen vannak, így 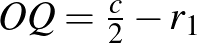 . Felhasználjuk, hogy az érintési pontba húzott sugár merőleges az érintőre, ezért az
. Felhasználjuk, hogy az érintési pontba húzott sugár merőleges az érintőre, ezért az 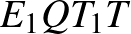 négyszög négyzet,
négyszög négyzet, 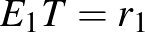 . Ezek alapján
. Ezek alapján 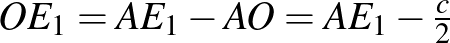 . Az
. Az 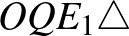 -ben alkalmazzuk a Pitagorasz-tételt:
-ben alkalmazzuk a Pitagorasz-tételt:
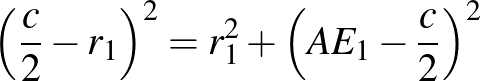
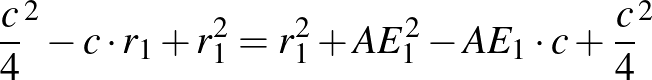
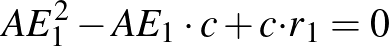 (*)
(*)Az  befogóra alkalmazzuk a befogótételt.
befogóra alkalmazzuk a befogótételt. 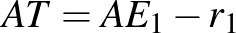 , ezért
, ezért 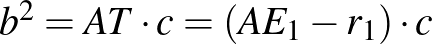 . Átrendezve az összefüggést,
. Átrendezve az összefüggést, 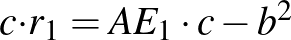 adódik. Ha ezt a (*) egyenletbe behelyettesítjük:
adódik. Ha ezt a (*) egyenletbe behelyettesítjük:
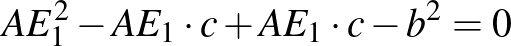
Innen 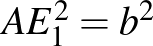 , azaz
, azaz 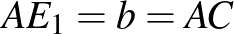 amit bizonyítani akartunk.
amit bizonyítani akartunk.
Hasonlóan bizonyíthatjuk, hogy 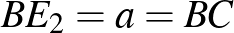 .
.
3. Megoldás inverzióval:
Ennek a megoldásnak az alapötlete Moussong Gábortól (ELTE Geometriai Tanszék) származik.
5. ábra
Tekintsük az 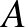 középpontú,
középpontú,  -n átmenő, azaz
-n átmenő, azaz 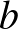 sugarú körre vett inverziót. A befogótétel miatt
sugarú körre vett inverziót. A befogótétel miatt 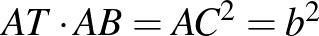 , tehát ennél az inverziónál
, tehát ennél az inverziónál 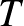 és
és  helyet cserél, és
helyet cserél, és 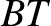 szakasz képe önmaga.
szakasz képe önmaga.
Az inverzió alapkörének minden pontja fix, ezért a  pont képe
pont képe  , ez igaz az
, ez igaz az 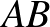 egyenesre vonatkozó
egyenesre vonatkozó 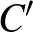 tükörképre is. Ezért a
tükörképre is. Ezért a 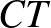 egyenes képe olyan kör, amely az
egyenes képe olyan kör, amely az 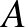 ,
,  ,
, 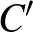 pontokon áthalad, azaz a
pontokon áthalad, azaz a 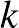 kör. Egy kör képe inverziónál kör vagy egyenes. Akkor lesz egyenes, ha a kör átmegy az inverzió középpontján, így a
kör. Egy kör képe inverziónál kör vagy egyenes. Akkor lesz egyenes, ha a kör átmegy az inverzió középpontján, így a 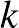 képe a
képe a 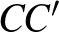 egyenes, azaz a
egyenes, azaz a 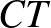 egyenes. Az
egyenes. Az 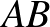 egyenes képe önmaga, mert áthalad az inverzió középpontján.
egyenes képe önmaga, mert áthalad az inverzió középpontján.
A 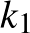 kör képe legyen
kör képe legyen  . Az inverzió érintéstartó transzformáció. A
. Az inverzió érintéstartó transzformáció. A 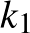 kör érinti az
kör érinti az 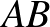 és
és 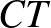 egyeneseket és a
egyeneseket és a 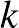 kört, így
kört, így  is érinti ezeket. Ez azt jelenti, hogy
is érinti ezeket. Ez azt jelenti, hogy 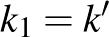 és az
és az 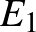 érintési pont az inverziónál fixen marad. Ebből következik, hogy
érintési pont az inverziónál fixen marad. Ebből következik, hogy 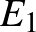 rajta van az inverzió körén,
rajta van az inverzió körén, 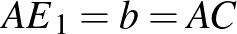 .
.
Megjegyzés:
Ennek a megoldásnak van egy kis hiányossága. Azt mondjuk, hogy a 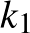 kör és
kör és  kör érinti az
kör érinti az 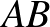 és
és 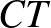 egyeneseket és a
egyeneseket és a 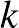 kört, ezért azonosak. Gondoljuk meg, hogy hány ilyen kör van? Ha több is van, akkor miért lesz
kört, ezért azonosak. Gondoljuk meg, hogy hány ilyen kör van? Ha több is van, akkor miért lesz 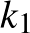 képe önmaga?
képe önmaga?
6. ábra
A 6. ábrán láthatóak ezek a körök. Ha felveszünk a  szögtartományban egy tetszőleges, a
szögtartományban egy tetszőleges, a  és
és 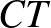 egyeneseket érintő t kört, akkor ebből T középpontú középpontos hasonlósággal egy olyan kört kapunk, ami a
egyeneseket érintő t kört, akkor ebből T középpontú középpontos hasonlósággal egy olyan kört kapunk, ami a 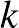 kört belülről és egy olyat, amely kívülről érinti. A többi szögtartományban is két-két megfelelő kör adódik, így 8 kört kapunk.
kört belülről és egy olyat, amely kívülről érinti. A többi szögtartományban is két-két megfelelő kör adódik, így 8 kört kapunk.
Az inverzió az alapkör belsejét a külsejébe képezi le, és viszont. Ezért 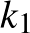 képe valóban önmaga.
képe valóban önmaga.
Mit mondhatunk a többi kör inverz képéről?
A 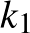 ,
, 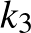 ,
, 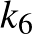 ,
, 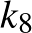 köröket az inverzió önmagukba viszi.
köröket az inverzió önmagukba viszi. 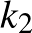 és
és 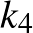 , illetve
, illetve 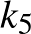 és
és 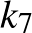 egymás inverzei. (A
egymás inverzei. (A 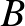 középpontú,
középpontú, 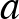 sugarú inverzió esetén az analóg állítások megfogalmazhatóak.)
sugarú inverzió esetén az analóg állítások megfogalmazhatóak.)
Ezek után kíváncsiak lehetünk arra, hogy az OKTV-feladat állítása hogyan változik, ha olyan köröket vizsgálunk, amelyek a 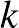 kört kívülről érintik.
kört kívülről érintik.
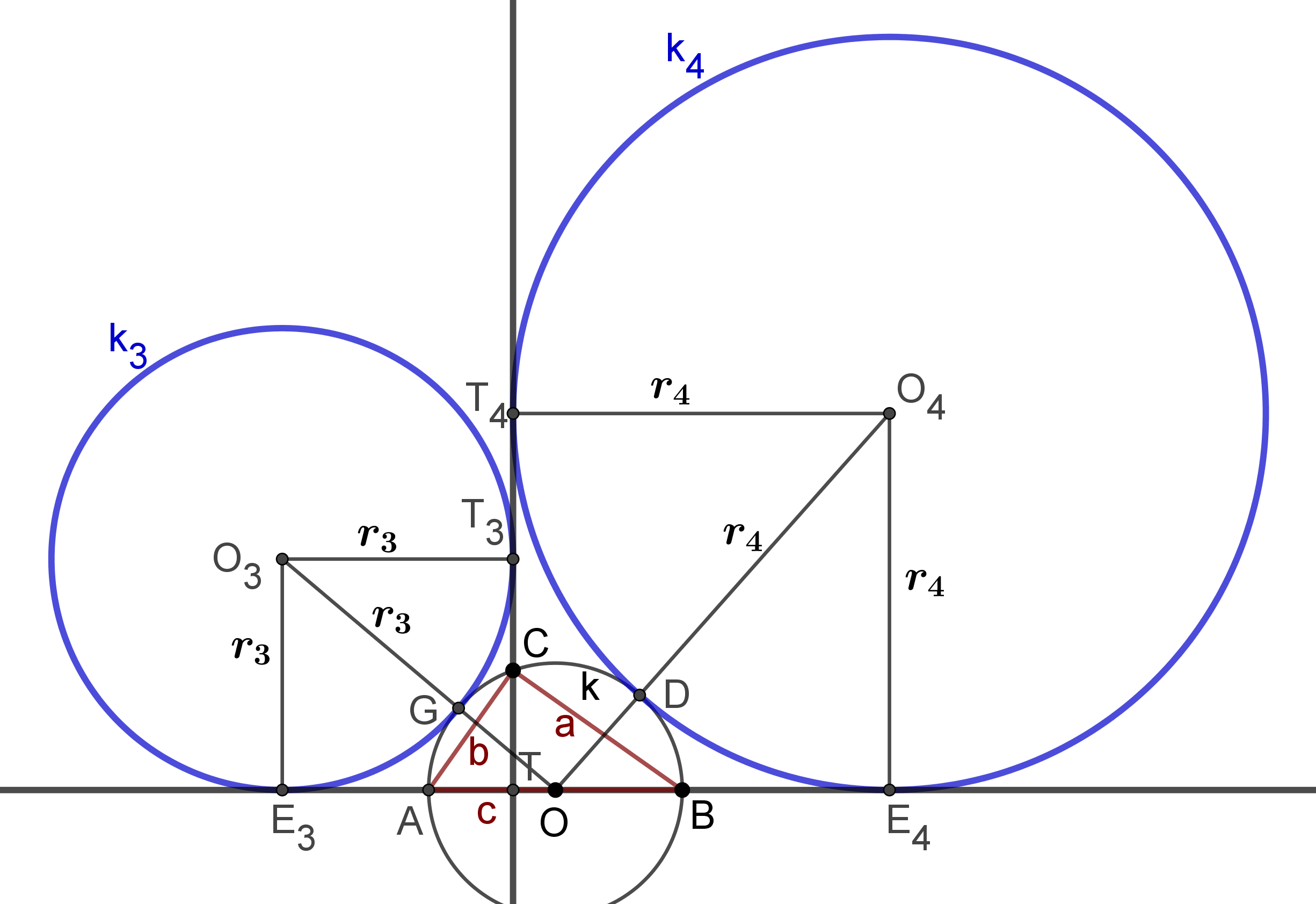
7. ábra
Az 1. megoldás gondolatmenete átvihető a külső érintőkörök esetére, ha belátjuk, hogy A, G, és 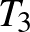 egy egyenesen van.
egy egyenesen van.
A 2. megoldás módszerével így dolgozhatunk (7. ábra):
Számoljuk ki az  szakasz hosszát:
szakasz hosszát:
A belső körökhöz hasonló gondolatmenettel haladva 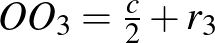 ;
; 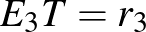 ;
; 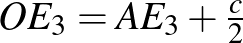 . Az
. Az 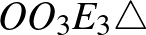 -re felírva a Pitagorasz tételt:
-re felírva a Pitagorasz tételt:

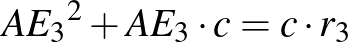 (**)
(**) 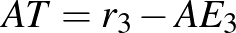 . Felírjuk a befogótételt:
. Felírjuk a befogótételt: 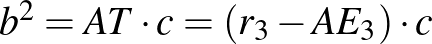 , tehát
, tehát 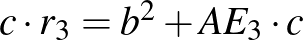 . A (**) egyenletbe helyettesítve:
. A (**) egyenletbe helyettesítve: 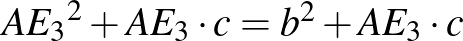 , azaz
, azaz 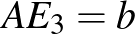 . Hasonlóan kapjuk a
. Hasonlóan kapjuk a 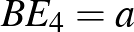 összefüggést. A körök sugarai pedig
összefüggést. A körök sugarai pedig 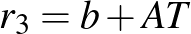 ;
;  .
.
Hogyan bizonyíthatjuk ugyanezt inverzióval?
Az 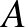 középpontú,
középpontú, 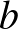 sugarú kört használva a
sugarú kört használva a 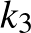 kör inverz képe önmaga, az
kör inverz képe önmaga, az 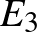 pont fixpont, tehát
pont fixpont, tehát 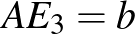 . A
. A 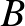 középpontú,
középpontú, 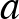 sugarú kört használva
sugarú kört használva 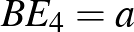 .
.
Érdekes kérdés, hogy milyen pont az 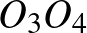 szakasz felezőpontja…
szakasz felezőpontja…
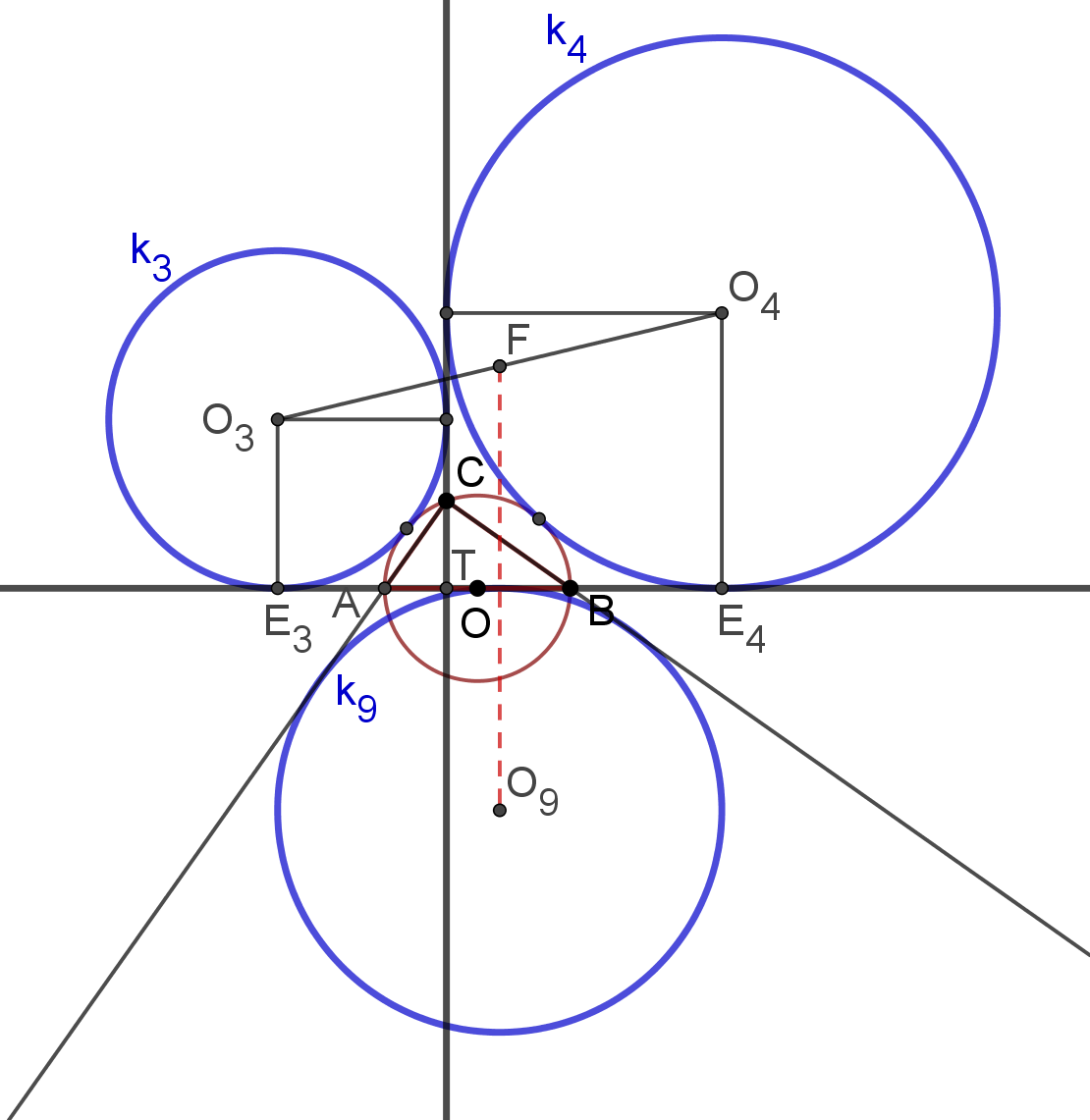
8. ábra
A fentiekből az első megoldásban leírtakkal analóg módon adódik, hogy ha az 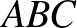 háromszög
háromszög 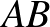 oldalát kívülről érintő kör középpontját
oldalát kívülről érintő kör középpontját 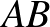 -re tükrözzük, akkor az
-re tükrözzük, akkor az 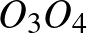 szakasz felezőpontját kapjuk.
szakasz felezőpontját kapjuk.
Kempelen Farkas Gimnázium
ELTE Algebra és Számelmélet Tanszék









