Matematikaoktatás online – tudunk-e újat az előző félévhez képest?

1. Bevezetés

A COVID-19 járvány miatt a BME Gazdaság- és Társadalomtudományi Karának hallgatói a 2020/21-es tanév őszi félévében rögtön a legelejétől távoktatásban kezdték tanulni a matematikát. Az előző félévhez hasonlóan a szinkron online oktatást céloztuk meg úgy, hogy lehetővé tettük az előadások, gyakorlatok és konzultációk felvételeinek visszanézését már csak azért is, mert az általunk használt platform (Microsoft Teams) egyszerre maximum 360 főnek engedélyezte az előadások értekezleteibe történő csatlakozást, elsőéves hallgatóink létszáma pedig meghaladta az 500-at. A valós időben (Microsoft Teamsen) megtartott kis létszámú gyakorlatokon való aktív online részvételt viszont erősen ajánlottuk minden olyan hallgatónknak, aki ezt megtehette.

A kommunikációs csatornák és a rendelkezésünkre álló online platformok kiválasztásában az előző félévben már szereztünk némi tapasztalatot [1], az ott elkövetett kezdeti hibákból valamennyit már okultunk, így jóval több időnk szabadult fel az online számonkérések és az interaktív válaszadó rendszerek előkészítésére, amire a nagy hallgatói létszám miatt a korábbinál is jóval nagyobb szükségünk volt. Nekünk, oktatóknak most már nem a tanév zökkenőmentes lezárása volt a cél, ennél jóval többet szerettünk volna megvalósítani [2].

2. Számonkérés a matematikaoktatásban: áttérés a Moodle-tesztekre

Mivel Microsoft Teamsben 200 fő fölötti csoportokban nagyon körülményes munkát (feladatot, tesztet) kiosztani, számonkérni és értékelni, és ebben a félévben a nemzetközi gazdálkodás, pénzügy és számvitel, valamint gazdálkodási és menedzsment alapszakos hallgatóink 530-an, azaz kb. kétszer annyian vették fel a matematika tárgyat, mint az előző félévben, a számonkérések lebonyolításán mindenképpen változtatnunk kellett. Így mind a zárthelyi dolgozatokat, mind pedig az írásbeli vizsgákat Moodle-tesztek formájában írattuk meg.

Egy Moodle-teszt íratásakor számos kockázatot vállalunk, ezek közül a legaggasztóbb az, amikor a kevésbé felkészült, de elszánt hallgatók Discord-szobákban vagy egyéb helyeken hosszasan keresik a tesztjeikben megtalálható azonos feladatokat. Mivel Moodle-tesztjeinkben nem kértük a teljes feladatmegoldások kézzel írt másolatának csatolását, csupán a részfeladatok eredményeivel kapcsolatos helyes válaszok megjelölését, figyelembe kellett vennünk azt, hogy lehetnek majd olyan hallgatóink, akik az írásbeli tesztek ideje alatt más platformok igénybevételével sok időt fordítanak tesztfeladataik összehasonlítására, közös tesztkérdések és válaszok keresésére. Minden felmérésben a feladatok sokszínűségével, változatos kérdéscsomagokkal igyekeztünk arra ösztönözni a hallgatókat, hogy minden idejüket az egyéni munkára fordítsák és eszükbe se jusson más dolgokkal foglalkozni, ha jó eredményt szeretnének elérni a teszteken. Annyi feladatot tartalmazott egy-egy ilyen Moodle-teszt, hogy csak folyamatos számításokkal és munkával lehetett teljesíteni. Emiatt rengeteg időnket vitte el a meglehetősen nagy volumenű Moodle-feladatbankunk előállítása. A Moodle-zárthelyik és írásbeli vizsgák több jó válaszos feladatokból álló tesztek voltak, melyek feladatai a feladatbank kategóriáiból (ugyanolyan típusú feladatokat tartalmazó feladatcsomagjaiból) véletlenszerűen lettek kiválasztva, és melyekben a helytelen válaszok kiválasztásáért negatív pontszám járt. Egy teljes függvényvizsgálattal kapcsolatos feladat például a következőképpen nézhetett ki:

Tekintse az 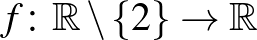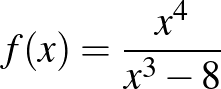$f\colon \mathbb{R}\setminus \{2\}\to \mathbb{R}$ , $f(x)=\dfrac{x^4}{x^3-8}$ függvényt! Válassza ki az összes igaz állítást:

a) 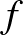$f$ páros függvény.

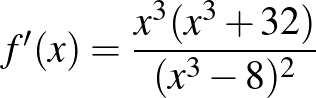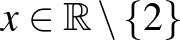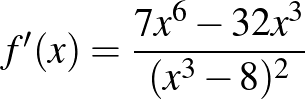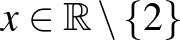b) $f'(x)=\dfrac{x^3(x^3+32)}{(x^3-8)^2}$ , $x\in \mathbb{R}\setminus \{2\}$ .

c) $f'(x)=\dfrac{7x^{6}-32x^3}{(x^3-8)^2}$ , $x\in \mathbb{R}\setminus \{2\}$ .

d) Az 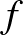$f$ függvény zérushelye lokális minimumhely is egyben.

e) Az 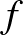$f$ függvénynek pontosan három stacionárius pontja van.

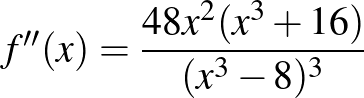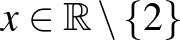f) $f''(x)=\dfrac{48x^2(x^3+16)}{(x^3-8)^3}$ , $x\in \mathbb{R}\setminus \{2\}$ .

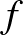g) Ha $x\in \left(-\infty,-\sqrt[3]{16}\right)$ , akkor az $f$ függvény konvex.

h) Az 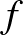$f$ függvénynek 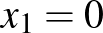$x_1=0$ inflexiós pontja.

i) Ha 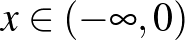$x\in (-\infty,0)$ , akkor az 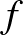$f$ függvény szigorúan monoton növekvő.

j) Az 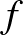$f$ függvény nem csak a 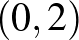$(0,2)$ intervallumon szigorúan monoton csökkenő.

k) $x\in \left(\sqrt[3]{32},\infty \right)$ esetén az 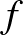$f$ függvény deriváltfüggvénye pozitív.

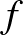l) Az $x_2=\sqrt[3]{32}$ az $f$ függvény egyetlen lokális minimumhelye.

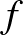m) Az $x_3=-\sqrt[3]{16}$ az $f$ függvény egyetlen inflexiós pontja.

n) Az 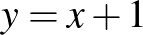$y=x+1$ egyenes aszimptotája az 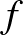$f$ függvénynek 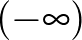$(-\infty)$ -ben is és ∞-ben is.

o) Nem válaszolok.

E cikk írásának idején az őszi félév teljes terjedelmében még nem bontakozott ki, hiszen az öt vizsgaalkalomból még csak három zárult le az, érhetnek még meglepetések bennünket. Az eddig lezajlott három vizsga átlaga nem sokban különbözik a tavaszi vizsgaátlagoktól, amikor a kisebb hallgatói létszám miatt bevállaltuk a feladatmegoldások teljes javítását.

3. A segédanyagokról röviden

Már az előző félévben bevált, és a hallgatók visszajelzéseiből is egyértelmű volt, hogy ebből a tárgyból is szükséges minden egyes előadás és gyakorlat magyarázatokkal tarkított, részletes tananyagát elkészíteni és már a tanórákat megelőző napokban elérhetővé tenni mind a Teams-fájlok között, mind pedig az oktató személyes honlapján. Ezzel remélhetőleg sok hallgatót tudtunk motiválni a tanulásban, mert lehetett akár előre tanulni, készülni minden előadásra és gyakorlatra. Ezáltal az órák is interaktívvá váltak, mert egyes hallgatók a tananyag előzetes átolvasásával bátrabban mertek kérdéseket feltenni, megválaszolni, vagy akár egyéb feladatmegoldásokat javasolni.

Azt, hogy milyen részletesen kell az órákon magyarázni, mindig a hallgatók matektudása határozza meg. Erre már az első előadáson rákérdeztünk Mentimeter segítségével. Olyan kérdésekre kellett válaszolniuk például, hogy milyen szintű érettségit tettek matematikából és mennyire félnek az előttük álló (első féléves) matematika számonkérésektől, ezzel is arra buzdítva őket, hogy már az elejétől kezdve aktívak legyenek az órákon. Az első kérdésünkre 426 válasz érkezett (ábra):

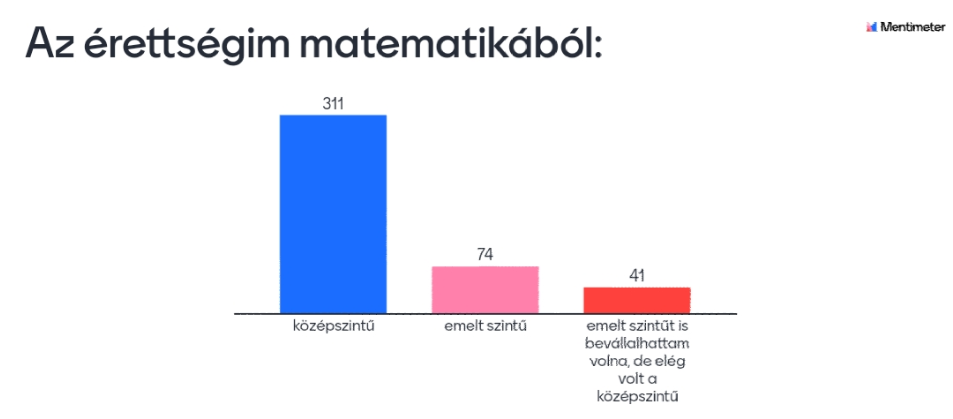
Ebből az eredményből azonnal tudtuk, hogy hallgatóinknak alapos magyarázatokra, rengeteg tanulásra és aktív online részvételre ösztönző, motiváló gesztusra van szüksége ahhoz, hogy következetesen és lelkiismeretesen végigtanulják a félévet: például az órákon feltett okos hozzászólásokat, valamint a megadottól eltérő helyes feladatmegoldásokat bónuszpontokkal jutalmaztuk, melyeket a vizsgán lehetett beváltani.

A feltöltött oktatási segédanyagaink mellett a féléves anyagot teljesen lefedő Egyváltozós valós függvények interaktív Neptun e-tananyagunk is hallgatóink rendelkezésére állt. Ez a tananyag érdekes ábráival és animációival, interaktív feladatmegoldásaival és tesztjeivel lépést tart a mai igényekkel. Minta Moodle-zárthelyiket, valamint minta vizsgatesztet is hallgatóink rendelkezésére bocsájtottunk, hogy ellenőrizhessék tudásukat a számonkérések előtt. Ezek elkészítése sok időnket elvitte, de hasznosnak bizonyultak.

4. A vizsgajegyek kialakításáról

Aki az írásbeli vizsga után legalább közepes vizsgaeredményt ér el, részt vehet egy 3 tesztkérdésből álló opcionális, rövid, online szóbeli vizsgán, amit a Teamsen bonyolítunk le és amihez kamerát is használunk. Ezen egy jeggyel lehet változtatni az írásbeli vizsga eredményén (így akár rontani is lehet), és itt minden kérdés a fent említett Neptun-tananyagnak a (többnyire elméleti) tesztjeiből van összeválogatva.

Érdekes és számunkra kissé lehangoló, hogy hallgatóink a szóbeli helyett inkább a teljes írásbeli vizsga újraírását célozzák meg. Ennek hátterében az lehet, hogy ezen a szóbelin a tételek, definíciók nagyon pontos visszakérdezése történik, ami a hallgatók szerint jóval több stresszel és felkészüléssel jár, mint a félévben tanult feladattípusok begyakorlása.

Ebben a távoktatásban töltött félévben is nagyon hiányoltuk a tantermi oktatás általános hangulatát, izgalmát és millőjét. Véleményünk szerint az online oktatás egyelőre nem ér fel a hagyományos tantermi oktatással, de egy jól strukturált, könnyen követhető tárgykövetelményekkel, játékszabályokkal lejátszott, átlátható online oktatási folyamat, valamint a benne tanúsított kölcsönös bizalom és empátia valamelyest kárpótol bennünket az elveszített tantermi tanítási élményekért.

Végezetül, évek múltán könnyen lehet, hogy az oktatási tartalmakra csak halványan emlékeznek majd hallgatóink, de nem felejtik el azt, hogy mit éreztek ezekben a hónapokban, emlékeznek majd arra, hogyan törődtünk velük és hogyan támogattuk őket [3].

Irodalomjegyzék

: [1] https://ematlap.hu/tanora-szakkor-2020-12/1006-az-online-matematikaoktatas-tapasztalatai-oktatoi-es-hallgatoi-szemmel

[2] „Digitális kompetenciáinkat erősíti a távolléti oktatás” – Budapesti Műszaki és Gazdaságtudományi Egyetem

[3] Bozkurt, A., Sharma, R. C. (2020). Emergency remote teaching in a time of global crisis due to CoronaVirus pandemic, Asian Journal of Distance Education, 15, i-vi.

Fülöp Ottilia

BME Matematika Intézet, Differenciálegyenletek Tanszék

A szerkesztő megjegyzése. Az online számonkérésről két további cikket olvashatnak ugyanebben a számban, egyik a Debreceni Egyetem oktatóinak tapasztalatait foglalja össze, a másik egy fiatal középiskolai tanár ötletének megvalósítását.