1. Bevezetés
A 2020 júniusi Érintőben megjelent „Hány bőrt lehet lehúzni egy feladatról? – avagy nincs új a Nap alatt?” című cikkben szóba került egy feladat, amely az ELTE TTK matematika tanár szakosok tananyagában is szerepel ([Fried, K. (2020).]).
A tananyag folyamatos frissen tartása érdekében az oktatók rendszeresen tanulmányozzák a diákok nehézségeit, feladatokhoz való hozzáállását és a megoldásaikat. Ebben a tanulmányban az ELTE TTK Matematikatanítási és Módszertani Központ két oktatója mutat be egy válogatást az említett feladathoz készíthető megoldásokból, hallgatói munkákat is felhasználva. Bár olykor csak az ötletig jutottak el a hallgatók, a teljes megoldást nem sikerül megtalálniuk, de ez semmit sem rontott az ötlet felhasználhatóságán.
Érdekes a gyakorlatokon megfigyelni, hogy miként változnak az egyetemi diákok feladatokra adott megoldásai attól függően, hogy milyen előtanulmányokat folytattak, hogyan állnak a geometriához, illetve hogy a kiadott feladatsor feladatait milyen sorrendben dolgozzák fel. Fontos tapasztalat az is, hogy a hallgatót jól be lehet vonni a munkába, ha a saját gondolataira építhet, ezeket kiegészítheti, viszont ha ettől eltérő, „idegen” ötletet kap, előfordul, hogy azt a megközelítést elutasítóan fogadja.
A most következő íráshoz tehát hallgatói munkákból, megoldásokból, ötletekből szemezgettek a szerzők, és az egyes megoldásokhoz megjegyzéseket fűztek, illetve rendezték, helyenként ki is egészítették ezeket.
2. Miért is foglalkozunk ezzel a témával?
Egy geometriai problémához készült megoldások vizsgálata számos lehetőséget rejt magában. A megoldások átgondolása és rendezése például újabb megoldási ötletekhez vezethet. De a különböző megoldások jellege, mennyisége a megoldó geometriai gondolkodásáról is szolgálhat többféle, esetleg mérhető felvilágosítással [Levav, A. & Leikin, R. (2010).]. Meggondolható az a lehetőség is, hogy figyelembe véve az egyes megoldások ismereti-gondolkodásbeli szintjét, különböző évfolyamokon is elővehető ugyanaz a feladat, és akár több éven át is gyűjthetők hozzá megoldások, ami segíthet egyben az oktatásban sajnos eléggé uralkodó „egy feladat-egy megoldás” hozzáállás ellen is hatni. Ha egy problémához több megoldás áll a tanár rendelkezésére, akkor válogathat is belőlük olyanokat, amelyekhez ötletadó segítséget adva, a matematikában kevésbé teljesítőképes tanuló is megoldást tud készíteni. Itt természetesen arra törekedve, hogy a segítő ötlethez (például ábrához) több lehetséges megoldás is készíthető legyen [Ambrus, G. & Rott, B. (2017).].
Egy problémákhoz készült/gyűjtött megoldások rendezhetők például aszerint, hogy a problémamegoldó milyen matematikai eszközöket használt a megoldásokhoz és azok hogyan függnek össze ([Levav, A. & Leikin, R. (2010)., Fig2.]). Egy ilyen jellegű rendezést szeretnénk végül bemutatni a feladatunk megoldásai esetében, jelölve benne, hogy egy általunk megfigyelt hallgató megoldásai melyik megoldással egyeznek meg lényegileg. A megoldások első rendezésének alapja lehetne egy hallgató ötleteinek követése is, és megpróbálhatnánk ebbe beilleszteni a további megoldásokat. A következőkben ettől eltérő utat választottunk. A megoldások rendezése valójában egy láncolat alapján történik, amelyhez a főbb láncszemeket mi határoztuk meg a gyűjtött megoldásaink ismeretében; a láncszemekhez tartozó főbb (ötletek) gondolatok:
– felmérjük egy szakaszra két szakasz összegét
– geometriai transzformációk használata
– trigonometriai számítás, tételek
– algebraizálás (koordinátageometriai eszközök igénybevétele)
A továbbiakban először bemutatjuk a – most már sokat emlegetett – feladatot, majd következnek a megoldások (az említett lánc szerint rendezve). Mindegyik megoldás bemutatása előtt megemlítjük a felhasznált főbb ismereteket, matematikai eszközöket és azt a szemléleti kérdést, hogy a megoldáshoz a feladat ábráján belül elég volt-e dolgozni, vagy ki kellett-e lépni belőle, vagyis az esetleges belső ábra kiegészítésein kívül szükség volt-e az ábrához külső kiegészítésre. (Ez utóbbinak az elemzése is érdekes kérdés lenne, de ezzel most nem foglalkozunk.) A megoldások mellett helyenként egy kék szám található, ez azt jelzi, hogy egy, az általunk figyelt hallgatónál ([Tóth E. (2009).]) ez a megoldás (lényegileg így) hányadikként jelent meg.
Ezután kerül sor a megoldások végső áttekintő rendezésére egy ábra segítségével, a felhasznált matematikai eszközök alapján a már korábban elmondottak szerint.
Annak érdekében, hogy a megoldások között fennálló kapcsolatot jobban láttassuk, több megoldáshoz is lényegében ugyanazt az ábrát illesztettük be a most következő megoldásoknál.
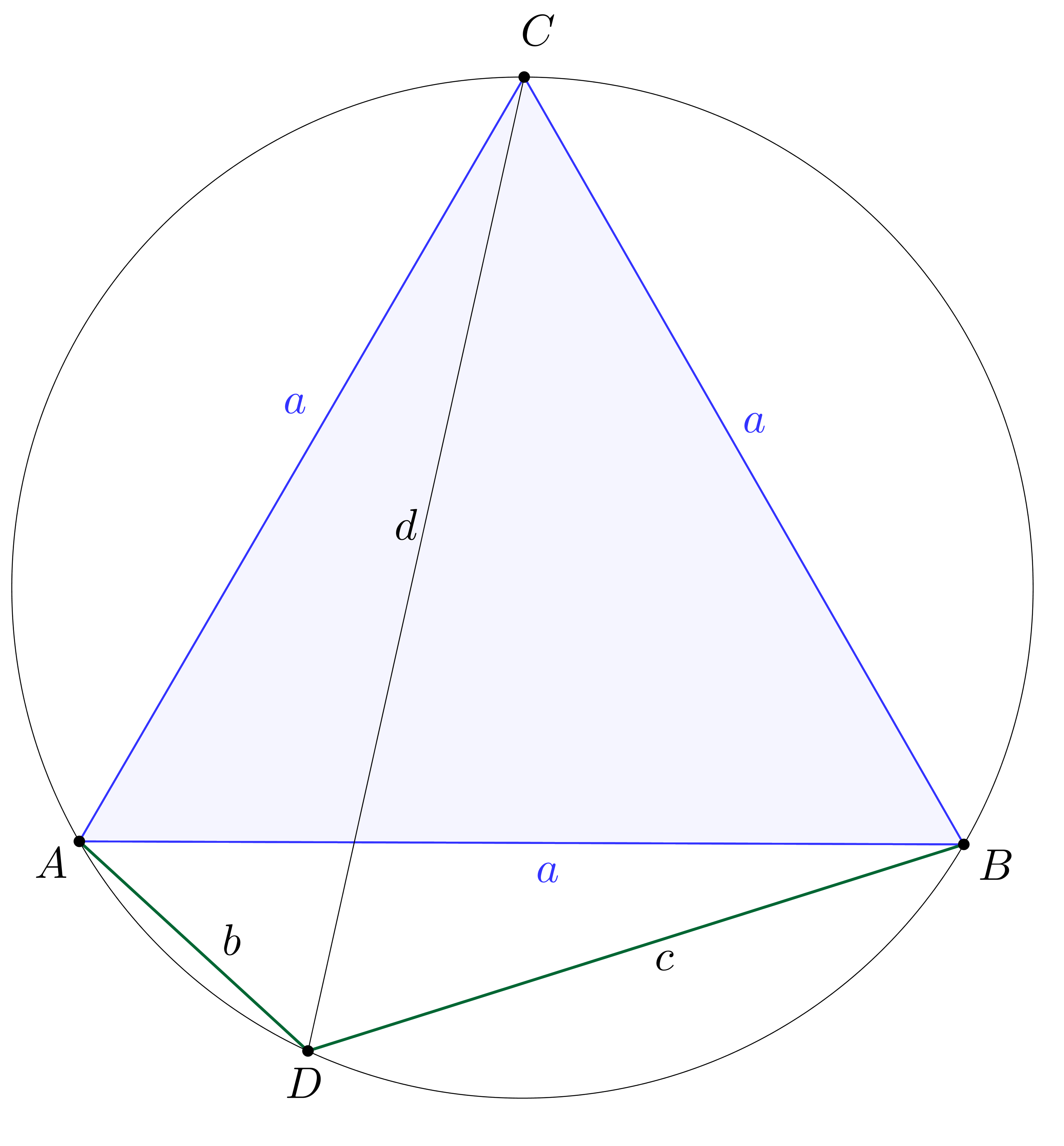
A feladat. Az 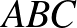 szabályos háromszög körülírt körén, a rövidebbik
szabályos háromszög körülírt körén, a rövidebbik 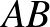 íven felvesszük a
íven felvesszük a 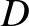 pontot. Igazoljuk, hogy
pontot. Igazoljuk, hogy 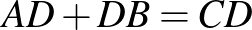 !
!
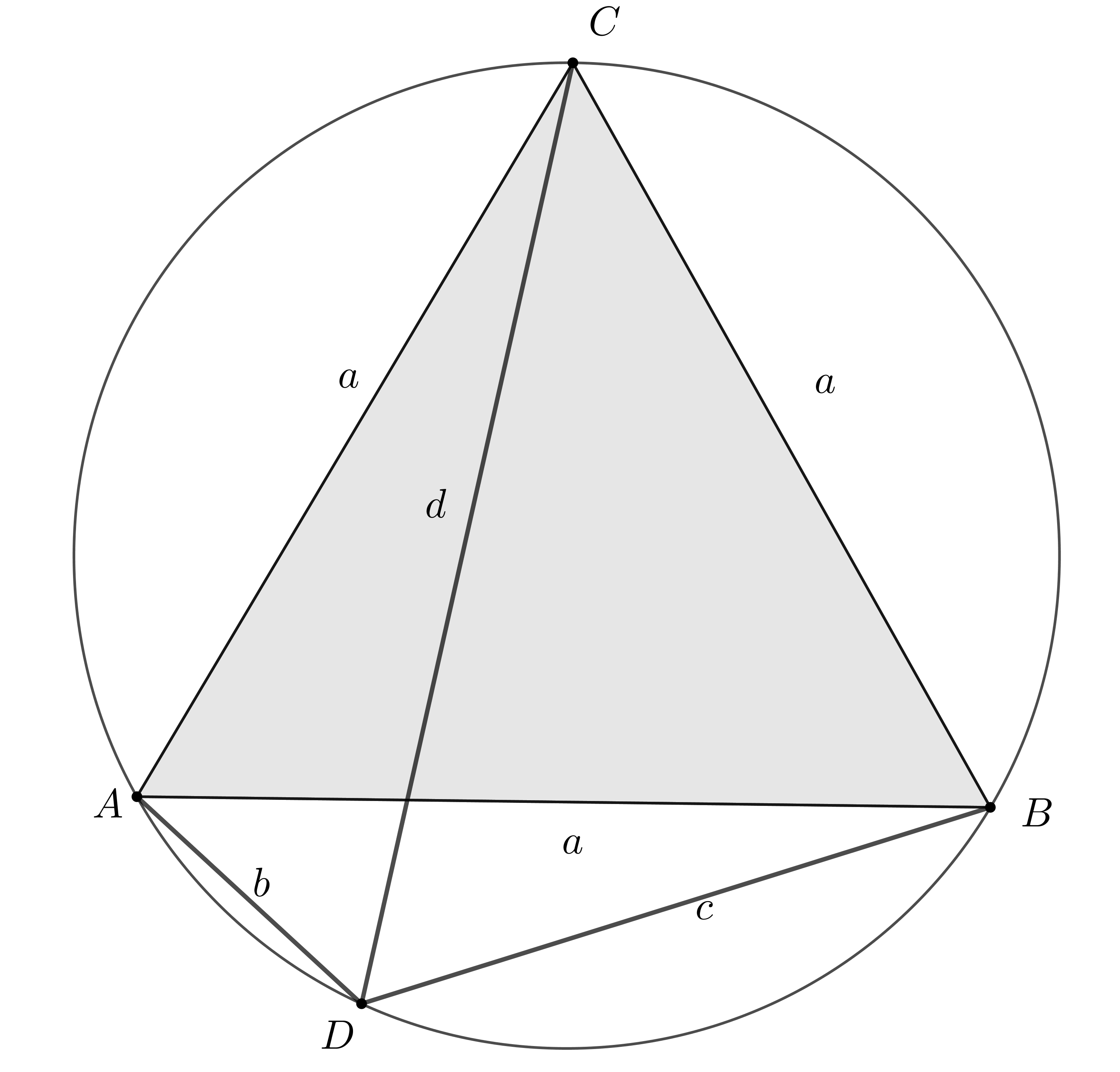
A feladathoz tartozó megoldásláncunk:
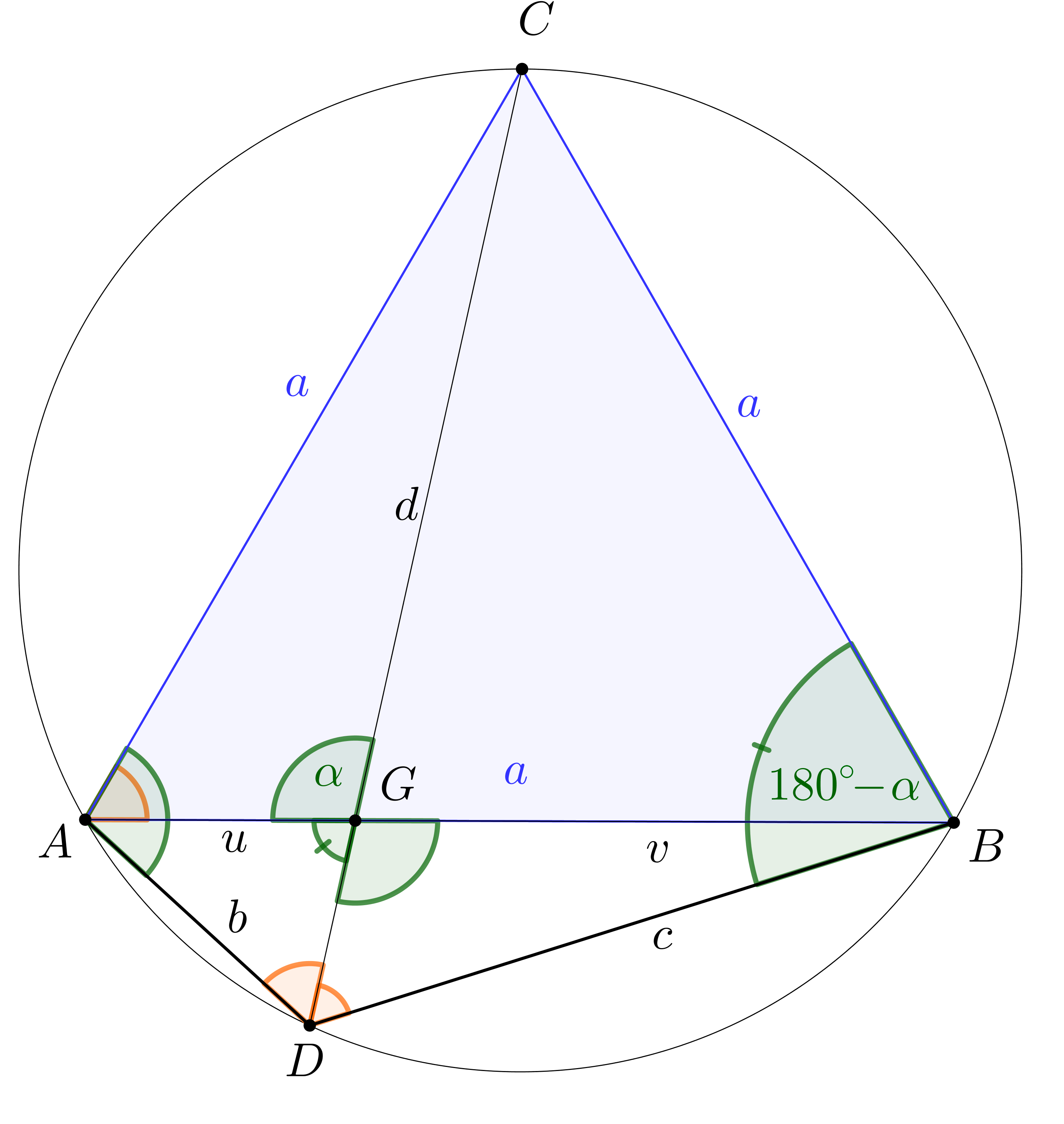
1. megoldás (1. megoldás (a) variáció) – szakaszok összege egy szakaszon (5)
– alapötlet: szakaszok összege egy szakaszon, szakasz meghosszabbításán
– bizonyítás alapja: egybevágóság (transzformáció), kerületi szögek
– szemlélet: „kifelé” dolgozunk az eredetileg a feladathoz készült ábrából.
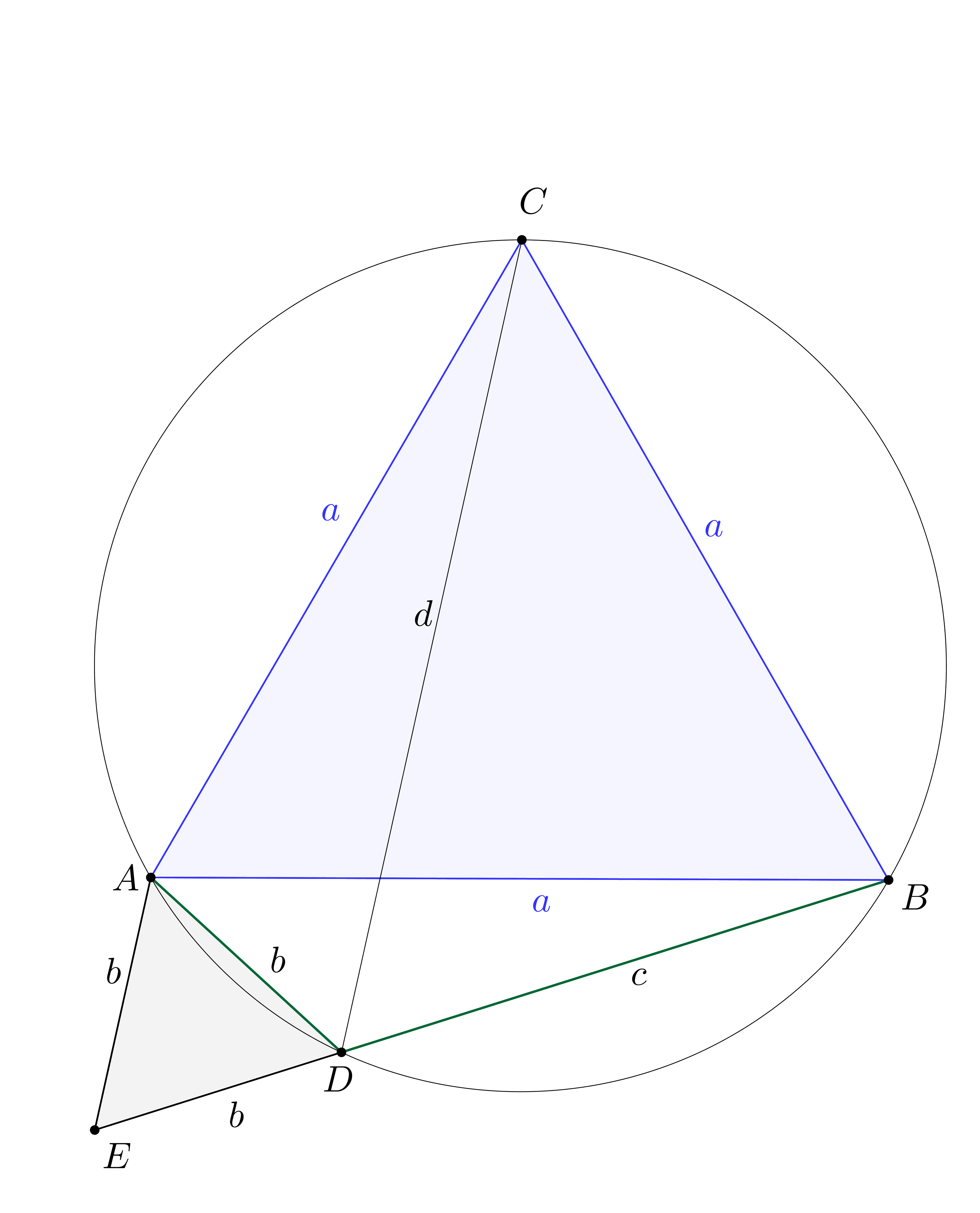
Mérjük fel a 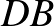 szakaszra
szakaszra  -n túl az
-n túl az 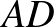 szakaszt (
szakaszt (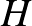 ).
).

Az 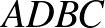 húrnégyszög, ezért
húrnégyszög, ezért 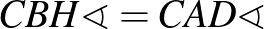 (mindkettő
(mindkettő  -ra egészíti ki a
-ra egészíti ki a 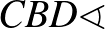 -et).
-et). 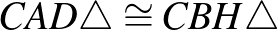 , mert két-két oldaluk egyenlő hosszú, és az általuk közbezárt szög ugyanakkora. Ebből következik, hogy a harmadik oldalaik is egyenlők:
, mert két-két oldaluk egyenlő hosszú, és az általuk közbezárt szög ugyanakkora. Ebből következik, hogy a harmadik oldalaik is egyenlők: 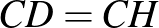 , a
, a 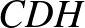 háromszög egyenlő szárú. Mivel a
háromszög egyenlő szárú. Mivel a 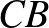 ívhez tartozó
ívhez tartozó 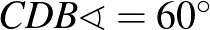 -os, így a
-os, így a 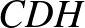 háromszög szabályos is. Innen
háromszög szabályos is. Innen 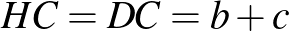 .
.
A megoldást megelőző, korábbi feladatmegoldásokból leszűrt ötlet: két szakasz összegét úgy lehet más szakasz hosszával összehasonlítani, ha egy egyenesre (csatlakozva) vesszük fel a két szakaszt. Ez a gondolat kerül alkalmazásra a további három megoldásban is, csak módosított változatban.
2. megoldás (1. megoldás (b) variáció) – szakaszok összege egy szakaszon (4)
– alapötlet: szakaszok összege egy szakaszon, szakasz meghosszabbításán
– bizonyítás alapja: egybevágóság (transzformáció), kerületi szögek
– szemlélet: „kifelé” dolgozunk
Hosszabbítsuk meg 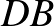 -t
-t 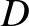 -n túl, és mérjünk fel rá az
-n túl, és mérjünk fel rá az 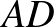 hosszú szakaszt. Így kapjuk az
hosszú szakaszt. Így kapjuk az 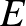 pontot. Ezt az
pontot. Ezt az 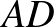 szakasz
szakasz 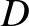 körüli
körüli 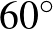 -os elforgatásával is megkaphatjuk. Ezek szerint
-os elforgatásával is megkaphatjuk. Ezek szerint 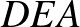 szabályos háromszög (két oldala egyenlő hosszú és
szabályos háromszög (két oldala egyenlő hosszú és 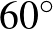 -os szöget zár be).
-os szöget zár be).
Az 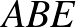 és
és  háromszögek szögei páronként egyenlőek:
háromszögek szögei páronként egyenlőek: 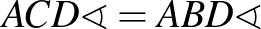 (az
(az 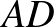 húrhoz tartozó kerületi szögek),
húrhoz tartozó kerületi szögek), 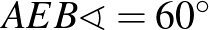 , mert
, mert  szabályos, továbbá
szabályos, továbbá 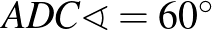 , mert az
, mert az  ívhez tartozó kerületi szög.
ívhez tartozó kerületi szög.
 és
és  tehát hasonlók, de egybevágók is, mert a
tehát hasonlók, de egybevágók is, mert a 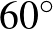 -os szögükkel szemközti oldalaik egyaránt
-os szögükkel szemközti oldalaik egyaránt 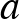 hosszúságúak.
hosszúságúak.
Ebből következik, hogy harmadik oldalaik is egyenlők:  , azaz
, azaz 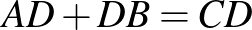 .
.
3. megoldás – szakaszok különbsége
– alapötlet: szakaszok különbsége egy szakaszon, szakasz meghosszabbításán
– bizonyítás alapja: egybevágóság (transzformációval vagy anélkül), kerületi szögek
– szemlélet: „befelé” dolgozunk.
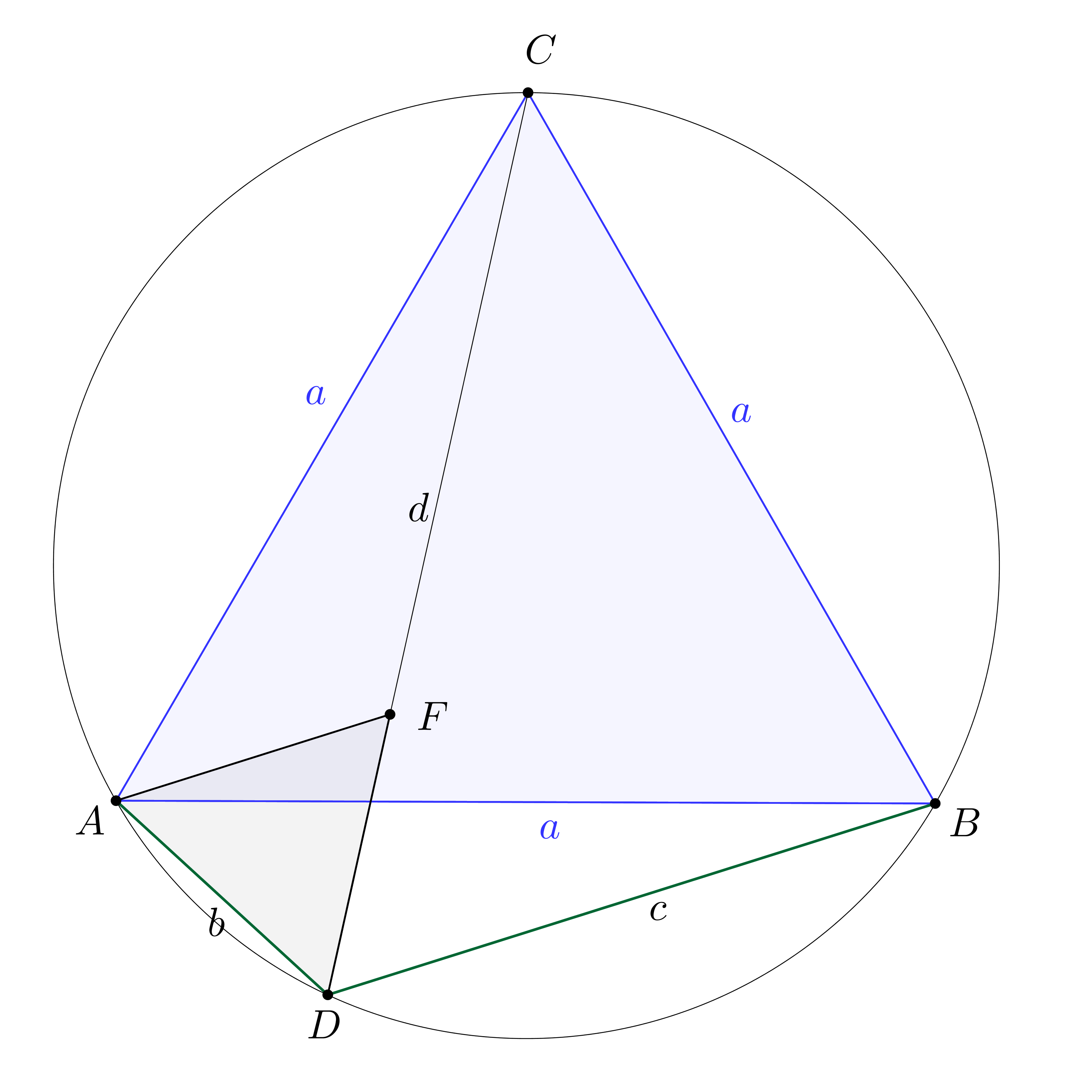
Mérjük fel a 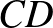 szakaszra
szakaszra 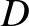 -ből a
-ből a 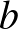 (
(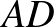 ) távolságot. Így kapjuk az
) távolságot. Így kapjuk az 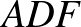 egyenlő szárú háromszöget, de mivel a szárszöge,
egyenlő szárú háromszöget, de mivel a szárszöge, 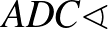 az
az 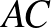 húrhoz tartozó kerületi szög
húrhoz tartozó kerületi szög 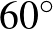 -os, a háromszög szabályos is.
-os, a háromszög szabályos is.
Belátjuk, hogy 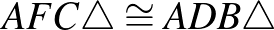 , amiből már következik, hogy
, amiből már következik, hogy 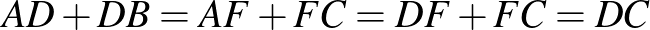 .
.
A két háromszög hasonló, mert egyenlők a szögei: az 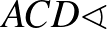 és az
és az 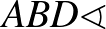 az
az 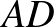 ívhez tartozó kerületi szögek, tehát egyenlők; az
ívhez tartozó kerületi szögek, tehát egyenlők; az 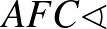
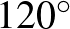 -os, hiszen a
-os, hiszen a 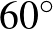 -os
-os 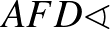 kiegészítő szöge, továbbá az
kiegészítő szöge, továbbá az  is
is 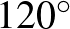 -os, mert
-os, mert 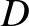 az
az 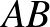 húr
húr  -t nem tartalmazó ívén helyezkedik el és
-t nem tartalmazó ívén helyezkedik el és 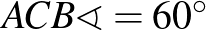 .
.
Mivel a két hasonló háromszögben a legnagyobb oldalaikkal szemközti (leghosszabb) oldalaik egyenlő hosszúak (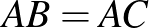 ), így a két háromszög egybevágó.
), így a két háromszög egybevágó.
(Valójában azt kaptuk meg eredményül, hogy 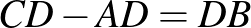 .)
.)
4. megoldás – szakaszok összege egy szakaszon
– alapötlet: szakaszok összege egy szakaszon, hozzáírt szabályos háromszög
– bizonyítás alapja: egybevágóság (transzformáció), kerületi szög
– szemlélet: „kifelé” dolgozunk
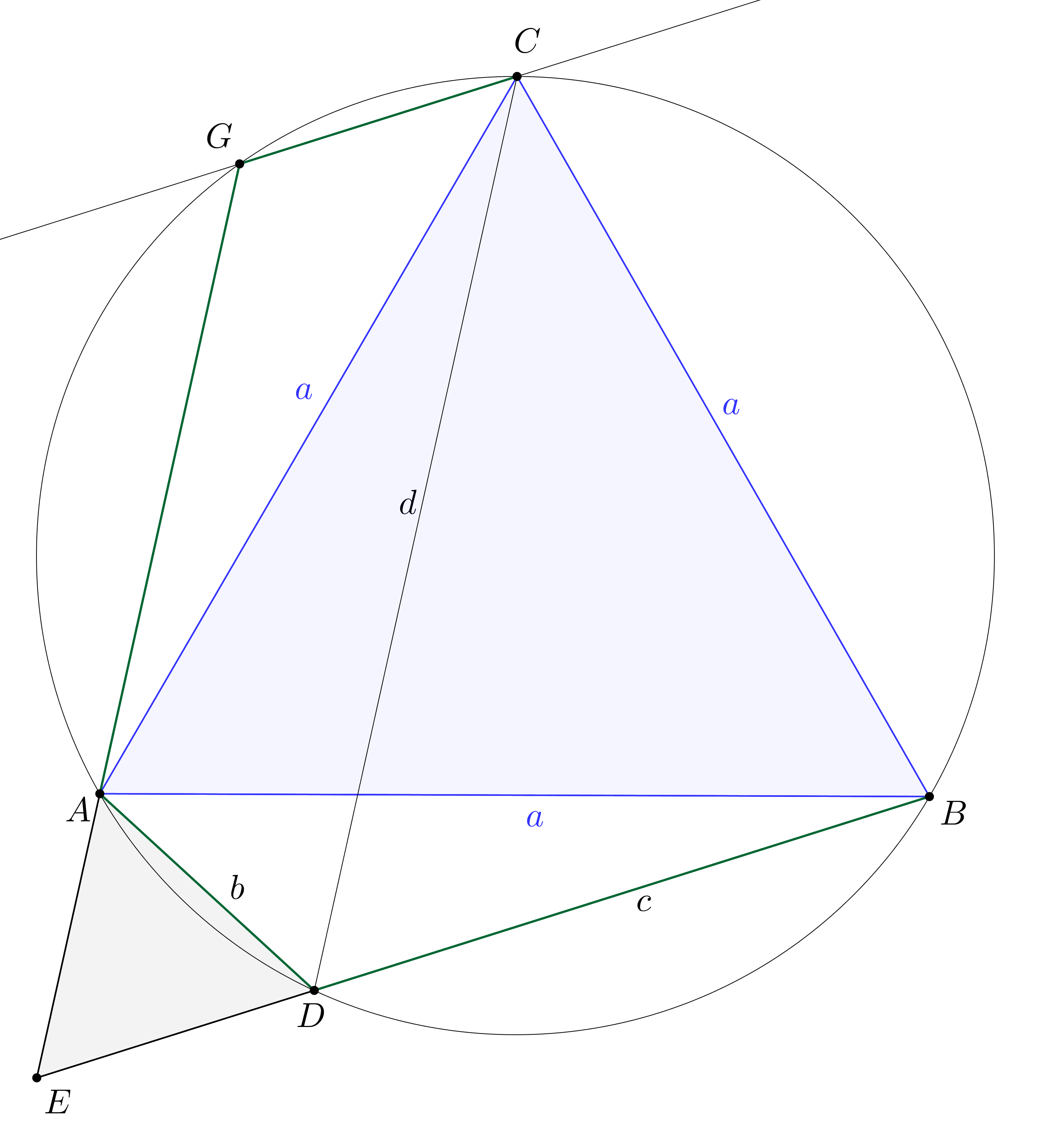
Ha meghosszabbítjuk a 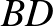 szakaszt
szakaszt  -n túl, az
-n túl, az 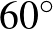 -os szöget zár be az
-os szöget zár be az 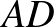 oldallal, mert az
oldallal, mert az 
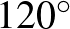 -os, hiszen az
-os, hiszen az 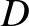
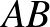 húrhoz tartozó
húrhoz tartozó  -vel átellenes ívén van. Felmérve
-vel átellenes ívén van. Felmérve 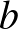 -t a meghosszabbítással kapott félegyenesre
-t a meghosszabbítással kapott félegyenesre 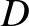 -n túl, az
-n túl, az 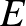 pontot kapjuk. AZ
pontot kapjuk. AZ  háromszög szabályos, mert
háromszög szabályos, mert 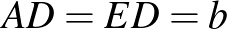 , és
, és 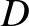 -nél
-nél 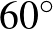 -is szöge van. Jelölje az
-is szöge van. Jelölje az 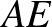 egyenes körrel vett metszéspontját
egyenes körrel vett metszéspontját 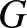 .
.
Mivel az 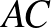 ívhez tartozó
ívhez tartozó 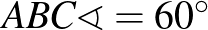 , így
, így 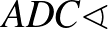 is
is 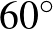 -os, innen
-os, innen 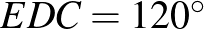 . Továbbá
. Továbbá 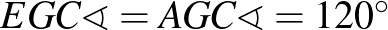 , mert
, mert 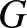 az
az 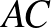 húrhoz tartozó rövidebbik íven van.
húrhoz tartozó rövidebbik íven van.
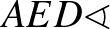
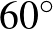 -os, így az
-os, így az 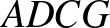 négyszögben a negyedik szög,
négyszögben a negyedik szög, 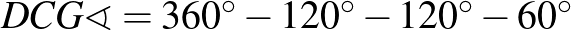 is
is 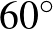 -os. Eszerint
-os. Eszerint  paralelogramma.
paralelogramma.
Ebből következik, hogy 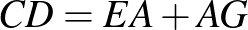 . Tehát be kell látnunk, hogy
. Tehát be kell látnunk, hogy 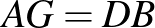 . Az
. Az  és
és 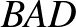 háromszögek egybevágók, mert
háromszögek egybevágók, mert 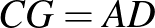 ,
,  és az
és az 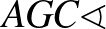 és
és  szögek is egyenlően,
szögek is egyenlően, 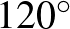 -osak. A legnagyobb szöggel szemközti oldalaik egyenlő hosszúak (
-osak. A legnagyobb szöggel szemközti oldalaik egyenlő hosszúak (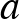 ).
).
(A megoldás több állítása is megmutatható más módon is. Például  úgy is belátható, hogy a kör középpontja körüli
úgy is belátható, hogy a kör középpontja körüli 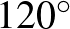 -os forgatás
-os forgatás  -t
-t 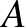 -ba,
-ba, 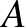 -t
-t  -be és a
-be és a 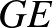 egyenesét olyan, az
egyenesét olyan, az  egyenesével megegyező állású egyenesbe viszi, amelynek
egyenesével megegyező állású egyenesbe viszi, amelynek 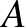 pontja a
pontja a  -be megy, vagyis az
-be megy, vagyis az  egyeneséről van szó. Ezért ez a forgatás
egyeneséről van szó. Ezért ez a forgatás 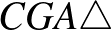 -et az
-et az 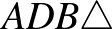 -be viszi.)
-be viszi.)
Ezek szerint 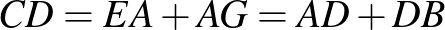 .
.
5. megoldás – forgatással
– alapötlet: szakaszok összege egy szakaszon, forgásszimmetrikus alakzat
– bizonyítás alapja: kerületi szög
– szemlélet: „kifelé” dolgozunk

Forgassuk el a 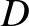 pontot az
pontot az 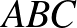 köré írt kör középpontja körül
köré írt kör középpontja körül 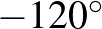 -kal, így kapjuk a
-kal, így kapjuk a 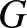 pontot.
pontot.
Az 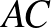 húrhoz a hosszabbik íven
húrhoz a hosszabbik íven 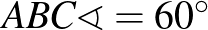 -os kerületi szög tartozik, így
-os kerületi szög tartozik, így 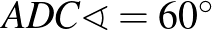 .
.
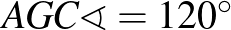 és
és 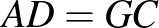 (a forgatás miatt).
(a forgatás miatt).
A 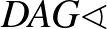 felírható három szög összegeként:
felírható három szög összegeként: 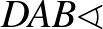 ,
, 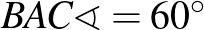 és
és 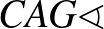 . A forgatás miatt
. A forgatás miatt 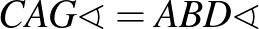 és az
és az  háromszögben
háromszögben 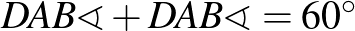 , így
, így 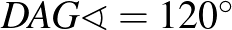 .
.
Így az 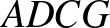 négyszög húrtrapéz, amelynek az alapokon nyugvó szögei 60, illetve 120 fokosak. Egészítsük ki ezt
négyszög húrtrapéz, amelynek az alapokon nyugvó szögei 60, illetve 120 fokosak. Egészítsük ki ezt 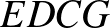 paralelogrammává. Ez megtehető úgy, hogy az
paralelogrammává. Ez megtehető úgy, hogy az 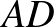 -re kifelé
-re kifelé 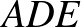 szabályos háromszöget írunk. A paralelogramma két szemközti oldalának hossza egyenlő:
szabályos háromszöget írunk. A paralelogramma két szemközti oldalának hossza egyenlő: 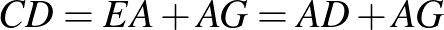 .
.
6. megoldás – koszinusztétellel (2)
– alapötlet: Koszinusztétel felírása kétszer ugyanarra az oldalra, trigonometriai összefüggések, számítások alkalmazása
– bizonyítás alapja: kerületi szög, koszinusztétel
– szemlélet: „befelé” dolgozunk
Felhasználjuk a kerületi szögekkel megkapható értékeket ( 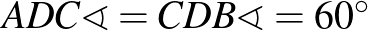 ), és felírjuk a koszinusztételt az
), és felírjuk a koszinusztételt az 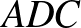 és a
és a 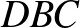 háromszögek
háromszögek 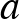 hosszú oldalaira.
hosszú oldalaira.
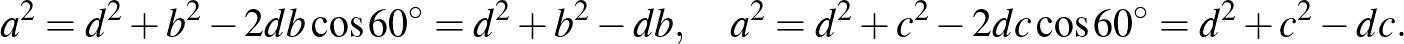
Ezek alapján 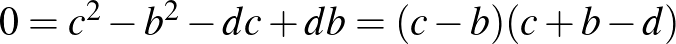 .
.
Ha 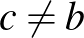 , akkor
, akkor 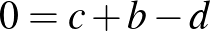 , ami éppen a keresett összefüggést jelenti,
, ami éppen a keresett összefüggést jelenti, 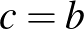 -ből pedig következik, hogy (például) az
-ből pedig következik, hogy (például) az  háromszög egy 30-60 fokos derékszögű háromszög, amelyben
háromszög egy 30-60 fokos derékszögű háromszög, amelyben 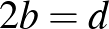 , ahonnan
, ahonnan 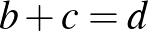 .
.
7. megoldás – területtel (3)
– alapötlet: terület felírása kétféleképpen, területek összege trigonometriai összefüggésekkel, számítások alkalmazása
– bizonyítás alapja: kerületi szög, szinuszos területképlet, koszinusztétel
– szemlélet: „befelé” dolgozunk

Az 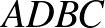 négyszög területét kétféleképpen írjuk fel. (A megoldás során felhasználjuk, hogy a kerületi szögek egyenlősége miatt
négyszög területét kétféleképpen írjuk fel. (A megoldás során felhasználjuk, hogy a kerületi szögek egyenlősége miatt 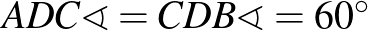 , illetve hogy
, illetve hogy  ,
, 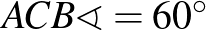 .)
.)
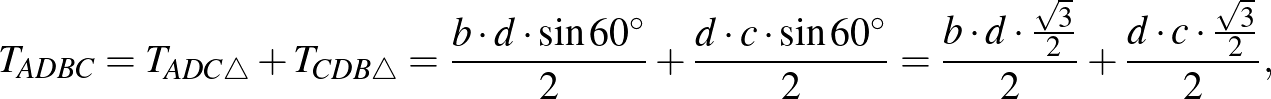
illetve
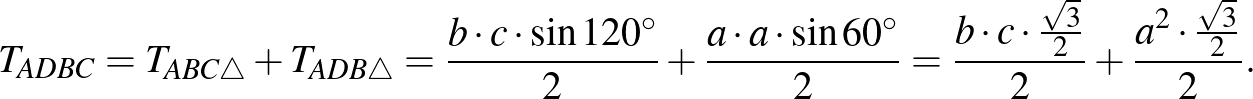
A két kifejezés egyenlő, innen 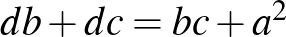 .
.
Az 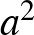 -et az
-et az 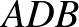 háromszögre felírt koszinusztétellel tudjuk másképp kifejezni:
háromszögre felírt koszinusztétellel tudjuk másképp kifejezni:
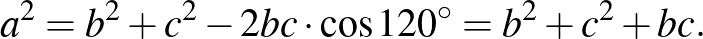
Ezt behelyettesítve a korábbi kifejezésbe: 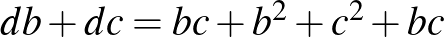 , azaz
, azaz  . Mivel
. Mivel 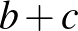 nem nulla, ebből következik, hogy
nem nulla, ebből következik, hogy 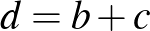 , és ezt akartuk belátni.
, és ezt akartuk belátni.
8. megoldás – szinusztétellel
– alapötlet: trigonometria, számítások alkalmazása
– bizonyítás alapja: kerületi szög, szinusztétel
– szemlélet: „befelé” dolgozunk
Felhasználjuk, hogy a 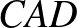 és a
és a 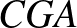 háromszögek hasonlóak (hiszen a
háromszögek hasonlóak (hiszen a  -nél lévő szögük közös,
-nél lévő szögük közös, 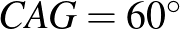 és a kerületi szögek egyenlősége miatt
és a kerületi szögek egyenlősége miatt 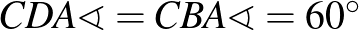 ). Ebből következik, hogy a harmadik szögük is egyenlő:
). Ebből következik, hogy a harmadik szögük is egyenlő: 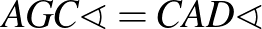 . Mivel a
. Mivel a 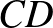 húrhoz tartozó különböző köríveken nyugvó pontok az
húrhoz tartozó különböző köríveken nyugvó pontok az 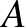 és a
és a  , így
, így 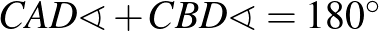 .
.
Az 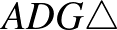 -ben
-ben 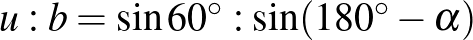 , azaz
, azaz 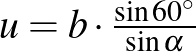 , illetve a
, illetve a 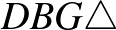 -ben
-ben 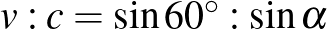 , azaz
, azaz 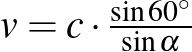 .
.
Eszerint 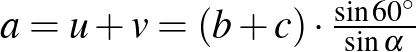 , azaz
, azaz 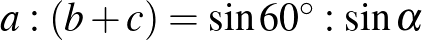 . Másrészt viszont az
. Másrészt viszont az 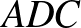 háromszögben
háromszögben 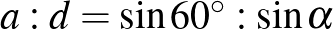 , azaz
, azaz 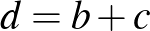 .
.
9. megoldás – Ptolemaiosz-tétellel (1)
– alapötlet: Szemléletváltás: Az ábrát a kiegészítéssel mint húrnégyszöget tekintjük, magasabb szintű geometriai alapok
– bizonyítás alapja: levezetés
– szemlélet: nem elemi geometriai megoldás, „befelé” dolgozunk.

Az 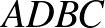 húrnégyszögben
húrnégyszögben 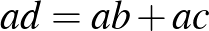 , így
, így  , ami éppen a bizonyítandó összefüggés.
, ami éppen a bizonyítandó összefüggés.
10. megoldás – koordinátageometriával
– alapötlet: Szemléletváltás, az ábrát a koordináta-rendszerbe helyezzük, koordináta-geometria
– bizonyítás alapja: koordinátageometriai összefüggések, távolság
– szemlélet: koordinatizálás (algebraizálás), nem elemi geometriai megoldás, „befelé” dolgozunk.

Legyen a kör az origó középpontú 1 sugarú kör, és legyen a háromszög három csúcsa  ,
, 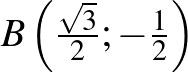 ,
,  . A
. A  pont koordinátáira fennáll, hogy
pont koordinátáira fennáll, hogy 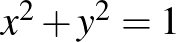 . A feladat azon feltétele, hogy
. A feladat azon feltétele, hogy  az
az  -t összekötő rövidebbik íven van azt jelenti, hogy
-t összekötő rövidebbik íven van azt jelenti, hogy 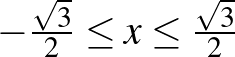 és
és 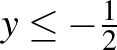 .
.
Annak érdekében, hogy elkerüljük a négyzetgyökvonást, a keresett szakaszok hosszának négyzetét számítjuk ki.
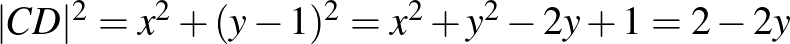 .
.
Kiszámítjuk az 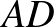 és
és 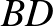 szakaszok hosszának négyzetét:
szakaszok hosszának négyzetét:
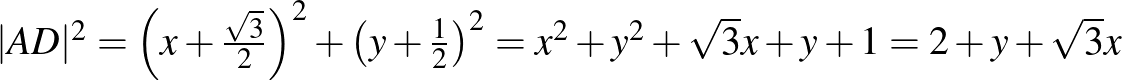 , mert
, mert 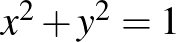 , illetve
, illetve
 .
.
Azt kellene belátni, hogy 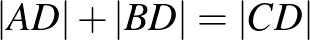 , illetve ehelyett azt, hogy
, illetve ehelyett azt, hogy 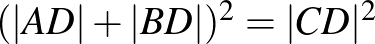 .
.
Ehhez szükség lesz a 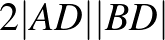 szorzatra, ezért kiszámítjuk az
szorzatra, ezért kiszámítjuk az 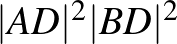 szorzatot:
szorzatot:
![$\vert AD\vert^2\vert BD\vert^2=\left[(2+y)+\sqrt3x\right]\left[(2+y)-\sqrt3x\right]
=(2+y)^2-3x^2$](/images/stories/latexuj/2021-03/2021-03-ambrusfried20210227/img137.png) . Mivel
. Mivel 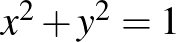 , ezt tovább alakítva
, ezt tovább alakítva 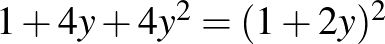 -et kapunk. Itt használjuk fel, hogy
-et kapunk. Itt használjuk fel, hogy 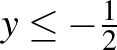 , azaz
, azaz  , ezért
, ezért 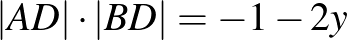 , illetve
, illetve 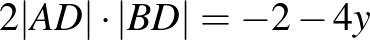 .
.
Innen 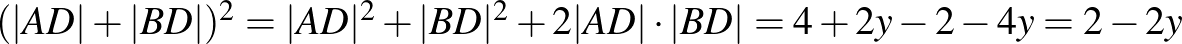 , ami valóban
, ami valóban  .
.
3. A megoldások összefüggésábrája
A problémamegoldási stratégiák explicit tanítása helyett ezek implicit módon való bemutatása sikeresebbé teszik a stratégiák alkalmazását más problémahelyzetekben is [Rott, B. & Gawlik, T. (2014).]. A stratégiák, illetve a megoldáshoz használt ismeretek összefüggésekben való konkrét tárgyalása belelendíthetik a hallgatót további megoldások keresésébe is, és ez segíti egyrészt az aktív részvételt a feladatmegoldásban, másrészt az összefüggésekben való gondolkodást az ötletkeresésnél is. A következő ábra a felhasznált matematikai eszközöket rendezte a megoldásokban történt felhasználásuk alapján.
Összefüggésábra ([Levav, A. & Leikin, R. (2010).] rendezési ötletét használva): Az ábrán feltüntettük az ismertetett megoldásokat a láncban szereplő sorszámukkal, illetve a megfigyelt hallgató (ld. [Tóth E. (2009).]) megoldásait (kékkel, dőlt betűvel), zárójelben megadva a munkájában kapott sorszámát.
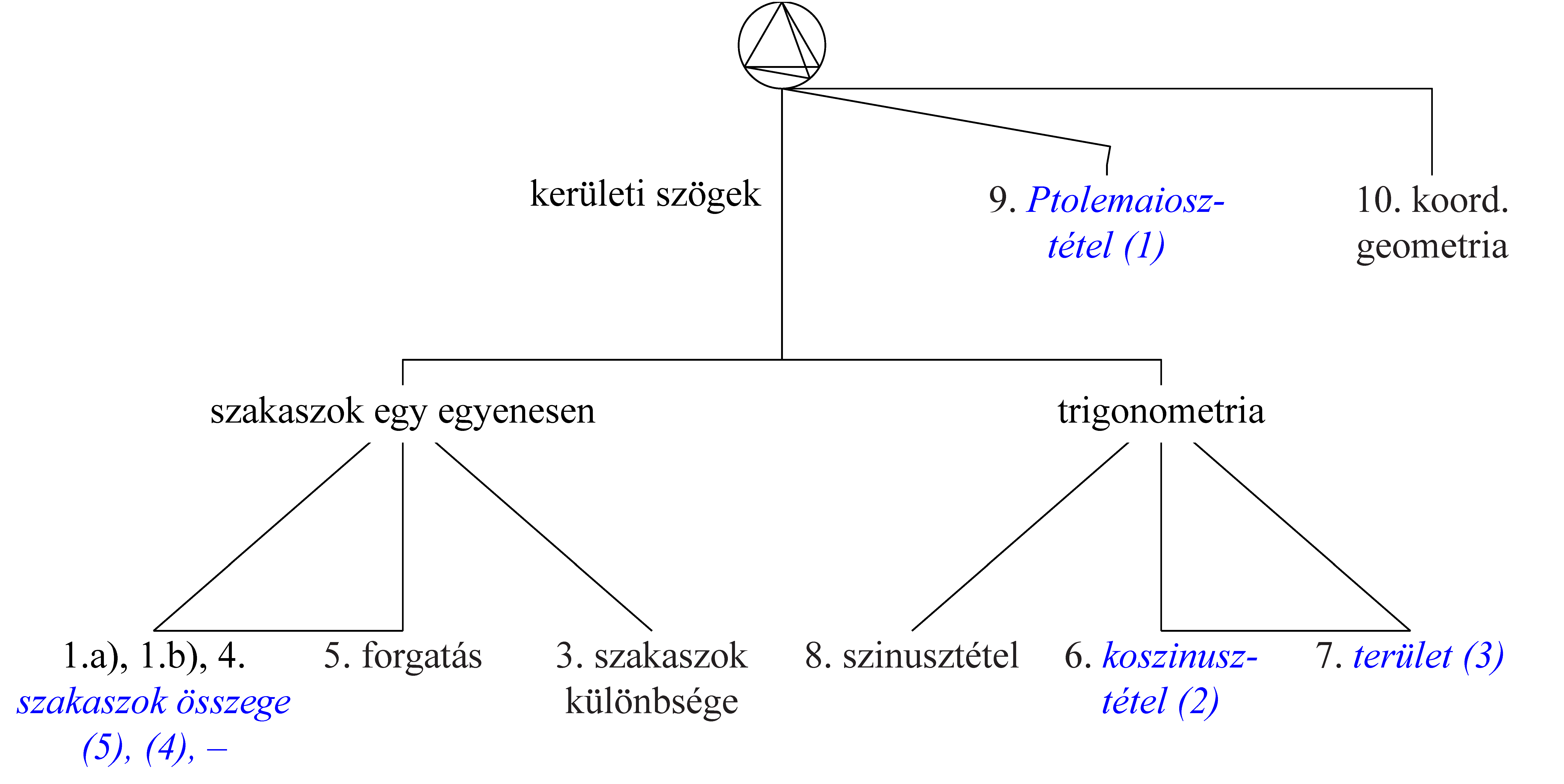
Az ábrán elrendezett 10 megoldás közül 5 szerepelt a megfigyelt hallgatónál (dőlttel kiemelve), ezek elhelyezkedése az ábrán azt is mutatja, hogy a hallgató egy-egy matematikai eszközt ötletként főleg önmagában használt, azaz nem gondolta át, hogy esetleg ezzel tovább is léphetne más megoldások készítése felé.
A megfigyelt hallgatói munkában a Ptolemaiosz-tétellel való megoldás volt az első. Ennek egyik oka lehet, hogy más (elemi) ismeretekhez képest ezt „nemrég” tanulta, illetve egy másik talán az, hogy megvolt az eszköztárában egy közvetlenül alkalmazható, megoldásra vezető tétel, és ez mindenképpen előnyt élvezett. Ez utóbbit némileg alátámasztja, hogy reflektálva megoldásaira, a hallgató ezt a megoldást tartotta a legegyszerűbbnek, és mindössze abban látta alkalmazhatóságának problémáját, hogy csak szakkörön fordulhatna elő a középiskolai oktatásban.
Érdekességképpen megjegyezzük, hogy a legbonyolultabbnak a „számítások” miatt a koszinusztételre épülő megoldást tartotta.
Több hallgatói megoldásban észrevehető volt, hogy a választott megoldáshoz sokszor használtak olyan eszközöket, amelyekkel nemrégiben találkoztak. Magasabb ismeretekre (Ptolemaiosz-tétel, koszinusztétel stb.) történő hivatkozás esetén a felhasznált tételek bizonyításának ismeretét is elvárjuk. Ilyen esetekben kiderülhet, hogy a rövidnek vélt megoldás valójában nagyon is hosszadalmas. Jellemzően szakaszok összegéhez azokat egy szakaszra másolták, ezt sokszor úgy érték el, hogy a két, egymással 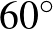 -os szöget bezáró szakasz egyikére szabályos háromszöget írtak.
-os szöget bezáró szakasz egyikére szabályos háromszöget írtak.
Megjegyezzük még, hogy a 8. és a 10. megoldás általában csak ötletként szokott felmerülni a hallgatóknál.
4. Befejező gondolatok
A tanulmányban egy, az iskolai oktatásban is használható geometriai probléma megoldásainak vizsgálatával, rendszerezésével a problémamegoldás tanításának/taníthatóságának kérdését is érintettük. Nyilván nem lehetett minden összefüggést feltárni, a hallgatók munkájának egy része a háttérben marad: nem mindent mondanak el, írnak le, így egy-egy gondolatmenet eredetére, feladatok között vont párhuzamokra nem derül mindig fény.
Továbbgondolva azt a lehetőséget,hogy a tanulókat/hallgatókat bevonjuk a megoldások készítésébe jól választott alapmegoldás(ok/ötletek) segítségével, érdemes eltűnődni azon, hogy még mire használható, ha egy (jövendő) tanár egy vagy több (nem túl nehéz) problémához kellően sok és számára rendezett megoldást ismer. Például kiválogathat belőle alkalmasan néhányat, majd ezeket tanulmányozásra adja a tanulóknak azzal a feladattal, hogy ezeket valamilyen szempont szerint rendezzék. Az ennek során végzett aktív tanulói munka komoly többletet jelent különböző megoldások „csak” olvasásával és megértésével szemben, a tanulói problémamegoldás fejlesztése szempontjából.
Tanulmányunkkal a jelenlegi iskolai oktatásban háttérbe szorult geometriai bizonyításokra is fel szeretnénk hívni a figyelmet és bízunk benne, hogy munkánk tanulságos lesz a tanár kollégák számára is.
Irodalomjegyzék
Ambrus, G. & Rott, B. (2017). Hilfestellungen beim Problemlösen in Form von „Lösungsbildern”, Mathematica Didactica. http://www.mathematica-didactica.com/altejahrgaenge/md_2017/md_2017_Ambrus_Rott_Bilder.pdf
Fried, K. (2020). Hány bőrt lehet lehúzni egy feladatról? – avagy nincs új a Nap alatt?, Érintő, 2020 június, https://ematlap.hu/tanora-szakkor-2020-11/979-hany-bort-lehet-lehuzni
Levav, A. & Leikin, R. (2010). Multiple solutions for a problem: A tool for evaluation of mathematical thinking in geometry, Proceedings of CERME 6, January 28th-February 1st 2009, Lyon France © INRP 2010 http://ife.ens-lyon.fr/publications/edition-electronique/cerme6/wg5-11-levav-leikin.pdf
Tóth E. (2009). Feladatok többféle megoldással, BSc szakdolgozat, ELTE TTK, Témavezető: Ambrus G.
Rott, B. & Gawlik, T. (2014). Explizites oder implizites Heurismentraining – was ist besser? Mathematica Didactica, (37) 191–212.
Ambrus Gabriella, Fried Katalin
ELTE TTK Matematikai Intézet, Matematikatanítási és Módszertani Központ









