Szeretem böngészni a KöMaL-archívumot, és nagyon sok kiváló feladatot találok, amelyeket tanításhoz is tudok használni.
Feltűnt, hogy egy-egy már megjelent feladat újra és újra előkerül – esetleg kicsit más köntösben.
Már a folyóirat első évtizedében többször előfordult egy nevezetes (nem feltétlenül szabályos) hatszög. Ennek a hatszögnek egyenlőek, azaz ![]() -osak a szögei, és ebből következően szemközti oldalai párhuzamosak. Egy-egy feladatban egy további adott tulajdonságából kellett egy újabbra következtetni. Ez az újabb adott és a bizonyítandó tulajdonság rendszerint ekvivalens az egyenlőszögű hatszögek körében, de attól függően, hogy melyik tulajdonság van adva, más és más irányba indíthatja el a gondolkodásunkat.
-osak a szögei, és ebből következően szemközti oldalai párhuzamosak. Egy-egy feladatban egy további adott tulajdonságából kellett egy újabbra következtetni. Ez az újabb adott és a bizonyítandó tulajdonság rendszerint ekvivalens az egyenlőszögű hatszögek körében, de attól függően, hogy melyik tulajdonság van adva, más és más irányba indíthatja el a gondolkodásunkat.
Így keletkezhettek a feladatváltozatok.
Az alábbiakban bemutatok néhány variációt a feladatra úgy, ahogyan a KöMaL-ban megjelentek, illetve hozzáfűzöm a magam változatait is. (A KöMaL kötetei nem a tanévek szerint, hanem a naptári évek szerint szerepelnek. Az oldalhivatkozások minden esetben a KöMaL nyomtatott oldalszámait jelölik.)
1903. szeptember, 26. oldal, 1195. jelű feladat. Rajzoljunk oly ![]() hatszöget, melynek szögei egyenlők s melyben
hatszöget, melynek szögei egyenlők s melyben ![]() és
és ![]() . Mutassuk meg, hogy e hatszög köré kör rajzolható. Általánosítsuk e tételt. Számítsuk ki továbbá a hatszög köré írható kör sugarát, ha
. Mutassuk meg, hogy e hatszög köré kör rajzolható. Általánosítsuk e tételt. Számítsuk ki továbbá a hatszög köré írható kör sugarát, ha ![]() és
és ![]() .
.
A megoldás az 1904. januári szám 112–113. oldalán olvasható.
(Az általánosításhoz és a számítási részhez nem fogunk hozzászólni.)
Elsőre nem nyilvánvaló, hogy a következő feladat miben hasonlít az előbbire, de hamarosan összekapcsoljuk a feladatokat.
A másik, hasonló feladat:
Matematikai olimpiász Moszkvában, verseny, 1950. év 46–47. oldal, IX.–X. csoport, 5. feladat. Bizonyítsuk be, hogy ha egy hatszög szemközti oldalai párhuzamosak és a szemközti csúcsokat összekötő átlók egyenlők, akkor kör írható a hatszög köré.
(Megoldás ugyanebben a kötetben a 153. oldalon.)
A feladat megjelent az 1958. évi Arany Dániel Matematikai Tanulóversenyen a haladók I. kategóriájában (10. évfolyam, általános tantervű osztály, 1. forduló, 3. feladat) is, amelyet a KöMaL is közölt az 1958. évi kötet 35. oldalán. Két megoldása is megjelent ugyanebben a kötetben a 45–46. oldalon.
Az óráimon a következő feladatot szoktuk tárgyalni és körüljárni:
Igazoljuk, hogy ha egy hatszög szögei egyenlők és a szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor ez húrhatszög.
Világos, hogy az egyenlőszögűségből következik a szemközti oldalak párhuzamossága, így ez a feladat az olimpiász feladatának speciális esete. Az egyenlőszögű hatszögben – mint látni fogjuk – a másodszomszédos oldalak egyenlősége és a szemközti csúcsokat összekötő átlók egyenlősége ekvivalens feltétel, azaz bármelyikből következik a másik.
Azért ebben, az olimpiász feladatánál kicsit egyszerűbb formában adom fel a tanítványaimnak a feladatot, mert éppen úgy kezdődik, mint egy másik, szintén a KöMaL hasábjain (többször is) megjelent feladat, amelyet szintén megbeszélünk.
A másik, sokkal egyszerűbb feladat a K 31., 2005. február, 96. oldal., amely szerint ha egy hatszög szögei egyenlők, akkor két szomszédos oldal összege egyenlő a velük szemközti két oldal összegével.
Ha a feladatbeli hatszög csúcsai sorban ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , akkor például
, akkor például ![]() -ből következik
-ből következik ![]() , így világos, hogy ezzel ekvivalens a következő:
, így világos, hogy ezzel ekvivalens a következő:
Gy. 2618. (1991. március, 126. oldal) és C. 1400. (2017. február, 93. oldal). Bizonyítsuk be, hogy ha egy konvex hatszög belső szögei egyenlők, akkor a hatszög bármely két szemközti oldalának különbsége ugyanakkora.
Egy lehetséges megoldás ötlete, hogy emeljünk egy-egy szabályos háromszöget két szemközti oldalra. Így egy paralelogrammává egészítettük ki a hatszöget.
Ez az ötlet még kapóra jöhet az órán tárgyalt feladat megoldáshoz is.
Megoldások és feladatvariációk az órán tárgyalt feladatra
1. megoldás. Ha a hatszög szögei egyenlők, vagyis minden szöge 120 fokos, akkor a szemközti oldalai párhuzamosak. Így például (a szokásos jelöléseket használva) az ![]() négyszög trapéz, mert
négyszög trapéz, mert ![]() , és mivel két átlója,
, és mivel két átlója, ![]() és
és ![]() ugyanolyan hosszú, így húrtrapéz is;
ugyanolyan hosszú, így húrtrapéz is; ![]() és
és ![]() szakaszfelező merőlegese a szimmetriatengely.
szakaszfelező merőlegese a szimmetriatengely.
Az ![]() oldallal
oldallal ![]() -ben
-ben ![]() -os és a
-os és a ![]() oldallal
oldallal ![]() -ben
-ben ![]() -os szöget bezáró félegyenesek metszéspontja
-os szöget bezáró félegyenesek metszéspontja ![]() , illetve az
, illetve az ![]() oldallal
oldallal ![]() -ban
-ban ![]() -os és a
-os és a ![]() oldallal
oldallal ![]() -ben
-ben ![]() -os szöget bezáró félegyenesek metszéspontja
-os szöget bezáró félegyenesek metszéspontja ![]() . Mivel az említettek az
. Mivel az említettek az ![]() szimmetriatengelyére szimmetrikusan elhelyezkedő félegyenesek, a metszéspontjaik is szimmetrikusan helyezkednek el. Ezek szerint a hatszögnek van egy szimmetriatengelye.
szimmetriatengelyére szimmetrikusan elhelyezkedő félegyenesek, a metszéspontjaik is szimmetrikusan helyezkednek el. Ezek szerint a hatszögnek van egy szimmetriatengelye.
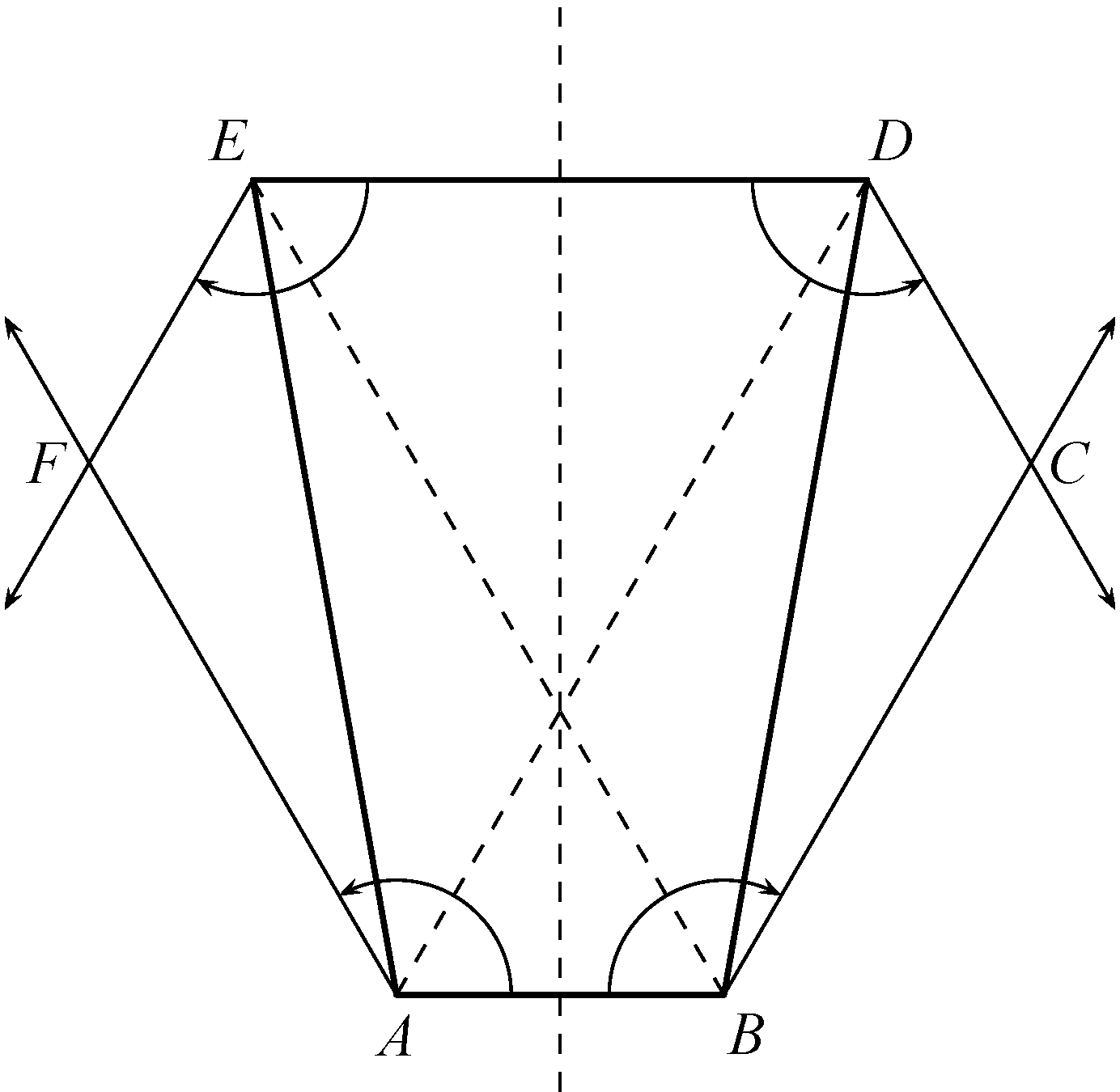
Ugyanígy kiválaszthattuk volna a ![]() vagy a
vagy a ![]() négyszöget is, ezért a hatszögnek három szimmetriatengelye is van.
négyszöget is, ezért a hatszögnek három szimmetriatengelye is van.
A befejezésre két lehetőséget mutatunk.
1. lehetőség. Az ![]() -t merőlegesen felező
-t merőlegesen felező ![]() és a
és a ![]() -t merőlegesen felező
-t merőlegesen felező ![]() szimmetriatengek
szimmetriatengek ![]() metszéspontjára a
metszéspontjára a ![]() ,
, ![]() tengelyes szimmetriák miatt fennáll:
tengelyes szimmetriák miatt fennáll: 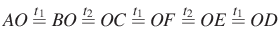 . Eszerint mind a hat csúcs ugyanolyan távol van
. Eszerint mind a hat csúcs ugyanolyan távol van ![]() -tól, a hatszög köré kör írható, amelynek középpontja
-tól, a hatszög köré kör írható, amelynek középpontja ![]() . Az is látszik ebből a megoldásból, hogy
. Az is látszik ebből a megoldásból, hogy ![]() , mert az
, mert az ![]() húrhoz tartozó középponti szög, sőt,
húrhoz tartozó középponti szög, sőt, ![]() is ennyi, valamint
is ennyi, valamint ![]() , ezért a hatszög ráadásul 120 fokos forgásszimmetriával is rendelkezik.
, ezért a hatszög ráadásul 120 fokos forgásszimmetriával is rendelkezik.
2. lehetőség. Belátható, hogy egy olyan hatszög, amelynek három (oldalközépponton átmenő) szimmetriatengelye van, ![]() -os forgásszimmetriával rendelkezik. (Először is tudni kell, hogy két metsző tengelyű tükrözés egymásutánja forgatást eredményez, amelynek szöge a tengelyek által bezárt szög kétszerese. Másodszor be kell látni, hogy a tengelyek csakis egy pontban metszhetik egymást – ellenkező esetben lenne olyan pontja a hatszögnek, amelyet elég sokszor tükrözve a tengelyekre, a kép a hatszögön kívül kerülne. Eszerint
-os forgásszimmetriával rendelkezik. (Először is tudni kell, hogy két metsző tengelyű tükrözés egymásutánja forgatást eredményez, amelynek szöge a tengelyek által bezárt szög kétszerese. Másodszor be kell látni, hogy a tengelyek csakis egy pontban metszhetik egymást – ellenkező esetben lenne olyan pontja a hatszögnek, amelyet elég sokszor tükrözve a tengelyekre, a kép a hatszögön kívül kerülne. Eszerint ![]() -t
-t ![]() -kal elforgatva
-kal elforgatva ![]() -t kapjuk,
-t kapjuk, ![]() -t
-t ![]() -kal elforgatva – ugyanazon középpont körül –
-kal elforgatva – ugyanazon középpont körül – ![]() -t,
-t, ![]() -t
-t ![]() -kal elforgatva
-kal elforgatva ![]() -t. Hasonlóan,
-t. Hasonlóan, ![]() -ből
-ből ![]() -t,
-t, ![]() -ből
-ből ![]() -et kapjuk.)
-et kapjuk.)
A 120 fokos forgásszimmetriából következik, hogy a másodszomszédos csúcsok szabályos háromszöget határoznak meg, és mivel a hatszög szögei 120 fokosak, azért – például – ![]() háromszög szabályos és
háromszög szabályos és ![]() húrnégyszög, aminek körülírt körére – a forgásszimmetria miatt – illeszkedik
húrnégyszög, aminek körülírt körére – a forgásszimmetria miatt – illeszkedik ![]() és
és ![]() is.
is.
Következésképp a hatszög húrhatszög.
Ebből a megoldásból máris kapunk néhány újabb feladatvariációt:
1. variáció az eredeti feladatra. Bizonyítsuk be, hogy ha egy hatszög szögei egyenlők és szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor forgásszimmetrikus. (KöMaL C. 1570, 2019. november, 483. oldal)
Megfordítva, vagyis abból, hogy egy egyenlőszögű hatszög forgásszimmetrikus, nem következik, hogy a szemközti csúcsait összekötő átlók egyenlő hosszúak. (Hiszen lehet, hogy a forgásszimmetria szöge ![]() .) A 120 fokos forgásszimmetriából viszont már igen.
.) A 120 fokos forgásszimmetriából viszont már igen.
2. variáció az eredeti feladatra. Bizonyítsuk be, hogy ha egy hatszög szögei egyenlők és szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor a hatszög másodszomszédos oldalai egyenlő hosszúak.
Ez megfordítva is igaz: abból, hogy az egyenlőszögű hatszög másodszomszédos oldalai egyenlő hosszúak, következik, hogy a szemközti csúcsait összekötő átlói egyenlő hosszúak. Sőt, a forgásszimmetria is következik.
Megjegyzés. Vegyük észre, hogy a 2. variációban bizonyítandó tulajdonság a korábban említett, 1195. jelű feladat feltétele.
3. variáció az eredeti feladatra. Bizonyítsuk be, hogy ha egy hatszög szögei egyenlők és szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor a hatszög másodszomszédos csúcsai szabályos háromszöget határoznak meg.
Ennek a megfordítottja (ha az egyenlőszögű hatszög másodszomszédos csúcsai szabályos háromszöget alkotnak, akkor a szemközti csúcsait összekötő átlók egyenlő hosszúak) is igaz.
Kiválasztva ugyanis az ![]() ,
, ![]() ,
, ![]() csúcsokat, a szögegyenlőség miatt a
csúcsokat, a szögegyenlőség miatt a ![]() csúcs az
csúcs az ![]() köré írható kör rövidebbik
köré írható kör rövidebbik ![]() ívén van (látószög), és ugyanígy a rövidebbik
ívén van (látószög), és ugyanígy a rövidebbik ![]() íven van
íven van ![]() , illetve a rövidebbik
, illetve a rövidebbik ![]() íven van
íven van ![]() . Ezért a hatszög húrhatszög, és mivel
. Ezért a hatszög húrhatszög, és mivel ![]() és
és ![]() szabályos háromszögek, így forgatással egymásba vihetők, ezért a szemközti csúcsokat összekötő átlók egyenlő hosszúak. (Például az
szabályos háromszögek, így forgatással egymásba vihetők, ezért a szemközti csúcsokat összekötő átlók egyenlő hosszúak. (Például az ![]() -t elforgatva a megfelelő szöggel
-t elforgatva a megfelelő szöggel ![]() -t, illetve
-t, illetve ![]() -et kapjuk.)
-et kapjuk.)
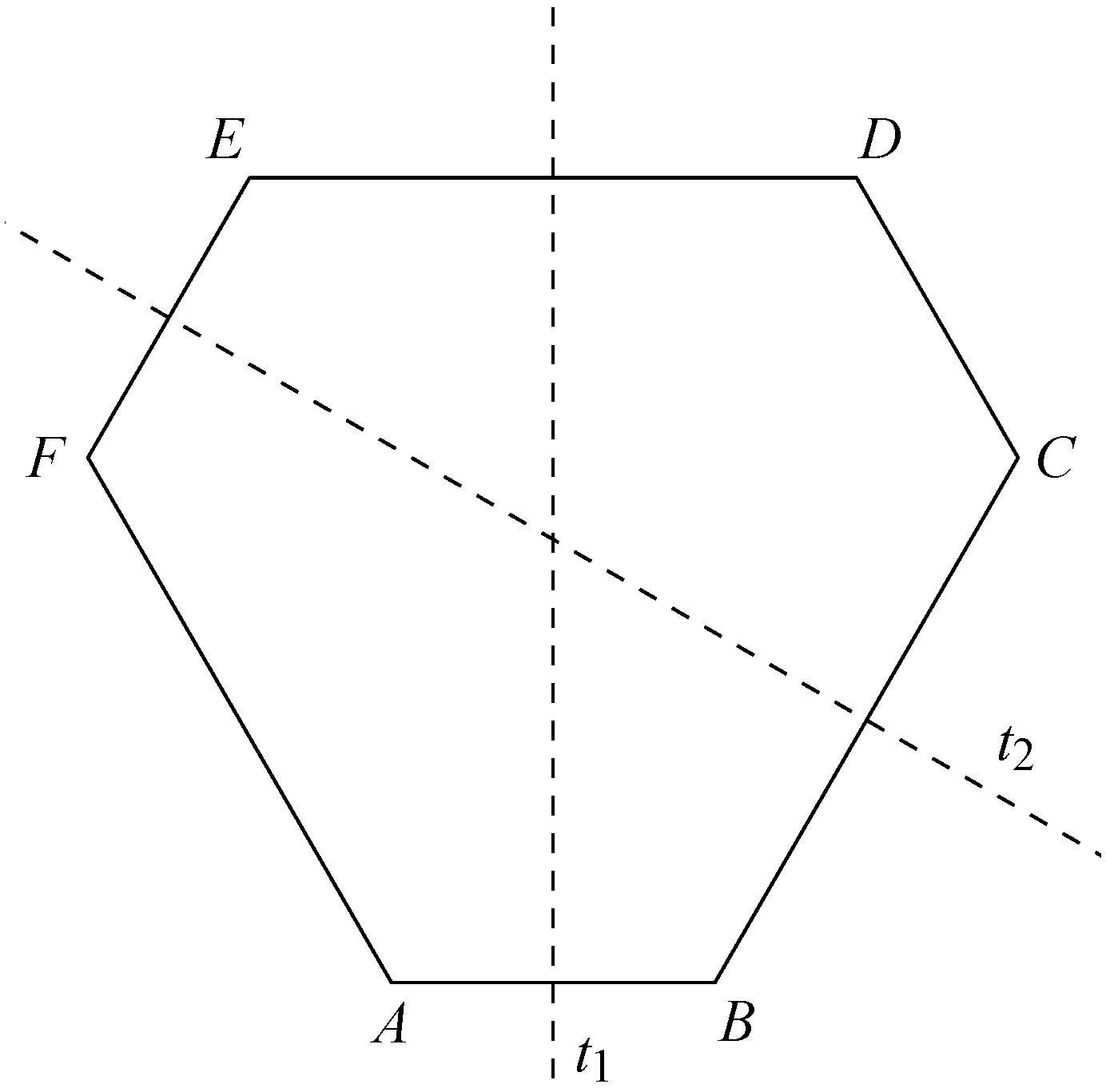
2. megoldás. Húzzuk be minden második oldal egyenesét. Legyen például ![]() és
és ![]() egyenesének metszéspontja
egyenesének metszéspontja ![]() ,
, ![]() és
és ![]() egyenesének metszéspontja
egyenesének metszéspontja ![]() ,
, ![]() és
és ![]() egyenesének metszéspontja
egyenesének metszéspontja ![]() . A hatszög minden külső szöge
. A hatszög minden külső szöge ![]() , és ha egy háromszög két szöge
, és ha egy háromszög két szöge ![]() -os, akkor az szabályos, ezért a három egyenes által közrezárt háromszög, azaz
-os, akkor az szabályos, ezért a három egyenes által közrezárt háromszög, azaz ![]() is szabályos.
is szabályos.
A hatszög szomszédos oldalai ![]() -os szöget zárnak be egymással, így (például)
-os szöget zárnak be egymással, így (például) ![]() . Ebből következik, hogy
. Ebből következik, hogy ![]() . Hasonlóan látható, hogy
. Hasonlóan látható, hogy ![]() ,
, ![]() .
.
Mivel pedig ![]() , következésképp
, következésképp ![]() , mert
, mert ![]() és
és ![]() szimmetrikusan helyezkedik el az
szimmetrikusan helyezkedik el az ![]() (azaz
(azaz ![]() ) szakaszfelező merőlegesére.
) szakaszfelező merőlegesére.
Így nemcsak ![]() és
és ![]() , hanem
, hanem ![]() , sőt,
, sőt, ![]() is ezekkel egyenlő hosszú.
is ezekkel egyenlő hosszú.
A hatszög tehát úgy kapható, hogy egy szabályos háromszög minden csúcsából ugyanakkora oldalhosszúságú szabályos háromszögeket vágunk le. Eszerint a hatszög csúcsai egyenlő távolságra vannak az ![]() szabályos háromszög középpontjától, a hatszög húrhatszög.
szabályos háromszög középpontjától, a hatszög húrhatszög.
4. variáció az eredeti feladatra. Bizonyítsuk be, hogy ha egy hatszög szögei egyenlők és szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor a hatszög másodszomszédos oldalainak egyenese olyan szabályos háromszöget zár közre, amelynek csúcsaitól egyenlő távolságra vannak a hozzájuk legközelebb eső hatszögcsúcsok.
Vegyük észre, hogy az 1903-ban kitűzött 1195. jelű feladatban a hatszög körbe írhatóságát nem a szemközti csúcsokat összekötő átlók, hanem a másodszomszédos oldalak egyenlőségéből kell bizonyítani.
Igazolható, hogy egy egyenlő szögű hatszögben akkor és csak akkor egyenlő a szemközti csúcsokat összekötő átlók hossza, ha a hatszög másodszomszédos oldalai egyenlő hosszúak.
Az egyik irány (ha egyenlő hosszúak az átlók, akkor egyenlő hosszúak a másodszomszédos oldalak) például a fenti bizonyításból következik. A másik irány (ha egyenlő hosszúak a másodszomszédos oldalak, akkor egyenlő hosszúak az átlók) például így igazolható: Írjunk szabályos háromszögeket a másodszomszédos oldalakra kifelé: ![]() ,
, ![]() ,
, ![]() . Ezzel egy
. Ezzel egy ![]() szabályos háromszöget kapunk. Mivel
szabályos háromszöget kapunk. Mivel ![]() , ebből (például a forgásszimmetriára való tekintettel) következik, hogy
, ebből (például a forgásszimmetriára való tekintettel) következik, hogy ![]() , azaz a szemközti csúcsokat összekötő átlók egyenlő hosszúak.
, azaz a szemközti csúcsokat összekötő átlók egyenlő hosszúak.
3. megoldás. Az 1. megoldásból láttuk, hogy (például) ![]() és
és ![]() , illetve
, illetve ![]() egymással szimmetrikusan helyezkedik el az
egymással szimmetrikusan helyezkedik el az ![]() szimmetrikus trapéz tengelyére. Ebből következik, hogy
szimmetrikus trapéz tengelyére. Ebből következik, hogy ![]() merőleges a szimmetriatengelyre, vagyis párhuzamos
merőleges a szimmetriatengelyre, vagyis párhuzamos ![]() -vel és
-vel és ![]() -vel is. Mivel a
-vel is. Mivel a ![]() négyszögben
négyszögben ![]() -nél és
-nél és ![]() -nél ugyanakkora (
-nél ugyanakkora (![]() -os) szögek vannak, ebből következik, hogy
-os) szögek vannak, ebből következik, hogy ![]() húrtrapéz. Hasonlóan nyilván
húrtrapéz. Hasonlóan nyilván ![]() is húrtrapéz.
is húrtrapéz.
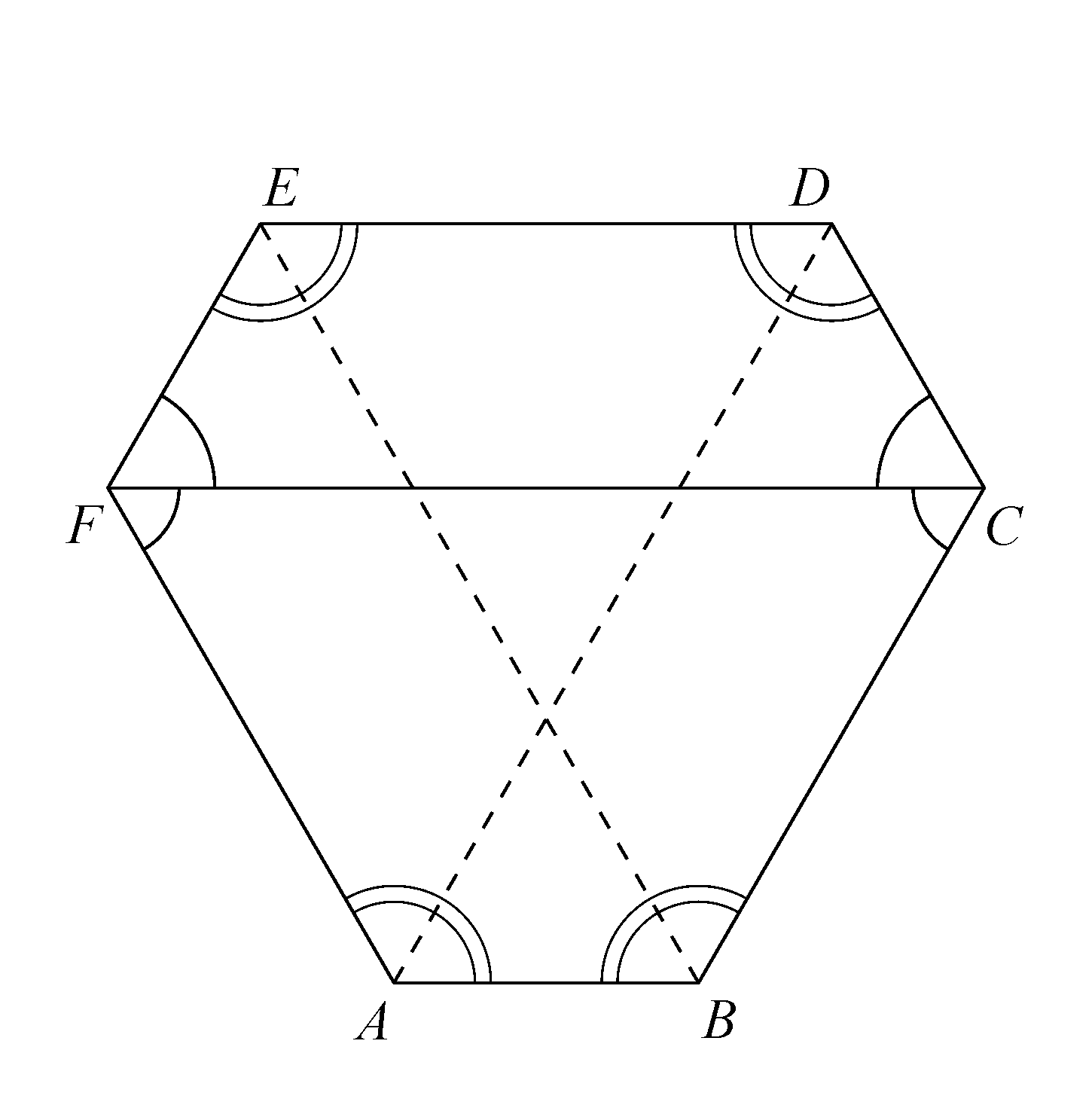
Ezt a gondolatmenetet bármelyik szemközti oldalpárra levezethetjük.
Eszerint az ![]() ,
, ![]() ,
, ![]() pontok köré írható körre illeszkedik
pontok köré írható körre illeszkedik ![]() is (mert
is (mert ![]() húrtrapéz),
húrtrapéz), ![]() is (mert
is (mert ![]() húrtrapéz) és
húrtrapéz) és ![]() is (mert
is (mert ![]() húrtrapéz).
húrtrapéz).
Ebből következik, hogy a hatszög húrhatszög.
5. variáció az eredeti feladatra. Bizonyítsuk be, hogy ha egy hatszög szögei egyenlők és szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor a szóbanforgó átlók párhuzamosak egy-egy hatszögoldallal.
Ennek a variációnak a megfordítása is igaz: Ha az egyenlőszögű hatszög szemközti csúcsait összekötő átlói párhuzamosak egy-egy megfelelő hatszögoldallal, akkor ezek az átlók egyenlő hosszúak.
Na, még egy variáció!
Ezúttal egy másik feladat felől közelítjük meg az eredetit:
Igazoljuk, hogy ha egy ![]() szabályos háromszög köré írható körén a rövidebbik
szabályos háromszög köré írható körén a rövidebbik ![]() íven felveszünk egy
íven felveszünk egy ![]() pontot, akkor
pontot, akkor ![]() !
!
Erre is több (szám szerint két) megoldást adunk.
1. megoldás. Mivel ![]() húrnégyszög,
húrnégyszög, ![]() . Az
. Az ![]() húrhoz tartozó
húrhoz tartozó ![]() és
és ![]() szögek egyenlők, azaz
szögek egyenlők, azaz ![]() . Ezért
. Ezért ![]() is 60 fokos.
is 60 fokos.
Rajzoljunk ![]() -re
-re ![]() szabályos háromszöget úgy, hogy
szabályos háromszöget úgy, hogy ![]() a körön kívülre essen. Mivel
a körön kívülre essen. Mivel ![]() és
és ![]() is 60 fokos szöget zár be
is 60 fokos szöget zár be ![]() egyensével, azért
egyensével, azért ![]() .
.
Jelölje az ![]() egyenesének és a körnek a másik metszéspontját
egyenesének és a körnek a másik metszéspontját ![]() (az egyik maga az
(az egyik maga az ![]() pont).
pont).
A ![]() húrnégyszög, ezért
húrnégyszög, ezért ![]() .
.
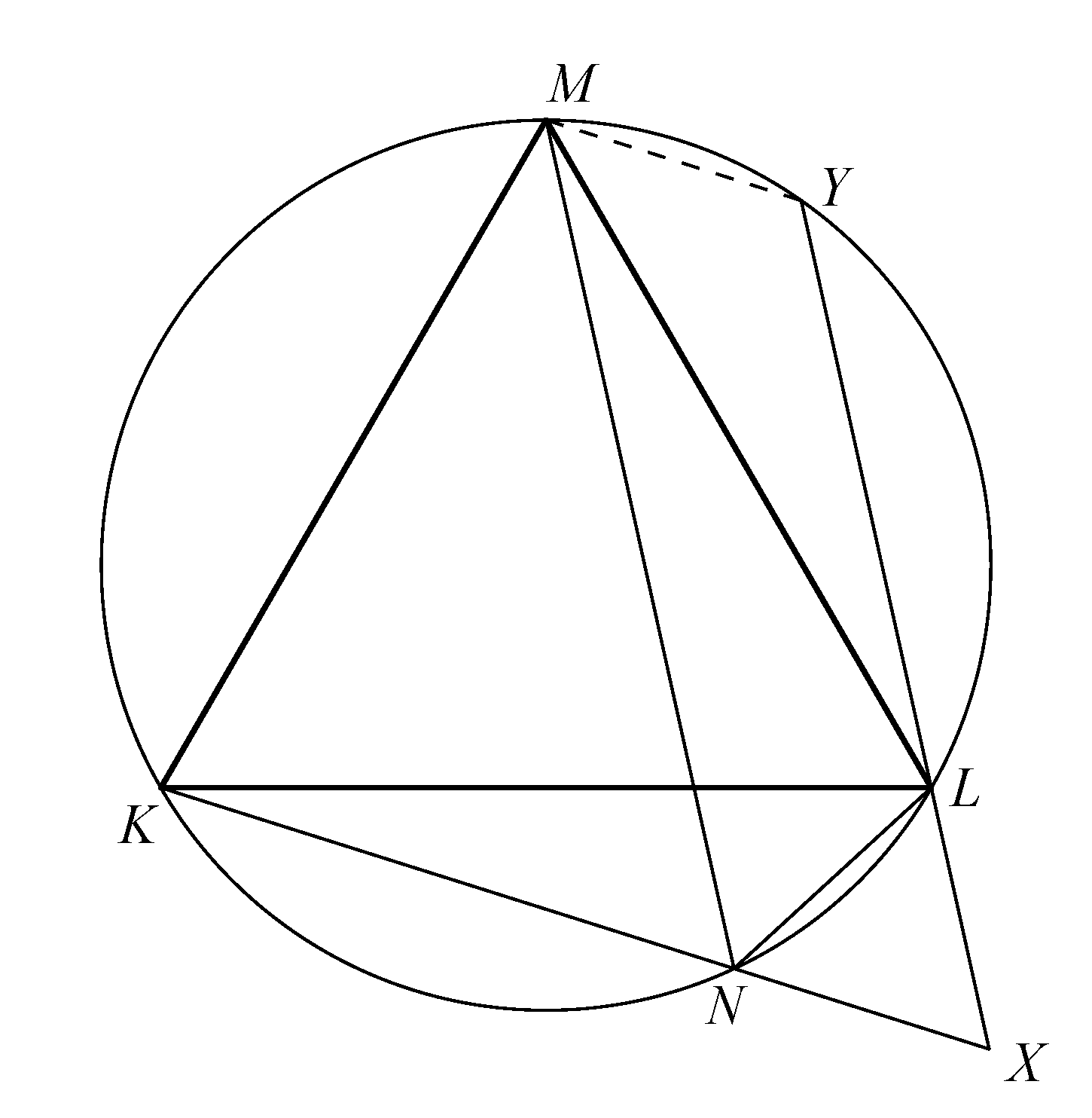
Mivel az ![]() négyszögnek két szemközti szöge,
négyszögnek két szemközti szöge, ![]() egyenlő, valamint
egyenlő, valamint ![]() , így
, így ![]() paralelogramma.
paralelogramma.
![]() és
és ![]() háromszögek egybevágók, mert két oldaluk ugyanolyan hosszú (
háromszögek egybevágók, mert két oldaluk ugyanolyan hosszú (![]() és
és ![]() ), továbbá a hosszabbik oldallal szemközti szögük egyenlő (
), továbbá a hosszabbik oldallal szemközti szögük egyenlő ( ![]() ).
).
Ebből következik, hogy ![]() , de az
, de az ![]() paralelogrammából, illetve
paralelogrammából, illetve ![]() szabályos háromszögből ekkor
szabályos háromszögből ekkor ![]() következik, ami éppen a feladat állítása.
következik, ami éppen a feladat állítása.
2. megoldás. „Ágyúval lövünk verébre”, és alkalmazzuk a Ptolemaiosz-tételt, miszerint egy húrnégyszögben a szemközti oldalak szorzatának összege egyenlő az átlók szorzatával, esetünkben:
amelyet elosztva a háromszög oldalhosszával (![]() ) adódik a bizonyítandó összefüggés.
) adódik a bizonyítandó összefüggés.
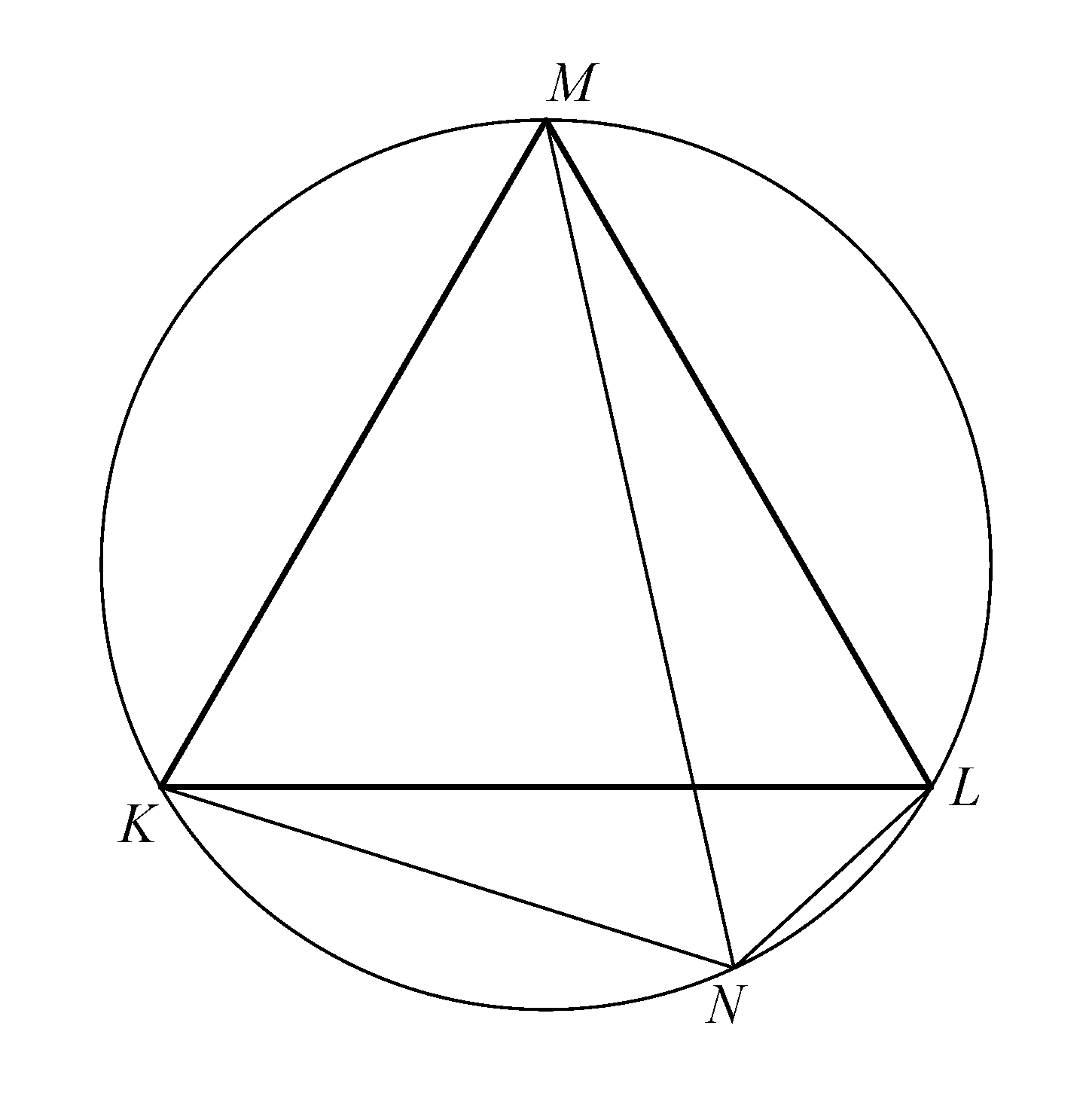
(Persze, ilyenkor fel szoktam adni a Ptolemaiosz-tétel bizonyítását házi feladatnak.)
Térjünk most vissza az eredeti feladathoz.
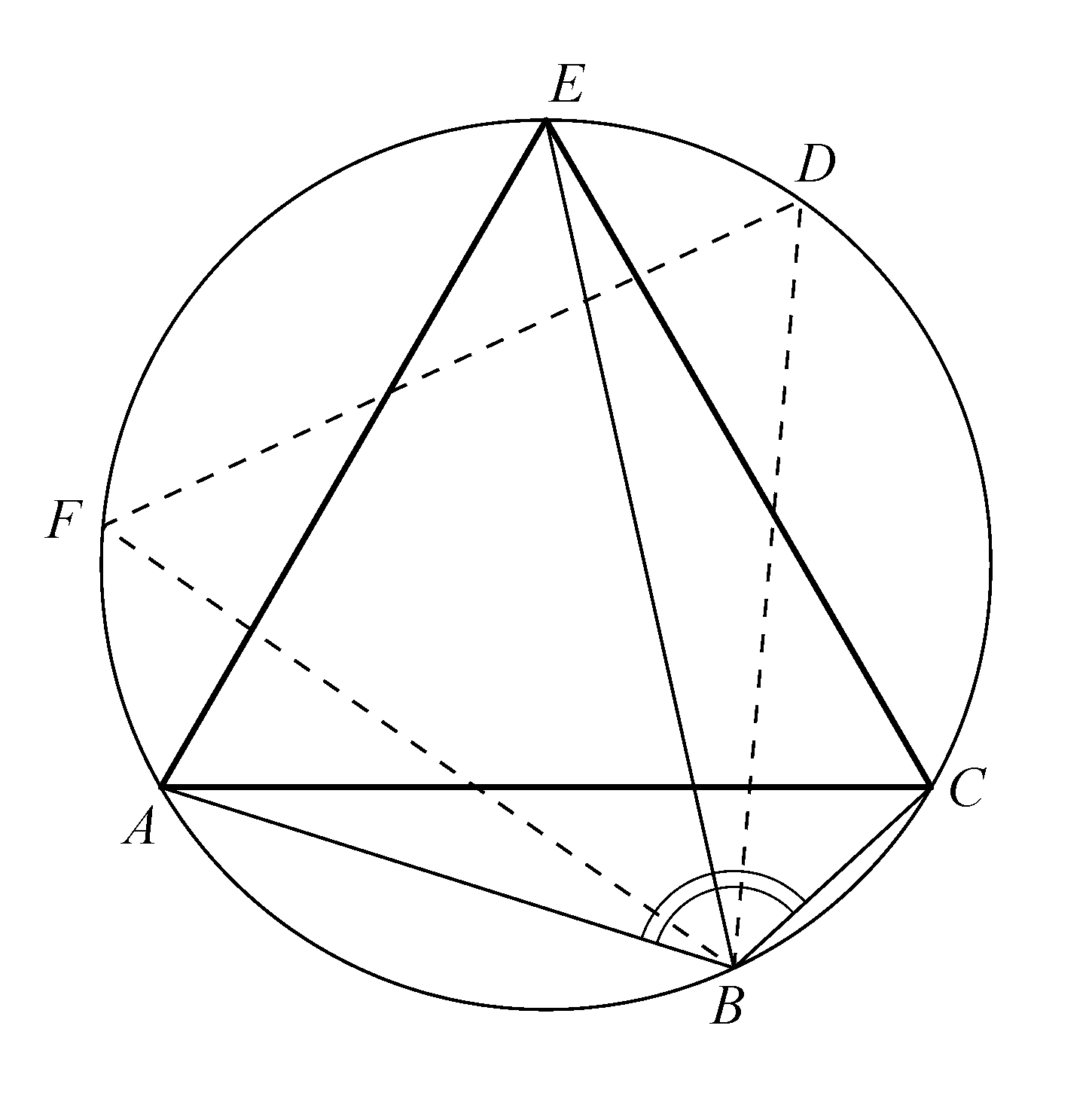
Korábban, az első megoldásban bebizonyítottuk, hogy ha egy hatszög szögei egyenlők és a szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor a másodszomszédos csúcsai szabályos háromszöget határoznak meg. Például az ![]() hatszögben
hatszögben ![]() szabályos háromszög, minden szöge
szabályos háromszög, minden szöge ![]() -os. Mivel
-os. Mivel ![]() , így
, így ![]() is illeszkedik az
is illeszkedik az ![]() köré írható körre.
köré írható körre.
Ezért az előzőekben tárgyalt feladat értelmében fennáll rá, hogy ![]() .
.
Ez elvezet minket egy újabb feladatvariációhoz:
6. variáció az eredeti feladatra. Bizonyítsuk be, hogy ha egy hatszög szögei egyenlők és szemközti csúcsait összekötő átlói egyenlő hosszúak, akkor a szóbanforgó átló hossza egyenlő két szomszédos oldal hosszának összegével.
Ennek a variációnak a megfordítása is igaz: Ha az egyenlőszögű hatszög szemközti csúcsait összekötő átlói hossza egyenlő két szomszédos oldal hosszának összegével (persze meg kell mondanunk, hogy melyik két szomszédos oldal, ezzel legalább két feladatot kapunk), akkor ezek az átlók egyenlő hosszúak.
Az általánosabb feladat egy megoldása
Következzék végül a moszkvai olimpiász 3. feladatának egy, a KöMaL-ban nem közölt, további megoldása:
Megmutatjuk, hogy az ![]() ,
, ![]() ,
, ![]() pontok meghatározzák a többit, és azok illeszkednek az
pontok meghatározzák a többit, és azok illeszkednek az ![]() háromszög köré írt körre.
háromszög köré írt körre.
Korábban beláttuk, ha az ![]() hatszög szemközti oldalai párhuzamosak és a szemközti csúcsokat összekötő átlói egyenlő hosszúak, akkor
hatszög szemközti oldalai párhuzamosak és a szemközti csúcsokat összekötő átlói egyenlő hosszúak, akkor ![]() ,
, ![]() és
és ![]() mindegyike trapéz.
mindegyike trapéz.
Jelölje ![]() és
és ![]() közös szakaszfelező merőlegesét
közös szakaszfelező merőlegesét ![]() ,
, ![]() és
és ![]() közös szakaszfelező merőlegesét
közös szakaszfelező merőlegesét ![]() ,
, ![]() és
és ![]() közös szakaszfelező merőlegesét
közös szakaszfelező merőlegesét ![]() . Ezek a tengelyek nem lehetnek párhuzamosak, mert a hatszög szomszédos oldalpárjainak szakaszfelező merőlegesei.
. Ezek a tengelyek nem lehetnek párhuzamosak, mert a hatszög szomszédos oldalpárjainak szakaszfelező merőlegesei.
![]() -t tükrözve
-t tükrözve ![]() -re
-re ![]() -t kapjuk,
-t kapjuk, ![]() -t
-t ![]() -re
-re ![]() -t,
-t, ![]() -t
-t ![]() -ra
-ra ![]() -t,
-t, ![]() -t
-t ![]() -re
-re ![]() -t,
-t, ![]() -t
-t ![]() -re
-re ![]() -et, végül
-et, végül ![]() -et
-et ![]() -ra
-ra ![]() -t.
-t.
Vagyis ![]() fixpontja a
fixpontja a ![]() tükrözéskompozíciónak.
tükrözéskompozíciónak.
Ha ![]() ,
, ![]() és
és ![]() nem egy pontban metszi egymást, akkor
nem egy pontban metszi egymást, akkor ![]() kompozíció egy (olyan) csúsztatva tükrözés lenne, amelynek nincs fixpontja. A
kompozíció egy (olyan) csúsztatva tükrözés lenne, amelynek nincs fixpontja. A ![]() kompozíció eltolás, ennek sincs fixpontja. Ezért szükséges, hogy a három tükörtengely egy pontban messe egymást.
kompozíció eltolás, ennek sincs fixpontja. Ezért szükséges, hogy a három tükörtengely egy pontban messe egymást.
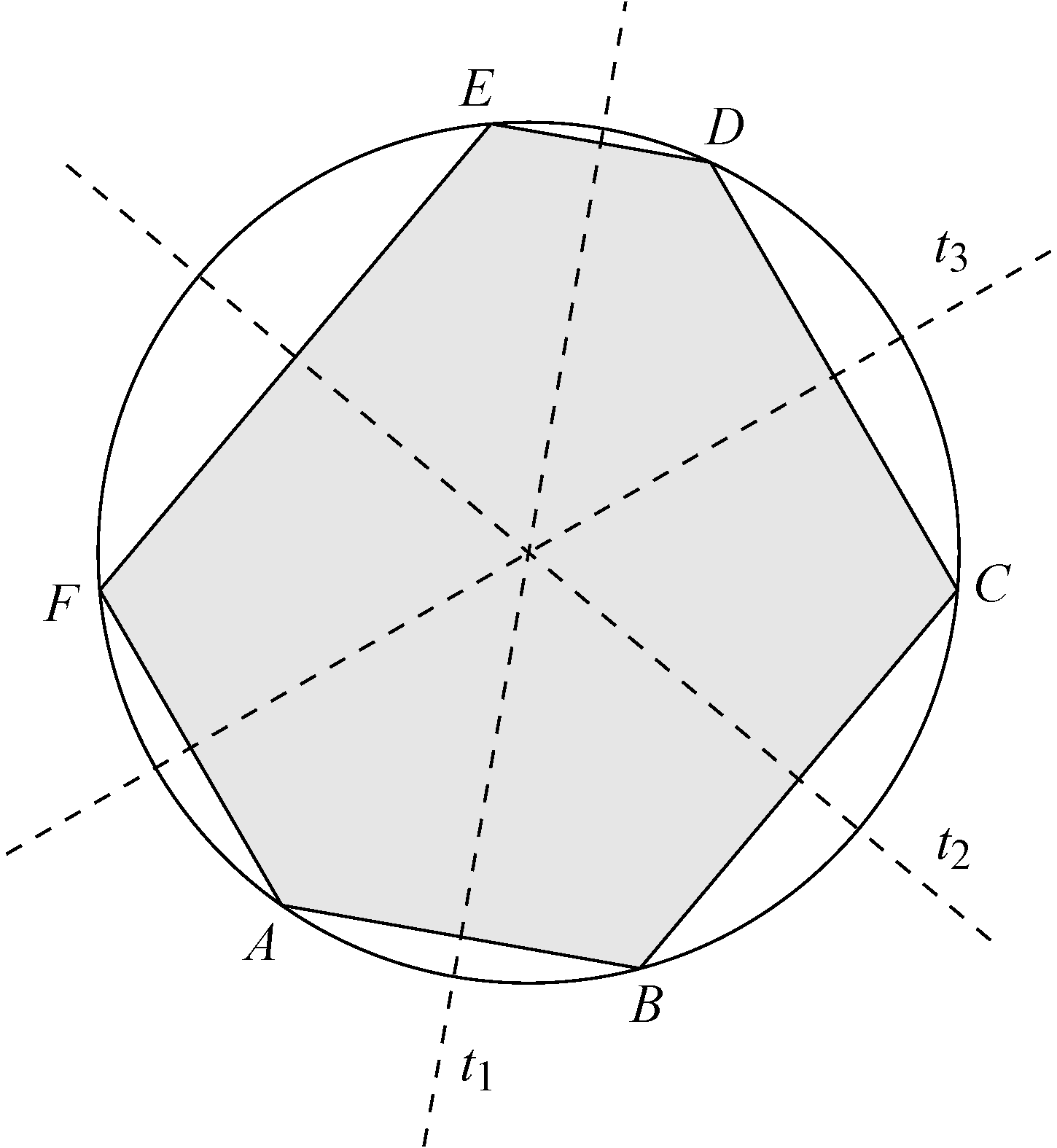
Ha viszont a három tengely egy pontban metszi egymás, akkor mivel ![]() és
és ![]() az
az ![]() ,
, ![]() ,
, ![]() köré írható kör középpontjában metszi egymást, szükségszerűen
köré írható kör középpontjában metszi egymást, szükségszerűen ![]() szakaszfelező merőlegese is átmegy a kör középpontján, tehát
szakaszfelező merőlegese is átmegy a kör középpontján, tehát ![]() illeszkedik a körre (mivel
illeszkedik a körre (mivel ![]() illeszkedik).
illeszkedik).
Ebből következik, hogy a hatszög húrhatszög.
Az is látható azonban, hogy az nem szükségszerű, hogy a másodszomszédos oldalak egyenlő hosszúak legyenek, vagy hogy a hatszög minden szöge ugyanakkora legyen.
Hasonló feladatok
Nos, a feladatvariációk tárháza, úgy tűnik, kimeríthetetlen. Miközben ezt a cikket írtam, áttekintettem a KöMaL archívumát, és rengeteg, a fentiekhez hasonló feladatot véltem felfedezni.
Az érdekesség kedvéért kigyűjtöttem néhányat.
CCXCVII. (1934. évfolyam, 212. oldal): Adva van az (![]() ) egyenlőszögű hatszög úgy, hogy
) egyenlőszögű hatszög úgy, hogy ![]() és
és ![]() . Legyen e hatszög egy szabályos oktaéder síkmetszete. Szerkesszük meg hozzá az oktaédert!
. Legyen e hatszög egy szabályos oktaéder síkmetszete. Szerkesszük meg hozzá az oktaédert!
1193. feladat és megoldása (1936. évfolyam, 212–213. oldal): A háromszög magasságainak talppontjából merőlegeseket állítunk a háromszög oldalaira. Bizonyítsuk be, hogy ezek talppontjai (szám szerint 6) egy körön feküsznek.
A feladat megoldásához (lásd ott) fűzött megjegyzés: A feladatban tárgyalt kör az úgynevezett Taylor-féle kör. Kimutatható, hogy az ![]() hatszög
hatszög ![]() ,
, ![]() ,
, ![]() átlói egyenlők. Ebből következik, hogy csúcsai egy körön fekszenek.
átlói egyenlők. Ebből következik, hogy csúcsai egy körön fekszenek.
Gy. 2867. (1993. évfolyam, 317. oldal) A körbe írt ![]() hatszögben
hatszögben ![]() ,
, ![]() ,
, ![]() és a hatszög területe kétszerese az
és a hatszög területe kétszerese az ![]() háromszög területének. Mutassuk meg, hogy a hatszög párhuzamos oldalai egyenlő hosszúak.
háromszög területének. Mutassuk meg, hogy a hatszög párhuzamos oldalai egyenlő hosszúak.
Az 1958. évi Kürschák József matematikai tanulóverseny 3. feladata (1959. évi kötet 70–77. oldal): Az ![]() konvex hatszögben az
konvex hatszögben az ![]() és
és ![]() , a
, a ![]() és
és ![]() , továbbá a
, továbbá a ![]() és
és ![]() oldalak párhuzamosak. bizonyítsuk be, hogy az
oldalak párhuzamosak. bizonyítsuk be, hogy az ![]() és
és ![]() háromszögek területe egyenlő.
háromszögek területe egyenlő.
Gy. 2570., 1989. szeptember, 270. oldal Egy hatszög minden szöge ![]() , oldalai felváltva 1 és
, oldalai felváltva 1 és ![]() cm hosszúak. Mekkora a hatszög területe?
cm hosszúak. Mekkora a hatszög területe?
Hálával tartozom a diákjaimnak, akik lelkesen megoldják a kitűzött feladatot, és újabb és újabb ötletekkel állnak elő.
Fried Katalin
ELTE TTK Matematikai Intézet
Matematikatanítás-módszertani Központ









