Egy feladat és ami róla az eszembe jutott...
A júniusi számban egy olyan algebra feladatot járunk körbe, amely sokféle témakör között teremt kapcsolatot. Bár leggyakrabban a teljes indukció tanítása során találkozunk vele, ismert algebrai átalakításokat felhasználó megoldása is, megközelíthetjük kombinatorikai eszközökkel és rekurzióval is. Cikkemben ezekre a módszerekre több változatot is be fogok mutatni. A feladat többek között a KöMaL 2020. márciusi számában is megjelent a „Gyakorló feladatsor emelt szintű matematika érettségire” cikkben.
A feladat
Bizonyítsuk be, hogy 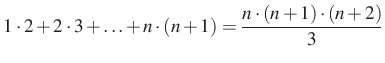 ; ahol
; ahol ![]() .
.
Használt összefüggések
A feladat megoldása során a következő ismert algebrai összefüggéseket használom:
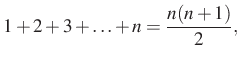
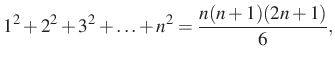
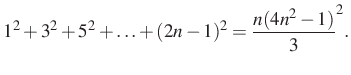
1. megoldás. Bontsuk fel a ![]() kifejezést,
kifejezést,
alakba és használjuk ezt fel a bal oldal összegezésére!
![$\displaystyle =\dfrac{n(n+1)(2n+1)}{6}+\dfrac{n(n+1)}{2}=\dfrac{n(n+1)}{2} \cdot \left[\dfrac{2n+1}{3}+1\right]=$](/images/stories/latex/utonmodon3/img12.png) |
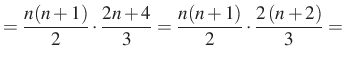 |
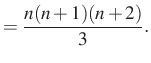 |
2. megoldás. Bontsuk fel ismét a ![]() kifejezést, de most a
kifejezést, de most a
alakba és használjuk ezt fel a bal oldal összegezésére!
![$\displaystyle =\dfrac{(n+1)(n+2)(2n+3)}{6}-\dfrac{(n+1)(n+2)}{2}=\dfrac{(n+1)(n+2)}{2} \cdot \left[\dfrac{2n+3}{3}-1\right]=$](/images/stories/latex/utonmodon3/img20.png) |
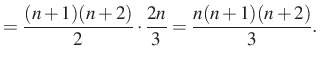 |
3. megoldás. Az ötletet a megoldáshoz ismét a ![]() kifejezés adja. Ezt a kifejezést én már láttam, méghozzá a
kifejezés adja. Ezt a kifejezést én már láttam, méghozzá a ![]() -ben:
-ben:
Tehát
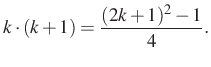
Alkalmazva
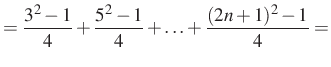 |
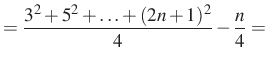 |
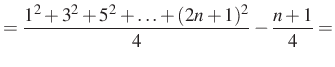 |
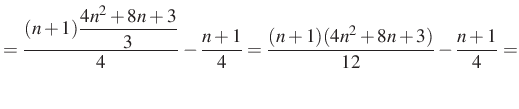 |
![$\displaystyle =\dfrac{(n+1)(4n^2+8n+3)}{12}-\left[\dfrac{3(n+1)}{12}\right]=$](/images/stories/latex/utonmodon3/img29.png) |
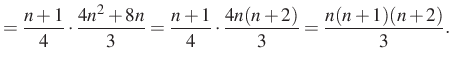 |
4. megoldás. Az ötletet a megoldáshoz ismét a ![]() kifejezés adja. Ezt a kifejezést én már láttam, méghozzá a
kifejezés adja. Ezt a kifejezést én már láttam, méghozzá a ![]() -ben:
-ben:
Tehát
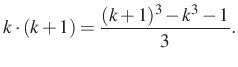
Alkalmazva
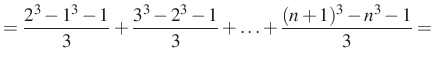 |
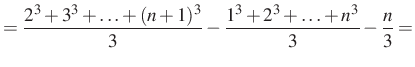 |
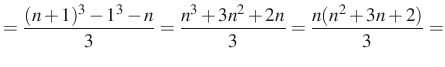 |
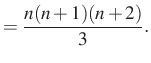 |
5. megoldás. Az ötletet a megoldáshoz ismét a ![]() kifejezés adja. Itt két egymás utáni szám van összeszorozva, de az ezen számok előtti és utáni két szám különbsége
kifejezés adja. Itt két egymás utáni szám van összeszorozva, de az ezen számok előtti és utáni két szám különbsége ![]() , azaz
, azaz ![]() . Használjuk ezt:
. Használjuk ezt:
![$\displaystyle =\dfrac{3k\cdot (k+1)}{3}=\dfrac{\left[(k+2)-(k-1)\right]k\cdot (k+1)}{3}=$](/images/stories/latex/utonmodon3/img40.png) |
|
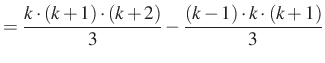 |
Ezt az azonosságot alkalmazzuk ![]() -től
-től ![]() -ig:
-ig:
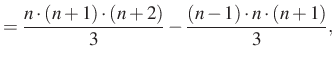 |
|
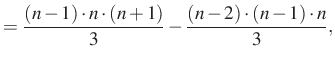 |
|
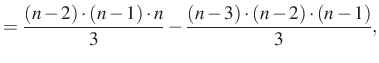 |
|
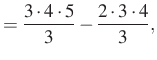 |
|
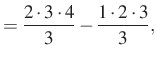 |
|
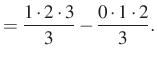 |
Összeadva a felírt egyenleteket, a jobb oldalon két kifejezés kivételével minden kétszer szerepel, a két kifejezés egymás ellentettje, ezért kapjuk:
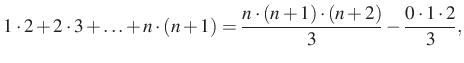
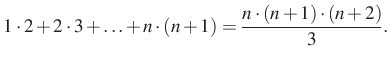
6. megoldás. Az ötletet a megoldáshoz ismét egy kifejezés, a ![]() adja. Ezek a bal oldal egymás utáni két tagja.
adja. Ezek a bal oldal egymás utáni két tagja.
Induljunk ki a bal oldalból, legyen ![]() és párosítsunk:
és párosítsunk:
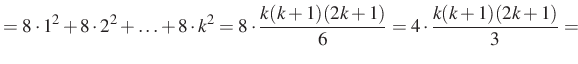 |
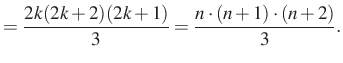 |
Legyen most ![]() , ekkor
, ekkor
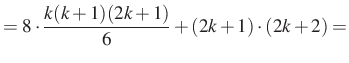 |
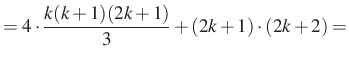 |
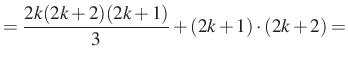 |
![$\displaystyle =(2k+1)\cdot (2k+2)\cdot\left[\dfrac{2k}{3}+1\right]=$](/images/stories/latex/utonmodon3/img72.png) |
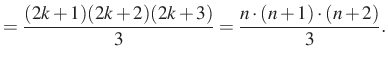 |
7. megoldás. Ennyi algebra megoldás után nézzünk most valami mást!
Tekintsük a következő feladatot:
Adott ![]() különböző magasságú diák, közülük 3 diákot választunk ki. Hányféleképpen tudjuk ezt megtenni?
különböző magasságú diák, közülük 3 diákot választunk ki. Hányféleképpen tudjuk ezt megtenni?
Adunk rá 2 megoldást.
I. megoldás
Mivel a diákok különbözőek, kiválasztási sorrendjük nem érdekes, 1 diák csak egyszer választható ki, ezért ez egy ismétlés nélküli kombinációs feladat, aminek a megoldása
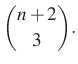
II. megoldás
Állítsuk a diákokat magassági sorrendbe.
A legkisebb diákot tekintve 2 eset van, vagy szerepel a kiválasztottak között, – ez 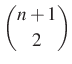 eset – vagy nem.
eset – vagy nem.
Ha a legkisebb nem szerepel a kiválasztottak között, akkor vegyük a második legkisebbet. Az ő szemszögéből is most két eset van, vagy szerepel, – ez ![]() eset – vagy nem.
eset – vagy nem.
és így tovább az utolsó 3 diákig, azaz ![]() -ig.
-ig.
Tehát a lehetséges kiválasztások száma
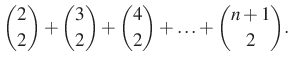
Két megoldást is adtunk a feladatra, a végeredmény ugyanaz:
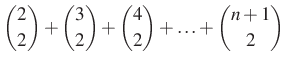 |
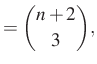 |
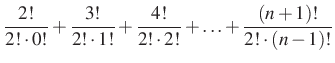 |
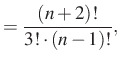 |
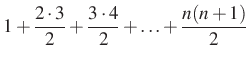 |
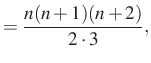 |
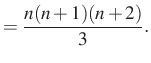 |
8. megoldás. Ismét egy kombinatorikus megoldást adunk.
Tekintsük a következő feladatot, amit a 7. megoldásánál is néztünk:
Adott ![]() különböző magasságú diák, közülük 3 diákot választunk ki. Hányféleképpen tudjuk ezt megtenni?
különböző magasságú diák, közülük 3 diákot választunk ki. Hányféleképpen tudjuk ezt megtenni?
A feladat megoldása.
Mivel a diákok különbözőek, kiválasztási sorrendjük nem érdekes, 1 diák csak egyszer választható ki, ezért ez egy ismétlés nélküli kombinációs feladat, aminek a megoldása
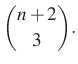
Alakítsuk át kifejezésünket, közben használjuk a binomiális együtthatókra igaz képzési szabályt,
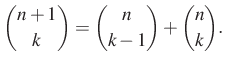
Kiindulunk a kapott végeredményből és a szabályt használva alakítunk:
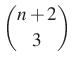 |
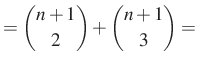 |
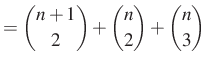 |
|
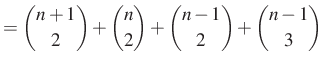 |
|
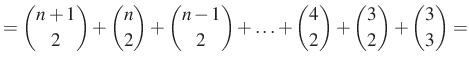 |
|
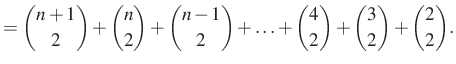 |
Azaz kaptuk, hogy
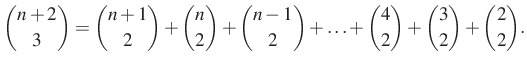
Most alakítsuk a kapott azonosságot a 7. megoldáshoz hasonlóan!
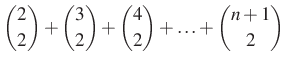 |
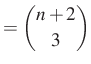 |
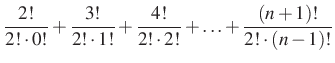 |
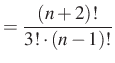 |
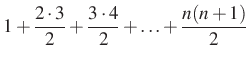 |
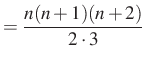 |
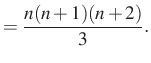 |
9. megoldás. A megoldás a „szokásos”. Teljes indukcióval bizonyítunk!
I. eset
Nézzük meg, hogy teljesül-e a bizonyítandó állítás ![]() esetre:
esetre:
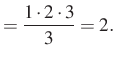 |
A vizsgált esetre teljesül az állítás.
II. eset
Tegyük fel, hogy ![]() -ra tejesül, hogy
-ra tejesül, hogy
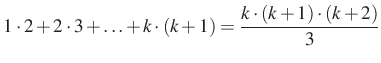
III. eset
Nézzük az ![]() esetet, induljunk ki a bizonyítandó állítás bal oldalából:
esetet, induljunk ki a bizonyítandó állítás bal oldalából:
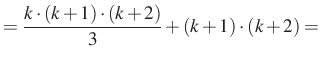 |
|
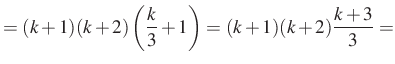 |
|
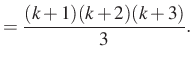 |
Azaz
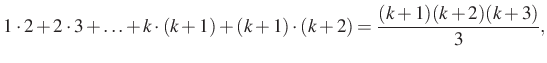
és ezt akartuk kapni, tehát a bizonyítás kész.
10. megoldás. És végül nézzünk most egy „kemény” megoldást, kezeljük a feladatot rekurzív módon. Legyen
egy sorozat eleme. Ekkor rekurzív módon megfogalmazva a feladatot:
Átírva a sorozatot:
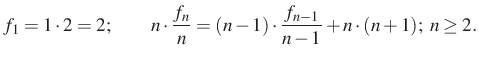
Vezessünk be új sorozatot: 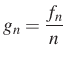 . Ekkor a keresett sorozat
. Ekkor a keresett sorozat
A ![]() sorozatot keressük
sorozatot keressük ![]() alakban.
alakban.
Ezt használva,
rendezve
Ha úgy választjuk meg ![]() ,
, ![]() és
és ![]() értékét, hogy a megjelölt kifejezés nulla minden
értékét, hogy a megjelölt kifejezés nulla minden ![]() értékére, akkor egyszrű lesz a helyettesítés
értékére, akkor egyszrű lesz a helyettesítés ![]() sorozatra. Mivel a kifejetés másodfokú, ezért ez csak akkor lesz minden értékre nulla, ha az együtthatói nullák, azaz
sorozatra. Mivel a kifejetés másodfokú, ezért ez csak akkor lesz minden értékre nulla, ha az együtthatói nullák, azaz
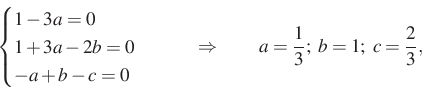
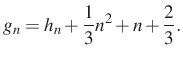
Tehát a ![]() sorozatra
sorozatra
A képzési szabályt felírva:
Visszafelé követve az egyenleteket adódik, hogy
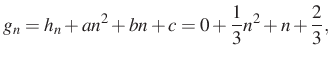
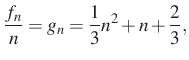
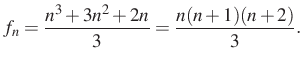
Visszacsatolás
Az Úton-módon 1. cikkében levő feladattal kapcsolatban többen is jelezték, hogy az már kitűzésre került a Matematika Tanítása folyóiratban és az 1986 évi 4. számban jelentek is meg megoldások. Az ott szereplő 4 megoldás közül most Róka Sándor megoldását ismertetem az eredeti leírással. Róka Sándor bemutatása – úgy gondolom – nem szükséges, ismeretterjesztő matematikakönyveiről közismert.
Emlékeztetőül a feladat: Az ![]() háromszögben
háromszögben ![]() és
és ![]() . Az
. Az ![]() oldal
oldal ![]() -n túli meghosszabbításán vegyük fel a
-n túli meghosszabbításán vegyük fel a ![]() pontot úgy, hogy
pontot úgy, hogy ![]() teljesüljön. Számítsuk ki az
teljesüljön. Számítsuk ki az ![]() nagyságát.
nagyságát.
Róka Sándor megoldása
Emeljünk az ![]() oldalra kifelé
oldalra kifelé ![]() szabályos háromszöget.
szabályos háromszöget.
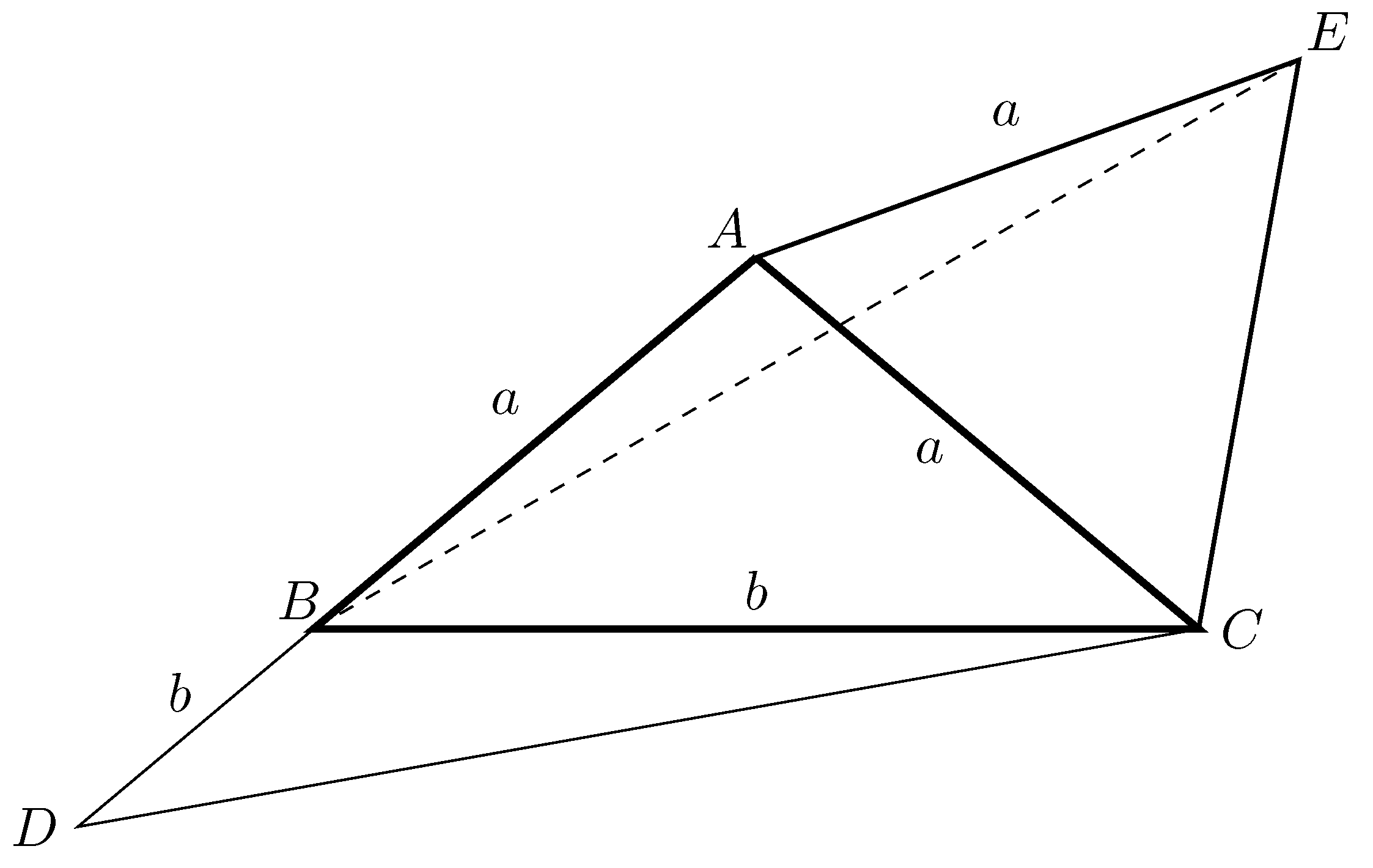
Az ![]() egybevágó a
egybevágó a ![]() -gel, mert
-gel, mert ![]() ,
, ![]() és
és ![]() . Mivel
. Mivel ![]() egyenlő szárú és szárszöge
egyenlő szárú és szárszöge ![]() , így
, így ![]() , tehát
, tehát ![]() és
és ![]() . A
. A ![]() szögei tehát:
szögei tehát: ![]() ,
, ![]() és
és ![]() .
.
Az Úton-módon 2. cikkében levő feladattal kapcsolatban is érkezett visszajelzés. A levélíró Laborczi Zoltán, aki a Győri Révai Miklós Gimnáziumban érettségizett 1967-ben és azon évben az IMO csapatnak is tagja volt IV. osztályosként és III. díjat nyert. Most matematikus, nyugdíjas informatikus.
Emlékeztetőül a feladat: Az ![]() szabályos háromszög
szabályos háromszög ![]() oldalának felezőpontja
oldalának felezőpontja ![]() . A
. A ![]() szakasz azon belső pontja a
szakasz azon belső pontja a ![]() pont, amelyre az
pont, amelyre az ![]() szög 90 fokos. A
szög 90 fokos. A ![]() szakasz azon belső pontja az
szakasz azon belső pontja az ![]() pont, amelyre a
pont, amelyre a ![]() és a
és a ![]() szakaszok hossza egyenlő. Hány fokos az
szakaszok hossza egyenlő. Hány fokos az ![]() szög?
szög?
Laborczi Zoltán megoldása
A 4. megoldáshoz hasonlóan tükrözzük az ![]() háromszöget a
háromszöget a ![]() pontra.
pontra.
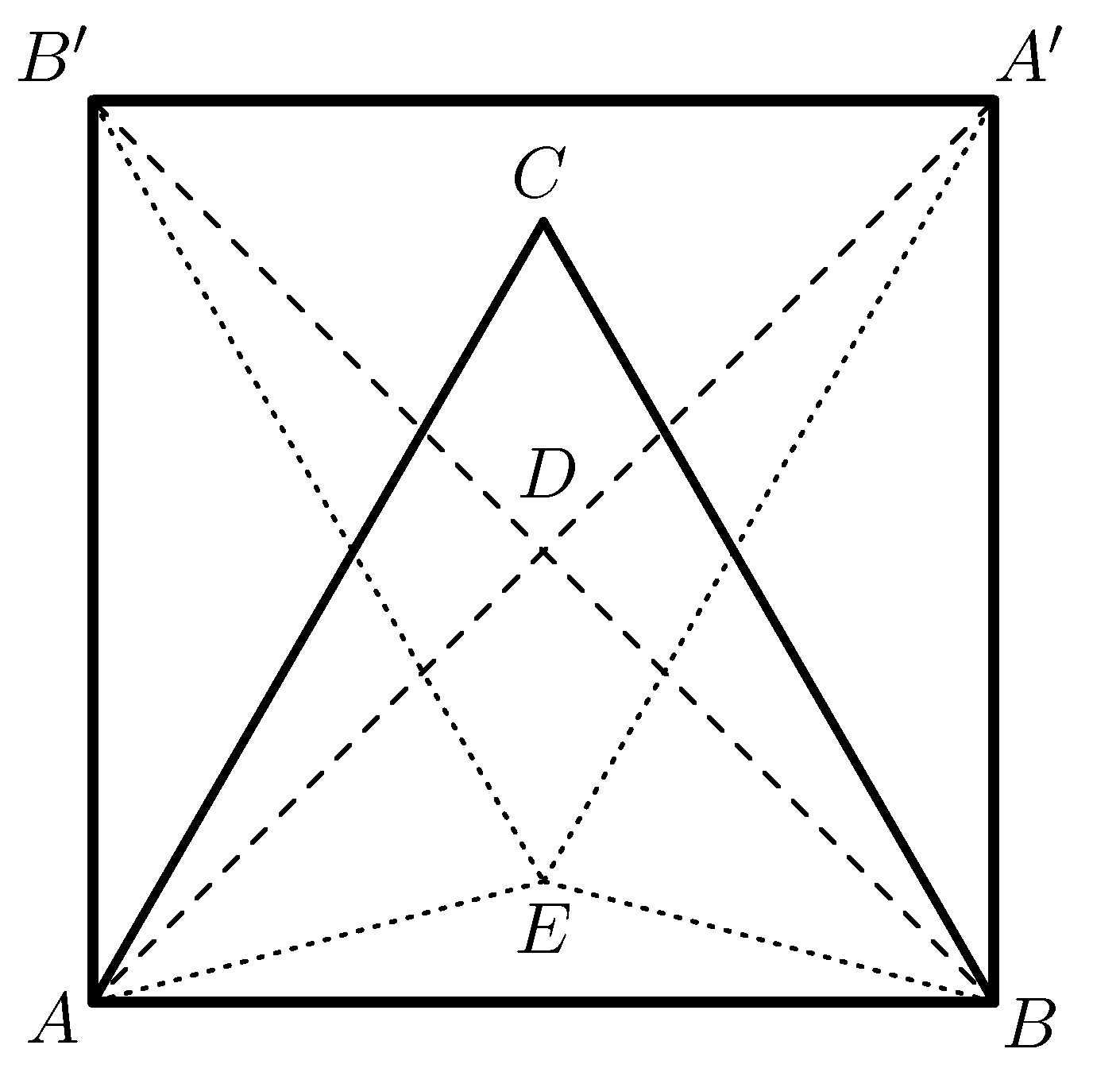
Ekkor a ![]() tükörképe
tükörképe ![]() . Az így kapott
. Az így kapott ![]() négyszög négyzet, hiszen átlói merőlegesek és egyenlő hosszúak. Az
négyszög négyzet, hiszen átlói merőlegesek és egyenlő hosszúak. Az ![]() szabályos háromszög tükörképe az
szabályos háromszög tükörképe az ![]() háromszög, szintén szabályos. Az
háromszög, szintén szabályos. Az ![]() háromszög egyenlő szárú, amelyben az
háromszög egyenlő szárú, amelyben az
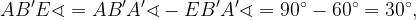
így a háromszög alapszögei ![]() -osak, tehát
-osak, tehát
Az ![]() pontnál lévő szögek összege
pontnál lévő szögek összege ![]() , így a keresett szög:
, így a keresett szög:
Zárszó
Kedves Olvasó! Ha egy másik „szép” megoldást talál, kérem, küldje el nekem a Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát. e-mail címre. Ezeket az újabb megoldásokat összegyűjtve időnként (terveim szerint) szintén megmutatnám.









