Bevezetés
Az előző részben általánosságban ismerkedhetettünk meg az okostelefonok használatának előnyeivel. Ebben a részben az általánosságokat magunk mögött hagyva a gráfelméletre fogunk koncentrálni. Olyan alkalmazásokat ismerhetünk meg, amelyek segítik mind a tanárok, mind pedig a diákok munkáját a matematika ezen területének tanulása, illetve tanítása során.
A gráfelmélet közoktatásban betöltött szerepe jelenleg nem túl jelentős. Ennek ellenére a matematikaoktatás egy olyan területéről beszélünk, ahol az érintőképernyő igazán jól kihasználható és valóban hozzá tud adni a tanórához.
Euler-út, Euler-kör
A probléma története, hogy a poroszországi Königsberg városban (most Kalinyingrád, Oroszország) hét híd ívelt át a várost átszelő Prégel folyón úgy, hogy ezek a folyó két szigetét is érintették. A königsbergiek azzal a kérdéssel fordultak Eulerhez, vajon végig lehet-e menni az összes hídon úgy, hogy mindegyiken csak egyszer haladjanak át, és egyúttal visszaérjenek a kiindulópontba? 1736-ban Euler bebizonyította, hogy ez lehetetlen.
A fenti problémából született az Euler-kör és Euler-út problémája. Ezekre rengeteg játékot találunk mindegyik alkalmazásboltban. Android, illetve iOS eszközökön is a One Touch Drawing névre hallgató alkalmazás az egyik legjobb ezek közül.
One touch Drawing - Android - https://play.google.com/store/apps/details?id=com.ecapycsw.onetouchdrawing
One touch Drawing - iOS - https://itunes.apple.com/hu/app/one-touch-drawing/id494856551?mt=8
Az alkalmazás bár ingyenes, de reklámokat tartalmaz. A reklámokat tartalmazó játékok esetében sajnos sokszor tapasztalható, hogy véletlenül rányom az ember a hirdetésre, vagy az elterelheti a diákok figyelmét. Ezért ilyen esetekben a tanárnak kiemelten oda kell figyelni, hogy a diákok ne kalandozzanak el.
A játék kb. 600 pályán át rajzoltat velünk Euler-utakat. A feladat nem nevesíti, hogy Euler-bejárásokat kér a játékosoktól. Ahogy a neve is mutatja, az a feladat, hogy a megjelenő kis ábrákat úgy rajzoljuk le újra, hogy nem emeljük közben fel a ceruzánkat/ujjunkat. Ha esetleg valaki nem ismeri az Euler-út létezésének szükséges és elégséges feltételét, akkor is rá fog jönni arra, mire végigrajzolja a pályákat.
 Korosztály
Korosztály
Az alkalmazás akár már 4-5 éves gyermekek számára is ajánlott, ekkor természetesen nincs még szükség Euler-utakról beszélni. Azonban ugyanúgy érdekes lehet a játék a 16-18 évesek számára is, akik a játék segítségével megsejthetik a témakörhöz szükséges tételeket.
Tanórai használat
Az alkalmazást órán szoktam bemutatni a diákjaimnak. Ezután házi feladatnak adom fel a játékot. Kötelező megcsinálni mindenkinek 20 pályát, de aki eljut 100-200 pályáig, az jutalomban részesül. Így a diákok többsége értelmes és gondolkodtató játékkal tudja tölteni a szabadidejét. Sőt, többen leragadnak az alkalmazásnál és játszanak vele később is, amikor már nem is kötelező.
Síkbarajzolhatóság
A másik híres gráfelméleti probléma a síkbarajzolhatóság problematikája. Itt az a kérdés, hogy az előttünk megjelenő gráfot le tudjuk-e úgy rajzolni, hogy az élei ne keresztezzék egymást.
Erre is rengeteg olyan alkalmazás található, amelynek segítségével ez a probléma is játékosan tálalható a diákok elé.
Untangle - Android - https://play.google.com/store/apps/details?id=air.App2Eleven.LogicGamePuzzlesUntangle
Untangle - iOS - https://itunes.apple.com/us/app/untangle-logic-games/id1100124116?mt=8
Az Untangle alkalmazás is reklámokat tartalmaz. Ezekre sajnos oda kell figyelni, azonban segítségével a síkbarajzolhatóság kérdésköre egy játékká válik, ahol több „összegabalyított” gráfot kell rendbetennünk. Itt is rengeteg pályán át bizonyíthatjuk, hogy meg tudunk birkózni a problémával. Ahogy haladunk előre, úgy nő a csúcsok száma, s válik egyre bonyolultabbá a gráf éleinek kibogozása. 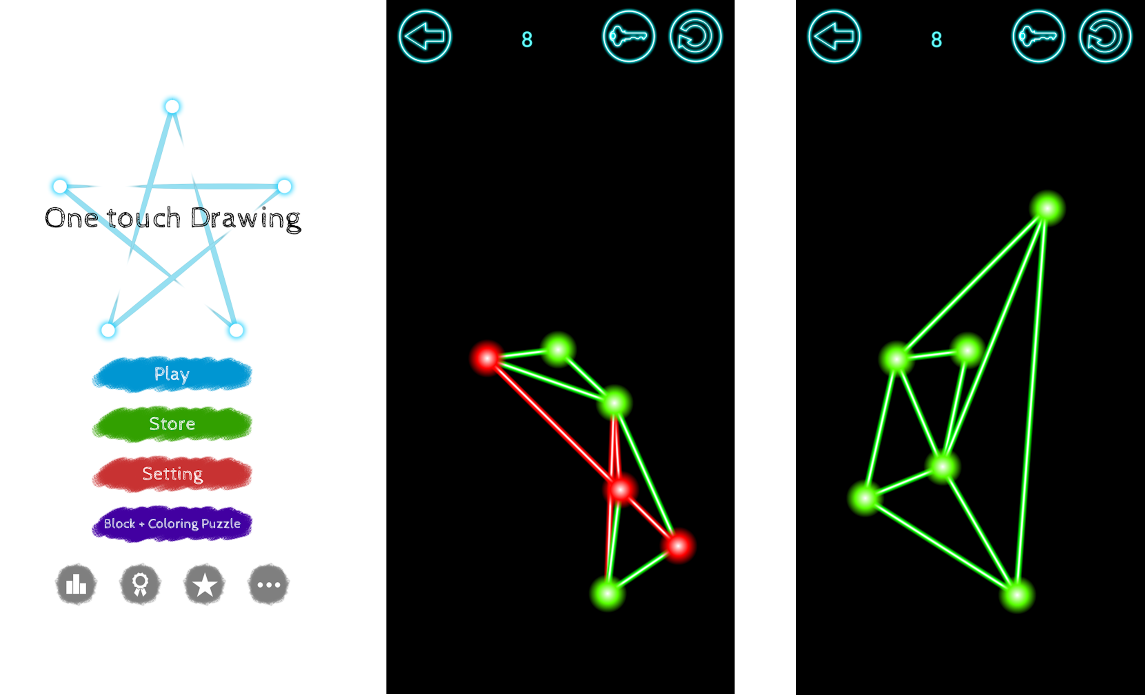
A játék a keresztező éleket pirossal, a már „tisztázottakat” zöld színnel jelzi. Így vizuálisan is jól látható, mely élek keresztezik még egymást. A kibogozást a csúcsok áthelyezésével végezhetjük el. Ez pedig az érintőképernyőn könnyen megvalósítható.
Korosztály
Ezt a játékot mutattam már 4 éves gyermekemnek is, aki egy darabig el is jutott benne, s számára is élvezhető volt a gráf kibogozása. Természetesen itt sem gráfokról és élekről beszéltünk, s a fokszám elnevezés sem fordult elő. Azonban a játék 12. osztályos diákjaimnak is élvezetes volt.
Tanórai használat
Mivel a síkbarajzolhatóság nem középszintű érettségi követelmény, így inkább emelt szinten ajánlom az alkalmazással való ismerkedést. Maga a probléma, ahogyan azt láthattuk, középszinten is belefér a tananyagba.
Érdekességként szokott előkerülni a síkbarajzolhatóság a gráfelmélet témakörében. Ezelőtt táblára rajzoltam, s a diákok próbálták a gráfot a füzetükben „kicsomózni”. Azonban egy-egy füzetben lévő gráf összevetése a táblán lévővel lassú és nehéz feladat a tanár számára is. Az érintőképernyő viszont erre ideális. Hasonlóan a One Touch Drawing alkalmazáshoz, jutalomért fel szoktam adni szorgalmi feladatként.
Négyszín-tétel
A négyszín-tételre meglepő módon jóval kevesebb alkalmazás érhető el az alkalmazásboltokban, mint Euler, illetve a síkbarajzolhatóság problémájára. Ezek közül a legjobb talán a
Fast Fill - Android - https://play.google.com/store/apps/details?id=be.ghavelan.four
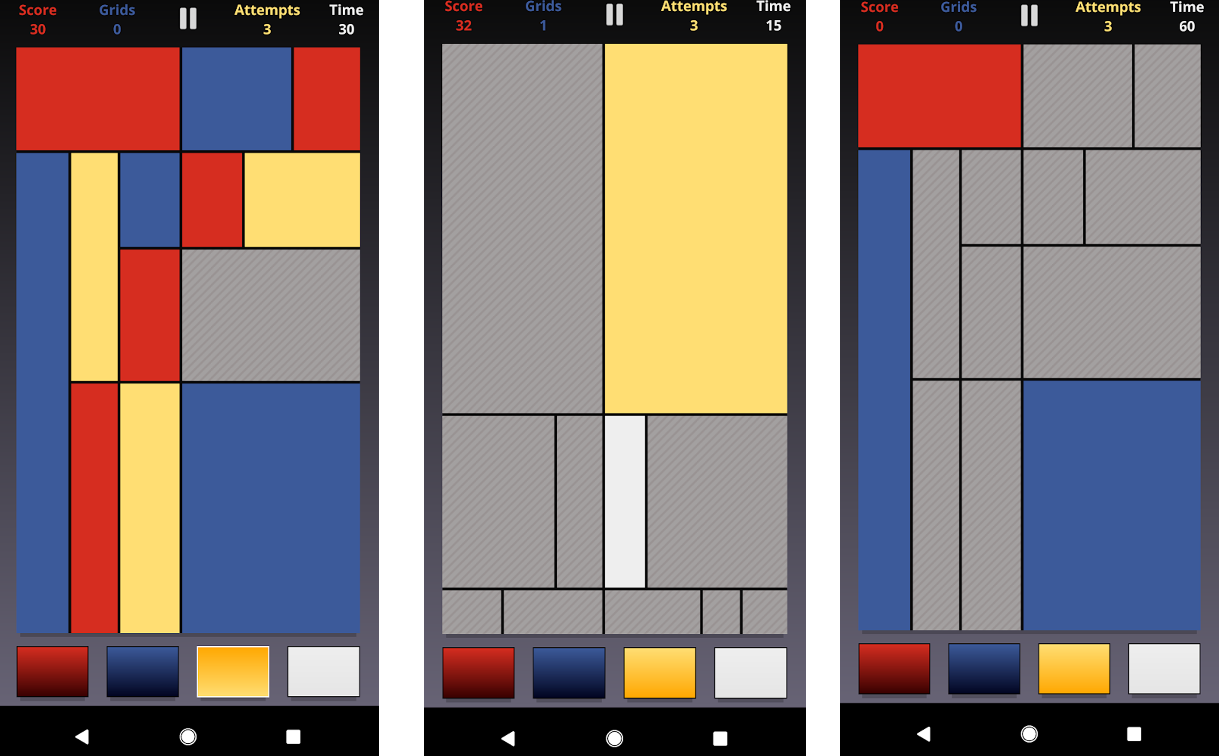
Ebben az alkalmazásban kék, piros, sárga és fehér színekkel kell kiszínezni egy vásznat. Az alkalmazás nem elsősorban a négyszín-tétel gyakoroltatására készült. De játék közben hamarosan el fognak jutni a diákok oda, hogy megkérdőjelezzék, elegendő-e a négy szín. Ezen a ponton pedig megjelenik a tétel kimondása és bizonyítása iránti vágy.
Korosztály
Ez is olyan alkalmazás, amit már egy ötéves gyerek is élvezettel tud kezelni. Az ő esetében még nem lesz tudatos a színezés. Érdekessé matematika fakultáción válhat, amikor a négyszín-tételről tanulnak a diákok.
Tanórai használat
Jó lehetőség az alkalmazás segítségével felvezetni a témát. A diákok színeznek, s felmerül a kérdés, hogy lehet-e olyan palettát adni, ahol kevés a 4 szín, illetve lehet-e három színnel színezni.
Utazóügynök-probléma
A negyedik izgalmas gráfelméleti probléma az utazóügynök-probléma, amire a Quick Route alkalmazás ad játékos feladatokat.
Quick Route — iOS - https://itunes.apple.com/us/app/quick-route-a-puzzle-that-requires-thought-to-solve/id882744410?mt=8&at=11lxMa
Van több Androidos alkalmazás is, azonban a Quick Route azzal emelkedik ki a mezőnyből, hogy az igényes kialakítás mellett nem tartalmaz reklámokat. És ingyenes.
Azonban az utazóügynök-probléma megoldásához nem feltétlen ideális ez a játék. A probléma szemléltetésére talán alkalmas, bár erre talán inkább egy utazási iroda honlapját ajánlanám.
Összefoglalás
Az ebben a részben megismert alkalmazások alkalmasak arra, hogy a gráfelmélet legismertebb kérdéseivel megismerkedjenek a diákok. A játékok segítségével az ismerkedés nem a megszokott definíció, tétel, hanem a felfedeztető, játékos matematikaoktatást teszi lehetővé. A sorozat folytatásában további alkalmazásokat fogunk megismerni.
Koren Balázs
Budapesti Fazekas Mihály gyakorló Általános Iskola és Gimnázium
ELTE TTK Matematikatanítási és Módszertani Központ