Világéletemben szerettem feladatokat, rejtvényeket megoldani. Tanárként sokat foglalkozom a felső tagozatos tanulók versenyeztetésével matematika tantárgyból. A versenyfelkészítés teljesen más munkát követel meg tőlünk, mint egy szokványos tanóra megtartása. De sokkal érdekesebb is! A gyerekeknek olykor igencsak meglepő ötleteik vannak, olyan megoldásokat adnak egy-egy feladatra, amire az ember felnőtt fejjel nem is gondolna. Többek között ezért is nagyon jó általános iskolában tanítani, mert sokat tanulhatok a kreatív diákoktól.
Az alábbiakban egy olyan munka néhány eredményét mutatom be, mely konkrét feladatok megoldásán keresztül elemzi különböző életkorú általános iskolás tanulók matematikai gondolkodásmódját. Néhány olyan feladatot válogattam ki a vizsgálathoz, amelyeket többféle módon is meg lehet oldani. A résztvevők hatodik, hetedik, nyolcadik osztályos diákok, akik a matematikát emelt szinten, heti 5 órában tanulják. Úgy gondolom, érdeklődésre tarthat számot néhány érdekes ötlet, feladatmegoldás ismertetése.
Számjegyes feladat: A 6****7 egy hatjegyű számot jelöl. Írjunk számjegyeket a *-ok helyére úgy, hogy bármely három egymást követő számjegy összege 20 legyen! Mennyi a kapott hatjegyű szám számjegyeinek összege? (Zrínyi 2010., 3. osztály, megyei 20. feladat).
Természetesen a feladat elolvasása után általában a tanulók először próbálkoznak a *-ok helyére megfelelő számjegyeket beírni. Az ügyesebbek később jönnek rá arra, hogy erre nincs is szükség.
Már egy hatodikos tanulóban is felmerül az az ötlet, hogy „nem szabad túl sok eltérésnek lenni bármely 3 számban”. Egy hetedikes diák még ezt az ötletet is továbbvitte:
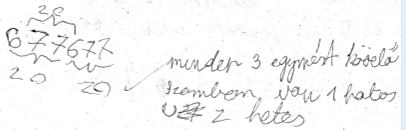
Életkori sajátosság, hogy a gyerekek a gondolatmenetüket még nem tudják teljesen részletesen leírni, így az indoklás hiányzik.
Egy nyolcadikos tanuló szép indoklást is megfogalmazott. Rájött arra, hogy a 677-et kétszer kell beírni. De az indoklása azért nem teljes, mert nem magyarázza meg, hogy az eredetileg ismert 6 és 7 számjegyek miként kerülhetnek egymás mellé.

Végül egy hetedikes kreatív, frappáns megoldása:

Duplázós feladat: Hányszorosára növekszik a 2000 · 2000 + 2000 · 2000 összeg, ha a 2000 helyére mindenütt a kétszeresét írjuk? (Zrínyi 1994., 5. osztály, országos 7. feladat alapján: az eredeti feladatban az évnek megfelelően az általam használt 2000 helyett 1994 szerepel).
A választásom azért esett erre a feladatra, mert kíváncsi voltam, hogy a tanulók hogyan számolnak ekkora nagyságrendű számokkal, illetve hogy találnak-e könnyebb megoldási módot. És mivel a gyerekek kreatívak, természetesen találtak.
Már hatodikos tanulók is alkalmazták a megoldáshoz a hatványozást. Azok a diákok, akik nem számoltak ezekkel a nagy számokkal, többnyire lejátszották a feladatot „kicsiben”, ami nagyfokú kreativitásról és kiváló algebrai érzékről tanúskodik.

Családtagos feladat: Egy öttagú családban a családtagok életkorai egész számok, és az életkorok összege 82 év. Az apa két évvel idősebb az anyánál, és éveinek háromszorosához 1-et hozzáadva 100-at kapunk. Mennyi volt 2 évvel ezelőtt a családtagok életkorának összege, ha a legkisebb gyerek 4 évesnél idősebb, és a gyerekek között nincsenek ikrek? (Zrínyi 1995., 7. osztály, megyei 15. feladat).
Ez a feladat ismét tipikus esete annak, hogy az ember elkezd számolni. És mikor már legalább másodjára olvassa el a feladat szövegét, akkor jön rá arra, hogy nem kell az életkorokat kiszámolni.
A tanulók általában kiszámolták a szülők életkorát. Sokan akkor jöttek rá, hogy nem is ez a feladat kérdése. Lássunk egy hatodikos ötletet:
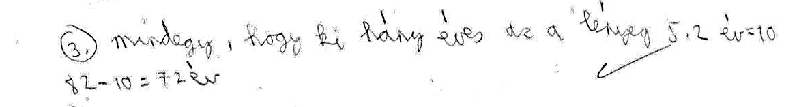
Nyomon követhető a diákok munkájából a gondolatmenetük is. Ebben a megoldásban még az önkritika is megjelenik:

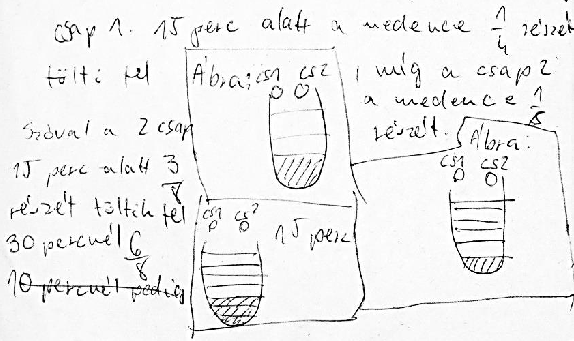
Medencés feladat: Egy medencébe 2 csapon keresztül folyhat a víz. Az üres medencét egyedül az első csap használatával 1 óra alatt, egyedül a második csap használatával 2 óra alatt lehet teljesen feltölteni. Hány perc alatt lesz tele az üres medence, ha egyszerre mindkét csapot kinyitjuk? (Zrínyi 2005., 7. osztály, országos 8. feladat).
Ez a feladattípus a 8. osztályos tananyagban, az egyenletek témakörében szerepel, de a felmérés időpontjában a diákok ezt még nem tanulták. Arra voltam kíváncsi, hogy a tanulók az együttes munkára vonatkozó szöveges feladatok megoldási módjának ismerete nélkül ki tudják-e logikázni a megoldást, és milyen módon teszik ezt.
Már a hatodikosok is ügyesen okoskodtak: konkrét egységet választottak: 60 litert, vagy 120 litert. Természetesen itt még hiányzik az általánosítás tetszőleges űrtartalomra.
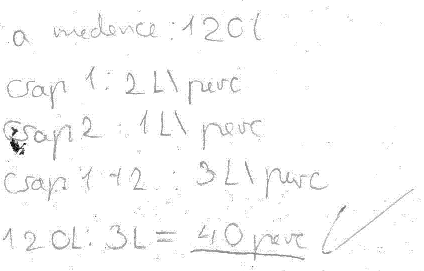
Általában a rajz is sokat segít az okoskodásban. Következzen egy hetedikes feladatmegoldása:
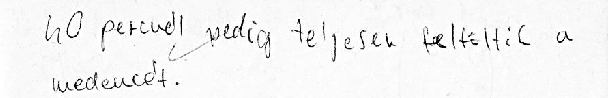
A nyolcadikosoknál pedig már komoly megfontolások is olvashatók:
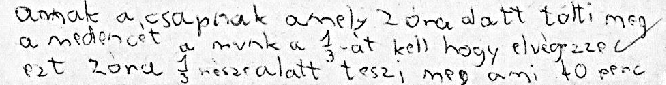
E néhány példa alapján is látható, hogy tanítványaink mennyire kreatívak, és milyen jó ötletekkel tudnak bennünket, tanárokat is meglepni. Az a fontos, hogy hagyjuk őket gondolkozni és ne lőjük le a poént. Ne mi akarjuk rögtön és kizárólagosan megtanítani nekik az általunk jónak ítélt eljárásokat. Hiszen a gyerekek egyszerű és tiszta gondolkodása lehet, hogy sokkal frappánsabb megoldást eredményez!
Dr. Kovácsné Pető Andrea
a Debreceni Egyetem Kossuth Lajos Gyakorló Általános Iskolájának tanára









