Fixponttételek és alkalmazásaik

Bessenyei Mihály, Páles Zsolt: Fixponttételek és alkalmazásaik (Typotex, Budapest, 2023)

Ezt a könyvet a szerzők a tudományterület első magyar nyelvű monográfiájának szánták. Kis jóindulattal ugyan talán megállja a helyét az a kijelentés, hogy Hegedüs Miklós és Zalai Ernő „Fixpont és egyensúly a gazdasági modellekben” című könyvének második része (Közgazdasági és Jogi Könyvkiadó, Budapest, 1978) a maga bőséges anyagával és még bőségesebb irodalomjegyzékével volt a szakterület első magyar nyelvű monográfiája, de mindenképp örvendetes egy olyan újabb monográfia megjelenése, amely már az utóbbi fél évszázad eredményeiből is tudott válogatni, és amelyben sokkal többféle alkalmazás jelenik meg, mint Hegedüs és Zalai könyvében. Ha a Kedves Olvasó tanult már egy kevés matematikát valamelyik egyetemen, akkor bízhat benne, hogy meg fogja érteni a könyvet, vagy annak legalábbis nagy részét, hiszen a szerzők a témák egy részéhez a szükséges segédapparátust is gondosan kiépítették.

I. Iteratív fixponttételek és alkalmazásaik

A könyv első részében szereplő fogalmak közül talán a legfontosabb a kontrakció fogalma. Tetszőleges 1-nél kisebb pozitív 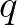$q$ szám esetén értsünk 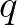$q$ -kontrakción olyan 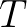$T$ leképezést, amelynek értelmezési tartománya valamely 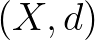$(X,d)$ metrikus térben lévő 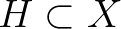$H\subset X$ halmaz, értékei 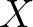$X$ -ben vannak, és amelyre minden 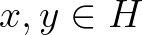$x,y\in H$ esetén 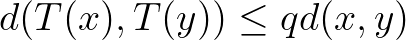$d(T(x),T(y))\leq qd(x,y)$ teljesül (a szerzők terminológiája: kontrakció 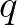$q$ faktorral vagy 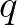$q$ modulussal), míg a kontrakció szó jelentése legyen az, hogy 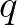$q$ -kontrakció valamilyen 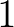$1$ -nél kisebb pozitív 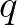$q$ számmal.

Az első két fejezetben a Banach-féle fixponttétel témakörének alapos diszkusszióját kapja az olvasó. Az alapos diszkussziónak az 1. fejezetbe eső részébe például beleértendők a szukcesszív approximációval képzett közelítő sorozattal kapcsolatban a közelítés mértékére vonatkozó becslések, beleértendő egy arra vonatkozó elégséges feltétel is (1.6. tétel), hogy egy 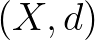$(X,d)$ teljes metrikus tér nyílt gömbjén értelmezett, és azt az 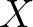$X$ -be képező kontrakciónak létezzék egyetlen fixpontja, továbbá beleértendő a fixponttétel néhány olyan általánosításának bemutatása is, amelyek a kontrakciós feltétel gyengítésével kaphatók.

A 2. fejezetben két olyan tétellel ismerkedhetünk meg, amelyek valamilyen értelemben a Banach-féle fixponttétel megfordításának, vagy egy következmény megfordításának tekinthetők. Röviden (és kissé pongyolán) fogalmazva mindkét esetben egy leképezés iteráltjaira vonatkozó feltételből lehet arra következtetni, hogy a leképezés kontrakció.

A 3. fejezetben arra látunk példákat, hogyan lehet alkalmazni a Banach-féle fixponttételt az analízisben fellépő különféle egyenletek egyértelmű megoldhatóságának bizonyítására. Konkrétabban fogalmazva, van itt szó Fredholm-féle és Volterra-féle integrálegyenletekről, közönséges differenciálegyenletekre vonatkozó kezdetiérték-feladatokról, függvényegyenletekről, Banach-tér egy nyílt részhalmazát Banach-térbe képező függvény segítségével felírt egyenletről. Az utóbbi témához tartozó inverzfüggvénytétel bizonyításában jut szerephez a fent említett 1.6. tétel.

A 4. fejezet a „Fraktálelmélet” címet viseli. Az, hogy miért kerülhet ez a téma egy fixponttételekről szóló könyvbe, rögtön a definícióból kiderül. Olyan definíciót olvashatunk itt, amely a fraktál fogalmát egy 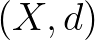$(X,d)$ metrikus térhez és 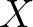$X$ -et önmagába képező függvények egy véges 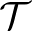$\mathcal{T}$ halmazához kapcsolja: ebben a kontextusban 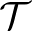$\mathcal{T}$ -fraktálon az 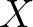$X$ -nek olyan nemüres kompakt 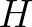$H$ részhalmazát értjük, amelyre

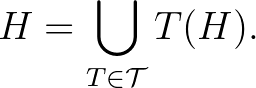
$\displaystyle H=\bigcup_{T\in\mathcal{T}}T(H).$

A fejezet fő eredménye Hutchinson tétele, amely azt állítja, hogy ha 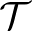$\mathcal{T}$ mindegyik eleme kontrakció, akkor létezik pontosan egy 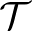$\mathcal{T}$ -fraktál. Ennek bizonyítása céljából a Banach-féle fixponttételt abban a metrikus térben lehet alkalmazni, amelyben az alaphalmaz elemei az 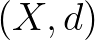$(X,d)$ metrikus tér nemüres kompakt részhalmazai, és amelyben a metrika a Hausdorff(–Pompeiu)-féle távolság. Ebben a metrikus térben mindenütt sűrű halmazt alkot azoknak a 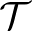$\mathcal{T}$ -fraktáloknak a halmaza, amelyek véges számú konstans leképezésből álló 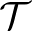$\mathcal{T}$ halmazhoz tartoznak. Ezt a tételt, amely egyszerű következménye annak, hogy az 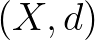$(X,d)$ tér minden kompakt részhalmaza teljesen korlátos, a szerzők a képfeldolgozás alaptételének nevezik, s a tétel megfogalmazása előtt kijelentik, hogy a fraktálelmélet egyik fontos alkalmazása a képek digitális tárolásához kapcsolódik. A fejezetet három példa, a Cantor-halmaz, a Sierpiński-szőnyeg, és a Menger-szivacs tárgyalása zárja.

Az 5. fejezetben metrikus terek helyett parciálisan rendezett halmazokról olvashatunk, kontrakciók helyett pedig monoton leképezésekről. A fejezet első tétele a teljesen elemi Knaster–Tarski-tétel, amely így szól: Tetszőleges halmaz hatványhalmazát önmagába vivő, tartalmazásra nézve monoton (növő) leképezésnek van fixpontja. Ezután megismerhetjük e tétel három általánosítását, majd e tételek néhány alkalmazását. Az első alkalmazás a számosságaritmetika alaptétele, ezt követi a közönséges differenciálegyenletek, a függvényegyenletek és a fraktálok témakörében egy-egy, illetve két tétel.

A 6. fejezetben fontos szerepe van az úgynevezett Bishop–Phelps-féle parciális rendezésnek, amelynek definíciója: adott 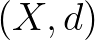$(X,d)$ metrikus tér és 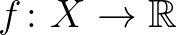$f\colon X\to\mathbb{R}$ esetén jelentse 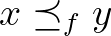$x\preceq_f y$ azt, hogy 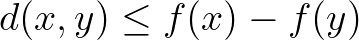$d(x,y)\leq f(x)-f(y)$ . A 6.1. tétel (Bishop–Phelps) azt állítja, hogy ha az 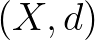$(X,d)$ metrikus tér teljes, 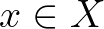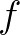$x\in X$ , $f$ pedig alulról korlátos és alulról félig folytonos, akkor az 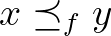$x\preceq_f y$ feltételnek eleget tevő 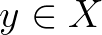$y\in X$ elemek között található olyan, amelyik maximális a 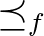$\preceq_f$ parciális rendezésre nézve. Ennek egyszerű következménye a Caristi-féle fixponttétel: ha 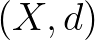$(X,d)$ teljes metrikus tér, 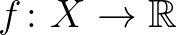$f\colon X\to\mathbb{R}$ alulról korlátos és alulról félig folytonos, 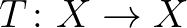$T\colon X\to X$ pedig teljesíti azt a feltételt, hogy minden 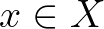$x\in X$ esetén 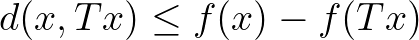$d(x,Tx)\leq f(x)-f(Tx)$ , akkor a 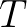$T$ leképezésnek van fixpontja. Ezután arról olvashatunk, hogy adott 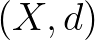$(X,d)$ metrikus tér és 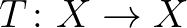$T\colon X\to X$ mellett, illetve adott 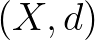$(X,d)$ metrikus tér és folytonos 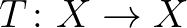$T\colon X\to X$ mellett milyen kapcsolatok vannak az alábbi állítások között:

1. a 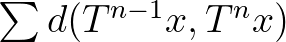$\sum d(T^{n-1}x,T^nx)$ végtelen sor minden 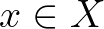$x\in X$ esetén konvergens,

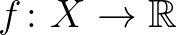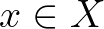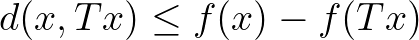2. létezik olyan alulról korlátos $f\colon X\to\mathbb{R}$ , amelyre minden $x\in X$ esetén $d(x,Tx)\leq f(x)-f(Tx)$ ,

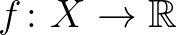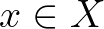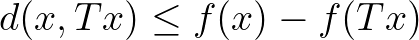3. létezik olyan alulról korlátos, alulról félig folytonos $f\colon X\to\mathbb{R}$ , amelyre minden $x\in X$ esetén $d(x,Tx)\leq f(x)-f(Tx)$ ,

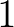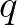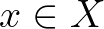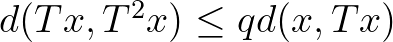4. létezik olyan $1$ -nél kisebb pozitív $q$ szám, amelyre minden $x\in X$ esetén $d(Tx,T^2x)\leq qd(x,Tx)$ .

A fejezet utolsó két szakaszában az Ekeland-féle variációs elvet és alkalmazásait, az utolsó alkalmazáshoz kapcsolódva pedig a Banach-féle nyíltleképezés-tétel Graves–Ljusztyernyik-féle nemlineáris kiterjesztésének témakörét ismerhetjük meg.

II. Topologikus fixponttételek és alkalmazásaik

A 7. és 8. fejezet témája a Brouwer-féle fixponttétel és annak néhány általánosítása. Brouwer tétele úgy szól, hogy ha 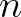$n$ pozitív egész, 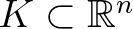$K\subset \mathbb{R}^n$ nemüres, konvex, kompakt halmaz és 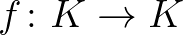$f\colon K\to K$ folytonos függvény, akkor 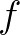$f$ -nek van fixpontja. Ennek a két legkönnyebben megfogalmazható általánosítása az 1. Schauder-féle fixponttétel, illetve a Tyihonov-féle fixponttétel. Az előbbi esetben az 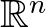$\mathbb{R}^n$ tér helyébe tetszőleges normált tér léphet, az utóbbi esetben pedig lokálisan konvex Hausdorff-féle topologikus vektortér. A Brouwer-tételnek azt a bizonyítását olvashatjuk, amely a Knaster–Kuratowski–Mazurkiewicz-lemmát használja, az utóbbi lemmát pedig a gráfelméleti terminológiával bizonyított kombinatorikus jellegű Sperner-lemmából vezetik le a szerzők. Schauder második fixponttétele egy olyan folytonos függvény fixpontjának létezését állítja, amelynek értelmezési tartománya nemüres, korlátos és zárt halmaz egy Banach-térben, értékkészlete pedig teljesen korlátos részhalmaza az értelmezési tartománynak. A Darbo–Szadovszkij-féle fixponttétel azt állítja, hogy ha itt az értelmezési tartomány nem kompakt, akkor a függvényről elég valamivel kevesebbet feltenni, éspedig azt, hogy legyen úgynevezett kondenzáló leképezés. A kondenzáló leképezés fogalmának értelmezése a Kuratowski-féle nemkompaktsági mérték fogalmán alapul. Az utóbbi fogalom definíciója a következő: egy metrikus tér 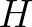$H$ részhalmazának nemkompaktsági mértéke azon 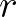$r$ pozitív számok halmazának legnagyobb alsó korlátja, amelyekre 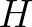$H$ lefedhető véges számú 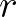$r$ sugarú nyílt gömbbel (ez tehát nem korlátos 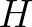$H$ esetén 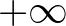$+\infty$ , teljesen korlátos 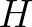$H$ esetén 0), míg a kondenzáló leképezésé: 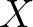$X$ Banach-tér és 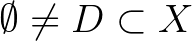$\emptyset\neq D\subset X$ esetén egy folytonos 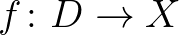$f\colon D\to X$ leképezést akkor nevezünk kondenzálónak, ha bármely korlátos, de nem teljesen korlátos 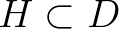$H\subset D$ esetén 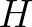$H$ nemkompaktsági mértéke nagyobb, mint 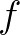$f$ szerinti képének nemkompaktsági mértéke. A 8. fejezet utolsó két tétele arra ad egy-egy elégséges feltételt, hogy affin, páronként felcserélhető leképezések osztályának létezzék közös fixpontja.

A 9. fejezetben a szerzők az előző két fejezet eredményeit a klasszikus analízis, a játékelmélet, a közönséges differenciálegyenletek, a funkcionálanalízis és a mértékelmélet egy-egy alapvető eredményének bizonyításához használják fel.

A 10. fejezet zérushelytételekről és halmazértékű leképezések fixpontjairól szól (egy halmazértékű 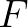$F$ függvény fixpontja az értelmezési tartományának olyan 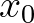$x_0$ eleme, amelyre 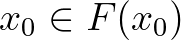$x_0\in F(x_0)$ . Olvashatjuk itt többek között a Tyihonov-féle fixponttétel halmazértékű általánosításának bizonyítását.

A 11. fejezet a fokszámelmélet alapjait foglalja össze. Az elmélet alapjául szolgáló Leray–Schauder-tétel bizonyításának rövid vázlata után három alkalmazásról olvashatunk.

III. Még néhány apróság

A könyv olvasói a szorosabb értelemben vett matematikai ismereteken kívül néhány további érdekes információhoz is hozzájuthatnak. Például:

Hogy lehet kapcsolatba hozni a gömbfelületen értelmezett folytonos vektormező gyökhelyének létezéséről szóló Poincaré-tételt a Jupiter bolygó „Vörös Folt”-jával?

Mi köze van a Brouwer-féle fixponttételnek a palacsintasütéshez?

Mit mond Neumann János azoknak, akik nem értenek egyet azzal a véleményével, hogy a matematika egyszerű?

Végül, de nem utolsó sorban megtudhatjuk, hogy a szerzők költői lelkek (vagy legalább az egyik szerző költői lélek), erről tanúskodik az, amit az Előszó utolsó előtti bekezdésében az „egykori szolgálóleányból csodálatos hercegnővé” előlépett matematikáról, illetve annak szépségéről olvashatunk.

Szilágyi Tivadar

ny. egyetemi docens, ELTE TTK Matematikai Intézet