Tizenegyedikesként felutazhattam a Rényi Alfréd Matematikai Kutatóintézetbe a „Mi a matematika, kik a matematikusok?” rendezvényre, ahol először hallottam arról, hogy valaminek lehet például 1,585 a dimenziója. Máig emlékszem, mennyire lenyűgözött; az esemény jelentős szerepet játszott abban, hogy eldöntöttem: matematikus leszek. De még éveknek kellett eltelnie, hogy megértsem: a fraktálok nem csak szépek, hanem „hasznosak” is. A tenger partvidékének vonalát vagy a karfiol felületét vizsgálva is felbukkannak a fraktálok, de a közgazdaságtanban (tőzsdei folyamatok), az elektronikában vagy éppen az agydaganatok feltérképezésében is segítségünkre lehetnek.
Benoît Mandelbrotnak, a fraktálgeometria atyjának munkássága számos matematikust inspirál mind a mai napig, többek között Bárány Balázst, aki a BME Sztochasztika Tanszékének egyetemi docense és az NKFIH Élvonal Fraktálgeometria és alkalmazásai kutatócsoport vezető kutatója. Balázs már közel két évig kutatott Lengyelországban, másfél évig Angliában és fél évig Izraelben a Hebrew University of Jerusalemen is, ahol a fraktálgeometria egyik meghatározó alakjával, Michael Hochmannal dolgozott együtt. Simon Károllyal és Boris Solomyakkal közös könyve Self-similar and Self-affine Sets and Measures címmel jelent meg az American Mathematical Society kiadásában 2023 decemberében. 2024 júliusában pedig a 9th European Congress of Mathematics konferencia egyik meghívott előadója volt Sevillában. E két kiemelkedő esemény kapcsán beszélgettem vele.

Bárány Balázs (Forrás: Geberle Bertalan, bme.hu)
Mikor, hogyan találkoztál először a fraktálokkal, illetve döntötted el, hogy a fraktálgeometriával szeretnél foglalkozni?
Az már a gimnáziumban világos volt, hogy matematikus szeretnék lenni. Láttam a TV-ben egy ismeretterjesztő műsort a matematikáról. Ebben volt egy beszélgetés egy matematikussal, aki – miközben elmélkedett – naphosszat sétálgatott egy parkban és etette a kacsákat. Gondoltam, hogy hát ezt én is tudnám csinálni.
Feltételezem, hogy nem teljesen így alakult végül…
Nem, nem egészen kacsaetetéssel telnek a napjaim…
Az egyetemen viszonylag korán találkoztam egyszerűbb fraktálokkal, és teljesen lenyűgözött, hogy bármennyire belenagyítunk, ugyanazt látjuk, illetve, hogy valaminek nulla a területe, de végtelen a kerülete. Aztán Simon Károly tanár úr Véletlen fraktálok kurzusa hatalmas lökést adott, hogy ezt a kutatási területet válasszam.
A kurzus során kérted fel témavezetődnek?
Nem teljesen. Ötödéves koromban egyszer vártam a liftre, éppen ő is odaért, és lezajlott életem egyik legfontosabb beszélgetése.
– Balázs, én magáról úgy hallottam, hogy érdeklik a fraktálok.
– Így van, tanár úr, engem nagyon érdekelnek.
– Akkor jöjjön velem!
Vele mentem, és kaptam egy vastag köteg papírt: mindenféle érdekes cikket a fraktálokról. Úgyhogy elég jól sikerült ez a liftre várakozás.
A fraktálokkal való általános ismerkedés során aztán a nemkonformális struktúrájú fraktálok váltak egyre érdekesebbé számomra.
Azaz?
A jól ismert Sierpiński-háromszög esetén például az eredeti, nagy háromszög a saját átskálázott – felére zsugorított – képeiből áll össze.

Sierpiński-háromszög
Amikor nemkonformális a struktúránk, akkor például az egyik irányban az eredeti alakzatot a felére, a másik irányban pedig mondjuk harmadára zsugorítjuk össze. Tehát különböző irányokban, különböző erősségűek lehetnek az összehúzások. Ráadásul lehet nemlineáris is az iterációk során a változás, azaz tud tekeredni, pöndörödni, penderedni. Ez így már nagyon-nagyon meg tudja bonyolítani a kezelhetőséget.
Ugye a fraktáloknál minket elsősorban az érdekel, hogy mekkorák ezek az alakzatok, ahol a nagyság nagyon sokféleképpen érthető: dimenzióként, mint például Haussdorff-dimenzió, vagy box-dimenzió; mértékként, mint Hausdorff- és Lebesgue-mérték stb…
Ha szépen kezelhetők, azaz önhasonlók és a részek diszjunktak (de legalábbis kicsi az átfedésük), akkor a dimenziójuk jól megértett. Egy (általánosan választott) nemkonformális struktúrájú fraktált viszont lényegesen kevésbé értünk – még akkor is, ha a konstruáló függvények lineárisak (ekkor önaffin esetről beszélünk). Michael Hochmannal és Ariel Rapaporttal közösen sikerült kezelnünk az önaffin síkbeli esetet egy 2019-es cikkünkben, és azóta a térbeli esetet is Ariel Rapaportnak, de magasabb dimenziókra egyelőre nincs teljes válaszunk, csak részleges.
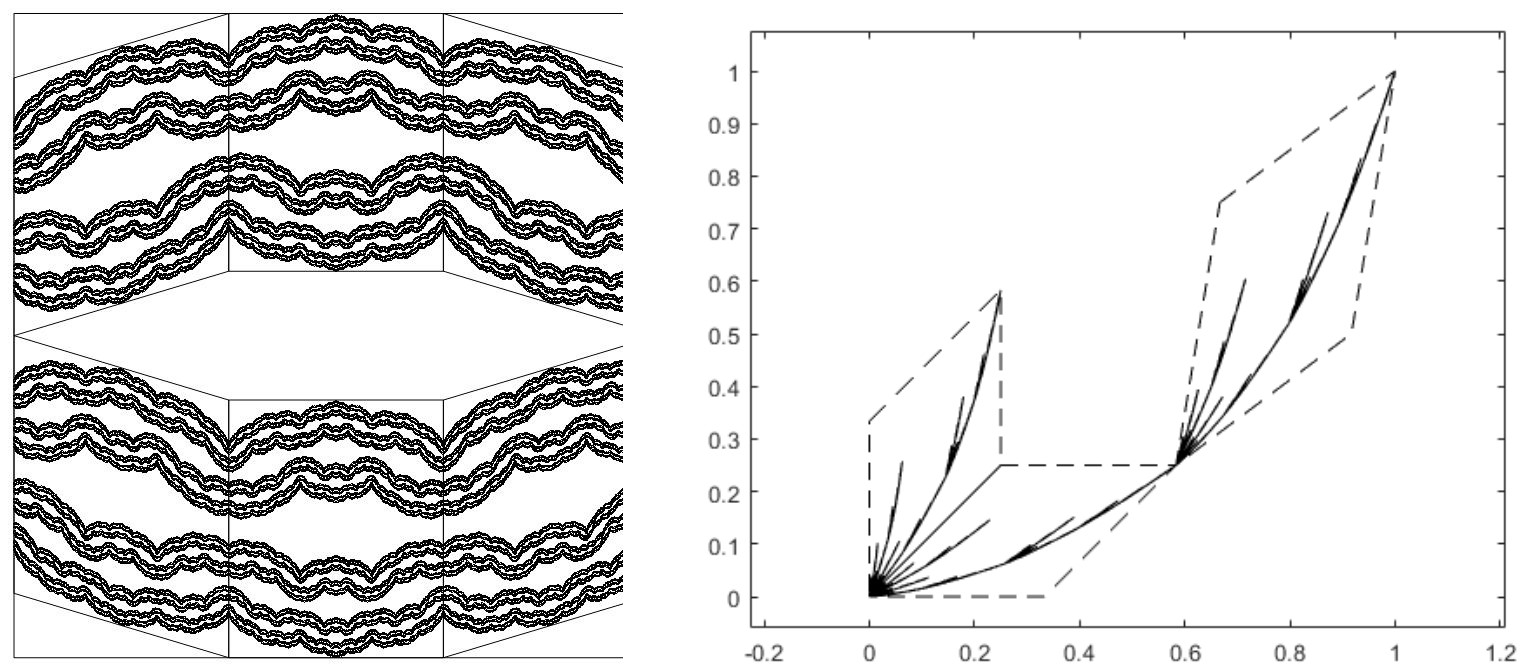
Két önaffin fraktál
Akkor már ezek az eredmények is szerepelnek a tavaly, az AMS Mathematical Surveys and Monographs sorozatában megjelent könyvetekben.
Igen, habár éppen az elmúlt pár évben történt több jelentős áttörés, melyek eredményei, módszerei, alkalmazásai teljes terjedelmükben már nem fértek bele a könyvbe.
Simon Károly és Boris Solomyak jó tizennyolc évvel ezelőtt kezdte el írni a könyvet azzal a céllal, hogy összefoglalják és bemutassák az önhasonló és önaffin rendszerekről szóló ismereteinket. Nyolc évvel ezelőtt tiszteltek meg azzal, hogy bevettek a munkába, hogy felgyorsítsam a folyamatot, ami nem feltétlenül történt meg…
És végül a terület jövőbeli kutatói számára meghatározó alapművet írtatok.
A fejezetek közel fele egyetemi kurzusokon is jól hasznosítható, s jó alapozó/bevezető a témába, de sok „haladó téma” is kifejtésre került, mely inkább a kutatók érdeklődésére adhat számot.

Bárány Balázs és Simon Károly, a könyvükkel a kezükben (Forrás: BME Sztochasztika Tanszék)
Az ECM2024-re meghívott előadóként érkezhettél. Hogyan fogadtad a felkérés hírét, és milyen volt maga a konferencia?
Nagy örömmel, és döbbenettel. Igen nagy megtiszteltetésként éltem meg, hogy meghívást kaptam egy ilyen rangos eseményre, s előadást tarthattam az egyik legkedvesebb témámból. Különösen jól esett a matematikus közösség kedvessége. Sokan odajöttek, hogy pár szót váltsunk egymással, vagy reagáljanak arra, hogy az előadásban elhangzottak kapcsán milyen ötleteik születtek.
Az ilyen megosztások igen gyümölcsözőek szoktak lenni.
Abszolút! Nekem is több cikkem született úgy, hogy odamentem az előadóhoz, naivan megkérdeztem, hogy működhet-e, amire gondoltam, és bizony volt, hogy működött. És viszont: nemrég Domokos Gábor (a Gömböc egyik feltalálója) és diákja, Szesztay Ágoston – akik kövek kopásának modellezésével foglalkoztak – kerestek meg lényegében ismeretlenül, mert a modell vizsgálata során fraktálszerű mintázatokat ismertek fel. A közösen írt cikkünkről nemrég kaptunk igen pozitív bírálatot.
Egy ilyen intenzív időszak után pihenéssel telnek most a napjaid? Illetve mire inspirálnak ezek a sikerek, melyek most a legfontosabb céljaid?
Most nem jellemző a pihenés. Az Erdős Center idén őszi, fraktálokról és hiperbolikus dinamikai rendszerekről szóló szemeszterének keretében szervezünk a fraktálokról – Orgoványi Vilmával, Prokaj Dániel Rudolffal és Simon Károllyal közösen – egy nyári iskolát és egy hozzá kapcsolódó intenzív workshopot. A fraktálok és a dinamikai rendszerek kéz a kézben járnak, szorosan összekapcsolódnak.
Nagyon szeretnénk megérteni a nemkonformális nemlineáris struktúrájú fraktálokat, ami a 2027-ig tartó Élvonal – Kutatási Kiválósági Program célja is. Kiváló kutatócsoportunk van, de természetesen ebben az időszakban csatlakozni fognak még hozzánk PhD-hallgatók, postdokok, vendégkutatók. Bízom benne, hogy az új kutatási eredmények mellett a fiatal, hazai, érdeklődő matematikusok számára is komoly szakmai lehetőséget tudunk nyújtani.
Az interjút Paulovics Zoltán készítette.











