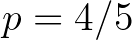Tíz éve halt meg Benoît Mandelbrot, a fraktálgeometria atyja

Benoît Mandelbrot 1924-ben Varsóban született és 2010. október 14-én halt meg Cambridge-ben (Massachusetts, USA). A fraktálgeometria megteremtője volt. Sokat elárul róla önéletírásának [8] címe: The Fractalist: Memoir of a Scientific Maverick (A fraktalista: egy a maga útját járó tudós önéletírása). Zsidó származása miatt 1936-ban, tizenegy éves korában családjával a náci terjeszkedés elől Párizsba menekül. Apai nagybátyja a matematikaprofesszor Szolem Mandelbrojt már 1920 óta élt Franciaországban, doktorátusát Jacques Hadamard témavezetésével szerezte és tanítványai között olyan kiváló matematikusok szerepeltek, mint Paul Malliavin, Jean-Pierre Kahane és Yitzhak Katznelson. A nagybácsi igen nagy hatással volt Mandelbrot fejlődésére, matematikussá válására. Az pedig, hogy segítette Mandelbrot szüleit mint gazdasági és politikai menekülteket megtelepedni Franciaországban, megmentette az életüket. A második világháború idején a német megszállás alatt nem maradhattak Párizsban, délebbre Tulle-be menekültek. A világháború végén, 1944-ben tértek vissza Párizsba.

Előbb a lyoni Lycée du Parc hallgatója, majd a nagyhírű elitképző párizsi École Polytechnique-re jár. Mesterszakos diplomáját az Egyesült Államokban a California Institute of Technology-n szerzi meg aeronautikából. Doktori (Ph.D.) fokozatát matematikából a Párizsi Egyetemen (Sorbonne) kapta 1952-ben. 1955-ben feleségül vette Aliette Kagant, és előbb Genfbe költözött, kicsit később pedig a Lille-i Egyetemen dolgozott. 1958-ban nyári munkát vállalt az IBM-nél. A nyári munkából 35 évig tartó együttműködés lett. Az IBM-nél hozzájutott ahhoz a számítógépes kapacitáshoz, ami végülis lehetővé tette, hogy a fraktálgeometria atyjává váljon. Az IBM Thomas J. Watson Research Centerben 1980 március elsején elsőnek pillanthatta meg számítógépes képen azt a halmazt, amit később Adrien Douady a tiszteletére Mandelbrot-halmaznak nevezett el.

Mandelbrotot a tiszta elméleti kutatások helyett az alkalmazottabb területek érdekelték. A magát egy szűkebb területen beásó kutató helyett polihisztor volt. Kutatásai számos tudományterülethez kapcsolódtak, például a statisztikus fizikához, meteorológiához, közgazdaságtanhoz, orvostudományhoz, turbulens áramlások elméletéhez, mérnöki tudományokhoz, káoszelmélethez...

A matematikában gyakran és előszeretettel tanulmányozott sima függvények, felüleletek helyett a durva, egyenetlen és kaotikus dolgok érdekelték, hiszen a valóságban is inkább ezeket látjuk. Legyen szó egy magashegyi tájról, a Hold felszínéről, egy brokkoliról, egy vadul kanyargó folyóról, a tüdő vagy az agy felszínéről, a BUX, vagy a Dow Jones index alakulását leíró görbéről, vagy mondjuk Norvégia partvonaláról. A fraktál szó az ő alkotása volt a latin frāctus = törött, tört szóból. Általában a matematikában precíz definíciókhoz szokott az ember, azonban egy tudományág, melyet egy Mandelbrothoz hasonló „nyughatatlan” tudós indított útjára, kivétel. Tíz évvel ezelőtt, pár nappal Mandelbrot halála után az origo egyik újságírója felhívta az egyetemünket és néhány átkapcsolás után nekem kellett beszélni vele Mandelbrotról és a fraktálokról. Arra kért, hogy pár mondatban foglaljam neki össze Mandelbrot munkásságát, meg még azt is, hogy mi a fraktálgeometria. Ezután egy meglehetősen szórakoztató párbeszéd következett, hiszen a matematika tudománynépszerűsítésében éppen az a nehéz, hogy sok fogalmat csak több éves tanulmányok után lehet megérteni. Ráadásul a fraktálok esetében még ott van a fogalom precíz definíciója körüli bizonytalanság is. Mindenesetre az origo akkori cikke [14] még most is fenn van az interneten. Hivatalosan, az angol nyelvű wikipédia [12] szerint: „In mathematics, a fractal is a self-similar subset of Euclidean space whose fractal dimension strictly exceeds its topological dimension.” Így az origo újságírója azt kérdezte tőlem, hogy akkor ugye a fraktálok önhasonló halmazok, amire persze az volt a válaszom, hogy gyakran azok, de nem mindig. Például e cikkben később említem és ábrákkal is illusztrálom a véletlen/sztochasztikus folyamat segítségével definiált Mandelbrot-/fraktálperkoláció során előálló halmazokat, amelyek pont a véletlen folyamat eredményeképpen nem lesznek önhasonlóak (legfeljebb csak sztochasztikus értelemben). A következő, a fraktálok elnevezése által sugallt definíció az lehetne, hogy olyan halmaz, mely tört-, azaz nem egész dimenziós. Persze vannak egész dimenziós halmazok, amelyeket a matematikusok szeretnek fraktálnak tekinteni, például a 2. ábra jobb oldalán van egy ilyen alakzat, pontosabban ezen fraktál konstrukciójának negyedik lépésénél kapott ábra. Ennek készítéséről később még írok.

Szórakoztató azt olvasni [12], hogy Mandelbrot szerint hogy módosult a fraktál definíciója: először „gyönyörű, átkozottul kemény, egyre hasznosabb. Ez a fraktál”. Később jött az 1982-es hivatalosabb, korábban már idézett „olyan halmaz, amelynek Hausdorff-Besicovitch dimenziója szigorúan nagyobb, mint a topológiai dimenziója”. Később ezt a definíciót túl szorosnak tartotta, így a következő általánosabb (de a matematikai precizitástól távolabb eső) „definícióval” állt elő: „egy fraktál olyan alakzat, amely az eredetihez valamilyen módon hasonló darabokból áll”. Még később: „a fraktál fogalmát nem definiáljuk precízen, a fraktáldimenziót valamennyi változatra alkalmazható gyűjtőfogalomként használjuk”.

Mandelbrot Neumann János utolsó posztdok hallgatója volt 1953-54-ben Princetonban. Nem véletlen, hogy a 2003-ban, Neumann születésének 100-ik évfordulóján Budapesten tartott VIII. Országos (centenáriumi) Neumann Kongresszuson részt vett. A mellékelt két képet én készítettem a Műegyetemen tartott előadásán. Ezek közül persze Mandelbrot a Mandelbrot-halmaz előtt az a kép, amit különösen kedvelek bár az előadótermi vetítés miatt Mandelbrot nincs túl jól megvilágítva.

Mi is ez a Mandelbrot-halmaz? Tekintsük a legegyszerűbb leképezéseket a komplex számok fölött. A lineáris leképezések viselkedése túl egyszerű, így másodfokúakat véve vegyük az 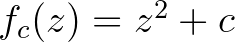leképezéseket, ahol egy tetszőleges rögzített komplex szám. Ha valaki nem szokott komplex számokkal dolgozni, akkor persze 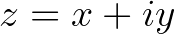, , 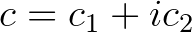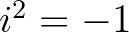helyettesítés után nyugodtan gondolhat az 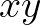-síkon értelmezett 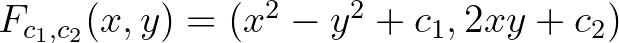leképezésre is. Diszkrét dinamikus rendszerek elméletében arra vagyunk kiváncsiak, hogy egy rögzített transzformáció, függvény ismételt alkalmazása során mi történik. Azaz, ha veszünk egy rögzített 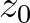kiinduló pontot, akkor azt szeretnénk tudni, hogy a 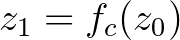, , 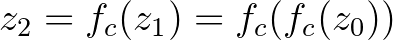..., 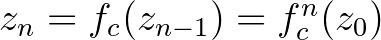, ... sorozat, a 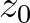pont pályája/orbitja hosszú távon, hogyan viselkedik. A Mandelbrot-halmaz konstrukciója során 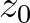-t 0-nak választjuk, és azt vizsgáljuk, hogy egy adott 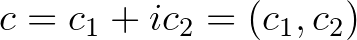értékre az 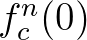, 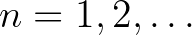pálya korlátos-e. Pl. könnyen látható, hogy ha 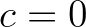, akkor 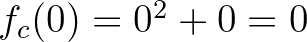, azaz a 0 a rendszer fixpontja, így 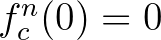, minden 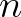-re, tehát a 0 pont pályája korlátos. Azt sem nehéz belátni, hogy ha mondjuk 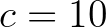, akkor , , 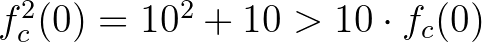és általában 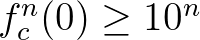, azaz az 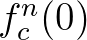pálya nem korlátos, a 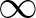-hez tart.

A Mandelbrot-halmaz azon paraméterértékek halmaza, amelyekre az 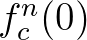, 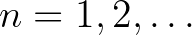sorozat korlátos. Ezen paraméterértékeknek megfelelő képpontok a 4. ábrán a fekete „tócsa” pontjai. A szép színes ábra többi részletéhez egy kis magyarázatra van szükség. Több programmal is tanulmányozhatjuk a Mandelbrot-halmazt, annak részleteit és más fraktálokat is. E cikk készítése közben én a Fractint, illetve a Chaospro programokat használtam. E programokat rövid Google-keresés után bárki letöltheti, és saját maga is felfedezheti a Mandelbrot-halmaz és a fraktálok csodálatos világát. A Mandelbrot-halmaz szokásos ábrázolása során, pl. a 4. ábra rajzolása közben az általam használt Fractint egy referenciakört tekint, ami az ábra készítése közben 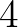sugarú volt, ezután a képpontokat aszerint színezi, hogy mi az a legkisebb 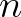érték, melyre 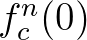már nem tartozik e kör belsejéhez. 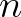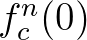A referenciakör sugarát olyan nagyra szokás választani, hogy ha egy paraméterértékre és -re már nem tartozik hozzá, akkor ebből következik, hogy 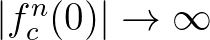. A 4. ábrán pl. a nagy zöld krumpli pontjainak megfelelő értékekre a második, a belsejében levő világoskék zóna pontjai esetében pedig a harmadik iterálásnál kerül ki 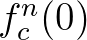a referenciakörből. A színezési mód változtatásával persze más és más „művészi hatás” érhető el. A következő 5. ábrán egy nagyítási sorozatot látunk, azaz az egymást követő képek az előző kép egy kis részletének továbbnagyításával keletkeztek. A Mandelbrot-halmaz már átlagos számítógépek és programok mellett is lélegzetelállító módon nagyítható. Az 5. ábra jobb alsó sarkában levő kép kb. 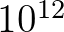-szeres nagyításnak felel meg, ami azt jelenti, hogy ha a kiindulási Mandelbrot-halmazt 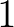méteresnek vesszük, akkor a kinagyított részlet egy hidrogénatom átmérője körüli. Ez persze eltörpül a profi Mandelbrot-zoomolók teljesítménye mellett youtube videókban [4]-ben 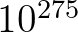-szörös, [7]-ben pedig 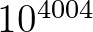-szeres nagyítási mélységig pillanthatunk bele a Mandelbrot-halmazba. A valós anyagi világunk méreteitől messze elszakadnak ezek a nagyítási nagyságrendek, valószínűleg a fizika sohase jut le a 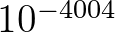méteres tartományba.

Nem kívánok versenyezni a 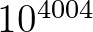-szeres nagyítást elérő szuper videoklipekkel, de azért lejátszható a következő, a Mandelbrot-halmaz részleteire ráközelítő Chaosproval készített saját készítésű kis videoklip:

Itt pedig egy másik, kicsit hosszabb következik, ennek a végén az utolsó nagyítási képnél az adott szinten megállva a számítógép változtatja a színezést, azaz másképp színezi a paraméternek megfelelő képernyőpontokat annak függvényében, hogy hanyadik iteráltra jut ki a referenciakörből :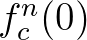

A következő ábrán, nem egy nagyítási sorozatból, még néhány további Mandelbrot-halmaz részlet tekinthető meg.

A Mandelbrot-halmaz komplex dinamikus rendszerekhez kapcsolódik. Azonban Mandelbrot matematikai munkássága nem erre a területre koncentrálódott. A Mathematical Reviews/Mathscinet adatbázisban 143 publikációja szerepel, amelyekre 2102 szerző 2020-szor hivatkozott. Számos területen publikált. Legtöbb publikációja és legtöbbet hivatkozott publikációi is a valószínűségszámítás és sztochasztikus folyamatok területéről kerültek ki. Legtöbbet, 593-szor hivatkozott cikke [9] is ide tartozik és fraktál/tört Brown-mozgással foglalkozik, ami a közönséges Brown-mozgás általánosítása. Egydimenziós esetben a közönséges Brown-mozgás/Wiener-folyamat véletlen bolyongásból kapható meg határátmenettel. A 7. ábrán néhány ilyen számítógéppel generált görbe látható. A bal oldalon egy, a jobb oldalon négy darab, közös koordinátarendszerben. A számítógép az illusztrációk készítése közben véletlen bolyongásokkal közelíti az ábrázolni kívánt Brown-mozgást.

Az ábrákon is látszik, hogy Mandelbrot érdeklődési területének megfelelően egyenetlen/irreguláris fraktálgrafikonok keletkeznek a Wiener-folyamat során. Megmutatható, hogy a Wiener-folyamat Hausdorff-dimenziója egy valószínűséggel 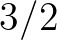, míg a középiskolában megszokott sima függvények, pl. grafikonjának dimenziója 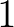. A fenti görbék, bár szabálytalanok, de nem tűnnek túlságosan szokatlannak, hiszen pl. újságokban, hírportálokon is gyakran láthatunk hasonló, szabálytalan grafikonokat, elegendő például csak a tőzsdei árfolyamgörbékre gondolni. Valóban a Python/Sage program [13], amivel ezeket az ábrákat készítettem, egyébként hajlandó részvényárfolyam-görbék sztochasztikus folyamatokon alapuló szimulációjára is. Ezzel el is érkeztünk Mandelbrot tudományos tevékenységének másik nagy területére. Harmadik legtöbbet hivatkozott műve [11] fraktálok, fraktálgeometria pénzügyi folyamatokra való alkalmazásával foglalkozik. Illusztrációként álljanak itt a 8. ábrán BUX, illetve a BUX, Dow Jones, Dax egymás mellett (forrás: [1]):

Valóban hasonlítanak a Brown-mozgás/Wiener-folyamat illusztrálására szolgáló folytonos görbékhez, bár a 2020 márciusában a COVID-19 hatására történő „beszakadást” nem látunk a véletlen görbéken.

Sztochasztikus folyamatokkal nem biztos, hogy e cikk minden olvasója foglalkozott így illusztrációként most szeretnék néhány szót szólni a Mandelbrot-/fraktálperkolációról. Ezt a folyamatot Mandelbrot 1974-ben turbulencia vizsgálatával kapcsolatban [10] vezette be kanonikus megdermesztés (canonical curdling) néven, a Mandelbrot- vagy fraktálperkoláció nevet később kapta a folyamat.

A következő bekezdésben fogok rátérni a véletlen eljárásra. Álljon itt tehát egy determinisztikus módon kapott egydimenziós fraktál, amit már korábban is emlegettem. Vegyük a zárt egységnégyzetet és ezután osszuk fel 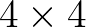egyforma résznégyzetre, és a 9. ábra bal felső sarkában levő képnek megfelelően dobjunk el 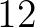db (fehér) kis négyzetet és tartsunk meg 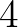db (fekete) négyzetet. Az eljárást ismételgessük mindegyik fekete utódnégyzetben (jobb felső ábra), majd azok utódnégyzeteiben stb., stb. Az egymásba skatulyázott zárt fekete halmazok metszeteként kapjuk a kívánt fraktált, mely egydimenziós lesz, bár a matematikusok általában egyetértenek abban, hogy fraktálnak tekintendő.

A fraktál/Mandelbrot-perkoláció definíciójánál ismét induljunk a zárt egységnégyzetből és ezúttal mondjuk 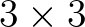egyforma résznégyzetre osszuk fel. Ezután viszont minden egyes kis résznégyzetről „független kockadobásokkal” döntsük el, hogy megtartjuk-e, avagy nem, azaz valamilyen rögzített 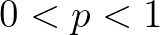-re 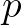valószínűséggel tartsuk meg (fekete) és 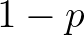valószínűséggel dobjuk el (fehér). Utána az első szinten kapott fekete utódnégyzetekben folytassuk az eljárást. Illusztrációképpen a következő három ábrán láthatunk egy-egy általam készített szimulációt 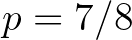, 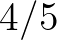és 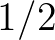értékek esetén. Persze az ilyen véletlen ábrák minden egyes futtatásnál másként néznek ki. Például előállhat az is, hogy már az első körben mondjuk az előző 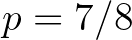esetben az összes utód 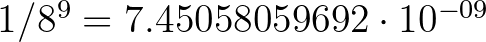valószínűséggel fehér lesz, azaz nem nulla valószínűséggel a fekete halmaz üres lesz.

Fraktálperkolációval kapcsolatban még számos megoldatlan probléma létezik. Talán leghíresebb a következő kérdés. Jelölje 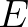a fekete halmazok metszetét. J. T. Chayes, L. Chayes és R. Durrett [3] megmutatta, hogy van egy kritikus valószínűség 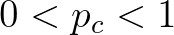, melyre ha 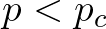, akkor egy valószínűséggel 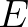teljesen széteső, nincsenek benne összefüggő darabok, ilyen halmaz látható a 11. ábrán. Míg ha 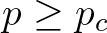, akkor pozitív valószínűséggel a kiindulási egységnégyzet két szemközti oldalát 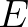egy összefüggő komponense összeköti, ilyen pl. a 10. ábrán látott fraktál. Ennek Hausdorff-dimenziója Kahane és Peyrière [6] egy tétele alapján 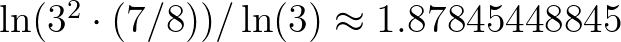. A kritikus 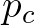valószínűségre vannak becslések, de pontos értéke nem ismert.

Mandelbrot számos kitüntetésben és elismerésben részesült, többek között 1993-ban megkapta a Wolf-díjat (fizikából), 2003-ban a Japán díjat és 2006-ban a Francia becsületrend tiszti fokozatát. Nehéz pontosan megmondani, hogy egy litván származású család, Varsóban született és gyerekeskedő, majd Franciaországban tanuló és dolgozó, később USA-ban letelepedő, francia-amerikai kettős állampolgár gyermeke pontosan melyik nemzet büszkesége lehet. Önéletírása alapján úgy tűnik, nem bánta meg, hogy végülis az IBM-et és az Egyesült Államokat választotta. Érdeklődési területeinek, nyughatatlan, több tudományterületet érintő kutatásainak az IBM által nyújtott kutatási szabadság és rugalmasság tökéletesen megfelelt. Az IBM-nél betöltött „főállása” mellett számos egyetemen (pl. MIT, Harvard) volt vendégprofesszor. Élete végefelé pedig a Yale egyetemen lett Sterling Professor. Érdekesség, hogy a Harvardon az egyik évben a közgazdasági, a rákövetkezőben pedig a matematika tanszék vendégoktatója.

Francia kollégái közül sokat ismerek személyesen, tíz évvel ezelőtt pár nappal halála után hivatalos úton Párizsban jártam és találkoztam, beszélgettem velük, többek között, a szomorú hír okán, Mandelbrotról is. Úgy tűnik, hogy azért ők is „saját halottjuknak” tekintették. Emlékének a Francia Matematikai Tásulat SMF, Gazette des Mathématiciens folyóirata különszámot [5] szentelt.

Irodalomjegyzék

[1] BUX Index, https://www.teletrader.com/bux-index/index/chart/tts-4611743?ts=1596672000000&culture=hu-HU

[2] R. Brooks and P. Matelski, The dynamics of 2-generator subgroups of PSL(2,C), in Irwin Kra (1 May 1981). Irwin Kra (ed.). Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference (PDF). Bernard Maskit. Princeton University Press. ISBN 0-691-08267-7. https://web.archive.org/web/20190728201429/http://www.math.harvard.edu/archive/118r_spring_05/docs/brooksmatelski.pdf

[3] J. T. Chayes, L. Chayes and R. Durrett, Connectivity Properties of Mandelbrot's Percolation Process, Probab. Th. Rel. Fields 77 (1988), 307–324.

[4] Deepest Mandelbrot Set Zoom Animation ever – a New Record! 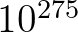(2.1E275 or ), https://www.youtube.com/watch?v=0jGaio87u3A&list=PLVLa3RFibTXVQkK6cv2M74qnKVERD8jqs&index=3&t=0s

[5] S. Jaffard and S. Seuret (szerkesztők), Benoît Mandelbrot, père de la géométrie fractale, Gazette des Mathématiciens, No. 136 (2013).

[6] J.-P. Kahane and J. Peyrière, Sur certaines martingales de Benoit Mandelbrot, Adv. Math. 22 (1976), 131–145.

[7] Mandelbrot Deep Zoom 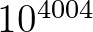, https://www.youtube.com/watch?v=VDMgmZOzZTo&list=PLVLa3RFibTXVQkK6cv2M74qnKVERD8jqs&index=3

[8] B. B. Mandelbrot, The fractalist. Memoir of a scientific maverick. With an afterword by Michael Frame, Pantheon Books, New York, 2012.

[9] B. B. Mandelbrot and J. W. Van Ness, Fractional Brownian motions, fractional noises and applications, SIAM Rev. 10 (1968), 422–437.

[10] B. B. Mandelbrot, Intermittent turbulence in self-similar cascades: divergence of high moments and dimension of the carrier, J. Fluid. Mech. 62 (1974), 331–358.

[11] B. B. Mandelbrot, Fractals and scaling in finance. Discontinuity, concentration, risk, Selecta Volume E. With a foreword by R. E. Gomory. Selected Works of Benoit B. Mandelbrot. Springer-Verlag, New York, 1997.

[12] Wikipedia: Fractal, https://en.wikipedia.org/wiki/Fractal

[13] Tirthajyoti Sarkar, Brownian motion with Python, https://github.com/tirthajyoti/Stats-Maths-with-Python/blob/master/Brownian-motion-with-Python.ipynb

[14] Visnovitz Péter, Büszke bajkeverő volt a káprázatos pacák felfedezője origo.hu 2010.10.23. 23:22 https://www.origo.hu/nagyvilag/20101021-benoit-mandelbrot-matematikus-a-fraktal-atyja-a-geometria-megujitoja-portre.html