
Életének 93. évében elhunyt Andrásfai Béla, a Műegyetem nyugalmazott docense, a gráfelmélet fáradhatatlan kutatója, oktatója és népszerűsítője.
Középiskolai tanulmányait 1942-ben a budapesti Verbőczy István Gimnáziumban (ma Petőfi Sándor Gimnázium) kezdte, 1946-tól a szombathelyi premontrei, majd a Nagy Lajos gimnáziumban folytatta, ahol 1951-ben érettségizett. 1954-ben matematika-fizika szakos tanári diplomát szerzett a budapesti Pedagógiai Főiskolán, majd 1957-ben az Eötvös Loránd Tudományegyetemen is. 1953–1955 között tanársegéd volt a Pedagógiai Főiskola Matematika Tanszékén. Ezt a tanszéket 1947-ben Péter Rózsa (1905–1977) szervezte meg és ő volt a vezetője is, egészen a Főiskola 1955-ben történt megszüntetéséig. Péter Rózsa egészen haláláig megkülönböztetett figyelemmel kísérte Andrásfai Béla munkásságát, mintegy fogadott fiaként szerette.
1955-től egészen 1996-os nyugdíjazásáig a Budapesti Műszaki Egyetem Villamosmérnöki Karán (1992-től Villamosmérnöki és Informatikai Kar) tanított, egyetemi adjunktus volt 1963-tól, majd docens 1965-től. 1963-ban nyerte el a matematikai tudományok kandidátusa címet – Gallai Tibor aspiránsa volt. Az 1986-ban indult mérnök-informatikus szak Diszkrét matematika anyagának kidolgozója és a tárgy első oktatója volt. Oktató és kutató munkája mellett rendszeresen bridzsezett, gyakran nemzetközi versenyek résztvevőjeként.
Sokat mond oktatói munkájáról, hogy 1979-ben a BME Villamosmérnöki Kar hallgatói a kar kiváló oktatójának választották. Talán érdekes megemlíteni, hogy amikor a villamosmérnök-hallgatók mintegy fél évszázada egy kitüntetést akartak létesíteni a legnépszerűbb oktatóik elismerésére, akkor a sokféle kupa, kehely, serleg elnevezés mintájára a díjat köcsög-díjnak nevezték el – akkor ennek a szónak még nem létezett az a jelentése, amely miatt ma ezt a nevet már nem használnánk. Béla viszont joggal nagyon büszke volt rá, később is lelkesen mondta, hogy ő egy köcsög-díjas matematikus. A díjban a matematika világos, érthető előadásán kívül szerepet játszott jó humora és a hallgatókkal kialakított kiváló kapcsolata is.
Derűs egyéniségét tanárkollégái is tapasztalhatták, többek között a Bolyai János Matematikai Társulat Rátz László Vándorgyűlésein, amelyeknek egy időben rendszeres résztvevője volt. A szakmai programokon kívül mindig jelen volt a közös futballozásokon, énekléseken, ő szerkesztette a Hírharang című magazint. A Társulat életében aktívan részt vett, mintegy 25 évig tagja volt a Választmánynak és 1978–1988 között a Felsőoktatási Bizottságnak is. 1975-ben elnyerte a Bolyai János Matematikai Társulat Beke Manó nagydíját.
Kutatási területe az extremális gráfok elmélete volt, egy korai eredményét Erdős már egy 1962-es cikkében megemlítette. Róla nevezték el az ún. Andrásfai-gráfot. Az n-ik Andrásfai-gráfnak 3n–1 pontja van, helyezzük el ezeket egy kör mentén, majd minden pontot kössünk össze az összes többivel, kivéve a vele (akármelyik irányban) szomszédos n–1 ponttal. Az alábbi ábrán az n=4 esetet szemléltetjük kétféleképp lerajzolva. (Készítette: Wikizoli, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=70694402.)

Jelöljük  -vel egy
-vel egy 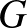 gráfban a független (vagyis páronként nem szomszédos) pontok maximális számát és
gráfban a független (vagyis páronként nem szomszédos) pontok maximális számát és 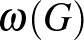 -vel a gráfban található maximális méretű teljes részgráf pontszámát. Ismeretes, hogy minden
-vel a gráfban található maximális méretű teljes részgráf pontszámát. Ismeretes, hogy minden  számpárra van olyan
számpárra van olyan 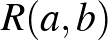 küszöb, hogy minden ennél több pontú
küszöb, hogy minden ennél több pontú 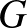 gráfra vagy
gráfra vagy 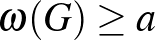 , vagy
, vagy 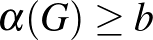 (Ramsey-tétel). Könnyű látni, hogy az Andrásfai-gráf nem tartalmaz három hosszú kört, a komplementere pedig nem tartalmaz
(Ramsey-tétel). Könnyű látni, hogy az Andrásfai-gráf nem tartalmaz három hosszú kört, a komplementere pedig nem tartalmaz 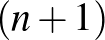 -pontú teljes gráfot, így az
-pontú teljes gráfot, így az 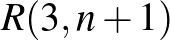 Ramsey-küszöb nagyobb
Ramsey-küszöb nagyobb 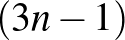 -nél. Ez az alsó becslés egyébként csak
-nél. Ez az alsó becslés egyébként csak 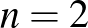 -re és
-re és 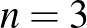 -ra éles.
-ra éles.
Andrásfai egy másik eredménye az ún. 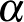 -kritikus gráfokkal foglalkozik (vagyis olyan gráfokkal, amelyek bármely élét elhagyva
-kritikus gráfokkal foglalkozik (vagyis olyan gráfokkal, amelyek bármely élét elhagyva 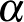 értéke nő). Hajnal András bizonyította be Gallai Tibornak azt a sejtését, hogy egy ilyen, izolált pontokat nem tartalmazó
értéke nő). Hajnal András bizonyította be Gallai Tibornak azt a sejtését, hogy egy ilyen, izolált pontokat nem tartalmazó 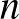 pontú gráfban minden pont foka legfeljebb
pontú gráfban minden pont foka legfeljebb 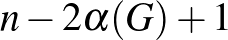 . Jelöljük az
. Jelöljük az 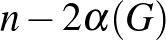 mennyiséget
mennyiséget 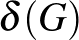 -vel. Ha ez 0, akkor Hajnal tétele szerint az izolált pontokat nem tartalmazó
-vel. Ha ez 0, akkor Hajnal tétele szerint az izolált pontokat nem tartalmazó 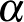 -kritikus gráf minden pontja elsőfokú (vagyis a gráf csak diszjunkt élekből állhat). Ha
-kritikus gráf minden pontja elsőfokú (vagyis a gráf csak diszjunkt élekből állhat). Ha 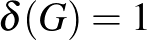 , akkor minden pont foka 1 vagy 2, tehát ha a gráf összefüggő, akkor csak út vagy kör lehet, és könnyű látni, hogy pontosan a páratlan körök lesznek jók. Andrásfai jellemezte a
, akkor minden pont foka 1 vagy 2, tehát ha a gráf összefüggő, akkor csak út vagy kör lehet, és könnyű látni, hogy pontosan a páratlan körök lesznek jók. Andrásfai jellemezte a 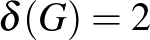 esetet: Ilyenkor pontosan azok az izolált pontokat nem tartalmazó összefüggő gráfok lesznek
esetet: Ilyenkor pontosan azok az izolált pontokat nem tartalmazó összefüggő gráfok lesznek 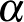 -kritikusak, amelyek a 4 pontú teljes gráfból nyerhetőek úgy, hogy bizonyos éleiket páratlan hosszú úttal helyettesítjük. (A
-kritikusak, amelyek a 4 pontú teljes gráfból nyerhetőek úgy, hogy bizonyos éleiket páratlan hosszú úttal helyettesítjük. (A 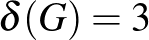 esetre Lovász László és Surányi László adott jellemzést, később Lovász tetszőleges
esetre Lovász László és Surányi László adott jellemzést, később Lovász tetszőleges 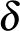 -ra megmutatta, hogy létezik véges sok olyan gráf, amelyekből ezzel a művelettel az összes
-ra megmutatta, hogy létezik véges sok olyan gráf, amelyekből ezzel a művelettel az összes 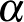 -kritikus gráfot megkaphatjuk.)
-kritikus gráfot megkaphatjuk.)
Egy Erdős Pállal és T. Sós Verával közös cikkben megmutatták, hogy ha egy 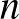 pontú egyszerű gráf kromatikus száma
pontú egyszerű gráf kromatikus száma 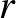 , de a gráf nem tartalmaz teljes
, de a gráf nem tartalmaz teljes 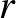 -est, akkor a gráfban van olyan pont, amelynek fokszáma legfeljebb
-est, akkor a gráfban van olyan pont, amelynek fokszáma legfeljebb 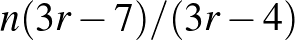 . Erre a cikkre több mint száz másik dolgozat hivatkozott.
. Erre a cikkre több mint száz másik dolgozat hivatkozott.
Különösen jelentős volt a matematikát népszerűsítő tevékenysége. A gráfelméletnek a Műegyetemen nagy hagyományai vannak: Az egész világon a BME volt az első egyetem, ahol önálló gráfelméleti kurzus indult (Kőnig Dénes tartotta az 1930-as években a Műegyetem és a Pázmány diákjainak, hallgatói között volt többek között Erdős Pál, Gallai Tibor, Klein Eszter, Szekeres György, Turán Pál). A második világháború után Egerváry Jenő, Gallai Tibor és rövidebb ideig Hajós György is a Műegyetem oktatói voltak. A műegyetemi villamosmérnök hallgatók kötelező matematika tananyagában azonban a gráfelmélet csak mintegy 30 éve szerepel (számos neves európai műegyetemen még később vezették be). Így több évtizeden át egy személyben Andrásfai jelentette a BME-n „a” gráfelméletet: rendszeresen speciális előadásokat tartott az érdeklődő hallgatóknak és a Mérnöktovábbképző Intézetben. Egyetemi jegyzetei mellett ugyancsak jelentős volt a több kiadást megért „Ismerkedés a gráfelmélettel” című könyve, amelyet főleg érdeklődő gimnazistáknak (és tanáraiknak) szánt. Egyetemi oktatói munkáján kívül ezeknek a könyveknek is köszönhető, hogy a gráfelmélet oktatásának emlékezetes alakjává vált.

Budapesti Műszaki és Gazdaságtudományi Egyetem
Villamosmérnöki és Informatikai Kar
Számítástudományi és Információelméleti Tanszék
Andrásfai Béla műveinek válogatott listája:
(A) Tudományos dolgozatok:
1. Neuer Beweis eines graphentheoretisches Satzes von P. Turán, MTA Mat. Kut. Int. Közleményei, 7 (1962) 193–196.
2. Graphentheoretische Extremalprobleme. Acta Math. Acad. Sci. Hungar. 15 (1964) 413–438.
3. On critical graphs, Theory of Graphs Internat. Symp. Rome 1966, 9–19.
4. On the connection between chromatic number, maximal clique and minimal degree of a graph, Discete Math. 8 (1974) 205–218. (Erdős Pállal és T. Sós Verával közösen)
(B) Tankönyvek és ismeretterjesztő könyvek:
1. Gráfelmélet. Villamosmérnökök számára; Tankönyvkiadó, Bp., 1968 (Mérnöki Továbbképző Intézet kiadványa V.)
2. Ismerkedés a gráfelmélettel, Tankönyvkiadó, Budapest, 1971, 1973, 1984. Angolul: Introductory graph theory, Akadémiai Kiadó, Budapest és Adam Hilger Ltd. Bristol, New York, 1977
3. Gráfelmélet. Folyamok, mátrixok, Akadémiai Kiadó, Budapest, 1983. Angolul: Graph theory. Flows, matrices, Akadémiai Kiadó és Adam Hilger Ltd. Bristol, Philadelphia, 1991
4. Gráfelmélet, Polygon Kiadó, Szeged, 1997
5. Gráfelmélet villamosmérnökök számára, Tankönyvkiadó, Budapest, 1968, 1971
6. Matematikai érdekességek, Gondolat Kiadó, Budapest, 1969 (társszerzőkkel), Németül: Mathematisches Mosaik, Urania Verlag, Leipzig–Jena–Berlin, 1977
7. Vonalak és felületek topológiája, Tankönyvkiadó, Budapest, 1971, Polygon Kiadó, Szeged, 1994
8. Versenymatek gyerekeknek, Tankönyvkiadó, Budapest, 1986, 1988, Calibra Kiadó, 1992, 2002
9. Infor-matek, Polygon Kiadó, Szeged, 1997 (Ablonczy Péterrel)











