Szele Tibor Emlékérem 2023
Kiemelkedő tudományos és utánpótlás-nevelő munkássága alapján a Bolyai János Matematikai Társulat 2023-ban Molnár Lajosnak ítélte a Szele Tibor emlékérmet. A díjat Laczkovich Miklós, a bizottság elnöke adta át.

Molnár Lajos 1964-ben született Kemecsén. A Debreceni Egyetemen szerzett matematikus diplomát (1988), majd PhD fokozatot (1990). 2005-ben lett az MTA doktora. 2007 óta egyetemi tanár. 2015-ben költözött Szegedre, azóta a Szegedi Tudományegyetem Bolyai Intézete Analízis Tanszékének tanszékvezető egyetemi tanára.
Kutatási területe a funkcionálanalízis, az operátorelmélet, illetve a lineáris algebra. Az MTMT szerint 169 tudományos közleménye jelent meg, amelyekre 1907 független hivatkozást kapott. Dolgozatai rendszeresen jelennek meg a fenti területek, valamint a matematikai fizika rangos, vezető folyóirataiban. Szűkebb kutatási témája az úgynevezett megőrzési problémák vizsgálata, amelyek (elsősorban függvények, mátrixok vagy operátorok alkotta) különböző matematikai struktúrák különféle szimmetriáinak a meghatározásával kapcsolatosak. Molnár Lajos alapvető szerepet játszott abban, hogy a korábbi, ún. lineáris megőrzési problémák vizsgálatáról a hangsúly az utóbbi két évtizedben fokozatosan áttevődött a nemlineáris problémákra, és ma egyértelműen ezek jelentik a fő kutatási irányt a területen. Eredményeinek jelentőségére két példa a következő: A Handbook of Quantum Logic and Quantum Structures kézikönyv Wigner Jenő nevezetes, a kvantummechanikai szimmetriatranszformációkról szóló alaptételével kapcsolatos fejezetében több mint két tucat esetben említik, ill. tárgyalják az ezen tétellel és annak különböző kiterjesztéseivel kapcsolatos eredményeit. MTA doktori disszertációját a Springer könyv alakban jelentette meg.
Tudományos tevékenysége elismeréseként 1992-ben Grünwald Géza díjat, 1999-ben Erdős Pál díjat, 2011-ben Akadémiai Díjat kapott. 2012-ben MTA Lendület pályázatot nyert, emellett összesen 20 kutatási pályázatnak volt a vezetője. Elnyerte a Széchenyi Professzori ösztöndíjat, volt Humboldt ösztöndíjas Németországban, distinguished visiting professor az USA-ban. Eredményeiről mintegy 200 tudományos előadást tartott nemzetközi konferenciákon, külföldi egyetemeken és kutatóintézetekben a világ számos pontján Ázsiától Észak-Amerikáig. Vendégkutató volt többek között Franciaországban, Olaszországban, Szlovéniában, Tajvanon, az USA-ban.
Aktív szakmai közéleti tevékenységéből a legfontosabbak: 2014-20 között tagja volt az MTA Doktori Tanácsának, 2016-17-ben az NKFIH Matematika-Számítástudomány szakértői csoportjának volt elnöke. Nyolc nemzetközi folyóirat szerkesztésében vesz részt. 2018-től főszerkesztője a Szegedi Acta folyóiratnak, amelyet nagy munkával sikerült megújítania, és ennek eredményeképpen a folyóirat kiadása a Springer kiadóhoz került.
Molnár Lajos kiemelkedő szerepet vállal az utánpótlás nevelésében, a fiatalok kutatómunkába történő bevonásában. Hét OTDK dolgozatnak volt témavezetője. Ezek közül több országos első díjat nyert, és volt olyan, amelyet az OTDK Pro Scientia Aranyéremmel jutalmazott. Hat, fokozatott szerzett PhD hallgató témavezetője volt. Közülük hárman is elnyerték a Grünwald Géza díjat, és többen is vezető oktatói állást töltenek be magyar, illetve külföldi egyetemeken. Jelenleg két aktív PhD hallgatója van. Ugyan hivatalosan nem voltak doktoranduszai, de Gehér György és Virosztek Dániel tudományos munkáját a kezdetektől évekig segítette és irányította. Gehér György ezen periódusban kapott Grünwald Géza díjat illetve nyerte el a JMAA folyóiratnak az év legjobb cikkét jutalmazó díját. Virosztek Dániel (szintén Grünwald Géza díjas), a Lendület-pályázat nyerteseként került a Rényi Intézetbe.
Grünwald Géza Emlékérem 2023
A Grünwald Géza Emlékérem jogelődjét, a Grünwald Géza Emlékdíjat a Bolyai János Matematikai Társulat 1951-ben alapította a matematikai alapkutatásban kiemelkedő tudományos eredményeket elérő, fiatal magyar matematikusok jutalmazására. 2018-ban a Társulat a jutalmazhatók körét kiterjesztette a Magyarországon tanulmányokat folytatott külföldi kutatókra is. 2023-ban a Grünwald Géza Emlékéremre mindössze egy felterjesztés érkezett: Garamvölgyi Dániel pályázata, melyet a Bizottság, egyhangú döntéssel, támogatásra méltónak talált.
Garamvölgyi Dániel 1995-ben született. Matematikus alap-, majd mesterszakos tanulmányait az Eötvös Loránd Tudományegyetemen végezte el, és 2023-ban az ELTE doktori iskolájában szerzett abszolutóriumot. Jelenleg a HUN-REN-ELTE Egerváry Jenő Kombinatorikus Optimalizálási Kutatócsoportban dolgozik, valamint a Rényi Alfréd Matematikai Kutatóintézet fiatal kutatója.
Garamvölgyi Dániel 6 cikket jegyez színvonalas nemzetközi folyóiratokban, további két publikációja konferenciakötetekben jelent meg, három munkája pedig jelenleg bírálat alatt áll. Kombinatorikai problémákon dolgozik, fő érdeklődési területe a gráfok merevségi tulajdonságainak vizsgálata. A terület alapkérdése a következő: egy adott G gráf csúcsait a d-dimenziós euklideszi térbe leképezve, kongruencia erejéig egyértelműen meghatározzák-e a beágyazást a G éleihez tartozó szakaszok hosszai? Garamvölgyi Dániel, társszerzőivel együtt, a témakör több fontos kérdését vizsgálta: többek között a gráf rekonstruálhatóságát éleinek hosszából, csúcsainak globális összekapcsolódását, illetve a gráf globális merevségének kérdését (utóbbi azt jelenti, hogy a gráf tetszőleges realizációja, kongruencia erejéig, egyértelműen meghatározott az élhosszai által). A kombinatorikus módszereken túl eredményesen alkalmazta az algebrai geometria eszköztárát is, amelyek segítségével mély eredményeket ért el. Az elmúlt időszakban a területen az algebrai geometriai megközelítés egyik fő szakértőjévé vált.
Farkas Gyula Emlékdíj 2023
A matematika alkalmazásával szoros kapcsolatban álló jelentős tudományos eredményeikért Farkas Gyula Emlékdíjban részesült Varga Anita és Tóbiás András. A díjakat Simon Péter, a Bolyai Társulat főtitkára adta át a díjazottaknak.

Varga Anita 1992-ben született. A Budapesti Műszaki és Gazdaságtudományi Egyetemen szerzett 2014-ben matematika BSc, majd 2016-ban alkalmazott matematika MSc diplomát. Az MSc diplomamunkájában az Xpress optimalizáló szoftverhez készített egy új modult, amely az ELTE-n fejlesztett LEMON C++ gráfelméleti könyvtár objektumait és függvényeit teszi elérhetővé az Xpress keretein belül.
Varga Anita az egyetemi évei alatt kezdett el dolgozni a BME Építészmérnöki Karán anyagdepók elhelyezési problémáin és az egyetem elvégzése után még két évig félállású tudományos segédmunkatársként dolgozott itt. Ezen időszak alatt több publikáció is született főként a projekttervezés témakörében.
Mester diplomája megszerzése után, 2016 őszétől folyamatosan tanított a BME Differenciálegyenletek tanszékén. 2022 őszétől teljes állásban dolgozott itt. Doktori fokozatát 2023-ban szerezte a BME Matematika- és Számítástudományok Doktori Iskolájában, ahol a 2020/21 tanévben ÚNKP ösztöndíjas volt.
Varga Anita jelenleg a Budapesti Corvinus Egyetemen félállású tudományos segédmunkatárs és félállású adjunktus. 2023-tól a Corvinus Operációkutatási Kutatócsoport tagja. Érdeklődési területei a lineáris és konvex optimalizálás elmélete, belsőpontos algoritmusok és az operációkutatás ipari, gazdasági alkalmazásai.
A doktori értekezésében általános elemzését adta a belsőpontos algoritmusok egy családjának. Ezek a belsőpontos algoritmusok polinom időben megoldják a lineáris programozási feladatokat, bizonyos speciális lineáris komplementaritási feladatokat (LCP) és általánosíthatóak szemidefinit programozási feladatokra, kúpoptimalizálási feladatokra is.
Kutatásának egyik fő kérdése az volt, hogy az algoritmus során milyen keresési irányok alkalmazásával szavatolható még az elméletben ismert legjobb komplexitás megtartása. Ennek jelentősége például lineáris komplementaritási feladatok megoldásánál lehet. Ugyanis általános esetben az LCP NP-nehéz probléma, így nem reménykedhetünk olyan hatékony algoritmusban, ami mindegyik LCP feladatot meg tudja oldani. A numerikus tesztek azt mutatják, hogy az algoritmus során a keresési irány változtatása lehetővé teheti a nehéz LCP feladatok esetén a „problémás” régiók elkerülését. Az eredményei jó alapot adhatnak egy hibrid algoritmus konstruálása felé, mellyel hatékonyan lehetne általános LCP feladatokat kezelni.
Az elméleti eredmények mellett numerikusan is vizsgálta a kérdéskört: különböző algoritmusokat implementált Matlabban, és számos feladat megoldásán tesztelte a tárgyalt eljárásokat és azok paraméterbeállításait.
A tanítás mellett 3 BSc diák témavezetője volt, illetve közreműködött mérnök és közgazdász hallgatók részére készített matematikai e-tananyagok fejlesztésében.
Az évek során számos alkalmazott projektben is részt vett, mert fontosnak tartja, hogy az elmélet mellett valódi alkalmazásokba is betekintést nyerjen. Foglalkozott villamosenergia-termelés tervezés optimalizációs feladattal, illetve az előző évben tagja volt annak a Koi Tamás vezette csoportnak a BME-n, akik az NKHV Zrt megbízásából hulladékgazdálkodási feladatokon dolgoztak. Ebben a munkában a modellezésért, majd a kapott feladatok számítógépes megvalósításáért volt felelős. 2023 januárjától félállásban dolgozik az EPIC InnoLabs Nonprofit Kft-nél, ahol operációkutatóként tevékenykedik.
Rendszeres résztvevője, előadója nemzetközi konferenciáknak. Aktívan részt vett az Operációkutatási Szeminárium szervezésében a BME-n, jelenleg pedig a Corvinus Egyetemen végez hasonló tevékenységet. 2023 augusztusában a Corvinus Egyetemen került megrendezésre a EUROPT Workshop, melynek szervezőbizottságának aktív helyi tagjaként járult hozzá a rendezvény sikerességéhez.

Tóbiás András 1992-ben született Budapesten. Alapszakos matematika diplomáját a Budapesti Műszaki és Gazdaságtudományi Egyetemen szerezte 2014-ben, míg mesterszakos diplomáját 2016-ban a Technische Universität Berlin-en, szintén matematikából. Ugyanitt szerzett PhD fokozatot 2019-ben Wolfgang König témavezetésével. Ezután három évig szintén a TU Berlin munkatársaként dolgozott Noemi Kurt kutatócsoportjában. 2022 óta Budapesten él, a Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatika Karán, a Számítástudományi és Információelméleti Tanszéken adjunktus, valamint a Rényi Alfréd Matematikai Kutatóintézet részmunkaidős munkatársa.
Tóbiás András fő kutatási eredményeit a populációgenetika matematikai modelljeinek vizsgálatával érte el, többek között a dormancia, logisztikus versengés, horizontális géntranszfer témájában.
Megmutatta, hogy bizonyos sztochasztikus adaptív dinamikai modellekben a dormanciára való képesség (ami az élőlények/sejtek inaktív állapotára utal), szelekciós előnyt ad egy mutáns részpopulációnak, annak ellenére, hogy a mutáns a rezidenshez képest rosszabbul szaporodik. Ezt a jelenséget (versengés által indukált dormancia) az elméleti biológusok is plauzibilisnek tartják, és az eredményeit idézik. A módszertan elágazó folyamatokra és differenciálegyenlet-rendszerek kvalitatív viselkedésére épül. Egy másik kutatásban a dormancia és a horizontális géntranszfer kölcsönhatását vizsgálták. A horizontális géntranszfer bizonyos paraméterválasztások esetén lehetővé teszi rezidens és mutáns koegzisztenciáját.
Egy másik kutatási irány az olyan részecskerrendszereknek a szisztematikus vizsgálata, amelyekre az a jellemző, hogy a részecskék nem egymástól függetlenül, hanem gyakran egyszerre végeznek bizonyos „tevékenységeket" (pl. szaporodás, halálozás, migráció, összeolvadás) Poisson-pontfolyamatok által vezérelve, amit koordinációnak nevezünk. Ennek egyik első példája a Lambda-koaleszcens volt 1999–2000-ben (Pitman, Sagitov), és azóta számos biológiailag releváns példát vizsgáltak. Ezek a folyamatok rendszerint populációgenetikai modellek skálázási limeszeinek (momentum)duálisaként lépnek fel, amit Tóbiás András társszerzőivel igazolt. A részecskerendszer koordinációja ritka, de nagy hatású – a populációnak nagy populációméret esetén is pozitív hányadát érintő –szelekciós/mutációs/migrációs/genetikai sodródásos eseményeknek felel meg a duális folyamatban. Megmutatták azt is, hogy ha nincs összeolvadás a modellben, akkor a folyamat részecskeszámának várható értéke csak a Poisson-pontfolyamatok intenzitási mértékeinek összsúlyától függ, és hasonló módszerekkel becsülték a részecskeszám szórásnégyzetét is.
Legújabban, egy Annals of Probability folyóiratban elfogadott cikkben az adaptív dinamikai inváziómodellek vannak általánosítva kontakt folyamatra. Itt egy nagy tóruszon a kontakt folyamatban bizonyos szaporodási (fertőzési) események során mutáció következik be, ami a szaporodási ráta növekedéséhez vezet. A határértékben megjelenő folyamat érdekessége, hogy a térbeliség fontos szerepet játszik benne: a mutáns túlélési esélyénél számít például, hogy hány fertőzött szomszédja volt, amikor született.
A populációgenetikai modelleken kívül Tóbiás András általános véletlen intenzitású Poisson-pontfolyamatok perkolációjáról is több cikket írt, amelyek eredményeit a mobil-hálózatok összefüggőségi tulajdonságainak elméletében széleskörűen használják.
Tóbiás András 16 cikk, három könyvrészlet és egy konferenciaközlemény szerzője. Publikációi többek között a valószínűségelmélet vezető folyóirataiban, az Annals of Probability, Stochastic Processes and Their Applications, Electronic Journal of Probability folyóiratokban jelentek meg. Szemináriumi előadásokat és konferenciaelőadásokat tartott többek között Freiburgban, Bielefeldben, Bochumban, Bath-ban és Bécsben. A Berlinben töltött évek alatt több PhD-diákoknak szóló szeminárium és egyéb rendezvény szervezője volt.
Rényi Kató Emlékdíj 2023
2023-ban a Bolyai János Matematikai Társulat négy jelöltnek ítélte oda a Rényi Kató Emlékdíjat, melyből Kocsis Anett és Nagy Kinga a díj I. fokozatában, Batta Gergely és Komálovics Ábel pedig a díj II. fokozatában részesült.
A továbbiakban bemutatjuk a díjak indoklását, de szeretnénk hozzátenni, hogy mindegyik jelöltről elmondható, hogy a kutatás mellett aktívan részt vesznek oktatási tevékenységben vagy tudományos versenyeken, mint az OTDK, emellett a tudományos közösségért is aktívan tesznek. Az indoklások csak betekintést nyújtanak a kitüntetettek eddigi munkásságába, amelyhez a Rényi Kató Emlékdíj bizottság (Pete Gábor megbízott elnök, Kiss Gergő titkár) további sok sikert kíván.

Kocsis Anett az Eötvös Loránd Tudományegyetem elsőéves MSc hallgatójaként kiemelkedő teljesítményt nyújtott. Már BSc hallgatóként aktív és érdemi kutatói tevékenységet folytatott a matematika több különböző területén. Eleddig 6 cikket nyújtott be, különböző társszerzőkkel, melyből 2 már meg is jelent a Discrete Mathematics illetve az Acta Arithmetica folyóiratokban.
Eddigi kutatásaiból három témát lehet kiemelni. Egyrészt a kombinatorikus számelméleti eredményeket, melyek Matolcsi Dáviddal, Sándor Csabával és Tőkős Györggyel közösek. Ebben multiplikatív bázisok méretére adnak aszimptotikus eredményeket. (Például, milyen sűrű lehet a pozitív egészek egy olyan halmaza, hogy két ilyen szám szorzataként bármilyen pozitív egész előáll?)
A második, jóval komplexebb projekt témavezetőjével, Elekes Mártonnal, valamint Kátay Tamással, Pálfy Mátéval és más jeles kutatókkal közösen valósult meg, melynek egy reprezentatív kérdése: Hogyan néz ki egy Baire-kategória értelemben tipikus Abel-csoport?
A csak a BSc szakdolgozatában leírt újabb kutatásai, szintén az előbb említett kutatócsoporttal közösen, azt a leíró halmazelméleti problémakkört vizsgálják, hogy általános lengyel terekben a különböző értelemben vett kicsinység tulajdonságok (mint pld Haar-null és Haar-első kategória) milyen számosság típusú következményekkel járnak (uniformitás, fedési szám, kofinalitás, Erdős-Sierpinski-jellegű eredmények).

Nagy Kinga a Szegedi Tudományegyetem Bolyai Intézetének II. éves MSc hallgatója. Már első évesként aktív kutatásba kezdett Vígh Viktor témavezetése mellett. Ez eddig 3 geometriai tartalmú kéziratban jelent meg, melyből az egyiket a Discrete Mathematics, míg egy másikat a Discrete and Computational Geometry folyóirat közölt, mindkettő Q1-es lap.
Az előbbiben azt a természetes kérdést válaszolták meg, hogy hogyan nézhetnek ki a körlap legfeljebb három részre bontásai (a határtól eltekintve) egybevágó részekre, melyek határa szakaszonként sima. Ez a karakterizációs eredmény egy többlépcsős folyamat eredménye, mely Kurusa, Lángi és Vígh korábbi munkájára épül.
Második cikkükben aszimptotikus eredményeket bizonyítottak azon kérdésre, hogy ha adott egy konvex síkidom L, akkor milyen jól lehet közelíteni egy sima határú konvex síktartományt úgynevezett L-konvex poligonokkal.
Harmadik cikkükben szférikus halmazok véletlen konvex közelítéseit vizsgálták, különböző szférikus konvexitás fogalmak közötti folytonos átmeneteket definiálva.

Batta Gergő a Debreceni Egyetem Matematika- és Számítástudományok Doktori Iskolájának elsőéves doktorandusz hallgatója. Korán bekapcsolódott a Debreceni Egyetem egyik nagy témakörében folyó kutatásba, melyet Győry Kálmán és az egyetem Algebra és Számelmélet tanszéke fémjelez.
Szikszai Márton témavezetése mellett diofantoszi típusú halmazokat vizsgált, ahol a halmaz elemei olyanok, hogy bármely kettő szorzatához 1-et adva egy egész szám magasabb rendű hatványát kapjuk. Azon esetről, amikor a hatványok négyzetszámok, sok ismerettel rendelkezünk, ám az általános eset még erősen nyitott. Ezen halmazok vizsgáltatát terjesztették ki arra az esetre, ha a halmaz elemei racionális számok. Ezen belül is 3 és 4 pontú racionális diofantikus halmazok körében értek el számottevő eredményeket és találtak új konfigurációkat. Jelenleg Hajdu Lajos témavezetésével a diofantikus halmazok gráfelméleti vonatkozásait vizsgálja.

Komálovics Ábel jelenleg Szegedi Tudományegyetem Matematikai Doktori Iskola elsőéves PhD hallgatója; egyetemi tanulmányait a Budapesti Műszaki Egyetemen végezte Molnár Lajos témavezetése mellett. A közös munka eredményeként 1 cikkük jelent meg a Q1-es Journal of Mathematical Analysis and Applications folyóiratban.
Cikkükben C*-algebrák pozitív kúpjain bevezetett olyan távolság fogalmakat vizsgáltak, mint a Bures- és Hellinger-metrikák, amelyek fontos szerephez jutnak a kvantuminformáció-elméletében is. Ezen speciális metrikák hasonló tulajdonságai mentén indulva távolságmértékeknek egy egy-paraméteres családját vezették be, felölelve a fenti eseteket is. Ezen család létezésével, pozitivitásával és alapvető tulajdonságaival foglalkozik a fenti munka. A cikk eszköztára a funkcionálanalízis széles tárházából merít, olyan kurrens fogalmakat is alkalmazva, mint a „Kadison transitivity” vagy a C*-algabrák nyom-szerű lineáris operátorainak elmélete. A dolgozat szisztematikusan kitér a Hilbert-tér esetére is, ami a kvantuminformáció-elméletben különösen fontos.
Jelentés a 2023. évi Kürschák József Matematikai Tanulóversenyről
A Bolyai János Matematikai Társulat a 2023. évi Kürschák József Matematikai Tanulóversenyt október 6-án, közép-európai idő szerint 14 órai kezdettel rendezte meg a következő tizenkét helyszínen: Budapest, Cambridge, Debrecen, Kaposvár, Kecskemét, Miskolc, Nyíregyháza, Pécs, Szeged, Székesfehérvár, Tatabánya és Zalaegerszeg.
A Társulat elnöksége a verseny lebonyolítására az alábbi bizottságot kérte fel: Biró András, Fleiner Tamás (elnök), Frenkel Péter, Harangi Viktor, Kós Géza, Kovács Benedek, Maga Péter, Pach Péter Pál és Tóth Géza. A bizottság szeptember 20-i ülésén a következő feladatokat tűzte ki:
1. Legyen 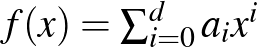 , ahol
, ahol 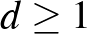 , az
, az 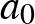 , ...,
, ..., 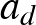 együtthatók nemnegatív egészek,
együtthatók nemnegatív egészek, 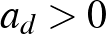 . Igazoljuk, hogy végtelen sok olyan
. Igazoljuk, hogy végtelen sok olyan 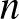 pozitív egész szám van, amelyre
pozitív egész szám van, amelyre 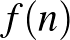 az
az 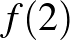 ,
, 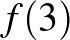 , ...,
, ..., 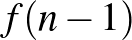 számok egyikével sem osztható.
számok egyikével sem osztható.
2. Legyen 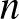 pozitív egész szám. Nevezzük csúcsnak a síkbeli derékszögű koordinátarendszer azon pontjait, amelyeknek mindkét koordinátája az
pozitív egész szám. Nevezzük csúcsnak a síkbeli derékszögű koordinátarendszer azon pontjait, amelyeknek mindkét koordinátája az 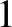 ,
, 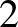 , ...,
, ..., 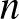 számok közül kerül ki. Nevezzük élnek azon egységnyi hosszúságú szakaszokat, amelyeknek mindkét végpontja csúcs. Néhány élt pirosra színeztünk úgy, hogy bármely két különböző csúcs között pontosan egy piros töröttvonal vezessen. Az
számok közül kerül ki. Nevezzük élnek azon egységnyi hosszúságú szakaszokat, amelyeknek mindkét végpontja csúcs. Néhány élt pirosra színeztünk úgy, hogy bármely két különböző csúcs között pontosan egy piros töröttvonal vezessen. Az 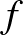 piros él fontos az
piros él fontos az 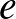 él számára, ha az
él számára, ha az 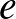 két végpontját összekötő piros töröttvonal áthalad
két végpontját összekötő piros töröttvonal áthalad 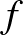 -en. Bizonyítandó, hogy van olyan piros él, amely legalább
-en. Bizonyítandó, hogy van olyan piros él, amely legalább 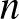 él számára fontos.
él számára fontos.
3. Adott egy  konvex húrötszög és egy belső
konvex húrötszög és egy belső 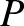 pontja úgy, hogy
pontja úgy, hogy 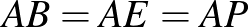 és
és 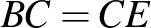 . Az
. Az 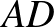 és
és 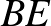 egyenesek metszéspontja
egyenesek metszéspontja 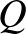 . Az
. Az 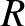 és
és 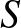 pontok a
pontok a 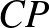 , illetve a
, illetve a 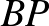 szakaszokon fekszenek úgy hogy
szakaszokon fekszenek úgy hogy 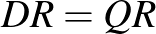 és
és 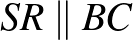 . Mutassuk meg, hogy a
. Mutassuk meg, hogy a 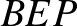 és
és 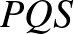 körök érintik egymást.
körök érintik egymást.
A bizottság a beérkezett dolgozatok átnézése után, december 6-i ülésén a következő jelentést fogadta el:
„A verseny minden helyszínen rendben zajlott le, 116 regisztrált versenyzőtől összesen 90 dolgozat érkezett be.
Az idei versenyen 14-en oldották meg esetleg kisebb hiányossággal az első feladatot. A második feladat esetén 7-en értek el hasonló eredményt, és további 8 versenyzőnek van értékelhető részeredménye. A harmadik feladat bizonyult a legnehezebbnek: erre mindössze egyetlenegy helyes megoldás érkezett, további két versenyző pedig jó irányba indult, de elakadt.
Egy versenyző helyesen oldotta meg az első és a harmadik feladatot, a másodikra adott megoldása pedig lényegében helyes. Ezért
I. díjat és 60000 Ft pénzjutalmat nyer
Molnár-Szabó Vilmos, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója (tanárai Dobos Sándor, Fazakas Tünde, Ádám Réka, Hujter Bálint, Bán-Szabó Áron, Szűcs Gábor, Fey Dávid és Seres-Szabó Márton).
Két versenyző oldotta meg helyesen az első két feladatot. Ezért a teljesítményért
II. díjban és 30000 Ft pénzjutalomban részesül
Móricz Benjamin, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója (tanárai Dobos Sándor, Fazakas Tünde, Ádám Réka és Hujter Bálint) és
Szakács Ábel, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 10. osztályos tanulója (tanárai Hujter Bálint, Kiss Géza és Terpai Tamás).
Egy versenyző az első feladat helyes megoldása mellett javítható hibától eltekintve megoldotta a második feladatot is. Ennek megfelelően
III. díjat és 20000 Ft pénzjutalmat kap
Varga Boldizsár, a Békásmegyeri Veres Péter Gimnázium 11. osztályos tanulója (tanára Holló Gábor).
Egy versenyző megoldotta az első feladatot, és a második feladatra olyan javítható megoldást adott, amiből lényeges elemek hiányoznak. Ez alapján
1. dicsérettel és 10000 Ft pénzjutalommal díjazzuk
Czanik Pált, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulóját (tanárai Lenger Dániel és Kocsis Szilveszter).
Végül három versenyző az első feladatra adott helyes megoldás mellett érdemi részeredményt ért el a második vagy harmadik feladatban. Így
2. dicsérettel jutalmazzuk
Bognár András Károlyt, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulóját (tanárai Ádám Réka, Dobos Sándor, Fazakas Tünde, Hujter Bálint és Rubóczky György),
Forrai Boldizsárt, az SZTE Gyakorló Gimnázium és Általános Iskola 10. osztályos tanulóját (tanárai Matos Zoltán és Torma Bence), valamint
Tarján Bernátot, a Békásmegyeri Veres Péter Gimnázium 12. osztályos tanulóját (tanárai Holló Gábor, Dobos Sándor és Nagy Zoltán Lóránt).
A versenybizottság ezúton köszöni meg minden versenyző, felkészítő tanár és a lebonyolításban közreműködő kolléga munkáját, a díjazottaknak pedig további sikereket kívánva gratulál.”
A feladatok megoldásai idén is a KöMaL februári számában (74. évf. 2. sz) jelentek meg.











