A Közép-Európai Matematikai Diákolimpiát 2013 után másodszorra rendezte hazánk, a 18. MEMO-nak idén Szeged adott otthont augusztus 24–30. között. A versenyen a szokásos 10 ország (Ausztria, Csehország, Horvátország, Lengyelország, Litvánia, Magyarország, Németország, Svájc, Szlovákia és Szlovénia) 6-6 fős csapatai vettek részt. A csapatok olyan diákokból álltak, akik a versenyt megelőző tanévben még nem érettségiztek. (A felkészülésről és a csapat kiválasztásáról az IMO2024-ről szóló cikkben olvashatnak.)
A magyar csapat tagjai Holló Martin (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 10. osztály), Keresztély Zsófia (Szent István Gimnázium, Budapest, 11. osztály), Kovács Benedek Noel (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 11. osztály), Molnár István Ádám (Földes Ferenc Gimnázium, Miskolc, 11. osztály), Prohászka Bulcsú (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 10. osztály) és Vigh Zalán (Szegedi Radnóti Miklós Kísérleti Gimnázium, 10. osztály) voltak, és a csapatot Kovács Benedek és Hegedűs Dániel (az ELTE TTK hallgatói) vezették.
A képen balról jobbra: Hegedűs Dániel, Kovács Benedek, Prohászka Bulcsú, Holló Martin, Keresztély Zsófia, Vigh Zalán, Kovács Benedek Noel, Molnár István Ádám (kezében a csapat kabalája, Marvin).
Két versenynapból állt a megmérettetés: az első napon egyedül, a második napon pedig csapatban gondolkodhattak a versenyzők a feladatokon. Az egyéni 4, a csapatverseny pedig 8 feladatból állt, a diákolimpiákon szokásos négy témakörből (algebra, kombinatorika, geometria, számelmélet). Minden feladatra 8 pontot lehetett szerezni.
Az egyéni versenyen a magyar diákok az alábbi eredményeket érték el:
Keresztély Zsófia a maximális 32 ponttal
aranyérmet és abszolút első helyezést,
Holló Martin 20 ponttal,
Vigh Zalán 19 ponttal,
Molnár István Ádám 18 ponttal,
és Kovács Benedek Noel 17 ponttal
bronzérmet,
Prohászka Bulcsú 10 ponttal
dicséretet szerzett.
A csapatversenyben 5. helyezést értünk el 47 ponttal, a második helyezettől mindössze 2 ponttal lemaradva. A lengyelek egymás után az ötödik évben szerezték meg újra a győzelmet. Az egyéni verseny eredményei itt, a csapatverseny eredményei pedig itt olvashatók.
Gratulálunk a csapattagoknak a szép eredményükhöz, és további sok sikert kívánunk szakmai pályafutásukhoz!
Köszönjük szépen a kísérőinknek, Jánosik Áronnak és Sánta Zsófia Grétának a velünk töltött időt, illetve a szervezői gárda (Lenger Dániel főszervező, valamint Bán-Szabó Áron, Dankowsky Anna Zóra, Győrffy Lajos, Hujter Bálint, Imolay András, Kosztolányi József és Makay Géza) áldozatos munkáját! Köszönet a javítóknak és mindenki másnak is, aki a rendezvényben bármilyen módon szerepet vállalt! Továbbá nagyon szépen köszönjük a Bolyai János Matematikai Társulat anyagi támogatását.
A következő MEMO a németországi Chemnitz városában, 2025. augusztus 25–31. között lesz.
Hegedűs Dániel (helyettes csapatvezető)
A verseny feladatai (magyarul is) itt érhetők el.
A versenyzők rövid megjegyzései következnek a feladatokról:
I-1: Az egyéni verseny első feladata egy egyismeretlenes függvényegyenlőtlenség volt. A MEMO 12 feladata közül ez volt a legkönnyebb, amit az is jól mutat, hogy az egyéni verseny első 28 helyezettje maximális pontot kapott rá. Különlegessége a feladatnak az volt, hogy nem az összes, a feltételnek megfelelő függvényt kellett megadni, hanem az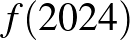 
lehetséges értékeit.
I-2: A következő egy izgalmas kombinatorikus geometriai feladat volt. Be kellett látni, hogy korlátos sok adott típusú kérdéssel meghatározhatók egy rejtett konvex sokszög csúcsai. A feladat szépsége, hogy ez elsőre nem is feltétlenül intuitív állítás, helyette véges, de nem korlátos sok kérdésre tűnik hihetőnek a feladat. Azonban a szépség itt ki is merül, hiszen sok irányba lehet menni az algoritmus megkonstruálásával, és iránytól függően kicsit vagy nagyon lesz kellemetlen mind a leírás, mind a koordinálás. Ráadásul a kamu megoldás esélye sem elhanyagolható, sajnos több csapattag is belefutott ebbe a hibába.
I-3: Azt kellett belátni, hogy 3 pont körülírt köre áthalad egy fix ponton. A fixpont megsejtése után a feladat kijön szögszámolással és hasonlóságokkal, de született Pascal-tételes megoldás is. A fixpont megsejtése sem volt olyan nehéz, viszont abból következett egy olyan tengelyes szimmetria, amit sokak nehezen hittek el.
I-4: Ez a feladat egy egész együtthatós polinom helyettesítési értékeinek oszthatóságával foglalkozott, amit 3 csapattag 3 különböző módon oldott meg. A megoldás megsejtése itt is nagyon sokat segített a bizonyításhoz, és nem is volt nehéz megsejteni, lévén, hogy elég hihetetlen az állítás. A legtöbb megoldás teljes indukciót használt, illetve azt az ismert tényt, hogy csak a 0 osztható minden prímmel. Emellett sokan a Dirichlet-tétel használatától sem riadtak vissza.
T-1: A feladatban azt kellett bebizonyítani, hogy egy sorozat két tagjának összege legalább 88. Némi átalakítások után egy másik összegről próbáltuk bebizonyítani, hogy legalább 88. Ez a verseny végére maradt. Az utolsó percekben próbáltuk integrálással alábecsülni az összeget, de csak azt tudtuk bebizonyítani, hogy legalább kb. 87. Mint kiderült, a tényleges összegünk csak kb. 87,5, így a megoldásrészletünk nem javítható.
T-2: A nehezebb algebra feladat egy valós kétváltozós függvényegyenlet volt. Nem nagyon különleges, de nem is túl egyszerű feladat. A nehéz csapatfeladatok közül valószínűleg ez volt a legkönnyebb. A fő ötlet az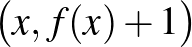 
számpár behelyettesítése volt, innen pedig általánosabb ötletekkel, mint az injektivitás, a linearitás és a 0 felvételének vizsgálatával fejezhető be a feladat.
T-3: Ez a feladat az egyéni verseny után egy újabb kitalálós játék volt, és minimális kísérletezéssel könnyen megoldhatónak bizonyult.
T-4: A nehezebb kombinatorika feladatra nem maradt túl sok ideje a csapatnak, de Bulcsúnak és Zalánnak sikerült az utolsó egy órában leírni egy hasznos lemmát, amire kapott a csapat egy pontot. Rajtunk kívül csak a csehek és a szlovákok kaptak erre a feladatra pontot – igaz, hogy ők többet, mint mi.
T-5: Az első geometria feladat a csapatverseny legkönnyebb feladata volt. A példában két kör szerepelt, és több egyenlő hosszú szakasz. Az állítást – hogy három pont egy egyenesre esik – rövid szögszámolás, egy szabályos háromszög és egy rombusz megtalálása után gyorsan be is lehetett bizonyítani.
T-6: A csapatverseny nehezebb geometria feladata viszonylag bonyolultabb ábrával rendelkezett, ami három beírt kört is tartalmazott. A feladat állítása két egyenes merőlegessége volt. A megoldás alapvetően két főbb gondolatot igényelt. Az első egy jó sejtés volt, miszerint az egyik kör középpontja egyben magasságpont is egy másik háromszögben. A másik fontos lépés egy ügyes tükrözés volt, majd egy húrnégyszög megtalálásával és szögszámolással be lehetett látni a beírt kör középpontjáról, hogy egyben magasságpont is, és ezzel befejeződött a feladat megoldása.
T-7: Ennek a feladatnak a csapatverseny két számelmélet-feladata közül elvileg a könnyebbnek kellett volna lennie, de egyedül a magyar csapat kapott erre a feladatra több pontot, mint a másikra. A feladatban az első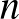 
számot kellett megfelelő sorrendben egymás mögé leírni úgy, hogy a számokat egybeolvasva a kapott szám osztható legyen egy rögzített 
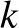számmal. Azokat a 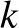számokat kellett megtalálni, ahol ezt véges sok 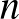kivételével mindig meg lehet csinálni. A feladatra a válasz intuitívan elég egyértelmű volt, de a bizonyítása már nem volt olyan egyszerű.
T-8: Ez volt a nyolc közül a másik feladat, amiről nem hitte azt a csapat, hogy megoldottuk, de Benedek sokat gondolkozott rajta, össze is szedett 2 pontot.
A szegedi diákolimpiáról az Érintő következő számában további írásokat jelentetünk meg, közöljük a versenyzők részletes megoldásait, élménybeszámolójukat és Győrffy Lajos MEMO programfelelős cikkét az első napra szervezett városi vetélkedőről. (A szerk.)