Elhunyt Pelikán József

Pelikán József, az ELTE Algebra és Számelmélet Tanszékének nyugalmazott adjunktusa, az algebra lenyűgöző tudású oktatója, a matematikai versenyeknek diákkorában rendkívül sikeres résztvevője, majd évtizedeken át vezető személyisége, 2023. január 20-án váratlanul elhunyt.

A Fazekas Gimnázium legendás legelső speciális matematika tagozatos osztályának diákja volt 1962–1966 között. Kiváló versenyző volt. Csak a legkiemelkedőbb eredményeit sorolva: mind a négy gimnazista évében részt vett a Nemzetközi Matematikai Diákolimpián, először ezüstérmet, azután háromszor aranyérmet szerezve, ezáltal a 12–18. helyet foglalja el a diákolimpiák örökranglistáján. 1963-ban és 64-ben korosztályában első lett a Középiskolai Matematikai Lapok pontversenyében. 1964-ben megnyerte a Magyar Televízió „Ki miben tudós?” vetélkedőjét. 1965-ben győzött az Országos Középiskolai Tanulmányi Versenyen, középiskolásként (!) második díjat kapott a Schweitzer Miklós Emlékversenyen, a Kürschák versenyen szintén második díjat nyert.

Az aranygyűrűs doktori fokozatot Ádám György, az ELTE rektora adja át Berkes Istvánnak és Pelikán Józsefnek (1975). A fotó Staar Gyula: A matematika emberi arca c. könyvében jelent meg (Vince Kiadó, 2020)

Pályája során fontos szerepeket töltött be a matematikai versenyek irányításában és a diákok felkészítésében. A Kürschák József Matematikai Tanulóverseny bizottságának 1972-től 2018-ig volt tagja, ebből nyolc alkalommal titkára. A magyar matematikai diákolimpiai csapatnak harmincegy alkalommal (1988-ban, majd 1990-től 2019-ig) volt a vezetője. Átfogó matematikai tudásával és széleskörű nyelvismeretével nagy tekintélyt vívott ki az olimpiákon résztvevő csapatok vezetőinek körében. Ennek köszönhetően megválasztották az irányító szerv, az Advisory Board tagjának, majd elnökének, amely tisztséget nyolc éven át töltötte be. Munkájának elismeréseképpen a World Federation of Mathematics Competitions szervezettől 2014-ben Erdős-díjat kapott.

A Bolyai János Matematikai Társulatba 1969-ben lépett be. A versenyek mellett több más területen is dolgozott a Társulatban: a Tudományos Szakosztály titkáraként (1972–1985), a Matematikai Lapok szerkesztőbizottságának tagjaként (1980-tól), a Választmány tagjaként (1985-től) és a küldöttgyűlések szavazatszámláló bizottságának vezetőjeként (1978–2018). Gazdag munkásságáért a Társulat 2020-ban Beke Manó-nagydíjjal tüntette ki.

Tudományos érdeklődésének fő területe az absztrakt algebra volt. Hatalmas olvasottságának köszönhetően otthon volt az algebra szinte összes területén, változatos témákból hirdetett speciális előadásokat. 1971-től 2020-ig tanított az ELTÉ-n. Az első- és másodéves matematikus hallgatóknak tartott „bevezető” algebra előadásai igen messze és mélyre vezettek, előadói stílusa és lenyűgöző tudása lebilincselte hallgatóit, évtizedek múltán is meghatározó élményként emlegetik Jocó előadásait. Kutatóként sajnos nem volt olyan sikeres, mint versenyzőként: tíz tudományos dolgozat szerzője.

Versenyzői és csapatvezetői tevékenysége a matematikán kívül a bridzséletben is jelentős volt. 1986-ban tagja volt a Taurus csapatának, amely második lett a BEK-ben. Az Európa-bajnokságokon 1985-ben a magyar női, majd 1989-ben és 1991-ben a férfi (nyílt) válogatott kapitánya volt.

Életútjának rövid összefoglalását néhány személyes emlékkel egészítjük ki, valamint egyik dolgozatának eredményeit részletesen bemutatjuk.

(Lovász László) A Fazekas Gimnáziumban a matematika órák egy részén hármunkat (Pósa Lajossal együtt) Rábai tanár úr felmentett a részvétel alól, feltéve, hogy a hátsó padokban (viszonylag) csöndben matematikával foglalkozunk. Folytak ugyan sakkjátszmák is, de betartottuk, hogy a matematikával való foglalkozás kellett, hogy domináljon. Nagyon sokat tanultunk egymástól ezek alatt az órák alatt.

Jocó legtöbbet idézett cikke egy közös cikkünk, On the eigenvalues of trees, amin az egyetem elvégzése utáni nyáron egy nyári iskolán kezdtünk gondolkodni, és pár hónappal később nyújtottuk be közlésre a Periodica-hoz. Az a tény, hogy egyáltalán lehet kapcsolat egy gráf adjacencia-mátrixának sajátértékei és gráfelméleti tulajdonságai között, igen friss és meglepő volt, és néhány egyszerű, de nem-triviális tételt sikerült bebizonyítanunk. Jól össze tudtuk tenni Jocó széles és mély algebrai tudását és az én gráfelméleti ismereteimet. A cikkben bevezetett fogalmak és ezek az első eredmények később a kémiában leltek alkalmazásra, ahol ma is írnak a „Lovász–Pelikán index”-ről.

(Lovász László és Vesztergombi Katalin) Fiatal egyetemi oktatóként írtunk Jocóval hárman egy szakköri füzetet Kombinatorika címmel. Eredetilag általános iskolásoknak szántuk, de már a bírálók is szóvá tették, hogy nem építettünk ugyan szinte semmilyen előzetes ismeretre, de így is túl nehéz volt általános iskolásoknak (kivéve talán a legtehetségesebbeket), és végül mint „Általános és Középiskolai Szakköri Füzet” jelent meg. Ezt a kis munkát több nyelven is kiadták.

Sokkal később, a 90-es években, a Yale egyetemen tanítottunk, és úgy láttuk, hogy régi könyvecskénk anyaga jól használható volt „kedvcsináló” kurzusokhoz diszkrét matematikából. Persze, a használathoz angolra kellett fordítani, és nagyon sok részletet megváltoztatni, kiegészíteni. Megkerestük Jocót, hogy nem volna-e érdemes egy jelentősen kibővített angol változatot kiadni, és ő lelkesen felvállalta, hogy beszáll a munkába. Így jött létre a Springer kiadónál megjelent Discrete Mathematics: Elementary and Beyond című könyvünk, melyet aztán ugyancsak több nyelvre is lefordítottak (ideértve a magyart is). Mindhárman élveztük a régi együttműködés felelevenítését, emlékeinek felidézését.

(Szegedy Balázs) Pelikán Jocó mitikus alak volt, legalábbis számomra és a közeli barátaim számára is. Terjedelmes megjelenése karizmatikus kisugárzással párosult. Anélkül volt tiszteletet parancsoló, hogy a hagyományos értelemben vett tisztelet szertartásait megkövetelte volna. Sőt elutasította. Már a legelső előadáson jelezte, hogy nehogy véletlenül magázzuk és hogy hívjuk csak Jocónak. Azt is mondta, hogy a szóbeli vizsgára akár fürdőruhában is jöhetünk. (Az öltöny másutt akkoriban alap volt.) Pontosan értettük, hogy ez nem lazaságot jelent, hanem azt, hogy igen sokat fog követelni. És ez így is lett. Egyik zh-mra hármast adott, pedig rengeteget készültem rá. Jocó megdicsért, mert így is az egyik legjobb lett. Ritkán voltam olyan büszke az egyetemen, mint erre a hármasra. A gyakorlati jegyhez összeadta a ZH jegyeket, így nem volt gond végül. A fürdőruhás állítását pedig leteszteltük: Egyik évfolyamtársammal fogadtam 500 forintban (a 90-es évek elején ez nagy pénz volt), hogy nem mer bemenni a vizsgára fürdőruhában. Máig röhögök, mikor visszagondolok, hogy az évfolyamtársam a folyosón ledobta a ruháját, felkapott egy fecskét és lazán besétált a vizsgára. Jocó jól mulatott és végül négyest adott, ami igen jó jegynek számított nála.

Sajnos az egyetemen igen sokat lógtam, de Jocó óráját sosem hagytam ki. Kifejezetten szórakoztatónak találtam az előadásait. Mint később megtudtam, ez nála tudatos volt. Állítólag ő maga mondta, hogy az órának egyben egy show-nak is kell lennie. Imádott hatni a hallgatóságra néha egészen extravagáns állításokkal. Mikor a bilineáris formákat tanultuk és kimondta, hogy „nem-elfajuló Hermite-féle szeszkvilineáris forma”, elmosolyodott es hozzátette, hogy „ha ezt egy utcaseprőnek mondanám, akkor jól pofán vágna”. Mikor a lineáris algebrát kezdte tanítani, úgy vezette be, hogy „ez az algebra legunalmasabb és egyben a leghasznosabb része”. Ezt is nagyon jól tanította. Parasztos egyszerűséggel mondta el a mátrix-szorzást. Mikor egyszer német diákoknak elmondtam, hogy Jocó hogyan tanította, csodálkozva mondták, hogy ők sajnos nem így tanulták és igen hálásak voltak a tudásért. Jocónak szinte védjegye volt a parasztos egyszerűség es egy tiszteletet parancsoló nagyság egyedi keveréke.

Harmadév körül írtam az első cikkem csoportok reprezentációiról. Ez volt az egyik kedvenc témám, amit Jocó úgy tanított, hogy abból világos volt, hogy nagyon szereti. Teljesen meggyőzött, hogy ez az egyik legvagányabb téma, ami létezik és részben ez tüzelt fel arra, hogy próbáljak megoldatlan kérdéseken is gondolkozni a témában. Emlékszem, hogy igyekeztem olyan egyszerűen és tisztán gondolkozni, mintha Jocó gondolkozna a fejemben. Ilyen módon nagyban segítette a kutatói személyiségem kialakulását.

Jocó nem csak hatásos tanár volt, de stílusformáló erő. Szavajárása, humora, habitusa ragadós volt. Több barátomon is észrevettem ennek a nyomait, akiket tanított és akiknek fontos volt. Ezt egészíti ki, hogy egyetemista korom kocsmai anekdotáinak gyakori szereplője volt. Szerettünk róla beszélni, és ezt nem minden tanárunk érdemelte ki.

(Pálfy Péter Pál) Az 1973-as diákolimpiára betegsége miatt Reiman tanár úr nem tudott kiutazni, Jocó ugrott be helyettes csapatvezetőnek, és jött velünk Moszkvába, illetve – másokkal együtt – a felkészítésünkből is kivette a részét. Csapatunk sikeres szereplésének megünneplésére vett egy üveg pezsgőt, szállodai szobájában összegyűltünk, ám annyira felrázódott az üveg, hogy nemcsak a dugója lőtt ki, hanem a nemes ital jó része is szerteszét spriccelt, így nem sok jutott egy-egy csapattagnak. Társaimmal azóta is emlegetjük ezt az epizódot. A csapat jó eredményében bizonyára annak is szerepe volt, hogy Jocó minden kis pontocskáért megküzdött a koordinátorokkal. Nekem is szerzett egy pontot azzal, hogy ahol a kitevőben levő különbséget – értelmetlenül – zárójelbe tettem, azt kimagyarázta, hogy csak görbére sikerült az abszolút érték jele – az kellett volna ugyanis a jó megoldáshoz.

Az egyetemen gyakorlatvezetőm volt Jocó, és én is úgy jártam, mint Szegedy Balázs. Bár már akkor elköteleződtem az algebra iránt, míg más tárgyakból könnyedén megírtam ötösre a dolgozatokat, az algebra zh-mra hármast kaptam. A felsőbb évfolyamokon több specijére jártam, lenyűgözött, ahogy nagyon összetett bizonyításokat érthetővé, követhetővé tudott tenni. Hírhedt szigorúsága az évek teltével enyhült, amikor együtt szigorlatoztattunk, akkor leggyakrabban azonosan ítéltük meg a vizsgázók teljesítményét, ha pedig mégis különböző jegyet gondoltunk adni, akkor általában én ajánlottam a gyengébbet.

(Szőnyi Tamás) Az Algebra előadást valószínűleg először az 1976-ban indult matematikus évfolyamnak tanította Pelikán Jocó. Másodéven vette át az évfolyamot, rövid idő alatt befejezte a lineáris algebrát, majd áttért absztrakt algebrára. Előadásai nagyon koncentráltak, mélyek, motiválóak voltak. Figyelembe véve az előadások sebességét is, voltak, akik nem, vagy csak nehezen vették fel a tempót, de az évfolyam jelentős részét terelte az algebra irányába, olyanokat is, akik később egészen más területen kezdtek dolgozni. Számukra meghatározó élményt jelentettek Jocó előadásai.

Jocónak az 1969 augusztusi balatonfüredi konferencia kötetében publikált dolgozata blokkrendszerekhez kapcsolódik. A blokkrendszer blokkjai valamely 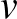$v$ -elemű alaphalmaz bizonyos 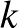$k$ -elemű részhalmazai, melyekre az is teljesül, hogy bármely két ponton ugyanannyi blokk megy át. Más terminológiával ezeket BIBD-nek szokták nevezni (balanced incomplete block design). A dolgozat három blokkrendszerekre vonatkozó izgalmas és aktuális kérdést vizsgál. Az első a 2-3 BIBD-ek létezése, azaz a 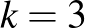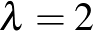$k=3$ , $\lambda=2$ eset vizsgálata (a 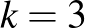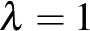$k=3$ , $\lambda=1$ eset a klasszikus Steiner-hármasrendszerek esete). Ezekre több szép rekurzív konstrukciót ad meg, amelyek segítségével minden olyan 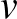$v$ -re, ami nem 2 maradékot ad 3-mal osztva meg tud adni ilyen 2-3 BIBD-et. Kiindulásul a 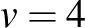$v=4$ , 6, 7 esetben egy-egy konkrét példát mutat. A másik probléma a BIBD-k kromatikus számának meghatározása. Ezzel kapcsolatban belátja, hogy minden Steiner-hármasrendszer kromatikus száma legalább 3 és megkezdi a kételemű test fölötti projektív terek vizsgálatát. A kérdés aktualitását és érdekességét mutatja, hogy Alex Rosa lényegében ugyanekkor kezdte meg a kérdés vizsgálatát.

A dolgozat legnagyobb része BIBD-ek reprezentáns rendszereivel foglalkozik, és itt is három problémát vizsgál. Ezek olyan ponthalmazok, amelyek minden blokkot metszenek. Manapság lefogó ponthalmaznak szokták nevezni, és véges geometriákban vizsgálatuk fontos szerepet játszik. Jocó belátta, hogy egy ilyen reprezentáns rendszer legalább 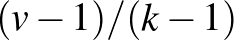$(v-1)/(k-1)$ pontot tartalmaz, és egyenlőség esetén a pontok rész-BIBD-t alkotnak. Ez egy nagyon általános és elegáns tétel, melynek azonnali következménye, hogy projektív térben a legkisebb, egyeneseket lefogó ponthalmaz hipersík. Figyelmét a projektív síkokra koncentrálja és megvizsgálja, hogy mi a legkisebb egyenest nem tartalmazó lefogó ponthalmaz legfeljebb hetedrendű síkokon, továbbá példát ad 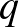$q$ -adrendű, testre épített projektív síkban 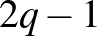$2q-1$ és annál kevesebb pontú lefogó ponthalmazokra. Érdemes megjegyezni, hogy a kisrendű síkokról ugyanebben az évben jelent meg Jane Di Paola egy cikke (aki még a 8- és 9-rendű síkokat is el tudta intézni). A legérdekesebb rész Jocó cikkében a legkisebb, egyenest nem tartalmazó lefogó ponthalmaz méretére adott alsó becslése, nevezetesen, hogy ez legalább 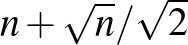$n+\sqrt{n}/\sqrt{2}$ , azaz az egyenes méreténél ( 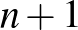$n+1$ -nél) jóval nagyobb. Itt Aiden Bruen lényegében ugyanekkor tudott egy még jobb alsó becslést bizonyítani 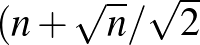$(n+\sqrt{n}/\sqrt{2}$ helyett $n+\sqrt{n}+1$ -et látott be, ami bizonyos esetekben éles). Bárány Imre információja szerint kicsit később, kijevi részképzése során Jocó is belátta az éles alsó korlátot, de azt már nem publikálta, mivel Bruen dolgozata(i) időközben megjelent(ek). Mindkét bizonyítás kombinatorikus, de lényegesen különböznek.