Tau nap – de most tényleg?

Sok szeretettel és mély tisztelettel ajánlom ezt az írást Herczeg Jánosnak, egykori matematikatanáromnak, aki matematikán túl emberségre is tanított, akitől elleshettem a tanári szakma néhány alapfogását. Legutóbb megígértem neki, hogy lesz még folytatása a 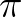$\pi$ -ről szóló cikknek... Tanár úr, ez lenne az..., csak ezt sajnos Ön már nem olvashatja.

Azt írja Halmos Pál How to write mathematics? című cikkében¹, hogy igyekezzünk minél kevesebb jelet használni, és próbáljuk meg elkerülni, hogy azok rögzített jelentéssel szerepeljenek. Pedig elképzelhetetlen, hogy a koordináta-rendszer tengelyeit ne 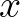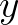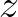$x$ , $y$ , $z$ jelölje, vagy hogy a természetes alapú logaritmus alapszáma ne 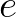$e$ , a parciális deriválás jele ne 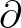$\partial$ (vajon milyen jel is ez?) legyen.

És az a sok betűtípus! A vektorokat félkövér, a halmazrendszereket írott, a kategóriákat gót betűkkel írjuk. A geometriában a szögeket, az analízisben a „kicsiny, de pozitív mennyiségeket” görög, a számosságot héber betű jelöli, és még mi minden van! Kész káosz!

Na meg aztán ott van az a hányatott sorsú 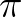$\pi$ , amit végképp lehetetlen lenne egyszer csak más betűvel jelölni. Pedig görög betű, és mint ilyen, feltételezhető, hogy szöget jelöl. Hát, ahogy vesszük, akár az is lehet! Az egyenes szög mértéke.

Erre felbukkan Michael Hartl², a 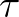$\tau$ Manifesto (kiáltvány) alapítója, és azt javasolja, hogy a teljes szöget jelöljük 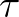$\tau$ -val. A kör kerülete ezek szerint 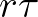$r\tau$ (na, tessék, még egy berögzült jelölés: 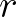$r$ a kör sugara). Én ugyan eddig is le tudtam írni a kör kerületét két jellel: 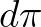$d\pi$ (na, igen, újabb berögzült jel, 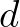$d$ a kör átmérője). Azt viszont elhallgatja Hartl, hogy a kör területe így $\dfrac{r^2\tau}{2}$ . Brrr!

Hartl azt állítja például a Google központban 2010-ben tartott előadásában³, hogy ő Bob Palais 2001-ben megjelent cikkére⁴ reagált. Palais szerint ugyanis a 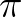$\pi$ csak a kör fele, a teljes fordulat mértéke 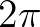$2\pi$ , ennek jelölésére a 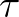$\tau$ -t javasolja. Ráadásul magára a jelre is szolgál kellő magyarázattal. Míg a 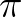$\pi$ a periféria, kerület szó első (görög) betűje, a 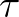$\tau$ a görög τορνοσ [tornosz], vagyis fordulat kifejezés kezdőbetűje. Hozzáfűzi még, hogy a 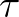$\tau$ olyan, mint egy 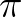$\pi$ , aminek eltávolították az egyik lábát. A kampány valódi indoka pedig az, hogy rengeteg képletben szerepel a 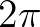$2\pi$ , amit nyilván egyszerűbb lenne egyetlen jellel írni.

Azt is megtudhatjuk a videóból, hogy Joseph Lindenberg már 1991-ben foglalkozott ezzel a kérdéssel, és ő már akkor javasolta, hogy az egység sugarú kör kerületét jelöljük 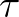$\tau$ -val. Lindenberg még egy honlapot is szentelt a témának „mielőtt menő lett a 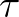$\tau$ ”: tau before it was cool.

Hartl elismeri, hogy van hátránya egy új konstans bevezetésének, például vannak más konstansok, amelyeket 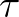$\tau$ jelöl, de felhívja rá a figyelmet, hogy több más konfliktus is van a műszaki jelölésrendszerben, mégis mindenki érti, melyik képlet mit takar. Azután hosszan sorolja az előnyöket, amelyekkel viszont sokat nyerhetünk.

A 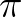$\pi$ két tizedesre kerekítve 3,14 – innen jött az ötlet, hogy a 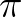$\pi$ -t a harmadik hónap 14. napján, március 14-én ünnepeljük. A 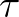$\tau$ két tizedesjegyre kerekítve 6,28 – logikus tehát, hogy ünnepeljük a 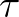$\tau$ -t június 28-adikán.

Hát, jó! Ünnepeljük a 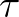$\tau$ -t! Szeretem az ünnepeket!

... nem akarok ünneprontó lenni, de a 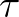$\tau$ jel inkább a fele a 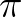$\pi$ jelnek. Választhattunk volna jobbat a 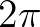$2\pi$ jelölésére, például $\pi\kern-5pt\pi$ . És hogy nincs ilyen? Annál jobb, így felszabadul egy görög betű a szögek jelölésére.

Fried Katalin
ELTE TTK
Matematikai Intézet

Lábjegyzetek

: ¹A cikk eredetileg angolul jelent meg, amelyben többször szó esik a jelek ideális megválasztásáról, a magyar fordításból sajnos ez kimaradt. Az angol nyelvű cikk a https://bookstore.ams.org/hwmAmerican Mathematical Society (1973) kiadásában jelent meg, a magyar fordítást a Természet Világa: Természettudományi Közlöny, 1977, 12. száma 556–561. oldalán közölte.
: ²2010, https://tauday.com/
: ³https://youtu.be/k7MuXCOlE6M
: ⁴ 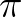$\pi$ is wrong – a 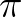$\pi$ hibás – The Mathematical Intelligencer Springer-Verlag New York Volume 23, Number 3, 2001, pp. 7-8., http://www.math.utah.edu/~palais/pi.pdf