Könyvajánló „A matematikai populációdinamika rövid története” című alkotáshoz, avagy izgalmas olvasmány a matematika és a tudománytörténet iránt érdeklődőknek

1. Kicsiknek és nagyoknak is
„A matematikai populációdinamika rövid története” című könyv magyar nyelvű változata ingyenesen elérhető az alábbi weboldalon: http://www.ummisco.ird.fr/perso/bacaer/hu.pdf.
Kaptam az alkalmon és gyorsan nekiláttam: izgalmas olvasmánynak ígérkezett, tekintve hogy a járványterjedés modellezésével foglalkozom. Mint a könyv bevezetőjében is olvasható, a populációdinamika az a tudományterület, amely egyszerű mechanisztikus módon próbálja megmagyarázni a biológiai populációk méretének és összetételének időbeli változásait. A populációdinamika több tudományterület – a matematika, a társadalomtudományok (demográfia), a biológia (populációgenetika és ökológia) és az orvostudomány (epidemiológia) – metszéspontjában áll, így a téma sokféle szemszögből bemutatható. Jó ötletnek tartom, hogy a szerzők más irányból közelítettek és a történeti szempont kerül előtérbe, emellett a jelentősebb populációdinamikai kutatások matematikájával is megismerkedhetünk.
A könyv felépítése a következő: 26 fejezetet tartalmaz, amelyekben egy-egy jelentősebb – a témához kapcsolódó – elméletet mutatnak be a teljesség igénye nélkül. Az egyes fejezetek elején található egy tömör összefoglaló, ezt követi a kutatók rövid életrajza. A könyv így a matematikában kevésbé jártasak, viszont a tudománytörténet iránt érdeklődők számára is érdekes olvasmány lehet. De a matematika szerelmesei se maradnak kielégítetlenül: a fejezetekben a matematikai elméleteket, modelleket is bemutatják, a számítások részleteivel és bizonyításokkal is megismerkedhetünk vázlatosan, diagramok és táblázatok is segítik a megértést. Azonban a műnek nem célja a matematikai finomságok mélyére ásni: nem kell matematikus diploma az elméletek megértéséhez, a bonyolultabb matematikai részletek akár át is ugorhatóak. A szerzők a könyvet főként lelkes középiskolásoknak, egyetemi hallgatóknak és matematikatanároknak ajánlják, de bárki élvezettel forgathatja az alkotást, aki informálódna a matematika, a tudománytörténet, a demográfia vagy akár az epidemiológia populációdinamikai vonatkozásaiban. Az írók az olthatatlan kíváncsisággal megáldott olvasókra is gondolnak: az egyes fejezetek végén részletes hivatkozási listák találhatóak, esetenként olyan linkekkel, amelyekről az eredeti publikációk letölthetők (1. ábra).
1. ábra. A hivatkozások az eredeti műveket bemutató oldalakra kalauzolhatnak minket.
A könyv a fontosabb populációdinamikai elméletek kialakulását mutatja be kronológiai sorrendben napjainkig. Az egyes fejezetek külön-külön is olvashatóak, de bizonyos fejezetek témái egymáshoz kapcsolódnak. A szerzők igyekeztek rendszert teremteni a bemutatott elméletek között: a fejezetekben jelzik, ha a témáról más kutatást, továbbfejlesztést is ismertetnek egy későbbi részben. Számomra hasznosnak bizonyult egy önkényes kategorizálást készíteni a könyv nagyobb témaköreihez a jobb áttekinthetőség kedvéért: betekintést nyerhetünk a populációk növekedésére vonatkozó tézisekbe (1., 3., 5., 6., 10., 13., 16., 21., 24., 25. fejezetek), a járványterjedés korai modelljeibe (4., 12., 16., 22. fejezetek), a populációgenetika kezdeteibe (8., 11., 14., 17., 19., 20. fejezetek), az evolúció folyamatának megértésébe (15., 23. fejezetek) és a kihalási probléma kezelésébe (2., 7., 9., 18. fejezetek) is. Személyes érdeklődésem alapján az első két témakörrel az ajánlóban később részletesebben foglalkozom. (A könyvből néhány eredeti mondatot is tartalmaz a következő két szakasz.) Az utolsó fejezet a populációdinamika számos izgalmas kortárs problémáját tekinti át röviden, mint például a népesség elöregedése a demográfiában, új betegségek (AIDS, SARS, stb.) és a vakcinázási politika a járványtanban, illetve a halászati politika az ökológiában.
Ez a könyv lényegében Nicolas Bacaër 2008-as „Histoires de mathématiques et de populations” című művének fordítása. A könyv végén található ezzel kapcsolatban egy érdekes gondolat: „A gépi fordításban elért legújabb eredményeknek köszönhetően a tudományos szakirodalomban az egyetlen nyelv virtuális monopóliuma már nem indokolt. Az egyetemeken tapasztalható növekvő nyelvi elidegenedés visszafordítható. Ezzel a gondosan átdolgozott magyar fordítással erre az új útra buzdítunk.” Én üdvözlöm ezt a törekvést: valóban üdítő élmény volt az anyanyelvemen olvasni a témáról. A könyv bevezetőjéből kiderül, hogy a szerzők a DeepL szoftver automatikus fordítóját is használták a könyv elkészítése során. Sajnos a könyv a gépi fordítás részleteire és tapasztalataira nem tér ki. Szívesen olvastam volna erről egy rövid összefoglalót: Vajon a teljes francia művet így fordították le, vagy csak egyes részeit? Mennyire volt pontos a fordítás, sok hibát tartalmazott-e? Milyen nehézségekkel szembesültek a munka során és hogyan oldották meg őket?
A könyv logikusan van felépítve, jól érthető, olvasmányos és izgalmas alkotás. A szerzők alapos munkát végeztek, a matematikai számításokat precízen átnézték (olyannyira, hogy esetenként még hibákat is felfedeztek a tudósok eredeti kalkulációiban). A művet azoknak ajánlom, akiket érdekel, hogy az utóbbi évszázadok kutatóit a világ mely problémái foglalkoztatták és hogyan próbáltak rájuk megoldást találni, illetve azoknak, akiket érdekel, hogy a most használatban lévő matematikai fogalmaknak és elméleteknek kik rakták le az alapköveit. Véleményem szerint a könyv jól használható olyan középiskolai vagy egyetemei ismeretterjesztő kurzusokon is, ahol az egyes fejezeteket a hallgatók dolgozzák fel, majd előadás formájában prezentálják az órán, de az oktató által összeválogatott előadás-sorozatnak is az alapja lehet. A könyv bevezetésként szolgálhat a matematikai modellezés világába, emellett a hivatkozási listák a további kutatómunkát is segíthetik.
2. Populációk növekedésére vonatkozó modellek
Sok kutató érdeklődését felkeltette, hogy az egyes populációk hogyan növekednek. A kapcsolódó fejezetek feldolgozása során szépen nyomon követhetőek a populációs modellek egyes fejlődési szakaszai. A továbbiakban néhány jelentős eredményt, illetve érdekességet emelek ki, amelyek kedvcsinálók lehetnek az olvasáshoz.
Az 1. fejezet a nyúlpopuláció növekedésének leírására használt Fibonacci-sorozatról szól, ami az egyik legkorábbi populációdinamikai probléma megoldása. 1202-es könyvében mutatta be Fibonacci a ma közismert rekurzív sorozatot, viszont a XIX. századig (amikor kiadták Fibonacci összes művét) a nyulakkal kapcsolatos példája és megfigyelései feledésbe merültek, és nem befolyásolták a matematikai populációdinamikai modellek fejlődését.
A következő jelentősebb elméletek megjelenésére a XVIII. századig kell várnunk, ekkor Leonhard Euler a népesség exponenciális növekedését vizsgálta több modell segítségével (3. fejezet). Ez a munka a XX. században kidolgozott, a demográfiában fontos szerepet játszó stabil népességelmélet előfutára. Euler azt állította, hogy a 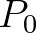 kezdeti állapotból kiindulva,
kezdeti állapotból kiindulva, 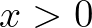 növekedési ráta mellett az
növekedési ráta mellett az 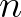 -edik évi népesség a következőképpen adódik:
-edik évi népesség a következőképpen adódik:
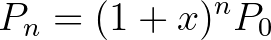
Ezt hívjuk geometriai vagy exponenciális növekedésnek. Euler több példát ismertetett a népesség exponenciális növekedésére, és a számításaihoz a 1614-ben John Napier által bevezetett logaritmus fogalmát is felhasználta. Egy kedves példája – amiről a fejezetben említést tesznek – Noé bárkájának történetéhez kapcsolódik: a matematikus kiszámolta, hogy ha az özönvíz után minden ember egy hatfős népességből származik, és feltételezzük, hogy a népesség kétszáz évvel később egy millió fő volt, akkor az éves növekedési ütem 6,25 százalékos. Ez nem tűnt számára irreálisnak, így vallásos emberként és matematikusként sem kérdőjelezte meg a bibliai történet igazságtartalmát. További észrevétele volt, hogy ha feltételezzük, hogy a növekedés ilyen ütemben folytatódna tovább évszázadokig, akkor a Föld nem lenne képes fenntartani az emberiséget. Ezt a gondolatmenetet Thomas Malthus később továbbfejlesztette (5. fejezet): azt állította, hogy az élelmiszer-ellátás nem tudja hosszú ideig követni az emberi népesség növekedésének exponenciális tendenciáját. Ha a népesség viszonylag állandó marad, az azért van, mert az emberiség egy része nyomorra, éhezésre és járványokra van ítélve: ezek azok a csapások, amelyek lassítják a népesség növekedését, és amelyek Malthus véleménye szerint a társadalom fejlődésének legfőbb akadályai. Malthus tézisei befolyásolták Darwin és Wallace evolúcióelméletét, Marx kritizálta, de a gyakorlatban is megvalósult a kínai egykepolitikával. Érdekes arról olvasni, hogy napjaink égető problémájára, a túlnépesedés kérdésére már a korábbi évszázadokban is sok kutató tekintett aggodalommal.
2. ábra. Euler (1707–1783)
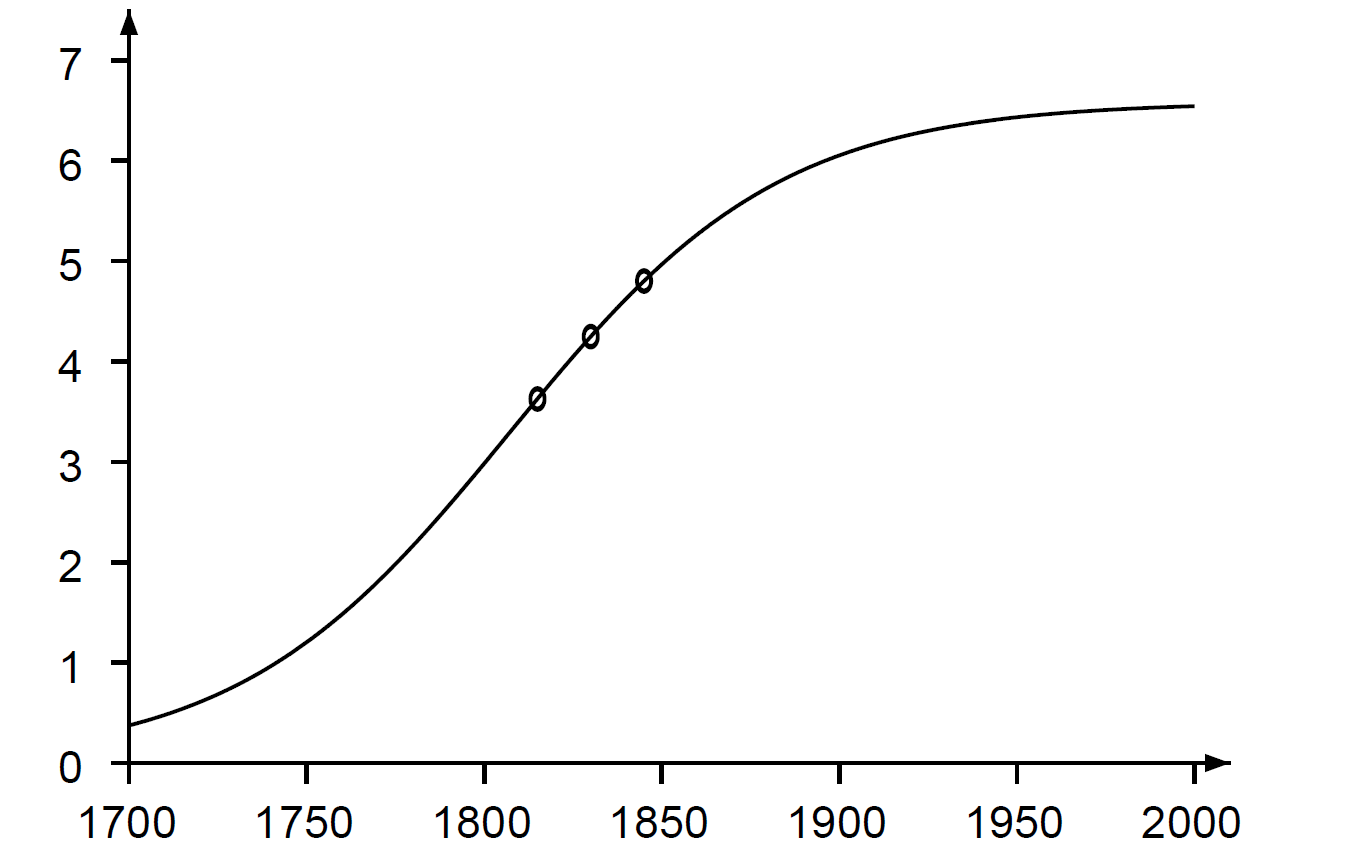
A Föld eltartóképességének végességét is figyelembe véve Verhulst előállt egy realisztikusabb modellel, a logisztikus egyenlettel (6. fejezet):
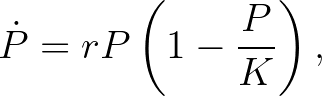
ahol 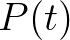 a populáció mérete a
a populáció mérete a 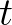 időpontban,
időpontban, 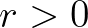 paraméter,
paraméter, 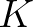 pedig a maximális populáció-létszám, ami később eltartóképesség néven vált ismertté. Verhulst belátta, hogy ha populáció mérete kicsi a
pedig a maximális populáció-létszám, ami később eltartóképesség néven vált ismertté. Verhulst belátta, hogy ha populáció mérete kicsi a 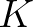 paraméterhez képest, akkor a növekedés közelítőleg exponenciális és
paraméterhez képest, akkor a növekedés közelítőleg exponenciális és 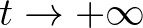 esetén a populáció
esetén a populáció 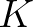 -hoz tart monoton növőleg (3. ábra).
-hoz tart monoton növőleg (3. ábra).
3. ábra. Belgium lakossága (millió) és a logisztikus görbe. Az adatpontok az 1815-ös, 1830-as és 1845-ös éveknek felelnek meg. A paraméterek értékei Verhulst 1845-ös cikkének értékei.
Alfred Lotka amerikai kémikus és matematikus 1907-ben kezdte el tanulmányozni a születési ráta, az életkori halálozási arányok és a népességnövekedés üteme közötti kapcsolatot integrálegyenletek segítségével. A 10. fejezetből értesülhetünk arról, hogy Lotka és Dublin vezette be a máig használatos 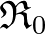 paramétert, ami Lotka modelljében az egy ember várható fiúgyermekeinek számát adja, és
paramétert, ami Lotka modelljében az egy ember várható fiúgyermekeinek számát adja, és 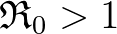 azzal ekvivalens, hogy a férfiak születési rátáját egy monoton növő exponenciális függvénnyel meg lehet adni. Számításai során rájött, hogy korfa az idők folyamán megtartja ugyanazt az alakot, de a teljes népesség exponenciálisan növekszik vagy csökken. Ezt nevezte Lotka „stabil populációnak”. Lotka termékeny kutató volt, a könyvben két fejezetet is a munkássága áttekintésének szenteltek: a 13. fejezet a jól ismert Lotka–Volterra-egyenletekkel foglalkozik. 1920-ban a matematikus felfedezte, hogy egy két biológiai fajból álló rendszer akár tartósan is oszcillálhat, tehát az exponenciális növekedés nem természetes tulajdonsága minden populációnak: míg az emberekre a járványok és az éhezés réme leselkedik, addig a növény- és állatvilág egyedeinek száma se növekedhet korlátlanul. A Lotka által vizsgált példa egy növényevő állatokból álló, növényekkel táplálkozó populáció volt. Legyen
azzal ekvivalens, hogy a férfiak születési rátáját egy monoton növő exponenciális függvénnyel meg lehet adni. Számításai során rájött, hogy korfa az idők folyamán megtartja ugyanazt az alakot, de a teljes népesség exponenciálisan növekszik vagy csökken. Ezt nevezte Lotka „stabil populációnak”. Lotka termékeny kutató volt, a könyvben két fejezetet is a munkássága áttekintésének szenteltek: a 13. fejezet a jól ismert Lotka–Volterra-egyenletekkel foglalkozik. 1920-ban a matematikus felfedezte, hogy egy két biológiai fajból álló rendszer akár tartósan is oszcillálhat, tehát az exponenciális növekedés nem természetes tulajdonsága minden populációnak: míg az emberekre a járványok és az éhezés réme leselkedik, addig a növény- és állatvilág egyedeinek száma se növekedhet korlátlanul. A Lotka által vizsgált példa egy növényevő állatokból álló, növényekkel táplálkozó populáció volt. Legyen 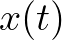 a növények össztömege és
a növények össztömege és 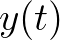 a növényevők össztömege a
a növényevők össztömege a 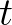 időpontban. Lotka a következő differenciálegyenlet-rendszeres modellt alkalmazta:
időpontban. Lotka a következő differenciálegyenlet-rendszeres modellt alkalmazta:
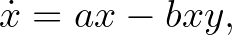
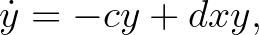
ahol az 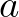 ,
, 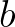 ,
,  és
és 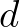 paraméterek mind pozitívak. Az
paraméterek mind pozitívak. Az 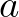 paraméter a növények növekedési rátája, ha nincsenek növényevők, míg
paraméter a növények növekedési rátája, ha nincsenek növényevők, míg  a növényevők populációjának csökkenési rátája, ha nincsenek növények. A
a növényevők populációjának csökkenési rátája, ha nincsenek növények. A 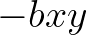 és
és 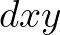 tag kifejezi, hogy minél több állat és növény van, annál nagyobb a tömegátadás a növényekből az állatok felé. Lotka észrevette, hogy két egyensúlyi helyzet van:
tag kifejezi, hogy minél több állat és növény van, annál nagyobb a tömegátadás a növényekből az állatok felé. Lotka észrevette, hogy két egyensúlyi helyzet van: 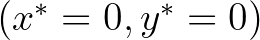 , azaz a növények és az állatok is kihaltak, illetve
, azaz a növények és az állatok is kihaltak, illetve 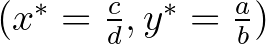 , ekkor a növények és az állatok együtt élnek, számuk nem változik. Ha a kezdeti állapot nem ezen egyensúlyi helyzetek egyike, akkor a növények és az állatok össztömege is periodikusan fog változni. Érdekesség, hogy Lotka csak egy későbbi munkájában említi meg, hogy két fajból, egy gazda- és egy parazitafajból vagy egy zsákmány- és egy ragadozófajból álló rendszerek ugyanezzel a modellel írhatók le. A fejezetben megtudhatjuk, hogy a híres matematikus, Volterra nem sokkal később egy halászati probléma tanulmányozása során Lotkától függetlenül fedezte fel ugyanezt a modellt. D'Ancona zoológus észrevette, hogy a ragadozó halak aránya megnőtt az első világháború alatt, amikor a halászat mértéke csökkent. Az észrevétel matematikai magyarázatára Volterra a fenti differenciálegyenlet-rendszert írta fel, ahol
, ekkor a növények és az állatok együtt élnek, számuk nem változik. Ha a kezdeti állapot nem ezen egyensúlyi helyzetek egyike, akkor a növények és az állatok össztömege is periodikusan fog változni. Érdekesség, hogy Lotka csak egy későbbi munkájában említi meg, hogy két fajból, egy gazda- és egy parazitafajból vagy egy zsákmány- és egy ragadozófajból álló rendszerek ugyanezzel a modellel írhatók le. A fejezetben megtudhatjuk, hogy a híres matematikus, Volterra nem sokkal később egy halászati probléma tanulmányozása során Lotkától függetlenül fedezte fel ugyanezt a modellt. D'Ancona zoológus észrevette, hogy a ragadozó halak aránya megnőtt az első világháború alatt, amikor a halászat mértéke csökkent. Az észrevétel matematikai magyarázatára Volterra a fenti differenciálegyenlet-rendszert írta fel, ahol 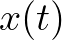 a zsákmányállatok számát,
a zsákmányállatok számát, 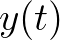 pedig a ragadozók számát jelöli. (Volterra 1926-ban jelentette meg a modellről szóló cikkét. Lotka tájékoztatta Volterrát és más tudósokat a ragadozó–zsákmány rendszerek tanulmányozásának elsőbbségéről.) Napjainkban az ilyen rendszerekre Lotka–Volterra-modellként hivatkozunk, ez az egyik legismertebb ökológiai modell.
pedig a ragadozók számát jelöli. (Volterra 1926-ban jelentette meg a modellről szóló cikkét. Lotka tájékoztatta Volterrát és más tudósokat a ragadozó–zsákmány rendszerek tanulmányozásának elsőbbségéről.) Napjainkban az ilyen rendszerekre Lotka–Volterra-modellként hivatkozunk, ez az egyik legismertebb ökológiai modell.
Leslie 1945-ben szintén egy állatpopuláció nőstényei számának növekedését vizsgálta, azonban új szemlélettel, mátrixos megfogalmazásban (21. fejezet). Legyen 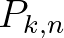 az
az 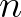 időpontban
időpontban 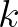 korú nőstények száma (
korú nőstények száma (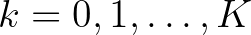 ;
; 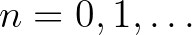 ), ahol
), ahol 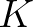 a maximális életkor, ahol még termékeny egy nőstény. Jelölje
a maximális életkor, ahol még termékeny egy nőstény. Jelölje 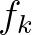 a
a 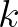 életkorúak esetén az egy nőstényre jutó leánygyermekek számát
életkorúak esetén az egy nőstényre jutó leánygyermekek számát 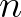 és
és 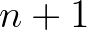 között és
között és 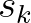 annak a valószínűségét, hogy egy
annak a valószínűségét, hogy egy 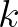 korú állat legalább
korú állat legalább 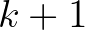 koráig életben marad. Ekkor a korstruktúrát a következő egyenletrendszerrel lehet leírni:
koráig életben marad. Ekkor a korstruktúrát a következő egyenletrendszerrel lehet leírni:
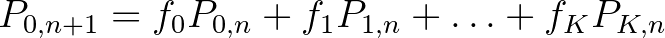
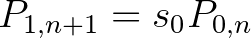
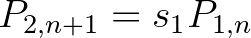
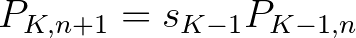
Látható, hogy a rendszer mátrixos alakban is felírható:
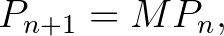
ahol 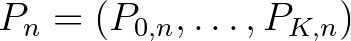 és
és 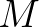 a megfelelő együtthatómátrix. Leslie a megoldást
a megfelelő együtthatómátrix. Leslie a megoldást 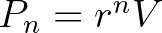 alakban kereste, így teljesülnie kell a
alakban kereste, így teljesülnie kell a 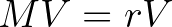 összefüggésnek. Ezek alapján Leslie rájött, hogy az
összefüggésnek. Ezek alapján Leslie rájött, hogy az 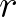 növekedési ráta egy sajátértéknek, míg a (Lotka által vett értelemben) stabil korstruktúra egy sajátvektornak felel meg. A népesség exponenciálisan növekszik pontosan akkor, ha
növekedési ráta egy sajátértéknek, míg a (Lotka által vett értelemben) stabil korstruktúra egy sajátvektornak felel meg. A népesség exponenciálisan növekszik pontosan akkor, ha 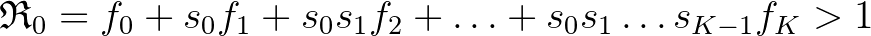 , ahol
, ahol 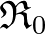 egy nőstény egyed nőstény utódainak átlagos számát fejezi ki. Ebből is jól látszik, hogy a modell Lotka munkájának egyfajta diszkrét megfelelője.
egy nőstény egyed nőstény utódainak átlagos számát fejezi ki. Ebből is jól látszik, hogy a modell Lotka munkájának egyfajta diszkrét megfelelője.
A 24. fejezetben az eddigiektől teljesen eltérő és elsőre meglepő gondolat jelenik meg: 1974-ben Robert May a diszkrét idejű logisztikus egyenletet tanulmányozása közben észrevette, hogy az egyszerű matematikai populációdinamikai modellek is kaotikusan viselkedhetnek. 1963-ban Edward Lorenz, amerikai meteorológus szintén hasonlót tapasztalt: számítógépes numerikus szimulációk segítségével megállapította, hogy a légkör mindössze három differenciálegyenletet tartalmazó egyszerűsített modellje a kezdeti feltételek apró módosítása következtében teljesen megváltoztathatja a szimuláció végeredményét. A Marylandi Egyetemen James Yorke Lorenz munkáját tanulmányozta, és ennek kapcsán bevezette a „káosz” kifejezést. 1976-ban jelent meg May cikke a témában, amelyben saját és más kutatók eredményeit is összegyűjtötte. (Magyarul: Alkalmazott Matematikai Lapok 8 (1982) 427–446.) May megmutatta, hogy a
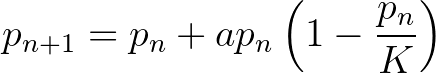
diszkrét idejű populációdinamikai modell (ahol 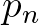 jelöli a populáció méretét az
jelöli a populáció méretét az 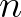 -edik évben) az
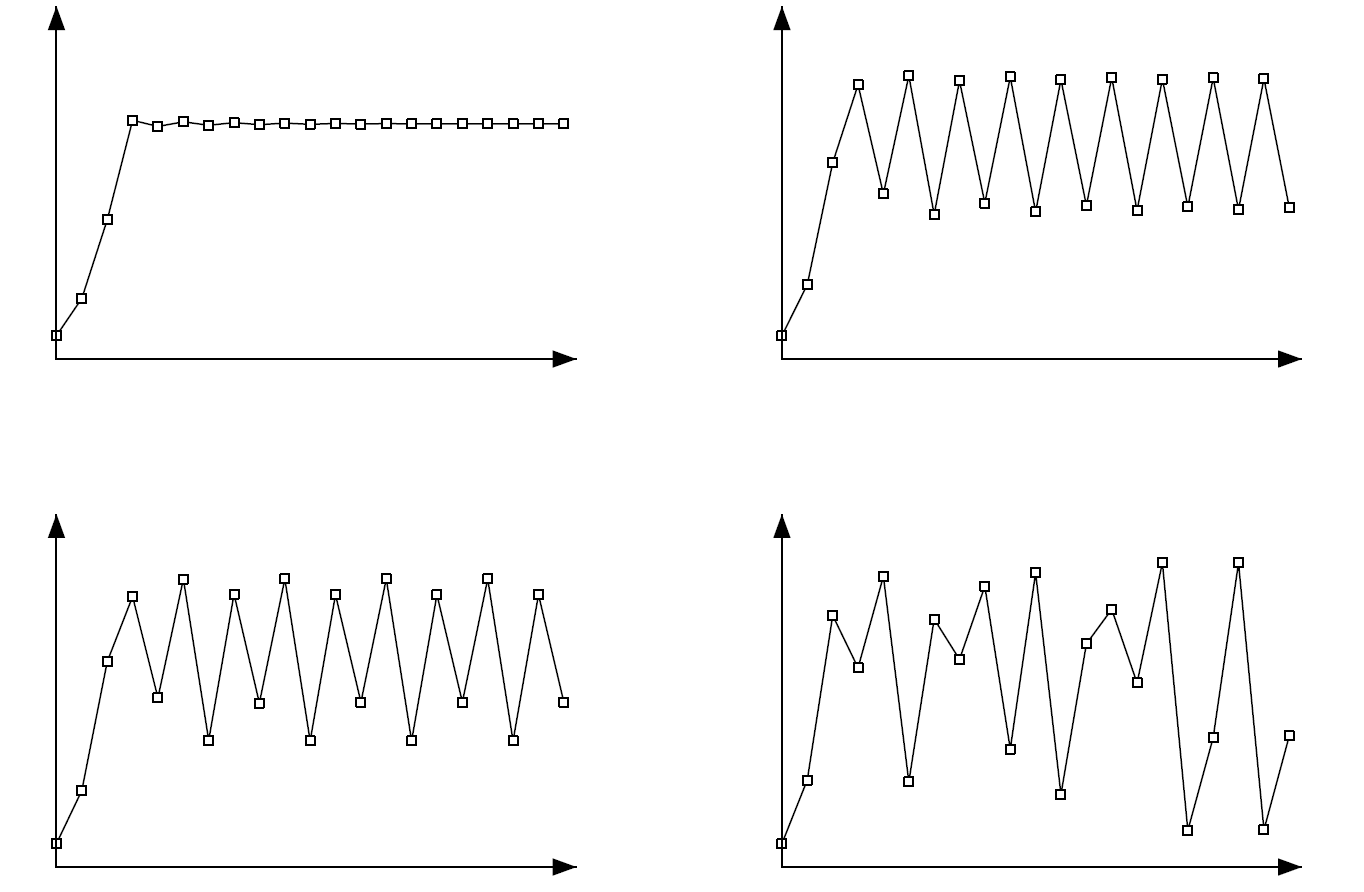
-edik évben) az 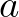 paramétertől függően teljesen más és más viselkedést mutathat (4. ábra). May cikke egyike volt azoknak, amelyek elindították a „káoszelméletet”.
paramétertől függően teljesen más és más viselkedést mutathat (4. ábra). May cikke egyike volt azoknak, amelyek elindították a „káoszelméletet”.
4. ábra. Az összes ábrán: 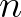 a vízszintes tengelyen,
a vízszintes tengelyen, 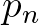 a függőleges tengelyen és
a függőleges tengelyen és 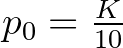 . Az egyenesek az
. Az egyenesek az 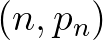 koordinátájú pontok összekötésével jönnek létre. Balra fent:
koordinátájú pontok összekötésével jönnek létre. Balra fent: 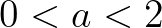 (egyensúlyi helyzet). Jobbra fent:
(egyensúlyi helyzet). Jobbra fent: 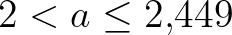 (2 periódusú ciklus). Balra lent:
(2 periódusú ciklus). Balra lent: 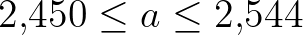 (4 periódusú ciklus). Jobbra lent:
(4 periódusú ciklus). Jobbra lent: 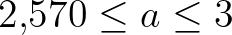 (esetleg káosz)
(esetleg káosz)
Elérkeztünk az utolsó idevágó fejezethez, ami a kínaiak egykepolitikájával foglalkozik (25. fejezet). Ez a rész bizonyos tekintetben kakukktojás az eddigiekhez képest, ugyanis a téma fő érdekessége nem a matematikai elmélet, hanem annak társadalmi hatásai. A szerzők bemutatják az ötlet 1980-as hivatalossá válásának előzményeit: hogyan vezettek egy ilyen intézkedés bevezetéséhez az irányításelmélet alkalmazásai és egy 1972-es, a gazdasági növekedés határairól szóló tanulmány? Ismertetik a Song Jian és csapata által kidolgozott matematikai modellt is: a népesség korstruktúrájának alakulását leíró parciális differenciálegyenletet (illetve annak egy diszkrét változatát), amely hozzájárult ahhoz, hogy a politikusok bevezették az egykepolitikát. Azonban még ennél is érdekesebbek ennek a politikai döntésnek a következményei, tanulságai. Talán nem is lehet találni a matematikai modellezés történetében még egy olyan esetet, amely ilyen nagy mértékben befolyásolta az emberek életét. A társadalmi „kísérlet” érdekessége, hogy a 2000-re kitűzött 1,2 milliárd fős célt nagyjából sikerült tartani, azonban a nemek aránya erősen a fiúk irányába tolódott el (a nemek alapján elvégzett abortuszok miatt). A könyv szerzői felvetik a kérdést, hogy mennyire tekinthetjük szentírásnak a matematikai modellek eredményeit? Vajon egy modell tényleg hű képet ad a valós életről? Milyen következményekkel járhat, ha egy elméletből fontos szempontokat kihagynak? Megfelelő lesz-e 2000-ben a 1,2 milliárd fős lakosság? A kínai születésszabályozás kapcsán mi olvasók is elgondolkodhatunk ezekről a kérdésekről.
3. Járványterjedés matematikája
Betegségterjedési modellekből sincs hiány a könyvben, bár sajnos nem foglalkozik olyan sok fejezet ezzel a témával, mint az előzőkkel.
Nagy örömömre szolgált, hogy az első járványterjedési modellt is ismertetik a 4. fejezetben. Daniel Bernoulli 1760-ban azt a kérdést vizsgálta, hogy a himlő elleni inokulációt ösztönözni kell-e, annak ellenére, hogy az oltás néha halálos. A ma is aktuális kérdésről Franciaországban nem foglaltak egyértelműen állast. Bernoulli matematikai modell segítségével próbálta meg összehasonlítani az inokuláció hosszútávú hasznát az azonnali halálozási kockázattal. Bevezette a ma is használt jelöléseket: legyen 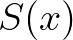 a hímlőre „fogékony” emberek száma az
a hímlőre „fogékony” emberek száma az 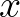 életkorban, míg
életkorban, míg 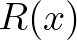 a betegséget túlélő
a betegséget túlélő 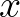 életkorú emberek száma. Ezen változókra felírt egy differenciálegyenlet-rendszert és azt különböző paraméterek mellett vizsgálta. Végül Bernoulli azt a megállapítást tette, hogy az oltás akkor előnyös, ha a halálozási kockázat kisebb, mint 11 százalék. D'Alembert bírálta Bernoulli munkáját és egy másik modellt dolgozott ki a probléma megoldására. Érdekesség, hogy Bernoulli munkáját csak később sikerült megjelentetni, míg d'Alembertnek az elméletét egyből publikálták. Bernoulli Eulernek írt levelében arra céloz, hogy ellopták az ötletét, csalódottságában fel is hagyott a populációdinamikai kérdések további vizsgálatával. Mindkét matematikus támogatta az oltást, de ennek ellenére nem vezették be azt Franciaországban. Az inokulációs dilemma akkor oldódott meg, amikor Edward Jenner 1798-ban felfedezett egy biztonságos vakcinázási módszert.
életkorú emberek száma. Ezen változókra felírt egy differenciálegyenlet-rendszert és azt különböző paraméterek mellett vizsgálta. Végül Bernoulli azt a megállapítást tette, hogy az oltás akkor előnyös, ha a halálozási kockázat kisebb, mint 11 százalék. D'Alembert bírálta Bernoulli munkáját és egy másik modellt dolgozott ki a probléma megoldására. Érdekesség, hogy Bernoulli munkáját csak később sikerült megjelentetni, míg d'Alembertnek az elméletét egyből publikálták. Bernoulli Eulernek írt levelében arra céloz, hogy ellopták az ötletét, csalódottságában fel is hagyott a populációdinamikai kérdések további vizsgálatával. Mindkét matematikus támogatta az oltást, de ennek ellenére nem vezették be azt Franciaországban. Az inokulációs dilemma akkor oldódott meg, amikor Edward Jenner 1798-ban felfedezett egy biztonságos vakcinázási módszert.
Ronald Ross orvos 1911-ben a malária terjedésének megfékezésén dolgozott (12. fejezet): a maláriával fertőzött emberek (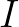 ) számára és a maláriával fertőzött szúnyogok (
) számára és a maláriával fertőzött szúnyogok (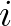 ) számára felírt két differenciálegyenletből álló rendszer segítségével azt próbálta igazolni, hogy a betegség a szúnyogok számának csökkentésével felszámolható. Megmutatta, hogy a rendszernek két egyensúlyi helyzete van, melyek közül az egyik a maláriamentes állapotnak felel meg, míg a másik egyensúlyi állapotban az
) számára felírt két differenciálegyenletből álló rendszer segítségével azt próbálta igazolni, hogy a betegség a szúnyogok számának csökkentésével felszámolható. Megmutatta, hogy a rendszernek két egyensúlyi helyzete van, melyek közül az egyik a maláriamentes állapotnak felel meg, míg a másik egyensúlyi állapotban az 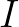 és
és 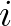 értékek pontosan akkor lesznek pozitívak (ami azt jelenti, hogy a betegség állandóan jelen van), ha a szúnyogok száma egy kritikus küszöbérték felett van. Ross ebből arra következtetett, hogy ha a szúnyogok száma e küszöbérték alá esik, akkor csak a maláriamentes egyensúlyi helyzet marad, tehát a betegség el fog tűnni. Ebben a modellben is szerepel az
értékek pontosan akkor lesznek pozitívak (ami azt jelenti, hogy a betegség állandóan jelen van), ha a szúnyogok száma egy kritikus küszöbérték felett van. Ross ebből arra következtetett, hogy ha a szúnyogok száma e küszöbérték alá esik, akkor csak a maláriamentes egyensúlyi helyzet marad, tehát a betegség el fog tűnni. Ebben a modellben is szerepel az 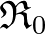 érték, ami azt méri, hogy egy fertőzött emberről átlagosan hány emberre terjed át a fertőzés (természetesen a fertőzött emberről a szúnyogokra és ezekről a szúnyogokról a többi emberre továbbfertőzve). Levezethető, hogy pontosan akkor lesz
érték, ami azt méri, hogy egy fertőzött emberről átlagosan hány emberre terjed át a fertőzés (természetesen a fertőzött emberről a szúnyogokra és ezekről a szúnyogokról a többi emberre továbbfertőzve). Levezethető, hogy pontosan akkor lesz 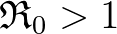 , ha a szúnyogok száma a már említett küszöbérték felett van.
, ha a szúnyogok száma a már említett küszöbérték felett van.
5. ábra. McKendrick (1876–1943) és Kermack (1898–1970)
1926-ban Anderson Gray McKendrick bevezetett egy folytonos idejű matematikai modellt járványterjedésre (16. fejezet). Egy N méretű populációban egy személy három állapotban lehet: kezdetben a fogékony 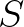 állapotban, majd a fertőzött
állapotban, majd a fertőzött 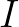 állapotban és végül a gyógyult
állapotban és végül a gyógyult 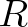 állapotban (5. ábra). Jelölje
állapotban (5. ábra). Jelölje 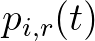 annak a valószínűségét, hogy a populációban
annak a valószínűségét, hogy a populációban 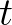 időpontban pontosan
időpontban pontosan 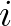 ember van az
ember van az 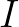 állapotban és
állapotban és 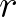 ember az
ember az 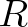 állapotban (
állapotban ( 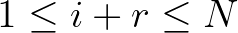 ). Ekkor ezen valószínűségekre a következő egyenletek igazak:
). Ekkor ezen valószínűségekre a következő egyenletek igazak:
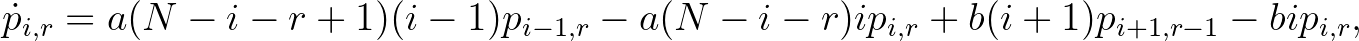
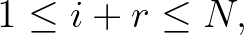
ahol 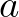 és
és 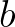 pozitív paraméterek. (A jobb oldalon szereplő első tag eltűnik, ha
pozitív paraméterek. (A jobb oldalon szereplő első tag eltűnik, ha 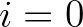 , míg a harmadik tag eltűnik
, míg a harmadik tag eltűnik 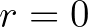 esetén. A kezdeti feltételek:
esetén. A kezdeti feltételek: 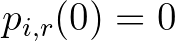 minden
minden 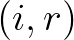 mellett, kivéve, hogy
mellett, kivéve, hogy 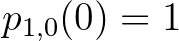 .) McKendrick kiszámította a
.) McKendrick kiszámította a 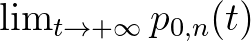 határértéket, ami megadja annak a valószínűségét, hogy a járvány
határértéket, ami megadja annak a valószínűségét, hogy a járvány 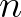 embert fertőz meg. Érdekesség, hogy ez a valószínűség a fenti rendszer megoldása nélkül is kiszámítható, az ötletet az érdeklődők elolvashatják a könyvben. Willaim Ogilvy Kermack 1927-től együtt kutatott McKendrickkel, az ő nevükhöz fűződik a klasszikus három differenciálegyenletből álló SIR modell:
embert fertőz meg. Érdekesség, hogy ez a valószínűség a fenti rendszer megoldása nélkül is kiszámítható, az ötletet az érdeklődők elolvashatják a könyvben. Willaim Ogilvy Kermack 1927-től együtt kutatott McKendrickkel, az ő nevükhöz fűződik a klasszikus három differenciálegyenletből álló SIR modell:
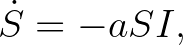
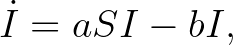
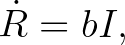
ahol 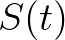 ,
, 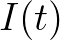 ,
, 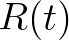 jelöli rendre a fogékony, a beteg és a gyógyult emberek számát a
jelöli rendre a fogékony, a beteg és a gyógyult emberek számát a 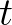 időpontban,
időpontban, 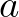 a fertőződési, míg
a fertőződési, míg 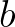 a gyógyulási ráta. A rendszer ebben a formában nem megoldható, de több tulajdonságát már akkor is ismerték:
a gyógyulási ráta. A rendszer ebben a formában nem megoldható, de több tulajdonságát már akkor is ismerték:

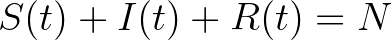 minden
minden 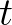 -re,
-re,

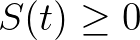 ,
, 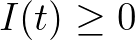 ,
, 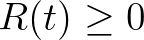 minden
minden 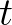 -re,
-re,

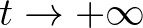 esetén
esetén 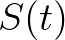 monoton fogyólag tart az
monoton fogyólag tart az 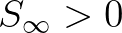 értékhez,
értékhez, 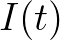 tart 0-hoz és
tart 0-hoz és 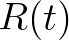 monoton növőleg tart az
monoton növőleg tart az  értékhez,
értékhez,
 fennáll a következő összefüggés:
fennáll a következő összefüggés:
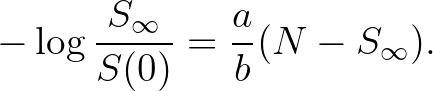
A kutatók ehhez a modellhez is meg tudtak adni egy 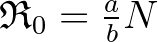 értéket, ami azt méri hogy egy, a járvány kezdetén megfertőzött személy átlagosan hány személyt fertőz meg. McKendrickék érvei alapján a járvány pontosan akkor fertőzi meg a népesség jelentős részét, ha
értéket, ami azt méri hogy egy, a járvány kezdetén megfertőzött személy átlagosan hány személyt fertőz meg. McKendrickék érvei alapján a járvány pontosan akkor fertőzi meg a népesség jelentős részét, ha 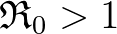 . Ez azt is jelenti, hogy ha a népesség kisebb mint
. Ez azt is jelenti, hogy ha a népesség kisebb mint 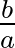 , akkor nem alakul ki járvány. Manapság az
, akkor nem alakul ki járvány. Manapság az 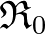 paraméter reprodukciós számként ismert, és a legtöbb modellben részletesen foglalkoznak a meghatározásával. Kermack és McKendrick az 1930-as években több járványmodellt is kidolgozott, amelyek a mai elméletek alapjai.
paraméter reprodukciós számként ismert, és a legtöbb modellben részletesen foglalkoznak a meghatározásával. Kermack és McKendrick az 1930-as években több járványmodellt is kidolgozott, amelyek a mai elméletek alapjai.
Az utolsó járványterjedéssel kapcsolatos modellről a 22. fejezetben olvashatunk. John Michael Hammersley és Simon Ralph Broadbent 1957-es munkája a perkolációelmélet kiindulópontja. Egyik példájuk egy járvány terjedése egy gyümölcsösben, a kérdés a következő: egy négyzet alakú hálózat csomópontjaiban elhelyezett fák milyen valószínűséggel adják tovább szomszédaiknak a fertőzést, hogy a beteg fák száma végtelen legyen. Először csak elméleti úton vizsgálták a problémát, azonban az 1970-es években a modern számítógépek fejlődésével már szimulációkat is futtattak. Tapsztalataikat az 1964-es Monte Carlo módszerek című könyvben ismertette Hammersley David Handscomb-mal közösen.
A könyvben bemutatott modellek nagyon hasonlóak a napjainkban használtakhoz, a járványtani modellek alapköveinek tekinthetők. Számomra nagyon érdekes volt végigolvasni, hogy a matematikusok és a kutatók milyen számítási módszereket alkalmaztak egy-két évszázaddal ezelőtt. Meglepően sok információt meg tudtak állapítani a modellekről a modern számítógépek nélkül is, amelyek manapság elengedhetetlen kellékei a járványterjedési modellezésnek.
adjunktus
BME Analízis Tanszék