Statisztikus tanuláselmélet: Szupport vektor gépek
1. Bevezető
A mesterséges intelligencia (MI) technológiák ma már a mindennapjaink részét képezik, számos szolgáltatás alapjául szolgálnak – az egészségügytől az iparig –, és a gazdasági fejlődés egyik lehetséges motorjai, állapítja meg egy az MI-t az Európai Unió (EU) szemszögéből vizsgáló tanulmány [4]. Az MI fogalmának meghatározására sokfajta megközelítés létezik [3], de abban szinte minden kutató egyetért, hogy a gépi tanulás a terület kulcsfontosságú módszere, amely a legtöbb MI megoldás esszenciális részét képezi [4].
A gépi tanulás matematikai megalapozása rendkívül fontos a terület hosszútávú fejlődése szempontjából. Noha sok heurisztikus megoldást is használnak a gyakorlatban, a gépi tanulás elmélete mostanra gazdag múlttal rendelkezik, amelynek fontos része a statisztikus tanuláselmélet. Tanulmányunk első részében a statisztikus tanuláselmélet egyik klasszikus módszerébe, a szupport vektor gépek elméletébe adunk bevezetést, a gépi tanulás egyik alapproblémáján, a (bináris) osztályozáson keresztül. A megoldást első lépésként lineárisan szeparálható problémák esetére vezetjük be, amit a tanulmányunk folytatásában kernel módszerek segítségével terjesztünk majd ki nemlineáris problémákra.
2. Bináris osztályozás
Az osztályozás (más néven klasszifikáció vagy mintafelismerés) a statisztikus tanuláselmélet egyik alapvető problémája. Fő feladata bemenet és (véges értékkészletű) kimenet (címke) párokból álló megfigyelések alapján az adatgeneráló mechanizmus modellezése. A modell segíségével általánosíthatunk, azaz ismeretlen bemenetek esetén is becsülni tudjuk a megfelelő kimenetet. Egy osztályozási feladat bináris, ha a címke csak kétféle lehet.
Az osztályozásnak számtalan alkalmazása van, amelyek közül most hármat említünk. Tanulmányunk során az első példán keresztül szemléltetünk majd néhány alapfogalmat.
Betegség diagnosztizálása: Az egészségügyben az orvos feladata, hogy diagnosztizáljon egy adott betegséget a páciens tünetei és leletei alapján. Ez egy tipikus osztályozási feladat, amely során a cél a betegség meglétének eldöntése a rendelkezésére álló adatok (magyarázóváltozók) alapján (például: nem, kor, súly, vérnyomás, pulzus, EKG, CT).
Szerszámgép karbantartása: Annak érdekében, hogy a szerszámgépek váratlan meghibásodásának számát csökkentsék, a gépek részegységeinek állapotát rendeszeresen mérik. A meghibásodás előrejelzése a mért értékek alapján egy osztályozási feladat, amely megoldása elengedhetetlen hatékony karbantartási stratégiák kialakításához.
Levélszemét (spam) felismerése: A levelezőrendszerek a bejövő üzeneteket számos tényező (például: szöveges tartalom, címzettek, csatolmányok, linkek, a rendszer címjegyzéke, a feladó címéről feladott levelek száma és hasonlósága) alapján osztályozzák, hogy a veszélyes és nem kívánt emailek elkülönüljenek a levelezőkliens beérkező leveleitől.
Adott egy vektor magyarázó változókból, 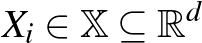 , és bináris osztályváltozókból,
, és bináris osztályváltozókból, 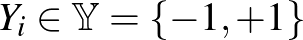 , álló független azonos eloszlású minta
, álló független azonos eloszlású minta 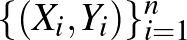 egy ismeretlen
egy ismeretlen 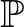 eloszlásból. Tekintsük az
eloszlásból. Tekintsük az 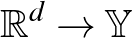 típusú (mérhető) osztályozó függvényeket és egy (mérhető) nemnegatív
típusú (mérhető) osztályozó függvényeket és egy (mérhető) nemnegatív 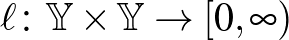 típusú veszteségfüggvényt. Ebben a cikkben az
típusú veszteségfüggvényt. Ebben a cikkben az 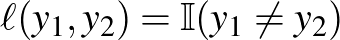 ún.
ún.  -veszteségfüggvényre szorítkozunk, ahol
-veszteségfüggvényre szorítkozunk, ahol 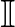 egy indikátor, de az eredmények általánosíthatóak más, bonyolultabb veszteségfüggvényekre is. Általában az osztályozás célja egy minimális kockázatú osztályozó
egy indikátor, de az eredmények általánosíthatóak más, bonyolultabb veszteségfüggvényekre is. Általában az osztályozás célja egy minimális kockázatú osztályozó 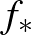 becslése, ahol
becslése, ahol
![$\displaystyle R(f) \doteq \mathbb{E}\big[\ell(f(X), Y)\big],
$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img11.png)
az ún. kockázatfüggvény és 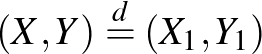 . A
. A 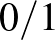 -veszteségfüggvény esetén könnyen látható, hogy
-veszteségfüggvény esetén könnyen látható, hogy 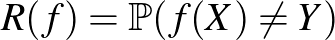 , azaz a kockázat megegyezik a félreosztályozás valószínűségével. Ha
, azaz a kockázat megegyezik a félreosztályozás valószínűségével. Ha 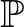 ismert volna, akkor egy optimális osztályozó – az ún. Bayes optimális osztályozó – meghatározható lenne a feltételes várható érték segítségével:
ismert volna, akkor egy optimális osztályozó – az ún. Bayes optimális osztályozó – meghatározható lenne a feltételes várható érték segítségével:
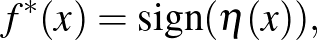
ahol ![$\eta(x) \doteq \mathbb{E}[Y\vert X=x]$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img15.png) , amit tipikusan regressziós függgvénynek neveznek. Az egészségügyi példában a már megfigyelt páciensek egészségügyi adatai (nem, kor, EKG...) alkotják a magyarázó változókat és egy adott betegség előfordulásának indikátorai a kimeneti változókat. Feltehető, hogy ezek az adatok egy euklideszi térbe ágyazhatók be, ugyanis a megfigyelések egy része euklideszi térből vesz fel értéket, a magyarázó változók további része pedig vektorrá transzformálható valamilyen módon, például segéd indikátorváltozók bevezetésével. Egy leegyszerűsített modellben az ismeretlen eloszlást minden ember egészségügyi adata és betegsége határozná meg. Ha a
, amit tipikusan regressziós függgvénynek neveznek. Az egészségügyi példában a már megfigyelt páciensek egészségügyi adatai (nem, kor, EKG...) alkotják a magyarázó változókat és egy adott betegség előfordulásának indikátorai a kimeneti változókat. Feltehető, hogy ezek az adatok egy euklideszi térbe ágyazhatók be, ugyanis a megfigyelések egy része euklideszi térből vesz fel értéket, a magyarázó változók további része pedig vektorrá transzformálható valamilyen módon, például segéd indikátorváltozók bevezetésével. Egy leegyszerűsített modellben az ismeretlen eloszlást minden ember egészségügyi adata és betegsége határozná meg. Ha a 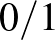 veszteségfüggvényt használjuk és az ehhez tartozó kockázatot, azaz a betegségek félrediagnosztizálásanak valószínűségét szeretnénk minimalizálni, akkor egy Bayes optimális osztályozó pontosan akkor diagnosztizál egy pácienst betegnek, ha a betegség feltételes valószínűsége a páciens egészségügyi adataira nézve nagyobb, mint annak a valószínűsége, hogy a páciens egészséges. Ezt az optimális függvényt becsüljük az osztályozáskor a megfigyelt adatok alapján.
veszteségfüggvényt használjuk és az ehhez tartozó kockázatot, azaz a betegségek félrediagnosztizálásanak valószínűségét szeretnénk minimalizálni, akkor egy Bayes optimális osztályozó pontosan akkor diagnosztizál egy pácienst betegnek, ha a betegség feltételes valószínűsége a páciens egészségügyi adataira nézve nagyobb, mint annak a valószínűsége, hogy a páciens egészséges. Ezt az optimális függvényt becsüljük az osztályozáskor a megfigyelt adatok alapján.
A 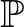 együttes eloszlás általában ismeretlen, ezért a kockázatfüggvényt becsülnünk kell. A legismertebb becslés az ún. tapasztalati kockázat, a megfigyelt veszteségek átlaga:
együttes eloszlás általában ismeretlen, ezért a kockázatfüggvényt becsülnünk kell. A legismertebb becslés az ún. tapasztalati kockázat, a megfigyelt veszteségek átlaga:
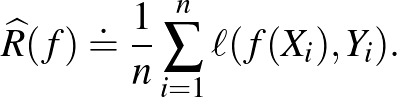
A nagy számok (erős) törvényének értelmében minden  osztályozóra
osztályozóra  konvergál az
konvergál az 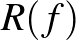 értékhez,
értékhez, 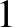 valószínűséggel. A tapasztalati kockázat minimalizálásának módszere értelemszerűen az
valószínűséggel. A tapasztalati kockázat minimalizálásának módszere értelemszerűen az  függvény minimumhelyét keresi. Általában azonban minden
függvény minimumhelyét keresi. Általában azonban minden 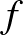 osztályozóhoz található egy
osztályozóhoz található egy 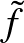 osztályozó, ami a mintapontokban megegyezik
osztályozó, ami a mintapontokban megegyezik 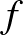 -fel, azaz
-fel, azaz 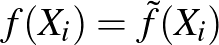 minden
minden 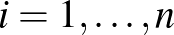 , de mindenhol máshol
, de mindenhol máshol 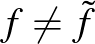 , ezért önmagában a minta alapján nem lehet egyértelműen meghatározni a tapasztalati kockázatot minimalizáló osztályozót. Általában a tapasztalati kockázatminimalizálás esetében egy előre rögzített modellosztályra szorítkozunk. A modellosztályt gyakran egy véges dimenziós paramétervektor segítségével adjuk meg. Példaként tekinthetjük a lineáris (pontosabban az affin) osztályozókat, melyeket szeparáló hipersíkok definiálnak:
, ezért önmagában a minta alapján nem lehet egyértelműen meghatározni a tapasztalati kockázatot minimalizáló osztályozót. Általában a tapasztalati kockázatminimalizálás esetében egy előre rögzített modellosztályra szorítkozunk. A modellosztályt gyakran egy véges dimenziós paramétervektor segítségével adjuk meg. Példaként tekinthetjük a lineáris (pontosabban az affin) osztályozókat, melyeket szeparáló hipersíkok definiálnak: 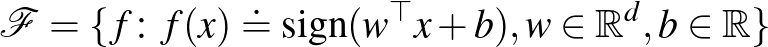 .
.
Legyen 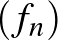 a Bayes optimális osztályozó egy becslése (ahol
a Bayes optimális osztályozó egy becslése (ahol 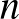 a megfigyelések száma). Azt mondjuk, hogy az
a megfigyelések száma). Azt mondjuk, hogy az 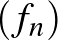 becslés (erősen) konzisztens, ha
becslés (erősen) konzisztens, ha  , ahogy
, ahogy  ,
, 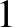 valószínűséggel (mivel
valószínűséggel (mivel 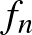 függ a megfigyelésektől, ezért
függ a megfigyelésektől, ezért 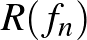 véletlen).
véletlen).
Ismeretlen eloszlás mellett adott mintaméretre hatékony osztályozót nehéz találni, az ún. „nincs ingyen ebéd” elve érvényesül [2, Theorem 7.1]:
1. tétel. Legyen 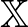 egy végtelen halmaz. Ekkor minden
egy végtelen halmaz. Ekkor minden 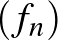 becsléshez,
becsléshez, 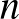 mintamérethez és
mintamérethez és 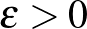 hibavalószínűséghez létezik egy
hibavalószínűséghez létezik egy 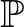 eloszlás, amelyre
eloszlás, amelyre 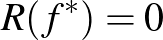 és
és ![$\mathbb{E}[R(f_n)] \geq 1/2-\varepsilon$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img36.png) .
.
Ha a megfigyelésektől teljesen függetlenül, véletlenszerűen (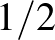 -
- 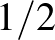 valószínűséggel) rendelnénk minden ponthoz egy osztályt, akkor lenne
valószínűséggel) rendelnénk minden ponthoz egy osztályt, akkor lenne 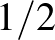 az osztályozónk kockázata. A fenti tétel azt mondja, hogy egy adott becsléshez tudunk olyan „rossz” eloszlást konstruálni, amelyre a becslésünk kockázata tetszőlegesen közel lehet ehhez a teljesen véletlenített osztályozóhoz, noha van az adott problémára tökéletes, nulla kockázatú megoldás.
az osztályozónk kockázata. A fenti tétel azt mondja, hogy egy adott becsléshez tudunk olyan „rossz” eloszlást konstruálni, amelyre a becslésünk kockázata tetszőlegesen közel lehet ehhez a teljesen véletlenített osztályozóhoz, noha van az adott problémára tökéletes, nulla kockázatú megoldás.
Megjegyezzük, hogy ez a tétel nem jelenti azt, hogy lehetetlen olyan becslést találni, amely univerzálisan minden eloszlásra konzisztens lenne, azaz  teljesülne. Azt viszont igen, hogy a konzisztens becslések esetében is a konvergencia sebessége az eloszlás függvényében változik és lehet tetszőlegesen lassú. Egy meglepően egyszerű univerzálisan konzisztens módszert ad a
teljesülne. Azt viszont igen, hogy a konzisztens becslések esetében is a konvergencia sebessége az eloszlás függvényében változik és lehet tetszőlegesen lassú. Egy meglepően egyszerű univerzálisan konzisztens módszert ad a  -legközelebbi szomszéd (
-legközelebbi szomszéd ( -NN) becslés. Jelölje
-NN) becslés. Jelölje
![$\displaystyle N_k(x) \doteq \Big\{ j \in[n] \colon \sum_{i=1}^n \mathbb{I}(\lVert x- X_j\rVert > \lVert x-X_i\rVert)< k \Big\},
$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img39.png)
ahol ![$[n] \doteq \{1, 2, \dots, n\}$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img40.png) . Tehát egy tetszőleges
. Tehát egy tetszőleges 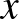 pont esetén az
pont esetén az 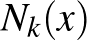 halmaz a
halmaz a  halmazban az
halmazban az 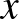 pont
pont  legközelebbi szomszédainak indexeit tartalmazza. Továbbá legyen
legközelebbi szomszédainak indexeit tartalmazza. Továbbá legyen
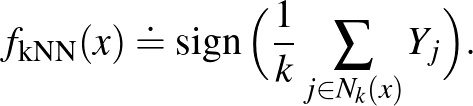
A szomszédok számát a minta elemszámának függvényében növelhetjük, hogy egy konzisztens becslést kapjunk. Ha a 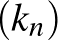 sorozat olyan, hogy
sorozat olyan, hogy  és
és 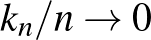 , ha
, ha  akkor a
akkor a 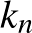 -NN becslés kockázata tart az optimális
-NN becslés kockázata tart az optimális 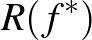 kockázat értékhez [2].
kockázat értékhez [2].
Az 1. Tétel miatt azonban nem várható el, hogy egy tetszőleges eloszlásból vett véges mintára is mindig használható becslést kapjunk, ezért érdemes megkötésekkel élnünk a lehetséges modelleket illetően. Általában a becslést egy 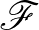 modellosztályban fogjuk keresni. Mivel a tapasztalati kockázatminimalizálás már előfeltételezi egy modellosztály létezését, ezért ez a feltevés a gyakorlatban alapvető, mindazonáltal érdemes észben tartani, hogy ennek a feltevésnek lehet torzító hatása. Ezt nevezik a feladatban rejlő induktív torzításnak. Egy
modellosztályban fogjuk keresni. Mivel a tapasztalati kockázatminimalizálás már előfeltételezi egy modellosztály létezését, ezért ez a feltevés a gyakorlatban alapvető, mindazonáltal érdemes észben tartani, hogy ennek a feltevésnek lehet torzító hatása. Ezt nevezik a feladatban rejlő induktív torzításnak. Egy 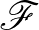 -ből származó becslés kockázattöbbletét felbonthatjuk két részre.
-ből származó becslés kockázattöbbletét felbonthatjuk két részre.
Ha 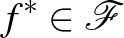 , akkor az approximációs hiba 0, azonban ez elég ritkán teljesül a gyakorlatban. Ha bővítjük a modellosztályt, akkor az approximációs hiba csökken, viszont a becslési hiba növekedhet. A túl nagy modellosztály eredményezhet túltanulást, ilyenkor a modellbecslés a mintában lévő zajra is illeszkedik. Megfordítva, ha túl szűk modellosztályt választunk, akkor a becslési hibánk lecsökken, nem lesz nagy különbség a modellosztályban található legkisebb kockázatú becslés kockázata és az általunk talált becslés kockázata között, azonban az approximációs hiba ilyenkor megnő. Ezt a szintén nem előnyös jelenségét alultanulásnak nevezik. Ha növeljük a mintaméretet, akkor a becslési hibát tudjuk csökkenteni, viszont az approximációs tag csak a modellosztálytól függ.
, akkor az approximációs hiba 0, azonban ez elég ritkán teljesül a gyakorlatban. Ha bővítjük a modellosztályt, akkor az approximációs hiba csökken, viszont a becslési hiba növekedhet. A túl nagy modellosztály eredményezhet túltanulást, ilyenkor a modellbecslés a mintában lévő zajra is illeszkedik. Megfordítva, ha túl szűk modellosztályt választunk, akkor a becslési hibánk lecsökken, nem lesz nagy különbség a modellosztályban található legkisebb kockázatú becslés kockázata és az általunk talált becslés kockázata között, azonban az approximációs hiba ilyenkor megnő. Ezt a szintén nem előnyös jelenségét alultanulásnak nevezik. Ha növeljük a mintaméretet, akkor a becslési hibát tudjuk csökkenteni, viszont az approximációs tag csak a modellosztálytól függ.
A strukturális kockázatminimalizálás elve szerint érdemes a modellosztályt úgy bővíteni a mintamérettel együtt, hogy a becslési hiba és az approximációs hiba is csökkenjen, lásd az 1. ábrát. Az approximációs hiba modellosztálytól való függésére több „mérőszámot” is megalkottak. Ezek a mérőszámok elsősorban a modellosztály kifejezőképességét hívatottak leírni. Ebben a cikkben az ún. Vapnik–Cservonenkisz-dimenziót (VC-dimenziót) mutatjuk be és ennek alkalmazását a bináris osztályozás esetére, lásd [7].
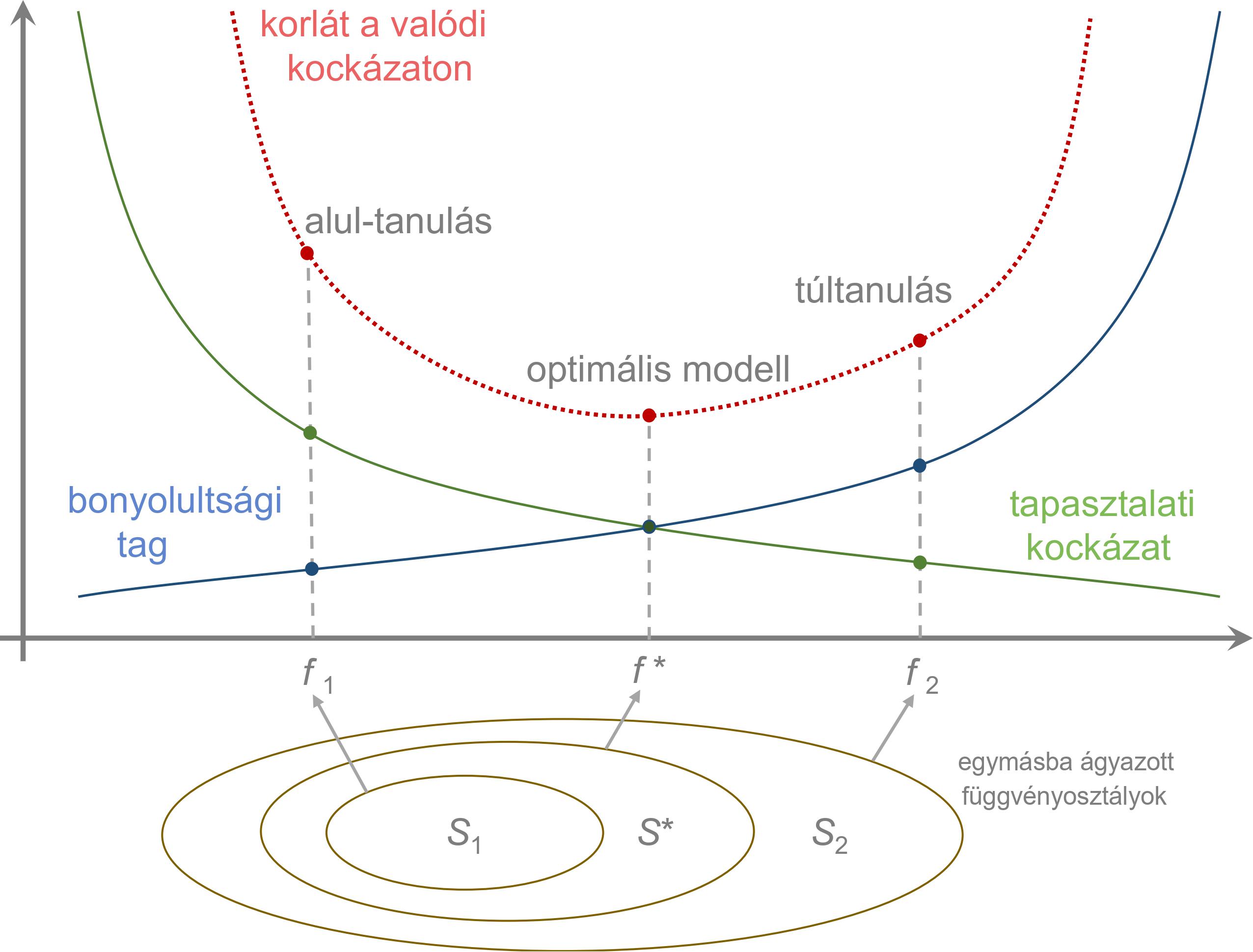
1. ábra. Torzítás-variancia dilemma, strukturális kockázatminimalizálás
Legyen 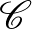 egy halmazrendszer. Azt mondjuk, hogy
egy halmazrendszer. Azt mondjuk, hogy 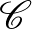 szétzúzza az
szétzúzza az 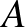 halmazt, ha
halmazt, ha
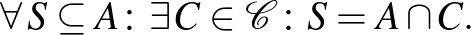
Hasonlóan, bináris osztályozók egy 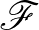 osztálya szétzúzza az
osztálya szétzúzza az 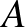 halmazt, ha az osztályozók által generált
halmazt, ha az osztályozók által generált 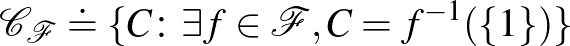 halmazrendszer szétzúzza
halmazrendszer szétzúzza 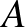 -t.
-t.
2. definíció. (VC-dimenzió) Legyen 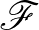 osztályozóknak egy családja. Az
osztályozóknak egy családja. Az 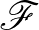 halmaz
halmaz 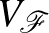 VC-dimenziója az a legnagyobb
VC-dimenziója az a legnagyobb 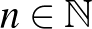 , amire létezik egy
, amire létezik egy 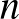 -elemű
-elemű 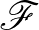 által szétzúzott
által szétzúzott 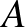 halmaz. Ha ez a maximum nem létezik, akkor
halmaz. Ha ez a maximum nem létezik, akkor 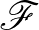 VC-dimenziója végtelen.
VC-dimenziója végtelen.
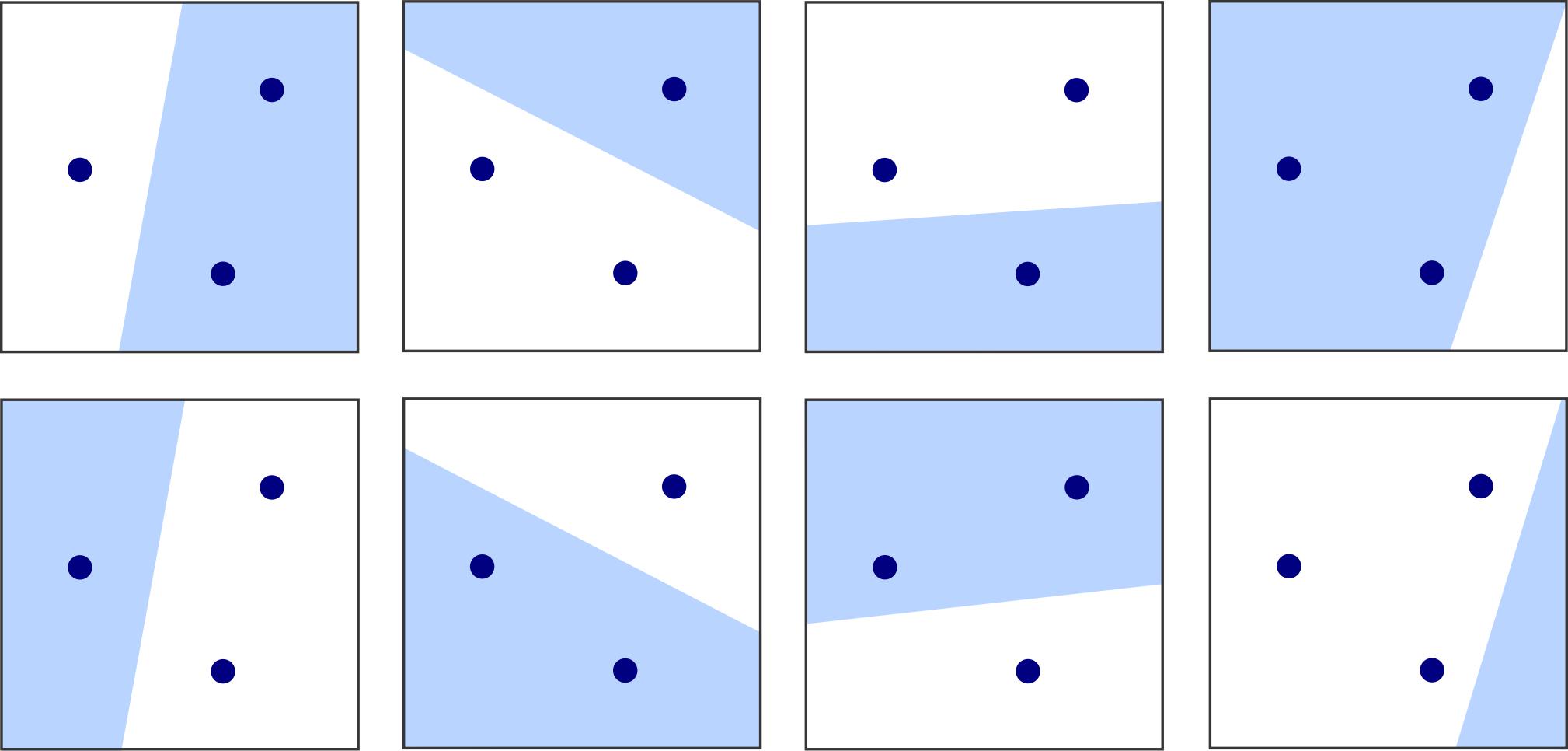
2. ábra. Lineáris osztályozók szétzúznak egy 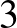 elemű halmazt
elemű halmazt 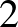 dimenzióban
dimenzióban
Megmutatható, hogy a lineáris osztályozók VC-dimenziója az 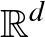 térben
térben 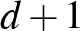 (lásd 2. ábra). A tetszőlegesen nagy fokú polinomok által generált osztályozók VC-dimenziója pedig végtelen. A VC-dimenzió segítségével jól bemutatható a strukturális kockázatminimalizálás. Legyen
(lásd 2. ábra). A tetszőlegesen nagy fokú polinomok által generált osztályozók VC-dimenziója pedig végtelen. A VC-dimenzió segítségével jól bemutatható a strukturális kockázatminimalizálás. Legyen ![$\ell\colon \mathbb{Y} \to \mathbb{Y} \to [0, \beta]$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img64.png) egy korlátos veszteségfüggvény,
egy korlátos veszteségfüggvény, 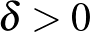 és
és

Ekkor megmutatható, hogy
Az ilyen típusú korlátokat nagy valószínűséggel megközelítőleg helyes – angol nevéből PAC – korlátoknak nevezik. A PAC korlátok nagyon elterjedtek a gépi tanulásban, és a gyakorlatban is jól használhatók. Fontos előnyük, hogy véges mintára is érvényes garanciával szolgálnak. Az (1) egyenlőtlenség alapján érdemes az 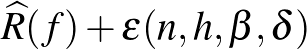 tagot együttesen minimalizálni a tapasztalati kockázat helyett. Legyen
tagot együttesen minimalizálni a tapasztalati kockázat helyett. Legyen 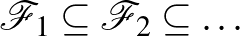 modellosztályoknak egy bővülő sorozata. Természetesen ekkor a modellosztályok VC-dimenziója is monoton növő. A strukturális kockázatminimalizálás során azt a modellosztályt és azon belül azt a modellt keressük, amelyre a fenti együttes hibatag minimális.
modellosztályoknak egy bővülő sorozata. Természetesen ekkor a modellosztályok VC-dimenziója is monoton növő. A strukturális kockázatminimalizálás során azt a modellosztályt és azon belül azt a modellt keressük, amelyre a fenti együttes hibatag minimális.
3. Szupport vektor gépek
Fontos példaként vizsgáljuk meg a lineáris osztályozóknak egy paraméteres részhalmazát: a 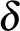 -margójú szeparáló hipersíkokat. Legyenek
-margójú szeparáló hipersíkokat. Legyenek  tetszőleges pontok
tetszőleges pontok 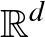 -ben egy
-ben egy  sugarú origó középpontú gömbben. Tekintsük az
sugarú origó középpontú gömbben. Tekintsük az
![$\displaystyle \mathcal{F}_\delta(\mathcal{X}) \doteq \big\{ f(x) = \mathop{\mat...
...k \in[r]} \vert w^{\top} x_k + b\vert =1, \lVert w\rVert \leq 1/\delta \big\}.
$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img73.png)
modellosztályt, amely az 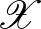 -beli pontoktól legalább
-beli pontoktól legalább 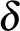 távolságra lévő egyenesek által meghatározott osztályozókat tartalmazza. A
távolságra lévő egyenesek által meghatározott osztályozókat tartalmazza. A ![$\min_{k \in[r]}\vert w^{\top} x_k + b\vert =1$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img75.png) kitétel egyértelműsíti a hipersíkok paraméterezését, a statisztikus tanuláselméletben ezt a paraméterezést szokás kanonikus paraméterezésnek nevezni (tehát itt
kitétel egyértelműsíti a hipersíkok paraméterezését, a statisztikus tanuláselméletben ezt a paraméterezést szokás kanonikus paraméterezésnek nevezni (tehát itt 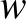 tipikusan nem egységvektor). Az
tipikusan nem egységvektor). Az 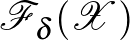 halmaz VC-dimenziójára adható egy felső korlát a
halmaz VC-dimenziójára adható egy felső korlát a 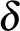 függvényében [5,6].
függvényében [5,6].
3. tétel. Legyen 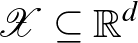 egy véges halmaz. Tegyük fel, hogy
egy véges halmaz. Tegyük fel, hogy 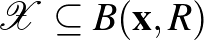 egy valamilyen
egy valamilyen 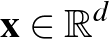 elemre. Tekintsük az
elemre. Tekintsük az 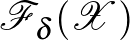 osztályozókat az
osztályozókat az 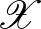 halmazon. Ekkor
halmazon. Ekkor
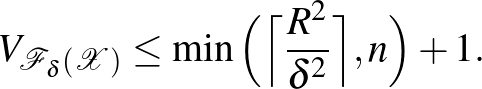
Ez az állítás motiválja, hogy érdemes a margót növelni, ha a függvényosztály komplexitását csökkenteni szeretnénk. Megjegyezzük azonban, hogy az (1) egyenletben szereplő korlát csak akkor érvényes, ha a strukturális kockázat minimalizálásban szereplő függvényosztályok nem függnek a mintától [6].
Vizsgáljuk meg azt az esetet, amikor az osztályok lineárisan szeparálhatók, azaz 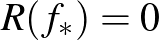 . Ilyenkor mindig található egy olyan lineáris osztályozó is, aminek a tapasztalati hibája 0. Egy optimalizálási feladat segítségével megkereshető a maximális margójú hipersík is. Belátható, hogy ez egyértelműen létezik.
. Ilyenkor mindig található egy olyan lineáris osztályozó is, aminek a tapasztalati hibája 0. Egy optimalizálási feladat segítségével megkereshető a maximális margójú hipersík is. Belátható, hogy ez egyértelműen létezik.
Egy 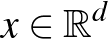 pont algebrai távolsága egy
pont algebrai távolsága egy  paraméterekkel meghatározott hipersíktól az
paraméterekkel meghatározott hipersíktól az  valós szám, ha
valós szám, ha 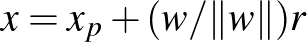 fennáll egy
fennáll egy 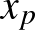 hipersíkon lévő pontra, azaz
hipersíkon lévő pontra, azaz 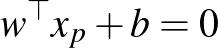 . Az algebrai távolság a kanonikus paraméterezés mellett fordítottan arányos a
. Az algebrai távolság a kanonikus paraméterezés mellett fordítottan arányos a 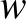 vektor normájával, ugyanis
vektor normájával, ugyanis
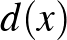 |
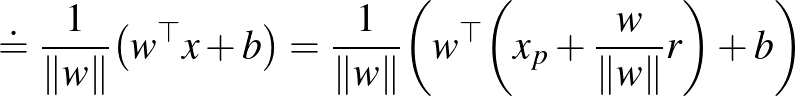 |
 |
Az  pont euklideszi távolsága a
pont euklideszi távolsága a  által meghatározott egyenestől (hipersíktól) értelemszerűen
által meghatározott egyenestől (hipersíktól) értelemszerűen 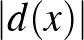 . A hipersík margója a mintákra nézve
. A hipersík margója a mintákra nézve ![$\delta_* \doteq \min_{k \in [n]} \vert d(x_k)\vert$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img93.png) . Azokat az
. Azokat az 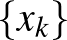 magyarázóvektorokat, amelyekre
magyarázóvektorokat, amelyekre 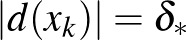 , szupport vektoroknak nevezzük. Belátható, hogy ugyanezekre a vektorokra teljesül a
, szupport vektoroknak nevezzük. Belátható, hogy ugyanezekre a vektorokra teljesül a 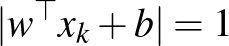 egyenlőség. Ezen meggondolások alapján a
egyenlőség. Ezen meggondolások alapján a 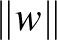 mennyiséget kell maximalizálni a kanonikus paraméterezés által meghatározott peremfeltételek mellett, lásd a 3. ábrát. Evvel ekvivalens módon az alábbi konvex kvadratikus optimalizálási problémát kell megoldanunk:
mennyiséget kell maximalizálni a kanonikus paraméterezés által meghatározott peremfeltételek mellett, lásd a 3. ábrát. Evvel ekvivalens módon az alábbi konvex kvadratikus optimalizálási problémát kell megoldanunk:
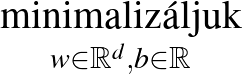 |
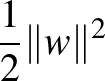 |
|
| feltéve, hogy |  |
minden 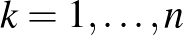 |
A nemlineáris optimalizálás elméletéből ismert Karush–Kuhn–Tucker-feltételek [1] alapján belátható, hogy az optimális 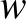 megoldáshoz legalább két szupport vektor,
megoldáshoz legalább két szupport vektor,  és
és 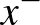 , tartozik, ugyanis ellenkező esetben a margót növelni lehetne. Ezekre a vektorokra teljesülnek a
, tartozik, ugyanis ellenkező esetben a margót növelni lehetne. Ezekre a vektorokra teljesülnek a  egyenletek, amelyek segítségével az optimális
egyenletek, amelyek segítségével az optimális 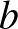 paraméter is meghatározható. Ezt a módszert a szigorú margójú szupport vektor gépek módszerének nevezzük, és az így kapott osztályozót (lineáris) szupport vektor osztályozónak hívjuk.
paraméter is meghatározható. Ezt a módszert a szigorú margójú szupport vektor gépek módszerének nevezzük, és az így kapott osztályozót (lineáris) szupport vektor osztályozónak hívjuk.
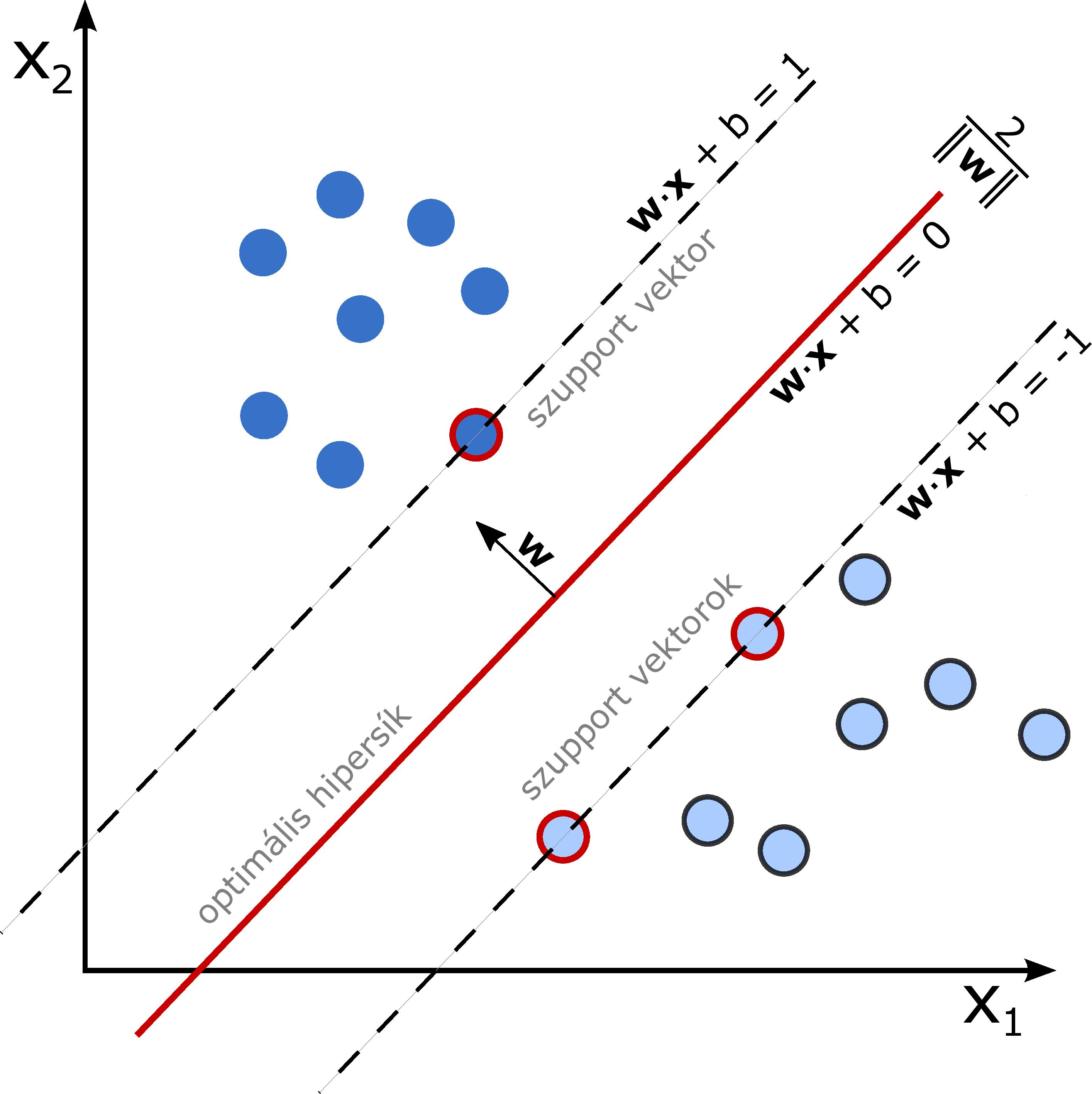
3. ábra. Optimális hipersík maximális margóval
Természetesen a gyakorlatban ritka az, hogy a mintában szereplő adatok lineárisan szeparálhatók. Ezt a problémát először úgy oldjuk fel, hogy ugyan továbbra is egy lineáris osztályozót konstruálunk, de segédváltozókat adva a korábbi optimalizálási probléma peremfeltételeihez megengedjük, hogy az osztályozó hibázzon a mintapontokban. A hibákat egy 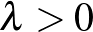 segédparaméterrel súlyozzuk a költségfüggvényben. A relaxált megoldást szolgáltató új feladat szintén konvex kvadratikus, így hatékonyan megoldható:
segédparaméterrel súlyozzuk a költségfüggvényben. A relaxált megoldást szolgáltató új feladat szintén konvex kvadratikus, így hatékonyan megoldható:
Ebben az esetben a 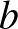 paraméter egy olyan
paraméter egy olyan 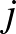 indexű peremfeltételből fejezhető ki, amelyre
indexű peremfeltételből fejezhető ki, amelyre 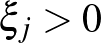 . Ezt a feladatot szokás gyenge margójú lineáris szupport vektor osztályozásnak nevezni. Vegyük észre, hogy a gyenge margójú esetben a margó értelmezése nem teljesen egyértelmű, a margót megsértő adatpontok miatt. A
. Ezt a feladatot szokás gyenge margójú lineáris szupport vektor osztályozásnak nevezni. Vegyük észre, hogy a gyenge margójú esetben a margó értelmezése nem teljesen egyértelmű, a margót megsértő adatpontok miatt. A 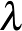 regularizációs paramétert a gyakorlatban általában keresztvalidáció segítségével hangolják be.
regularizációs paramétert a gyakorlatban általában keresztvalidáció segítségével hangolják be.
A segédváltozók bevezetése ugyan kiterjeszti a megoldást olyan esetekre is, amikor a két osztályból kapott minták szigorú értelemben nem választhatók ketté egy hipersíkkal – mert a két osztály mintái összekeveredtek – de (2) még mindig a lineáris osztályozók terében keres modellt. Tanulmányunk folytatásában megmutatjuk majd, hogy a nemlineáris problémák esetét hogyan lehet visszavezetni a lineáris osztályozók elméletére a kernel módszerek segítségével. Az alapötlet az lesz, hogy transzformáljuk az adatainkat egy nagy (akár végtelen) dimenziós térbe, amelyben már azok lineárisan szeparálhatóak.
Irodalomjegyzék
- [1] Boyd, S. P., and Vandenberghe, L. Convex Optimization. Cambridge University Press, 2004.
[2] Devroye, L., Györfi, L., and Lugosi, G. A Probabilistic Theory of Pattern Recognition, vol. 31. Springer Science & Business Media, 2013.
[3] Russel, S. J., and Norvig, P. Artificial Intelligence: A Modern Approach, 4th ed. Prentice Hall Series in Artificial Intelligence. Pearson, 2020.
[4] Samoili, S., Cobo, M. L., Gómez, E., De Prato, G., Martínez, Plumed, F., and Delipetrev, B. AI Watch: Defining artificial intelligence. Towards an operational definition and taxonomy of artificial intelligence. JRC Research Reports of the European Commission, JRC118163 (2020).
[5] Schölkopf, B., and Smola, A. J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press, 2002.
[6] Shawe-Taylor, J., Bartlett, P. L., Williamson, R. C., and Anthony, M. Structural risk minimization over data-dependent hierarchies. IEEE Transactions on Information Theory 44, 5 (1998), 1926–1940.
[7] Vapnik, V. Statistical Learning Theory. Wiley-Interscience, 1998.
Tamás Ambrus és Csáji Balázs Csanád
HUN-REN SZTAKI és ELTE Matematikai Intézet












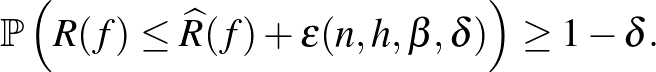
![$\displaystyle \mbox{\begin{tabular}{lll}
$\mathop{\hbox{minimalizáljuk}}\limit...
...n $k=1,\dots, n$\\ [3mm]
&$\xi_k \geq 0$&minden $k=1, \dots, n$
\end{tabular}}$](/images/stories/latexuj/2024-02/2024-02-statisztikustanulaselmelet1/img107.png)