Információk

Főmenü

 Aktuális szám: 31. szám 2024. március 

Möbius-síkok, blokkrendszerek, Møbee játék

Möbius-síkok, blokkrendszerek, Møbee játék

 

 

Tavaly év végén került piacra a Møbee nevű kártyajáték, aminek a szabálya nagyon egyszerű, egymondatos: Csapj fel három lapot a pakliból, és keresd meg azt az egyetlen figurát, amelyik mindhármon szerepel! A leggyorsabb játékos nyeri a kört. Ahhoz, hogy ilyen paklikat gyártsunk (a kiadott játék három különböző nehézségi szinthez tartozó paklit tartalmaz), érdekes kombinatorikai struktúrákra, az ún. 3-blokkrendszerekre van szükségünk.

1. definíció. Legyen 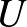$U$ nemüres, 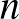$n$-elemű halmaz. Az 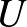$U$ feletti 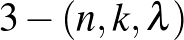$3-(n,k,\lambda)$ blokkrendszeren 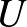$U$ olyan kitüntetett 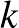$k$-elemű részhalmazainak (amelyeket blokkoknak nevezünk) halmazát értjük, amire teljesül, hogy 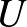$U$ bármely három különböző elemét választva mindig éppen 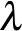$\lambda$ olyan blokk van, ami mindhármat tartalmazza.

Az első természetes kérdés, hogy mely paraméterek esetén léteznek ilyen 3-blokkrendszerek. A kérdésre a (részleges) választ, pontosabban három szükséges feltételt ad az alábbi tétel:

1. tétel. (Oszthatósági feltételek) Ha létezik 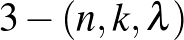$3-(n,k,\lambda)$ blokkrendszer, akkor teljesülnek az alábbi oszthatóságok.

1. 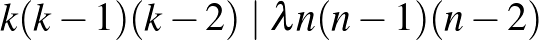  $k(k-1)(k-2) \mid \lambda n(n-1)(n-2)$,

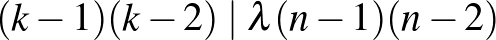2.  $(k-1)(k-2) \mid \lambda (n-1)(n-2)$,

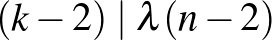3.   $(k-2) \mid \lambda (n-2)$.

A bizonyítás egyszerűen elvégezhető, elegendő rendre a blokkok számát, az egy rögzített 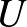$U$-beli elemet tartalmazó blokkokat, illetve egy rögzített 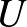$U$-beli elempárt tartalmazó blokkokat összeszámolni és felhasználni, hogy az eredményül kapott törtek mind egészek.

A továbbiakban feltételezzük, hogy 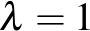$\lambda=1$. Az ilyen blokkrendszereket Steiner-rendszereknek szokták nevezni.

Kiindulva egy 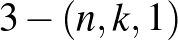$3-(n,k,1)$ Steiner-rendszerből, természetes módon tudunk gyártani olyan 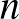$n$-lapos paklit, ahol minden lapon ugyanannyi figura szerepel és bármely három lapon pontosan egy azonos közöttük (de bármely kettő lapon több közös figura is szerepel, elkerülendő azt a „triviális” paklit, ahol van egy olyan figura, ami minden lapon szerepel). Legyenek a pakli lapjai az 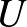$U$ elemei, a figurák pedig a blokkrendszer blokkjai. Egy figura pontosan akkor szerepeljen egy lapon, ha a neki megfelelő blokk tartalmazza a lapnak megfelelő 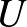$U$-beli elemet. Az így kapott pakli a definíció szerint rendelkezik azzal a tulajdonsággal, hogy bármely három lapján mindig pontosan egy figura közös, továbbá a lapok száma 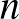$n$, a felhasznált figurák száma 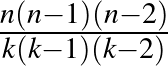$\frac{n(n-1)(n-2)}{k(k-1)(k-2)}$, az egy lapon szereplő figurák száma pedig 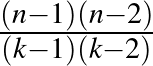$\frac{(n-1)(n-2)}{(k-1)(k-2)}$. Két lapon a közös figurák száma éppen 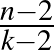$\frac{n-2}{k-2}$ és minden figura 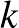$k$ lapon fordul elő. (Ezeket az értékeket kaptuk, amikor a fenti oszthatósági feltételeket bizonyítottuk.)

Az oszthatósági feltételeket végignézve 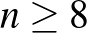$n \geq 8$ esetekre, a legkisebb nemtriviális (azaz 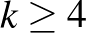$k \geq 4$) lehetőség megkonstruálása az alábbi feladat.

Házi feladat. Konstruáljunk 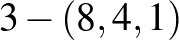$3-(8,4,1)$ blokkrendszert!

Segítség. Az alaphalmaz elemei legyenek egy kocka csúcsai, a blokkok pedig olyan 4 csúcsot tartalmazó részhalmazok, mint például a kocka oldallapjai, szimmetriasíkjai (ezek eddig mind olyan síkok, amik a kockának pontosan 4 csúcsára illeszkednek). Ezeken kívül még 2 olyan csúcsnégyes kell, ahol semelyik kettő csúcs közt nem halad él. Ezeknek a blokkoknak a száma a fentiek alapján éppen 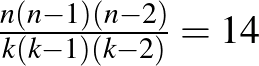$\frac{n(n-1)(n-2)}{k(k-1)(k-2)}=14$ és minden csúcsot 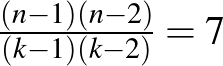$\frac{(n-1)(n-2)}{(k-1)(k-2)}=7$ blokk tartalmaz.

A feladatot megoldva megkonstruálhatjuk a Møbee játékban szereplő legkisebb, 8-lapos paklit.

A konstrukció könnyen általánosítható, egy 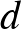$d$-dimenziós kocka csúcsaiból kiindulva, megfelelő 4-elemű blokkokat (csúcsnégyeseket) véve kapható 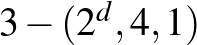$3-(2^d,4,1)$ paraméterű blokkrendszer. Ennek kidolgozását az olvasóra hagyjuk.

Az oszthatósági feltételeket teljesítő 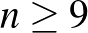$n \geq 9$, nemtriviális blokkrendszerekhez (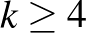$k \geq 4$) tartozó paraméterhármasok, ahol az egy rögzített elemet tartalmazó blokkok száma, azaz 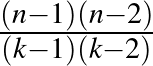$\frac{(n-1)(n-2)}{(k-1)(k-2)}$ legfeljebb 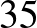$35$ (ez a konstruált pakliban az egy lapon szereplő figurák száma, így természetes, hogy érdemes korlátozni a játszhatóság érdekében):

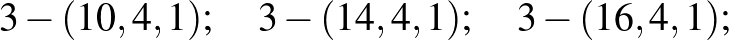
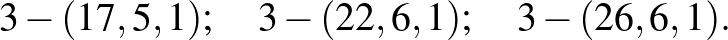
$\displaystyle 3-(10,4,1);\quad 3-(14,4,1);\quad 3-(16,4,1); $    $\displaystyle 3-(17,5,1);\quad 3-(22,6,1);\quad 3-(26,6,1). $

Ezek közül a harmadik az előbb említett módon egy 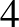$4$-dimenziós kocka csúcsaiból konstruálható meg. Az első, negyedik, és hatodik blokkrendszerek konstrukciója pedig elvezet a jelen cikk legfontosabb véges geometriai objektumainak, a Möbius-síkoknak a fogalmához.

A listán a második blokkrendszer konstrukciója nem véges geometriai jellegű, azt itt most nem tárgyaljuk. Az ötödik blokkrendszer (a 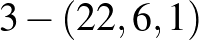$3-(22,6,1)$) pedig a 4-rendű projektív síkot (aminek 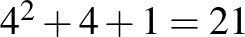$4^2+4+1=21$ pontja és ugyanennyi egyenese van) 1 ponttal bővítve konstruálható, ahol az új blokkok (összesen 77) a sík bizonyos oválisait (ezek itt olyan ponthalmazok amelyeknek semelyik 3 pontja nem kollineáris, összesen 56-ra lesz szükségünk belőlük) és az összes egyenesét (ez 21 darab egyenes) felhasználva adhatók meg.

Möbius-síkok

A klasszikus Möbius-sík egy illeszkedési struktúra, amelynek pontjai a háromdimenziós euklideszi térben egy rögzített gömb felszíni pontjai, körei pedig a gömbfelszín nemérintő síkmetszetei. Az illeszkedési reláció a természetes módon definiált illeszkedés. Erre a struktúrára nyilvánvalóan teljesül hogy bármely 3 különböző pontjára pontosan egy olyan kör van, ami mindháromra illeszkedik, mégpedig a három (nem-kollineáris) pont által meghatározott sík és a gömbfelszín metszete.

A klasszikus Möbius-sík véges analógiái a véges Möbius-síkok, amelyeket az alábbi három axiómával definiálunk:

2. definíció. Egy 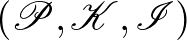$(\mathcal{P},\mathcal{K},\mathcal{I})$ hármas véges Möbius-sík, ahol 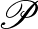$\mathcal{P}$ a pontok véges halmaza, a körök véges halmaza 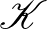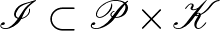$\mathcal{K}$, $\mathcal{I} \subset \mathcal{P} \times \mathcal{K}$ pedig az illeszkedési reláció, ha:

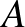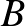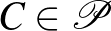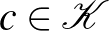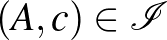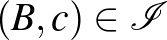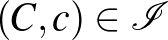1. minden $A$, $B$, $C\in \mathcal{P} $ páronként különböző pontra létezik pontosan egy olyan $c \in \mathcal{K}$ kör, amire $(A,c) \in \mathcal{I}$, $(B,c) \in \mathcal{I}$, $(C,c) \in \mathcal{I}$,

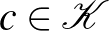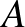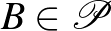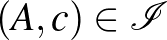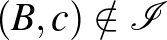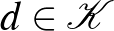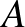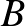2. minden $c \in \mathcal{K}$ körre és $A$, $B\in \mathcal{P}$ pontokra, ahol $(A,c) \in \mathcal{I}$, de $(B,c)\notin \mathcal{I}$, létezik pontosan egy olyan $d \in \mathcal{K}$, amely illeszkedik $A$ és $B$ pontokra is és 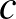$c$ körrel csak 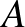$A$ a közös pontja,

3. van 4 olyan pont, amely nem egy körre illeszkedik.

Könnyen látható, hogy a klasszikus Möbius-sík a végességi feltételeken kívül mindent teljesít ezek közül.

Tekintsünk egy véges Möbius-síkot és rögzítsük egy 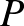$P$ pontját. Ha a ponthalmazból elhagyjuk ezt a rögzített pontot, és egyeneseknek hívjuk a 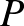$P$-re illeszkedő köröket (persze 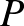$P$ nélkül), belátható, hogy az így adódó illeszkedési struktúra egy véges affin sík (gondoljuk meg, hogy ugyanez történik a klasszikus Möbius-síkon amikor a gömbfelszín egy kijelölt pontjából sztereografikus projekciót hajtunk végre), aminek ismertek a kombinatorikus tulajdonságai (pontok száma, egyenesek száma, egy egyenesre illeszkedő pontok száma stb.). Így a kiindulási Möbius-sík rendelkezik az ezekből következő kombinatorikus tulajdonságokkal, amelyeket az alábbi tétel foglal össze.

2. tétel. Legyen 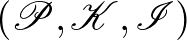$(\mathcal{P},\mathcal{K},\mathcal{I})$ véges Möbius-sík, ahol egy 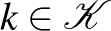$k \in \mathcal{K} $ kör pontosan 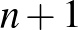$n+1$ pontra illeszkedik. Ekkor teljesülnek a következők.

1. Minden 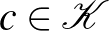$c \in \mathcal{K}$ körre pontosan 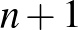$n+1$ pont illeszkedik.

2. A pontok száma 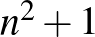$n^2+1$, a körök száma pedig $n(n^2+1)$.

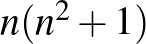3. Minden pontra 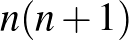$n(n+1)$ kör illeszkedik.

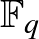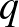A következőkben megmutatjuk, hogy hogyan lehet véges Möbius-síkokat konstruálni. Ehhez először egy véges testtel koordinátázott háromdimenziós projektív térre lesz szükségünk, ahol a pontok homogén koordinátákkal írhatók le. Jelölje $\mathbb{F}_q$ a $q$ elemű testet, ahol 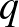$q$ prímhatvány.

Definiáljunk az 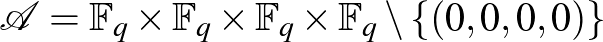$\mathcal{A}=\mathbb{F}_q\times\mathbb{F}_q\times\mathbb{F}_q\times\mathbb{F}_q\setminus \{(0,0,0,0)\} $ halmazon egy relációt a következőképpen:

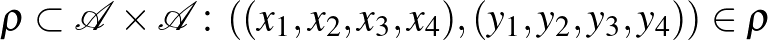
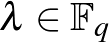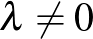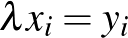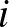$\rho\subset\mathcal{A}\times \mathcal{A}\colon ((x_1,x_2,x_3,x_4),(y_1,y_2,y_3,y_4)) \in \rho$ $\iff$ létezik $\lambda\in \mathbb{F}_q$, $\lambda \ne 0$, amire $\lambda x_i=y_i $, minden $i$-re.

Megmutatható, hogy a 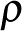$\rho$ reláció ekvivalencia-reláció.

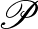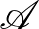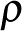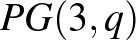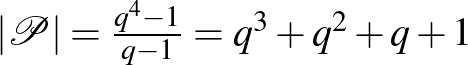Legyen a $\mathcal{P}$ ponthalmazunk az $\mathcal{A}$ halmazon $\rho$ relációhoz tartozó osztályok halmaza. Bevezetve az egyenesek és a síkok fogalmát ezen a ponthalmazon, kapjuk a $PG(3,q)$-val jelölt háromdimenziós projektív teret. Egyszerűen adódik, hogy a tér pontjainak száma: $\vert\mathcal{P}\vert=\frac{q^4-1}{q-1}=q^3+q^2+q+1$.

A klasszikus Möbius-sík definíciójánál felhasznált gömb analógiájaként most 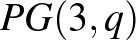$PG(3,q)$-ban tekintsünk egy nemelfajuló másodrendű felületet, egy elliptikus kvádrikát, amit (legalábbis páratlan 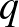$q$ esetén) az 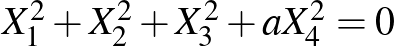$X_1^2+X_2^2+X_3^2+aX_4^2=0$ egyenlet ír le egy megfelelően választott 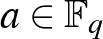$a \in \mathbb{F}_q$ elemre (páros, azaz kettőhatvány 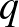$q$-ra ez az egyenlet kicsit bonyolultabban adható meg). 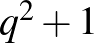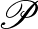Megmutatható, hogy pontosan $q^2+1$ olyan $\mathcal{P}$-beli pont (osztály) van, amire ez teljesül. Ez a 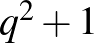$q^2+1$ elemű ponthalmaz lesz a Möbius-síkunk ponthalmaza. Az is könnyen látszik, hogy ebben a ponthalmazban semelyik három pont nem kollineáris (mellesleg ezzel a tulajdonsággal, a lehető legnagyobb méretű ponthalmaz a térben, ún. ovoid). Megmutatható továbbá, hogy a 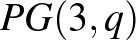$PG(3,q)$ tér minden síkja vagy érinti vagy pontosan 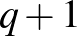$q+1$ pontban metszi az ovoidot. A Möbius-sík körei legyenek ezen utóbbi, 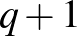$q+1$ pontot tartalmazó részhalmazok, az illeszkedés pedig legyen a tartalmazás. A véges Möbius-sík axiómái teljesülnek az így definiált struktúrára, ellenőrzésük nem túl bonyolult számolási feladat. Az így kapott, 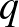$q$-elemű testre épített véges Möbius-síkok valóban 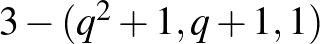$3-(q^2+1,q+1,1)$ blokkrendszereknek is tekinthetők, melyekből 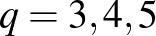$q=3,4,5$ esetekben rendre 10, 17 és 26 lapos Møbee paklikat tudunk gyártani, 12, 20 és 30 figurával egy-egy lapon.

Természetesen a probléma (és a játék) tovább általánosítható például a 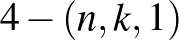$4-(n,k,1)$ blokkrendszerek fogalmának bevezetésével, amikből olyan kártyajátékok készíthetők, ahol bármely 4 lapon van mindig pontosan 1 közös figura (míg 4-nél kevesebb lapon mindig egynél több közös figura van). Egy ilyen nemtriviális (azaz 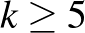$k \geq 5$) 4-blokkrendszer, a 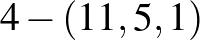$4-(11,5,1)$ blokkrendszer, aminek konstrukciója az egyik (a legkisebb elemszámú, szokásosan 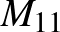$M_{11}$-gyel jelölt) Mathieu-csoportot használja. A származtatott pakli minden lapján 30 figura szerepel, és már kevesen tudják élvezettel játszani. Ha továbbmegyünk, és nemtriviális 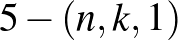$5-(n,k,1)$ blokkrendszereket szeretnénk konstruálni, majd a megfelelő játékot legyártani, ezt is megtehetjük, de nem kapunk olyan paklit, ami a „játszható” tartományba esne. Ha esetleg még nehezíteni szeretnénk és nemtriviális 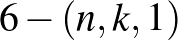$6-(n,k,1)$ blokkrendszereket gyártanánk (ahol 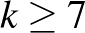$k \geq 7$), sajnos azzal a problémával szembesülünk, hogy ezidáig nem találtak ilyet (Peter Keevash egy eredménye szerint biztosan léteznek ilyenek, bár nyilván a játszhatósági tartományon jócskán kívül eső paklikat eredményeznek).

A másik továbblépési lehetőség a 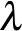$\lambda$ értékének 2-re változtatásával, 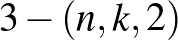$3-(n,k,2)$ blokkrendszerekből olyan paklikat gyárthatunk, amelyeknél bármely három lapon mindig pontosan két közös figura szerepel. Ezek gyors megtalálása a játékosok feladata.

A játékban benne van az edukációs felhasználás lehetősége is, például ha a figurákat helyettesíthetjük festményekkel, irodalmi művekekkel, városokkal, akkor három lapot felcsapva kereshetjük azt a festőt, írót, országot akinek/aminek mindhárom lapon van műve, városa. Elképzelhető, hogy ilyen gamifikációs megoldásokkal a közoktatásban is hasznosítható lesz a Møbee, illetve annak verziói.

 A cikk megjelenését támogatta az NKFI az SNN 132625 számú OTKA pályázat keretében.

Irodalomjegyzék

[1] Hajnal Péter: Halmazrendszerek – Polygon jegyzettár 2002.
[2] Kárteszi Ferenc: Bevezetés a véges geometriákba, Akadémiai kiadó, 1973.
[3] Kiss György, Szőnyi Tamás: Véges geometriák, Polygon, 2001.
[4] Keevash, P.: The existence of designs, https://doi.org/10.48550/arXiv.1802.05900.
 
Ruff János
PTE TTK Matematikai és Informatikai Intézet

 

 

A Pécsi Tudományegyetem Természettudományi Kar Matematikai és Informatikai Intézet adjunktusa, Ruff János és csapata készítette el a MØBEE kártyajátékot, ami hasonlít arra a népszerű (Dobble) kártyajátékra, amelyben az egyforma ábrákat kell megkeresni a lapokon, de annál komplexebb, más játékélményt nyújt. Honlapja a  https://mobeecards.store. A játékot bemutató youtube-videó itt található.