Hatszögletű inspiráció

Mindig is szakácsként szerettem volna dolgozni, és a konyha – bármilyen konyha – számomra az a hely, ahol a kreativitásom felragyog, ahol természetes módon jutok el a flow állapotába, ezért gyakran szoktam mondani, hogy a múzeumpedagógia nagyon hasonlít a főzéshez. Mindkettőhöz hozzátartozik az összetevők megfelelő aránya, a tetszetős tálalás és kivitelezés. A múzeumpedagógusok többnyire besétálnak a már berendezett kiállításokra, elolvassák, amit a kurátorok a képekről kiírtak, és értelmezik az egészet. A múzeumpedagógusoknak általában nincs beleszólásuk abba, hogy mi hova kerüljön, és a tárgyak hogyan legyenek bemutatva. Múzeumpedagógusként nekem az a szerepem, hogy hidat építsek a látogatók és a kiállított tárgyak között. Mi a siker receptje? Megfelelő összetevők a megfelelő mennyiségben, a megfelelő pillanatban. Milyen összetevők? Eddigi tapasztalataim alapján a kontextus megadása, a művek csendes szemlélése, a gondolatok megosztása egymással, a háttérinformáció megértése és közös kreatív játék kézzel fogható eszközkészletekkel az az öt megközelítés, amelyet minden csoportnál alkalmazok, függetlenül a látogatók korától vagy attól, hogy milyen minőségükben látogatnak ide. Írásom egy konkrét kézzel fogható készletet mutat be – a Hexamandala kirakót.

1. ábra. Hexamandala

A Hexamandala Gondos Gábor kirakójátékai iránti szenvedélyemből született. Miután először meglátogattam Gábor honlapját, tudtam, hogy ezeket a puzzle-okat be szeretném építeni a múzeumpedagógiai munkámba. Nemcsak gyönyörűek voltak, de közelebbről megvizsgálva őket, rájöttem, hogy bennük rejlik a lehetőség, hogy a látogatók jobban megértsék Victor Vasarely (1906–1997) néhány műalkotásának szerkezetét, valamint a műalkotások alapjául szolgáló matematikai és művészeti fogalmakat.

Miután összeraktam néhány kirakójátékát, azonnal megvettem a Napszirom és a Juhar kirakóit (2.ábra). A legegyszerűbben úgy lehet őket összerakni, ha a középpontos szimmetriát használjuk, és az azonos méretű darabokat körkörösen ugyanabba a pozícióba helyezzük a keret szélén. Gábor elmagyarázta, mi a siker titka: a nagyobb darabokkal kell kezdeni. Hamar rájöttem, hogy a nagyobb darabok a kisebbekből állnak össze (3. ábra). A kirakóinak ez a felépítése lehetővé teszi, hogy sokféleképpen össze lehessen rakni őket. Mi döntjük el, hogy milyen lesz a végleges kompozíció.


2. ábra. Napszirom	Juhar	3. ábra. Napszirom (részletek)

Victor Vasarely, a magyar-francia művész, aki az op-art művészeti irányzat egyik kimagasló képviselője volt, hasonló módon használta a síkidomokat. A Napszirom puzzle-hoz hasonlóan Vasarely is sok hatszögletű kompozíciót töltött meg más síkidomokkal. Néha rombuszokat használt, különbözőképpen elrendezve őket (https://vasarely.hu/mutargyak/15530/, https://vasarely.hu/mutargyak/15550/).

A Trybox című festmény esetében három nagyobb rombuszon belül köröket, ellipsziseket és oválisokat (íves formákat) rendezett el.

Vasarely Múzeum Budapest

Amikor a budapesti Vasarely Múzeum gyűjteményének egy műalkotásával párba állítható kirakót kerestem, félretettem a Napszirom puzzle-t, mert vékony darabjai nem bírták volna a múzeumi foglalkozásokkal járó igénybevételt. Amikor Gábor meglátta a Trybox című festmény ellipszisekből és körökből álló belső szerkezetét, a Körmandala kirakót javasolta, és kölcsön is adta (4. ábra). Egyébként ez volt Gábor első kirakójátéka. Az ösztöneim azonban azt súgták, hogy a Körmandala túl nagy, és túl sok darabból áll a múzeumlátogatás során rendelkezésre álló időhöz és helyhez képest. Megkérdeztem, hogy nem lehetne-e egy kisebb változatot készíteni belőle. Gábor azonnal igent mondott. Közösen döntöttük el, hogy milyen alakzatokat fogunk használni. Mivel a Körmandala kirakó és a Trybox című festmény belső szerkezete is hatszög, megegyeztünk abban, hogy az új kirakó kerete is hatszög (hexagon) lesz, és így Gábor Hexamandalának nevezte el. Mivel a múzeumban a kirakóst és a keretet is stancgéppel szerettem volna kivágni, úgy döntöttünk, hogy a keret is darabok közé kerül (5. ábra).


4. ábra. Körmandala	5.ábra. Hexamandala (részlet)

A Hexamandala egyik legfontosabb jellemzője, hogy a tükrözést és a forgatást, azaz a tengelyes és a középpontos szimmetriát is használhatjuk az összerakásához (6. és 7. ábra). Először gyerekeket, tizenéveseket és felnőtteket kértem meg, hogy rakják össze a kirakót tengelyes szimmetria szerint. Mivel láttam, hogy nehezen boldogulnak, megkértem a tesztelőket, hogy az elemek elforgatásával, azaz a középpontos szimmetria szabályai szerint rakják össze. Percek alatt elkészültek.


6. ábra. Hexamandala (részlet)	7. ábra. Hexamandala (részlet)

Nem sokkal később a kezembe került Miranda Lundy Sacred Geometry című könyve. Alig hittem a szememnek, amikor megláttam a 7. oldalon lévő ábrát (8. ábra). A körök által kimetszett alakzatok pontosan úgy néztek ki, mint a Hexamandala darabjai. Gábor megerősítette a felvetésemet. Amikor annakidején a Körmandala kirakót megtervezte, körzővel rajzolta meg az alakzatokat. A könyvben látott alakzatok arra inspiráltak, hogy a Hexamandalát és a Tryboxot új módon használjam fel. Miután kivettem a kirakó elemei közül a keretet és a legnagyobb elemet (9. ábra), megkértem a látogatókat, hogy nézzék meg, hány kört tudnak létrehozni a megmaradt darabokból. (10. ábra).

8. ábra

9. ábra. Hexamandala (részlet)

10. ábra. Hexamandala (részlet)

Vasarely gyakran töltött ki formákat körökkel és ellipszisekkel, mert ezekkel mozgást ábrázolhatott. Ahhoz, hogy lássuk, mi volt a szándéka, vágjunk ki egy kört kartonból. Álljunk egy fal mellé, amelyet erős fény világít meg. Fogjuk meg a kört a legszélén, mozgassuk a fény előtt, és nézzük meg, hogyan változik az árnyék alakja ellipszissé. Azzal, hogy keskenyebb és szélesebb ellipsziseket ábrázolt, és más, íves síkidomokká torzította őket, Vasarely a tér, a mozgás és az idő fogalmát építette be a kompozícióba. A három szabályos rombusz közepén lévő alakzatok felnagyításával a távolságot – a nézőtől való távolságot – is ábrázolta, mivel az emberi látórendszer a nagyobb tárgyakat közelebbinek, a kisebbeket pedig távolabbinak érzékeli.

A fenti leírás összefoglalja a Hexamandala kirakóval és a Trybox című festménnyel végzett eddigi munkámat. Mit hoz a jövő? Remélem, hogy a Hexamandalához, a Tryboxhoz és a hatszögekhez kapcsolódó következő matematikai fogalmakat is bemutathatom a budapesti Vasarely Múzeum látogatóinak.

Az alábbi témák felhasználhatók a kirakóban, a festményben és általában a hatszögekben rejlő egyes matematikai fogalmak bemutatására, megértésük elmélyítésére vagy felmérésére.

Minden hatszögnek hat oldala van. A hat a legkisebb tökéletes szám, mivel önmagánál kisebb pozitív osztóinak összege (1+2+3=6). A Hexamandala kirakóban minden színes darabból hat példány van. A kirakós összesen tizenháromféle darabból áll. A tizenhárom prímszám, akárcsak a három, a rombuszok száma, amelyekre Vasarely a Trybox című festményt felosztotta. Hány darab van összesen? Az iskolások gyakorolhatják a szorzást és az összeadást (vagy kivonást), hogy megtalálják a 13 × 6 összeszorzásának leggyorsabb módját. Vajon kiszámolják, mennyi 10 x 6 és 3 × 6, majd összeadják?? Azok, akik a műveleti sorrendet tanulják, hogyan írnák fel a matematikai gondolatmenetüket visszaadó képletet? Használhatjuk szöveges feladatként is: ha összesen tizenháromféle elem van, és minden elemből hat-hat példány, hány darabból áll a kirakós?

Az összeadást gyakorló tanulók felsorolhatják az összes lehetőséget, hogy 1-től 13-ig pozitív egész számok felhasználásával 2, 3, 4,…tagból álló összegként állítsák elő a 13-atas összeget: 1+12, 1+1+11, 1+2+3+7. A negatív egész számok gyakorlására olyan feladatokat is fel lehet adni, amelyekben az összeg negatív számokat is tartalmaz.

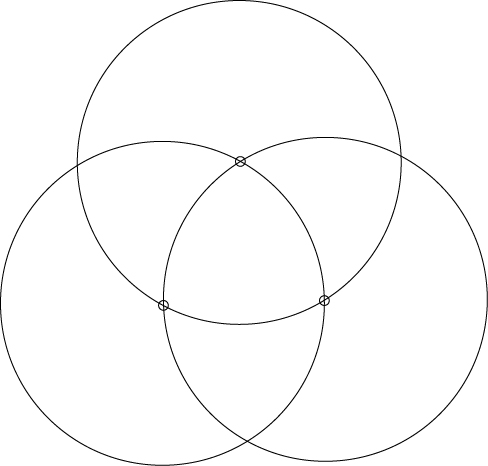
Visszatérve a pozitív osztókra, a diákok megkereshetik a 78-as szám összes osztóját. Hasonlóképpen, mivel a Trybox című festményben minden egyes rombusz 15 × 15 íves alakzatból álló rácsot tartalmaz, a tanulók a 225 osztóit is megkereshetik, vagy megtehetik ugyanezt akár a két vagy mindhárom rombuszban lévő íves alakzatok teljes számával, a 450-nel, illetve a 675-tel. Hasonlóképpen a négyzetgyökök és hatványok témáját is be lehet vezetni, hiszen 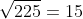, illetve .

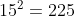Ha csoportban oldják meg a feladványt, az is lehet, hogy a puzzle darabokat egyenlően osztják el a csoport tagjai között. Nehezíti a feladatot, hogy a 13 prímszám. Megkérdezhetjük, hogyan osztanák el egyenlően a darabokat 2 vagy 3 tagú csoportokban, és milyen javaslatot tennének a 4 fős csoportokra.

Ha megkérdezzük a tanulókat, hogy melyik darabbal kezdték és hogyan folytatták a kirakóst, kérhetjük, hogy római számokkal írják le a sorrendet. Bár a Hexamandala kirakó sokféleképpen összerakható, néha üres helyekre és oda nem illő darabokra bukkanunk (11. ábra). A kirakós befejezéséhez néhány darabot ki kell venni a már kirakottak közül, és másikkal helyettesíteni. Ezekben az esetekben, amikor leírják, hogyan sikerült befejezniük, a olyan szavakat használhatnak a sorrend leírására, mint az utolsó vagy utolsó előtti.

11. ábra. Hexamandala (részlet)

Fent említettem, hogy Gábor kirakóinak nagyobb darabjai a kisebbekből állnak össze. Ezért a Hexamandala darabjaival az egybevágóság, és ezen belül a nagyobb mint, a kisebb mint és az egyenlő fogalmát is vizsgálhatjuk. A tanulók továbbá a darabok (12.ábra) elrendezésével és kombinálásával gyakorolhatják az egybevágóság megértését, és felfedezhetik a törtek és a terület témakörét. Ha ezekben a témákban már járatosak, akkor használhatják a kirakót a százalékokról tizedes számokra való átváltás gyakorlására is. Utolsó kihívásként megkérdezhetjük tőlük, hogy a kereten belüli terület teljesen lefedhető-e csak egyfajta elemmel, és ha igen, van-e többféle elem, amely erre alkalmas?

12. ábra. Hexamandala (részlet)

A Trybox című festményben Vasarely ugyanannyi zöld, piros és narancsbarna színt használt. A Hexamandala nálunk meglévő hat példánya más-más mennyiségben tartalmazza a kék három és a zöld két árnyalatát. A tanulók kiszámolhatják, hogy az egyes színek milyen arányban vannak jelen az egyes kirakókban.

A Trybox példaként használható a szabályos hatszögek és rombuszok meghatározó tulajdonságainak, köztük az élek számának megértéséhez, valamint a belső és külső szögek méréséhez.

Bár minden hatszögnek több szimmetriatengelye van, a puzzledaraboknak már nem feltétlenül. A diákokat meg lehet kérni, hogy a Hexamandala darabjait két csoportra osszák: azokra, amelyeknek van legalább egy szimmetriatengelye, és azokra, amelyeknek nincs. A diákokat arra is meg lehet kérni, hogy kreatívan használják fel a kirakó darabjait, és alkossanak olyan kompozíciót, amely legalább egy szimmetriatengellyel rendelkezik. (13. ábra).

13. ábra. Hexamandala (részlet)

A geometriai transzformációk témáját a Trybox című festmény megtekintésekor lehet megbeszélni, mivel minden rombusz és minden rombuszban található íves alakzat kétszeres eltolással keletkezik a másikból. Ezt a témát a tanulók jobban megérthetik úgy, ha a Hexamandala kirakót rakják össze. Azokat a tanulókat, akik jártasak a grafikai tervezőprogramok használatában, megkérhetjük, hogy állapítsák meg, vajon a Trybox nagyobb íves síkidomai nagyításai-e valamelyik kisebbnek.

Ahogy írtam: a kirakós darabjai közül kettő kivételével mindegyikből össze tudunk állítani köröket. A tanulókat megkérdezhetjük, hogy melyik darabot használnák a körök sugarának mérésére, és a darab melyik részét mérnék. Az összes lehetséges darab megmérésével meglátják, hogy az egyiket könnyebb-e megmérni, mint a másikat, és hogy ugyanazt a hosszúságot kapják-e. A budapesti Vasarely Múzeumban kézzel, stancoló géppel elkészítendő kirakó tervezésekor némileg módosítani kellett a darabok méretét. Emiatt nem illeszkednek olyan szorosan egymás mellé, mint ahogyan lehetne. Bár ez a kérdés inkább a mérnöki munkával és az alapanyagok természetével kapcsolatos, nem a matematikával, jelentős szerepet játszott a kirakó elkészítésében. Ha a tanulók ismerik az összerakott kör (hozzávetőleges) sugarát, akkor ki tudják számítani a kör hozzávetőleges kerületét és hozzávetőleges területét, valamint az egyes darabok területét és néhány darabon lévő ív hosszát (14. ábra).

14. ábra. Hexamandala (részlet)

Azáltal, hogy a tanulók a különböző feladatok során újra és újra visszatérnek a kirakókészlethez, kézzel fogható eszközökkel tanulnak. Mind Gábor, mind én azt reméljük, hogy ez megerősíti a különböző matematikai fogalmak megértését és azokkal kapcsolatos ismereteiket, és lehetővé teszi, hogy ezeket más helyzetekben is alkalmazzák, például amikor műalkotásokat vitatnak meg, és saját innovatív kompozícióikat tervezik.

Juhász Litza múzeumpedagógus

Vasarely Múzeum Budapest