Az elmélet haszna – avagy inkább végy föl két zoknit...

Gian-Carlo Rota (1932–1999, https://mathshistory.st-andrews.ac.uk/Biographies/Rota/) – aki többek között a számos kiadásban megjelent differenciálegyenletekről szóló [1] tankönyv társszerzője – időnként szerette írásban megfogalmazni az oktatásra vonatkozó véleményét mások (és saját (!)) okulására.

Differenciálegyenletek

A differenciálegyenletek tanítására vonatkozó állításai közül a legtöbbel nehéz egyet nem érteni; klaviatúrát nyilván azért ragadtam, mert van viszont olyan kijelentése, amelyiket vitatni szándékozom. Azt javasolja, [5] hogy ne foglalkozzunk túl sokat a megoldások létezésére és egyértelműségére vonatkozó alapvető tételekkel. Ezeknek az állításoknak azonban (akár gyakorlati szempontból is) fontosnak nevezhető következményei is vannak, amint az alábbi példákból ki fog derülni. Részletesebben: idézünk két, jól ismert elméleti eredményt (1. tétel és 2. tétel), majd példákon mutatjuk meg gyakorlati fontosságukat. Nem térünk ki itt arra, hogy a differenciálegyenletek (elméleti és alkalmazási szempontból egyaránt fontos) kvalitatív elméletének kiinduló pontjai az egzisztencia- és unicitási tételek, ld. pl. [6].

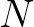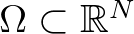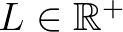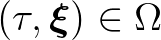Induljunk ki a következőkből. Legyen $N$ pozitív egész szám, $\Omega\subset \mathbb{R}^N$ tartomány, $\mathbf{f}\colon \Omega\longrightarrow\mathbb{R}^N$ olyan függvény, amelyiknek a deriváltja normában korlátos és nem nagyobb, mint az $L\in\mathbb{R}^+$ szám, továbbá legyen $(\tau,\boldsymbol{\xi})\in\Omega$ .

1. tétel. (Picard–Lindelöf) Az

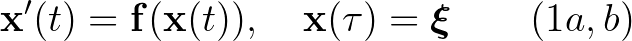
$\displaystyle \mathbf{x}'(t)=\mathbf{f}(\mathbf{x}(t)),\quad \mathbf{x}(\tau)=\boldsymbol{\xi}\quad\quad(1a,b)$

kezdetiérték-problémának létezik megoldása valamilyen pozitív 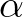$\alpha$ szám mellett a $]\tau-\alpha,\tau+\alpha[$ intervallumon, és ez a megoldás egyértelmű.

1. példa. Az $N=1$ esetben a tételben szereplő kezdetiérték-problémának nem létezik nemtriviális periodikus megoldása.

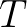Bizonyítás. Tegyük fel, hogy a $\boldsymbol{\varphi}$ folytonosan differenciálható függvény a fenti kezdetiérték-probléma periodikus megoldása, akkor létezik olyan pozitív $T$ szám, hogy minden 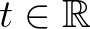$t\in\mathbb{R}$ esetén 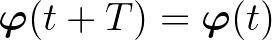$\boldsymbol{\varphi}(t+T)=\boldsymbol{\varphi}(t)$ . Legyen 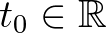$t_0\in\mathbb{R}$ olyan pont, ahol a 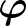$\boldsymbol{\varphi}$ függvénynek szélső értéke van, akkor 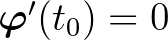$\boldsymbol{\varphi}'(t_0)=0$ . Tekintsük ezek után a fenti differenciálegyenlet 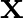$\mathbf{x}$ megoldását az 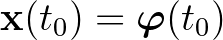$\mathbf{x}(t_0)=\boldsymbol{\varphi}(t_0)$ kezdeti feltétel mellett. 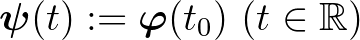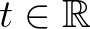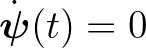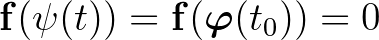Ennek a kezdetiérték-problémának nyilván megoldása a $\boldsymbol{\psi}(t):=\boldsymbol{\varphi}(t_0){\ }(t\in\mathbb{R})$ képlettel értelmezett (állandó) függvény, hiszen minden $t\in\mathbb{R}$ estén $\dot{\boldsymbol{\psi}}(t)=0$ , és $\mathbf{f}(\psi(t))=\mathbf{f}(\boldsymbol{\varphi}(t_0))=0$ . Másrészt a 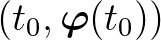$(t_0,\boldsymbol{\varphi}(t_0))$ ponton pontosan egy megoldás halad át, ezért 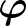$\boldsymbol{\varphi}$ nem lehet más, mint a fent bevezetett 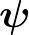$\boldsymbol{\psi}$ állandó megoldás.

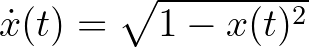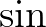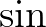Fölvetődhet, hogy de hiszen az $\dot{x}(t)=\sqrt{1-x(t)^2}$ egyenletnek megoldása a periodikus szinuszfüggvény. Ez azonban nem igaz, mert ennek az egyenletnek a megoldásai csak olyan függvények lehetnek, amelyeknek a deriváltja kizárólag nemnegatív értéket vesz fel. Ilyen a $\sin$ függvény valamely leszűkítése, például a $\sin_{\vert]\frac{3\pi}{2},\frac{5\pi}{2}[}$ függvény. (A $\sin$ függvényt azért szorítottuk meg egy nyílt intervallumra, mert differenciálegyenlet megoldásának első közelítésben nyílt intervallumon értelmezett függvényeket szokás nevezni.)

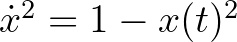Mi a helyzet az $\vert\dot{x}\vert=\sqrt{1-x(t)^2}$ és az $\dot{x}^2={1-x(t)^2}$ egyenletekkel? Ezekre a Picard–Lindelöf-tétel nem vonatkozik, ugyanis ezek nem explicit differenciálegyenletek.

2. példa. Az $\dot{x}=x-xy, \dot{y}=xy-y$ Lotka–Volterra-egyenletről könnyen belátható, hogy vannak periodikus megoldásai, ugyanis a

$\displaystyle H(\overline{x},\overline{y}):=\overline{x}+\overline{y}-\ln(\over... ...line{y}) \quad ((\overline{x},\overline{y})\in\mathbb{R}^+\times\mathbb{R}^+)$

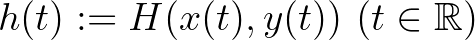összefüggéssel értelmezett $H$ függvény ennek első integrálja, azaz a $h(t):=H(x(t),y(t)){\ }(t\in\mathbb{R})$ képlettel értelmezett függvény a megoldások mentén állandó, hiszen $\dot{h}(t)=0$ . Akkor viszont – mivel a megoldások trajektóriái a $H$ függvény szintvonalain haladnak, és ezek a szintvonalak zárt görbék – a megoldások periodikus függvények.

Ezek után felvethető a következő kérdés: előfordulhat-e, hogy a megoldások koordinátafüggvényei ugyanabban a $t$ pontban veszik fel szélsőértéküket? A korábbi érvelést alkalmazva látható, hogy a Picard–Lindelöf-tétel szerint ez lehetetlen.

1. ábra. A Lotka–Volterra-egyenlet egy megoldása, a hozzá tartozó trajektória és a megoldás koordinátafüggvényei

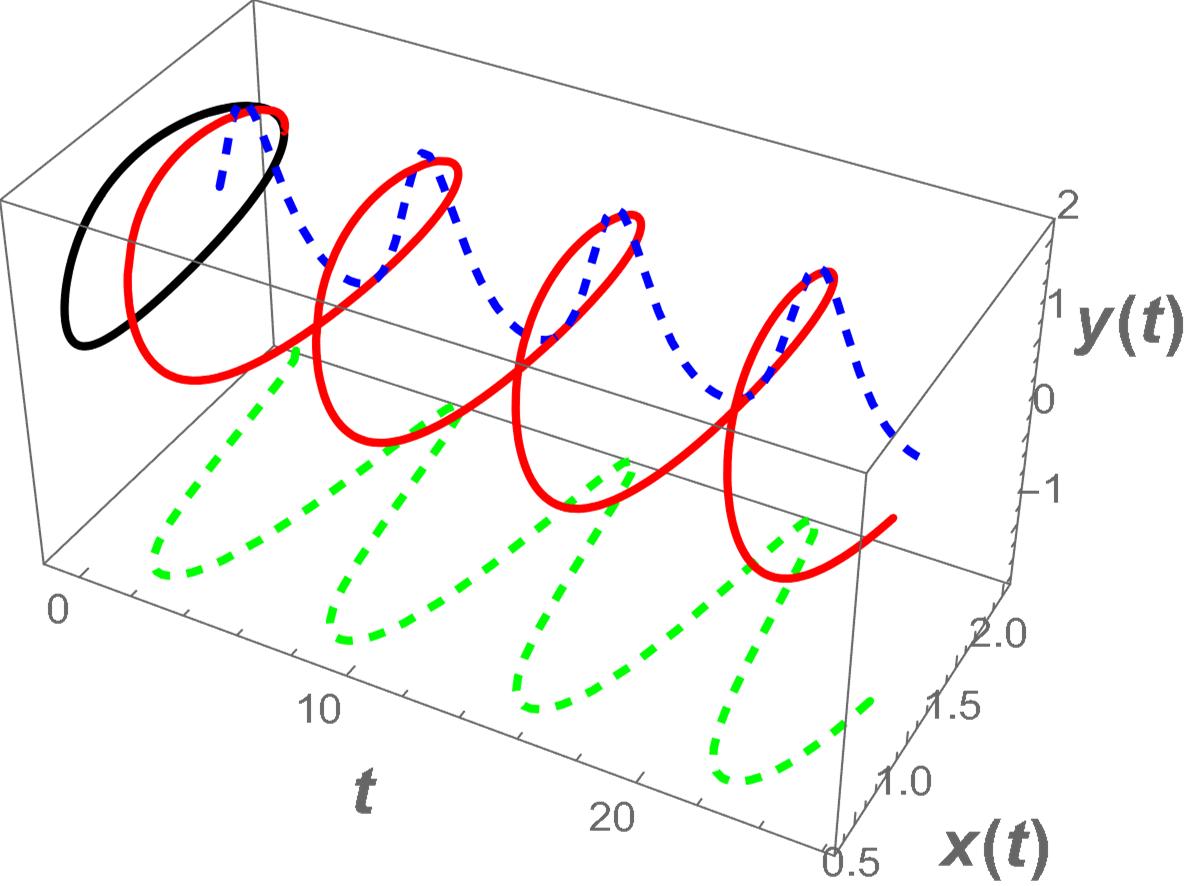
Általában is igaz az az állítás, hogy az (1a) differenciálegyenletnek nincsen olyan (nemtriviáis) periodikus megoldása, amelynek összes koordinátafüggvénye ugyanott vesz fel szélsőértéket. Póriasan: a csúcsok és völgyek szükségképpen eltolódnak egymáshoz képest. Hasonlóan ahhoz, ahogyan a költő [2, 623. oldal] mondja:

                               „Nem stoppolok, inkább
végy föl két zoknit, hisz nincsenek egy helyen úgysem
mind a lukak.”

2. ábra. A Lotka–Volterra-egyenlet első integrálja és az általa definiált felületen fekvő egyik zárt trajektória

Még egy, elméleti szempontból alapvető állításról mutatjuk meg, hogy az (akár matematikán kívüli) alkalmazásokhoz is sok köze van.

2. tétel. (Peano-egyenlőtlenség) Tekintsük az

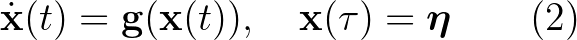
$\displaystyle \dot{\mathbf{x}}(t)=\mathbf{g}(\mathbf{x}(t)),\quad \mathbf{x}(\tau)=\boldsymbol{\eta}\quad\quad(2)$

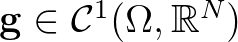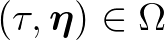kezdetiérték-problémát is, ahol $\mathbf{g}\in\mathcal{C}^1(\Omega, \mathbb{R}^N)$ és $(\tau,\boldsymbol{\eta})\in\Omega$ . Legyen valamilyen pozitív $\delta$ számmal

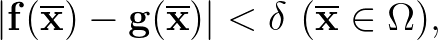
$\displaystyle \vert\mathbf{f}(\overline{\mathbf{x}})-\mathbf{g}(\overline{\mathbf{x}})\vert<\delta{\ }(\overline{\mathbf{x}}\in\Omega),$

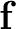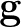és tegyük fel, hogy $\mathbf{f}$ és $\mathbf{g}$ egyaránt olyan függvény, amelyiknek a deriváltja normában korlátos és nem nagyobb, mint az 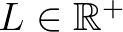$L\in\mathbb{R}^+$ szám. Ha 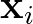$\mathbf{x}_i$ az (i) kezdetérték-feladat megoldása (i=1,2), akkor eltérésük a következőképp becsülhető:

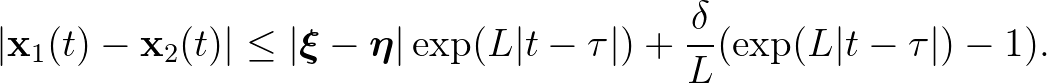
$\displaystyle \vert\mathbf{x}_1(t)-\mathbf{x}_2(t)\vert\le \vert\boldsymbol{\xi... ...ert\exp({L\vert t-\tau\vert})+\frac{\delta}{L}(\exp({L\vert t-\tau\vert})-1).$

Világos, hogy a becslés első tagja a kezdeti állapot mérésének hibájától függ, és ennek csökkentésével tetszőlegesen kicsivé tehető. A második tag pedig (amennyiben $\mathbf{f}$ írja le helyesen a jelenséget és ennek $\mathbf{g}$ a modellje) a modell hibájától függ, a modell javításával ez a tag is tetszőlegesn kicsivé tehető. Mindenesetre az egyenlőtlenség megmutatja, hogy a kísérletezőnek és a modellezőnek egymásra mutogatás helyett érdemesebb összefognia...

Az eltérés tehát minden véges intervallumon tetszőlegesen kicsinnyé tehető, ami nem zárja ki a nagy eltéréseket végtelen hosszú intervallumon, hiszen a becslés mindkét tagjában exponenciális függvény szerepel, vagyis a Peano-egyenlőtlenség nem mond ellent annak, hogy szép egyenletek megoldásai is nagyon érzékenyek lehetnek a kis eltérésekre.

3. példa. Számítsuk ki (numerikusan) a Lorenz-egyenlet

$\displaystyle \dot{x}=-3 (x - y), \quad \dot{y}= -x z + 26.5 x - y, \quad \dot{z}= x y - z,$

két megoldása különbségének normáját, és becsüljük meg ezt az eltérést a Peano-egyenlőtlenség felhasználásával is.

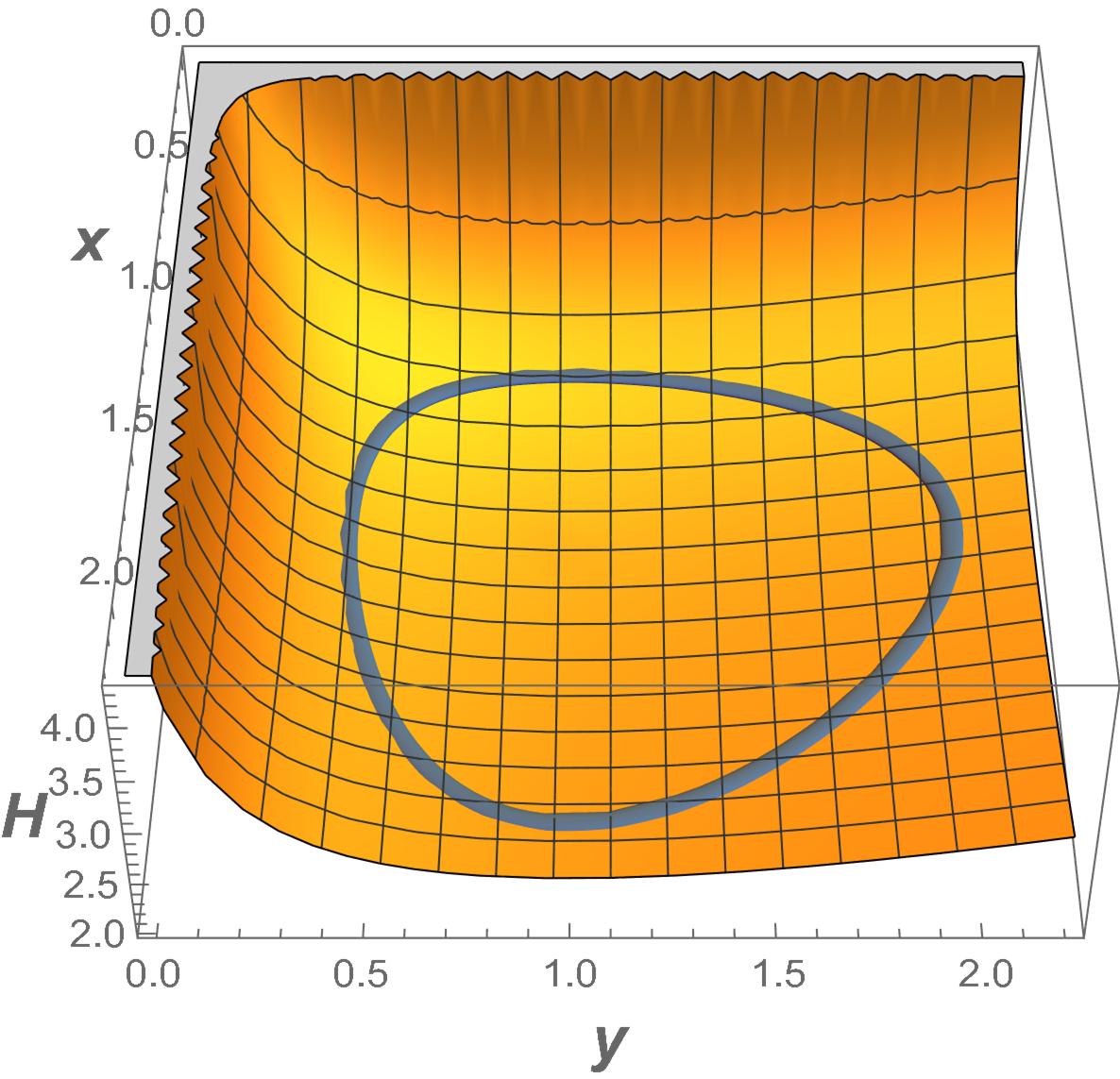
Szükségünk lesz a jobb oldal deriváltja normájának becslésére. Ehhez keresünk egy korlátos zárt halmazt, amelyben a trajektóriák benne maradnak. Ez a halmaz egy alkalmasan választott ellipszoid, lásd a 3. ábrát.

3. ábra. A Lorenz-egyenlte trajektóriái és egy bennfoglaló ellipszoid

Ezek után kiszámoljuk a devivált mátrix normáját ezen az ellipszoidon, ami becsülhető a 6 számmal.

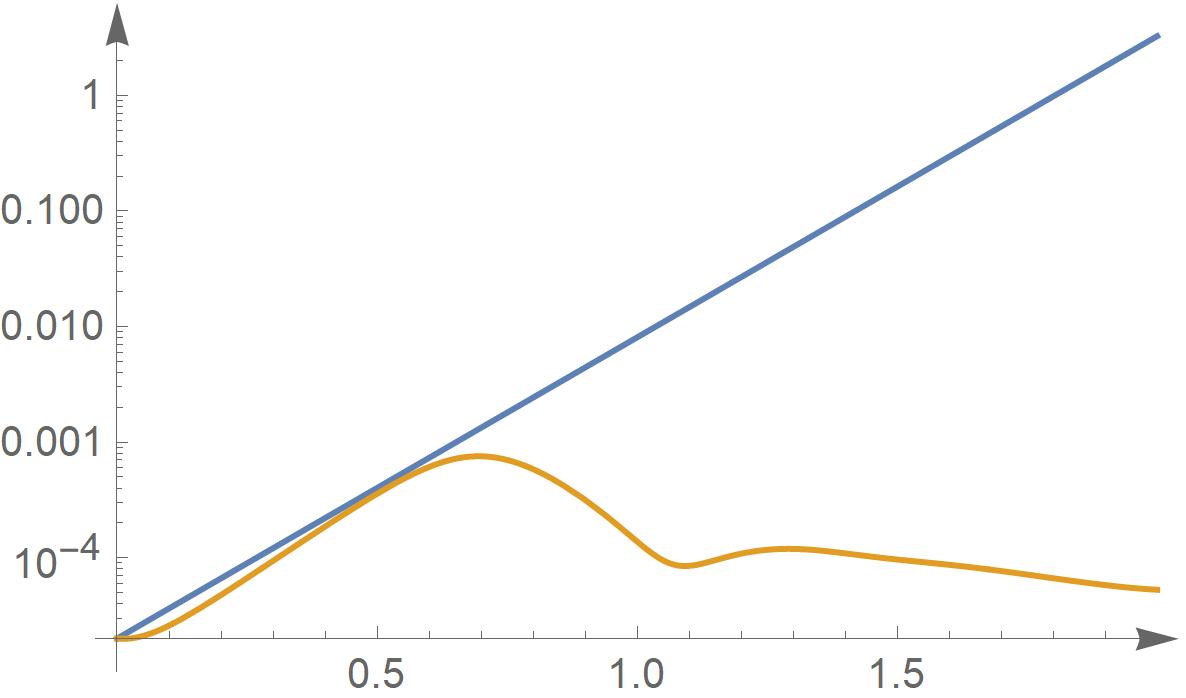
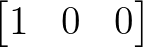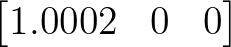4. ábra. A Lorenz egyenlet $\begin{bmatrix}1&0&0\end{bmatrix}$ és $\begin{bmatrix}1.0002&0&0\end{bmatrix}$ kezdeti állapotból indított megoldása különbségének normája és a Peano-egyenlótlenségből adódó becslés.

Ha csak a kezdeti értékek különböznek, akkor a Peano-egyenlőtlenségnek csak első tagja különbözik nullától.

Publikáció

Másik, nem kevésbé tanulságos intelemsorozata [4] , amelynek fordítását az Érintő is közölte, szintén nem maradt kritikai visszhang nélkül. Névai Pál [3] – nem kevés tisztelettel adózva a szerzőnek – kiemelt három tanácsot, amelyekkel szemben komoly ellenérveket sorakoztatott fel, ennek a vitának az áttekintését házi feladatul adjuk az olvasónak. Ha eközben eljut az https://people.math.osu.edu/nevai.1/QUIZ/quiz.txt oldalra, további örömökben is része leend.

Irodalomjegyzék

[1] Birkhoff, Garrett and Rota, Gian-Carlo: Ordinary differential equations. Introductions to Higher Mathematics. Ginn and Company, Boston, Mass., 1962.

[2] Devecseri Gábor: Utószó, In: Quintus Horatius Flaccus összes versei, Corvina Kiadó, Budapest, 1961.

[3] Névai Pál: Ten lessons I wish I had never been taught by Gian-Carlo Rota. Notices of the AMS 44 (3) (1997), 309–310.

[4] Rota, Gian-Carlo: Ten lessons I wish I had been taught. Notices of the AMS 44 (1) (1997), 22–25.

[5] Rota, Gian-Carlo: Ten lessons I wish I had learned before I started teaching differential equations. In: Palombi F. (eds) Indiscrete Thoughts. Modern Birkhäuser Classics. Birkhäuser, Boston, MA. 1997.

[6] Simon L. Péter: Differenciálegyenletek és dinamikai rendszerek, Eötvös Loránd Tudományegyetem, Matematikai Intézet, Alkalmazott Analízis és Számításmatematikai Tanszék, Budapest, 2012. https://simonp.web.elte.hu/files/dinrendjegyzet.pdf

[7] Tóth János és Simon L. Péter: Differenciálegyenletek. Bevezetés az elméletbe és az alkalmazásokba. (3. kiadás) Typotex, Budapest, 2020.

Tóth János