Mi is... egy nyitott könyv?

A nagyon kifejező nyitott könyv fogalmat H. E. Winkelnkemper vezette be 1973-ban megjelent [3] dolgozatában, és egy olyan geometriai struktúrát értett alatta, mely akkor már meglehetősen hosszú idő óta ismert volt. Egy 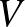$V$ sima (valós) sokaságon értelmezett nyitott könyv (vagy nyitottkönyv felbontás) egy 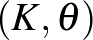$(K, \theta)$ párból áll, melyek a következőket teljesítik:

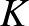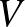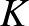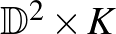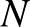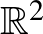a sokaság két kodimenziós valódi részsokasága, melynek normálnyalábja triviális – így -nak van egy ${\mathbb{D}}^2\times K$ -val diffeomorf környezete (ahol ${\mathbb{D}}^2$ az ${\mathbb{R}}^2$ zárt egységgömbjét jelöli), melyben 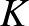maga mint 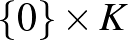$\{ 0\}\times K$ helyezkedik el;
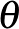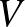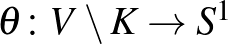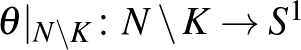$\theta$ pedig egy lokálisa triviális (sima esetén tehát egy kritikus pont nélküli) sima $\theta \colon V\setminus K\to S^1$ fibrálás, melyre teljesül, hogy létezik -nak egy olyan környezete, amire $\theta$ -t megszorítva a normális anguláris koordinátát kapjuk, vagyis $\theta \vert _{N\setminus K}\colon N\setminus K\to S^1$ a kézenfekvő

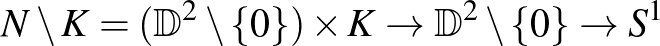
$\displaystyle N\setminus K=({\mathbb{D}}^2\setminus \{ 0\})\times K\to {\mathbb{D}}^2\setminus \{ 0\} \to S^1$

projekciók kompozíciója.

A 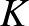$K$ részsokaságot a nyitott könyv kötésének (mivel a gerinc már más topológiai fogalmat jelöl), míg 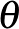$\theta$ fibrumait, pontosabban azok lezártjait, a nyitott könyv lapjainak nevezzük.

A fogalom alapvető példáját adja az 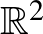${\mathbb{R}}^2$ -en értelmezett nyitott könyv, melynek kötése az origó, a lapok pedig az origóból kiinduló 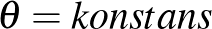$\theta =konstans$ félegyenesek, ahol 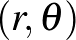$(r, \theta)$ a szokásos polárkoordinátákat jelöli. Ezt valamely 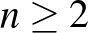$n\geq 2$ esetén 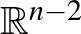${\mathbb{R}}^{n-2}$ -vel megszorozva 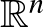${\mathbb{R}}^n$ -en kapjuk a standard nyitott könyvet, mely a kötés körüli lokális képet mutatja, és 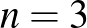$n=3$ -ra valóban úgy néz ki, mint egy 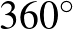$360^{\circ}$ -ban kinyitott könyv. Az USA-ban régebben előszeretettel használt, telefonszámok feljegyzésére szolgáló Rolodex nevű forgó kartotékozó épp így néz ki.

Nyitott könyvek más nevek alatt is felbukkannak az irodalomban – mint globális Poincaré–Birkhoff-szelések, relatív leképezés-tóruszok, Lefschetz- vagy Milnor-fibrálások, fibrált láncok, pörgethető struktúrák –, mutatva azt a változatosságot, amely kontextusokban ez a fogalom természetesen felmerül – ilyenek a dinamikai rendszerek, komplex algebrai geometria, algebrai vagy geometriai topológia.

Poincaré „utolsó geometriai tétele” szerint a körgyűrű olyan területtartó leképezésének, amely a két határkört ellentétes irányba forgatja, legalább két fixpontja van. E tétel valójában a háromtest-problémára ad egy periodikus megoldást. Poincaré munkájában a körgyűrű (az annulus) úgy jelenik meg, mint a generált vektormező globális szelése egy 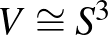$V\cong S^3$ energiaszinten, vagyis egy olyan 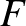$F$ kompakt felületként, mely minden orbitot metsz, peremét érinti a vektormező, de belseje transzverz a vektormezőre. Következésképp a vektormező 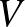$V$ -n megfigyelhető dinamikáját az 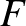$F$ annuluson jelentkező „első visszatérési leképezés” teljesen meghatározza. Továbbá, 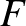$F$ -et a vektormező mentén mozgatva 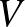$V$ -t végigsúroljuk annulusok egy 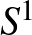$S^1$ családjával, melyek határa ugyanaz: ezek az annulusok egy nyitott könyvet alkotnak 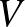$V$ -n.

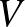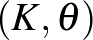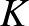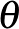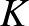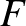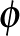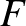Egy tetszőleges $V$ sokaságon lévő tetszőleges $(K, \theta)$ nyitott könyv leírható így, mivel léteznek olyan integrálható vektormezők, melyek érintik $K$ -t és transzverzálisak $\theta$ fibrumaira. Olyan vektormezőket tekintve, melyek eltűnnek $K$ mentén, a nyitott könyvek következő általános konstrukcióját kapjuk. Legyen $F$ egy peremes sokaság és $\phi$ az $F$ -nek egy olyan önmagára vonatkozó diffeomorfizmusa, mely a peremen az identitás. A 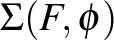$\Sigma (F, \phi)$ leképezés-tórusz, vagyis az 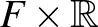$F\times {\mathbb{R}}$ szorzatnak a 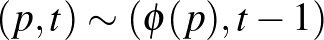$(p,t)\sim (\phi (p), t-1)$ ekvivalenciarelációval vett hányadosa egy 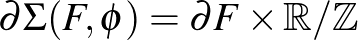$\partial \Sigma (F, \phi)=\partial F\times {\mathbb{R}}/{\mathbb{Z}}$ peremű sokaság. Minden 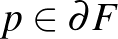$p\in \partial F$ esetén a 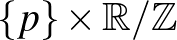$\{ p\}\times {\mathbb{R}}/{\mathbb{Z}}$ köröket pontra ejtve egy perem nélküli 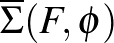${\overline {\Sigma }}(F,\phi)$ sokaságot kapunk, melyet a 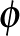$\phi$ relatív leképezés-tóruszának szokás nevezni. Ez a sokaság egy természetes nyitott könyvet hordoz, melynek kötése 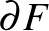$\partial F$ egy kópiája – melyet $\partial F \times {\mathbb{R}}/{\mathbb{Z}}$ -ből kapunk a faktorizálás során – és amelynek leképezését a körvonalra az 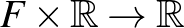$F\times {\mathbb{R}}\to {\mathbb{R}}$ projekcióból nyerjük, így a nyitott könyv lapjai 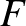$F$ kópiái lesznek. A 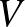$V$ sokaságon értelmezett 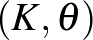$(K, \theta)$ nyitott könyv monodrómiájának nevezzük az 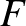$F$ lap minden olyan önmagára vonatkozó 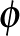$\phi$ diffeomorfizmusát, amelyre létezik egy olyan 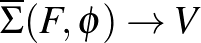${\overline {\Sigma}} (F, \phi)\to V$ diffeomorfizmus, mely a 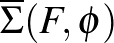${\overline {\Sigma }}(F,\phi)$ -n lévő kézenfekvő nyitott könyvet 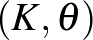$(K, \theta)$ -ba viszi.

Egy háromdimenziós sokaságban lévő egyszerű zárt görbét csomónak, míg csomók véges és diszjunkt unióját láncnak nevezünk. A lánc akkor fibrált, ha előáll, mint egy nyitott könyv kötése. Elágazó fedések és láncok fonataira vonatkozó munkáinak következményeként 1920 körül J. Alexander belátta, hogy minden zárt 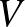$V$ három-sokaságban létezik fibrált lánc. Valóban, az 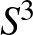$S^3$ gömbfelületen van egy triviális 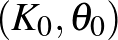$(K_0, \theta _0)$ nyitott könyv (az 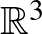${\mathbb{R}}^3$ -on értelmezett standard nyitott könyv egypontú kompaktifikációja), és 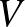$V$ előállítható 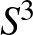$S^3$ egy olyan fedéseként, mely egy lánc mentén elágazik. Ez a lánc pedig előáll fonatként, vagyis egy izotópia segítségével a 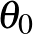$\theta _0$ fibrumaira transzverzzé tehető, így 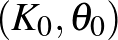$(K_0, \theta _0)$ visszahúzása 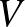$V$ -n egy nyitott könyvet ad.

Nevezetes példák adódnak magasabb dimenziós nyitott könyvekre azokon a páratlan dimenziójú gömbökön, melyek holomorf függvények izolált szingularitásaihoz tartoznak. Ha az 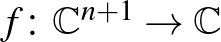$f\colon {\mathbb{C}}^{n+1}\to {\mathbb{C}}$ komplex polinomnak az origó izolált kritikus pontja és 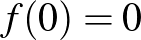$f(0)=0$ , Milnor fibrálási tétele szerint elég kis 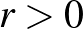$r>0$ esetén az alább definiált 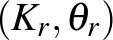$(K_r, \theta _r)$ pár egy, az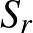 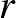$S_r$ $r$ -sugarú, origó középpontú gömbfelületen ad nyitott könyv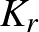et:

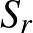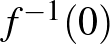-et és az $f^{-1}(0)$ hiperfelület transzverz metszete adja, míg
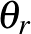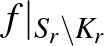$\theta _r$ az $f\vert _{S_r\setminus K_r}$ függvény szöge.

Milnor-fibrálásokat a múltban is intenzíven vizsgáltak, és V. I. Arnold vette észre – majd S. K. Donaldson és P. Seidel eredményei megerősítették –, hogy ezek a fibrálások szorosan kapcsolódnak szimplektikus geometriához: a fibrum egy természetes szimplektikus formát – vagyis egy nemelfajuló zárt 2-formát – hordoz, melyet a monodrómia megőriz, és melyre a Picard−Lefschetz-féle eltűnési ciklusok Lagrange-féle – vagyis féldimenziós izotróp – gömbök.

Azok a feltételek, melyek teljesülése esetén egy adott sokaságon létezik nyitott könyv, I. Tamura, H. Winkelnkemper, T. Lawson és F. Quinn munkásságának köszönhetően jól ismertek és meglehetősen enyhék (lásd a [2] cikket a pontos állításokért). Például minden páratlan dimenziós sokaságon van nyitott könyv. Másrészt viszont nyitott könyvek számos topológiai probléma megoldásában bizonyultak hasznos eszköznek, mint például diffeomorfizmusok bordizmus-csoportjainak kiszámolásában, vagy (a W. Thurston által adott végleges megoldás megtalálása előtt) 1-kodimenziós fóliázások találásában. W. Thurston és H. Winkelnkemper arra is használták a nyitott könyveket, hogy (újra) belássák, minden irányított három-sokaságon található kontakt struktúra. Valójában a legújabb eredmények (lásd az [1] cikket további információkért) azt mutatják, hogy „szimplektikus nyitott könyvek” (amelyek nyitott könyvek egy meglehetősen széles osztályát alkotják, és tartalmazzák az eddig bemutatott összes példát) szoros kapcsolatban állnak a kontakt geometriával, amely területen a nyitott könyvek különböző – topologikus, dinamikai, komplex analitikus – tulajdonságai természetes módon egyesülnek.

Irodalomjegyzék

[1] Emmanuel Giroux, Géométrie de contact: de la dimension trois vers les dimensions supérieures, Proc. Int. Cong. Math. (Bejing 2002, Vol II, 405–414, Higher Education Press, 2002.

[2] Frank Quinn, Open book decompositions, and the bordism of automorphisms, Topology 18 (1979), 55–73.

[3] Horst Elmar Winkelnkemper, Manifolds as open books, Bull. Amer. Math. Soc. 79 (1973), 45–51.

Emmanuel Giroux a Centre National de la Recherche Scientifique (CNRS) kutatási igazgatója, és az Unité de Mathématiques Pures et Appliquées de l'École Normale Supérieure de Lyon intézetben dolgozik. A fenti cikk 2005 januárjában jelent meg a Notices of the American Mathematical Society folyóiratban. Ez a fordítás a szerző engedélyével jelenik meg.

Fordította Stipsicz András.

Emmanuel Giroux, WHAT IS…an Open Book? Notices Amer. Math. Soc. 52 (January 2005) 42–43. © Emmanuel Giroux. https://www.ams.org/journals/notices/200501/what-is.pdf?trk=200501what-is&cat=collection