Bevezetés
Ebben a cikkben egy érdekes sejtést fogunk bemutatni, ami a matematika számos területéről tartalmaz elemeket. A sejtés szerteágazó, ezt jól mutatja, hogy gráftulajdonságok vizsgálata során fogalmazták meg, Boole-függvényeket használ, és a Fourier-analízis eszközeivel vizsgálják. Ezek mind a matematika egy-egy igen széles területét képezik, azonban a sejtés megértéséhez nem kell szakértőnek lenni egyik területen sem.
A számítógép-tudomány megjelenésével a matematikában előtérbe került az irányzat számára fontos területek vizsgálata. Ide tartoznak a bitsorozatokon értelmezett 0-1 értékű függvények (Boole-függvények) is, amelyek például áramkörök tervezésénél játszanak fontos szerepet. Az elméleti matematika segítségével, esetünkben a Fourier-analízis eszközeit használva, igen általános kontextusban is vizsgálhatóak ezek a függvények. Az így elért eredményeket aztán eredményesen tudják alkalmazni a kutatók és a fejlesztők a gyakorlati projektek megvalósításában.
Az entrópia-hatásfüggvény-sejtés ennek a területnek egy máig bizonyítatlan elméleti állítása. A jelentősége többek között abban is rejlik, hogy alsó becslést ad a címben szereplő hatásfüggvénynek nevezett mennyiségre. Ez ugyanis szorosan kapcsolódik az ún. küszöbjelenséghez (threshold phenomena, [4]): Tegyük fel, hogy egy rendszer rendelkezik egy valós paraméterrel és valamilyen esemény valószínűsége ezen paraméter változtatásától monoton módon függ. Gyakran a paraméterskála azon része az érdekes, ahol ez a valószínűség gyorsan változik a paraméter apró módosításától is. Ezeket az intervallumokat hívjuk küszöbintervallumnak. Ilyesfajta vizsgálódások nemcsak a fent említett számítógép-tudomány területén érdekesek, hanem alkalmazzák gazdasági folyamatok elemzésében és a politikatudományban is (lásd: [6]).
Az alábbiakban bemutatunk néhány fogalmat és állítást, amelyek segítségével aztán formába önthetjük az 1995-ben Ehud Friedgut és Gil Kalai által megfogalmazott sejtést. További érdekességként bemutatunk egy eredményt a kérdéskörben arról, hogy véletlen függvényekre a sejtés állítása „nagy valószínűséggel” teljesül.
Jelölések, alapfogalmak
Előzetesen néhány szó a jelölésekről, szóhasználatról. Az alábbiakban Boole-függvényekkel fogunk dolgozni. Ezek az irodalomban több különböző formában szerepelnek, előfordulnak 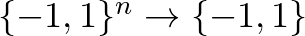 ,
,  ,
, 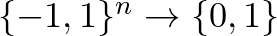 és
és 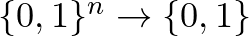 alakban is. Mi a második alakkal foglalkozunk, így ha Boole-függvényről beszélünk, akkor a képhalmaz mindig a
alakban is. Mi a második alakkal foglalkozunk, így ha Boole-függvényről beszélünk, akkor a képhalmaz mindig a 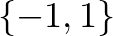 halmaz lesz, az alaphalmaz pedig
halmaz lesz, az alaphalmaz pedig  .
.
Néhány jelölés: Az 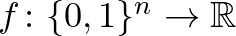 várható értékén az
várható értékén az 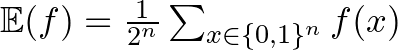 , míg az
, míg az 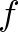 és
és 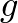 függvények skaláris szorzatán az
függvények skaláris szorzatán az 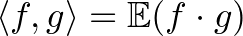 mennyiséget értjük. Egy
mennyiséget értjük. Egy 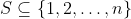 halmaz karakterisztikus vektora az az
halmaz karakterisztikus vektora az az 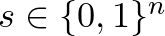 vektor, amelynek az
vektor, amelynek az 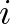 -edik koordinátája akkor és csak akkor
-edik koordinátája akkor és csak akkor 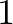 , ha
, ha  , egyébként 0.
, egyébként 0.
A cikkben igyekszünk csak a sejtés megfogalmazásához szükséges definíciók és állítások kimondására szorítkozni. Néhány állítás bizonyítása azonban kellően rövid és megértésükkel jobb betekintés nyerhető a terület gondolatvilágára. Ezeket a bizonyításokat a cikk végén gyűjtöttük össze.
Ahogy már a bevezetőben is említettük, a sejtéshez vezető úton a Fourier-analízis eszközeit fogjuk használni. Ehhez először definiáljuk a területen nagyon fontos szerepet játszó ún. karaktereket a mi speciális alaphalmazunk esetén:
1. definíció. Legyen 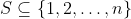 és
és 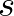 legyen ennek a halmaznak a karakterisztikus vektora. Ekkor az
legyen ennek a halmaznak a karakterisztikus vektora. Ekkor az 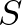 -hez tartozó karakter az a
-hez tartozó karakter az a 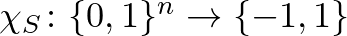 függvény lesz, amelyre:
függvény lesz, amelyre:
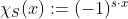 .
.
A kitevőben 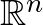 -beli vektorok szokásos skaláris szorzását használjuk.
-beli vektorok szokásos skaláris szorzását használjuk.
A továbbiakban az alsó indexekben egyaránt használjuk a halmazos és a karakterisztikus vektoros jelölést is, amikor egy halmazhoz tartozó karakterről beszélünk.
Mielőtt rátérnénk a Boole-függvényekre, először általánosabb, valós számokba képező függvényeket fogunk tekinteni. Belátható, hogy a 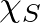 karakterek, ahol
karakterek, ahol 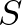 befutja az
befutja az 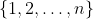 halmazt, ortonormált bázisát adják az
halmazt, ortonormált bázisát adják az 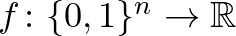 függvények alkotta vektortérnek. Azaz minden
függvények alkotta vektortérnek. Azaz minden 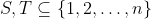 halmaz esetén
halmaz esetén 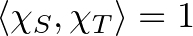 , ha
, ha  , és 0 különben, valamint minden
, és 0 különben, valamint minden 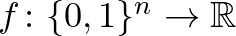 függvény felírható az alábbi módon:
függvény felírható az alábbi módon:
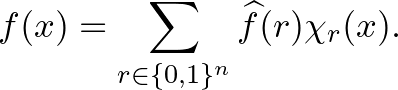
Az 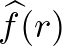 értékeket az
értékeket az 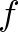 függvény
függvény 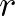 -hez tartozó Fourier-együtthatóinak nevezik. Az
-hez tartozó Fourier-együtthatóinak nevezik. Az 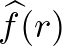 értékek seregét (ahogy
értékek seregét (ahogy 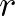 végigfut
végigfut  elemein) értelmezhetjük úgy, mint egy
elemein) értelmezhetjük úgy, mint egy 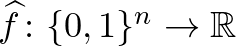 függvényt. Ezt a függvényt az
függvényt. Ezt a függvényt az 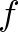 Fourier-transzformáltjának nevezik. Hasonlóan a karakterekhez,
Fourier-transzformáltjának nevezik. Hasonlóan a karakterekhez, 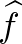 argumentumába időnként nem a karakterisztikus vektort, hanem a hozzá tartozó halmazt írjuk:
argumentumába időnként nem a karakterisztikus vektort, hanem a hozzá tartozó halmazt írjuk: 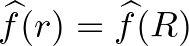 , ha
, ha 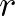 az
az 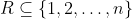 halmaz karakterisztikus vektora.
halmaz karakterisztikus vektora.
A következő néhány összefüggés rámutat a Fourier-együtthatók és az 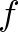 függvény kapcsolatára. Az olvasó mind a négy állítást könnyen ellenőrizheti a definíciók alapján.
függvény kapcsolatára. Az olvasó mind a négy állítást könnyen ellenőrizheti a definíciók alapján.
1. állítás. Igazak a következő egyenlőségek:
(i) 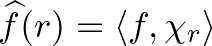 ;
;
(ii) 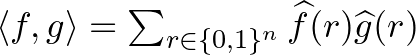 (Plancherel-tétel)
(Plancherel-tétel)
(iii) 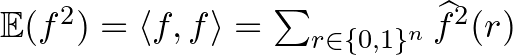 (Parseval-egyenlőség)
(Parseval-egyenlőség)
(iv) Boole-függvényekre  .
.
Hatásfüggvény, entrópia
Térjünk rá most kifejezetten a Boole-függvényekre, azon belül is a hatásfüggvény definíciójára. Legyen tehát adva egy 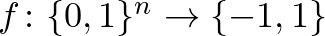 leképezés. Kérdés: mennyire függ a függvény értéke az
leképezés. Kérdés: mennyire függ a függvény értéke az 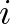 -edik argumentumtól? Azaz, ha megváltoztatjuk az argumentum
-edik argumentumtól? Azaz, ha megváltoztatjuk az argumentum 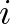 -edik koordinátáját, változik-e a függvény értéke?
-edik koordinátáját, változik-e a függvény értéke? 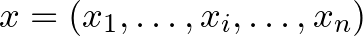 esetén jelölje
esetén jelölje 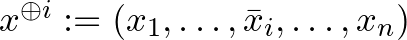 ezt a változást, ahol a felülvonás jelenti azt, hogy az
ezt a változást, ahol a felülvonás jelenti azt, hogy az 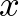
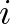 -edik koordinátáját az ellenkezőjére változtatjuk.
-edik koordinátáját az ellenkezőjére változtatjuk.
2. definíció. Az 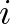 -edik változó hatásfüggvényének az
-edik változó hatásfüggvényének az
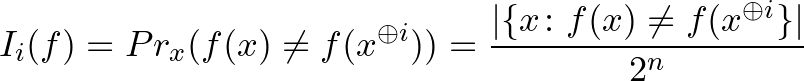
valószínűséget, míg 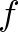 teljes hatásfüggvényének az
teljes hatásfüggvényének az
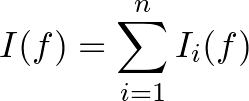
értéket nevezzük.
E definíció egy ügyes átfogalmazásával és némi számolással meg lehet mutatni, hogy az így definiált hatásfüggvény felírható pusztán a Fourier-együtthatók segítségével:
2. állítás.
![$\displaystyle I_i(f)=\sum_{S \subseteq [n], i\in S}\vert\widehat{f}(S)\vert^2.
$](/images/stories/latexuj/2021-08/2021-08-bakospalfy/img45.png)
Ebből az összefüggésből, az összegzések némi átrendezésével, a teljes hatásfüggvényre nézve a következő adódik:
3. állítás.
![$\displaystyle I(f)=\sum_{S \subseteq [n]}\vert S\vert\vert\widehat{f}(S)\vert^2.
$](/images/stories/latexuj/2021-08/2021-08-bakospalfy/img46.png)
Most térjünk át a címben is megjelenő másik fogalom, a Shannon-entrópia tárgyalására. Ez a fogalom számos más kontextusban is felbukkan a matematikában, de mindenhol hasonló jelentéssel (és definícióval) rendelkezik. A mi Boole-függvényekkel kapcsolatos vizsgálódásainkban a következőképpen vezethető be:
3. definíció. Legyen 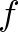 Boole-függvény. Az
Boole-függvény. Az 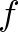 függvény (Shannon-féle) entrópiáján a
függvény (Shannon-féle) entrópiáján a
![$\displaystyle \mathbb{H}(f):=\sum_{S \subseteq [n], \widehat{f}(S)\neq 0 } {\widehat{f}}^2(S)\log\frac{1}{\widehat{f}^2(S)}
$](/images/stories/latexuj/2021-08/2021-08-bakospalfy/img47.png)
kifejezést értjük.
Mivel Boole-függvényeknél létezik nullától különböző Fourier-együttható, így ez az összeg nem lesz üres. Könnyen látható, hogy nemnegatív értékeket vesz fel, valamint a Jensen-egyenlőtlenség alkalmazásával (a 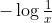 függvény konvexitását felhasználva) igazolható, hogy nem nagyobb mint
függvény konvexitását felhasználva) igazolható, hogy nem nagyobb mint 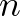 .
.
Az entrópia és a hatásfüggvény is valamilyen formában azt fejezik ki, hogy a Fourier-együtthatók kis helyre koncentrálódnak. A két mennyiség viszonyát illetően máig nem bizonyított az a sejtés, hogy az entrópia nem lehet nagyobb, mint a hatásfüggvény:
Entrópia-hatásfüggvény-sejtés. Létezik olyan 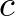 konstans, hogy minden
konstans, hogy minden 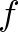 Boole-függvényre
Boole-függvényre
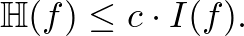
Néhány egyszerű függvény, amelyekre a sejtés igaz: például az AND (értéke pontosan akkor 1, ha a bemeneti vektor összes koordinátája 1), OR (értéke pontosan akkor 1, ha a bemeneti vektor legalább egy koordinátája 1), és egyéb alapvető logikai függvények. Ezek direkt kiszámolásánál az is kiderül, hogy a konstans legalább 4 kell legyen. A [5] cikkben olvasható, hogy az eddig belátott legjobb alsó korlát már 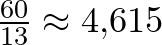 .
.
A sejtést először Kalai és Friedgut vetette fel monoton gráftulajdonságok vizsgálata közben [2]. A vizsgálataik során a sejtés állítását a hatásfüggvényre adott alsó becslésként használták volna fel. A problémával és annak különböző következményeivel sokan foglalkoztak. Gil Kalai 2007-es Terrence Tao blogjára írt bejegyzésében kitűnő áttekintést nyújt a kérdés jelentősségéről az addig ismert eredmények alapján [3]. Itt olvasható például, hogy Mansour sejtése is következne Kalai és Friedgut eredeti sejtéséből. Ez nagy vonalakban arról szól, hogy, amennyiben egy Boole-függvény „tömören reprezentálható”, akkor a Fourier-együtthatók „kis helyre koncentrálódnak”.
A sejtés véletlen függvényekre
Sok eredmény született Kalai 2007-es írása óta is a témában, például a sejtés bizonyítása különböző speciális függvényosztályokra ([5]). Mi egy eredményre szeretnénk még kitérni, miszerint véltelenül választott Boole-függvény esetén a sejtés „nagy valószínűséggel igaz”. Mit jelent ez pontosan?
Válasszunk egy véletlen  Boole-függvényt úgy, hogy minden
Boole-függvényt úgy, hogy minden  -beli ponthoz
-beli ponthoz  valószínűséggel rendelünk
valószínűséggel rendelünk 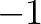 -et vagy
-et vagy 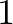 -et. Ekkor minden
-et. Ekkor minden  függvényt
függvényt 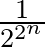 valószínűséggel kapunk. Legyenek
valószínűséggel kapunk. Legyenek  és
és 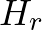 valószínűségi változók, amelyek az így választott függvény teljes hatásfüggvényét és entrópiáját jelölik. Az állítás gyakorlatilag azt mondja ki, hogy amennyiben a sejtésben
valószínűségi változók, amelyek az így választott függvény teljes hatásfüggvényét és entrópiáját jelölik. Az állítás gyakorlatilag azt mondja ki, hogy amennyiben a sejtésben 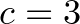 -at választunk konstansnak, akkor az előbbi módon véletlenül választott Boole-függvény nagyon kis valószínűséggel lehet egyáltalán ellenpélda. Vagyis, ha léteznek is függvények, amelyek cáfolják a sejtést
-at választunk konstansnak, akkor az előbbi módon véletlenül választott Boole-függvény nagyon kis valószínűséggel lehet egyáltalán ellenpélda. Vagyis, ha léteznek is függvények, amelyek cáfolják a sejtést 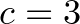 -ra, akkor azok csak nagyon (
-ra, akkor azok csak nagyon (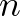 -ben exponenciálisan) kis hányadát teszik ki az össze Boole-függvénynek. Formálisan az állítás:
-ben exponenciálisan) kis hányadát teszik ki az össze Boole-függvénynek. Formálisan az állítás:
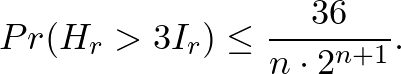
Tehát egyenletesen véletlenül választott függvényre 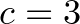 konstanssal legalább
konstanssal legalább 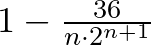 valószínűséggel teljesül az entrópia-hatásfüggvény-sejtés.
valószínűséggel teljesül az entrópia-hatásfüggvény-sejtés.
Ennek az állításnak a bizonyítása már bőven meghaladja ennek az írásnak a terjedelmi korlátait. Azonban részben azért is emeltük ki ezt az eredményt, mert bár a bizonyításban néhol megjelennek hosszabb számítások, az eddig bevezetett fogalmakon kívül nem igazán igényel magasabb szintű matematikai tudást, csupán elemi valószínűségszámítási ismereteken alapul. Akit érdekel a gondolatmenet, és nem riad vissza néhány hosszabb, de helyenként kifejezetten ötletes számolás végigolvasásától, az a levezetését teljes egészében elolvashatja [1]-ben.
Bizonyítások
Az 1. állítás bizonyítása.
(i) 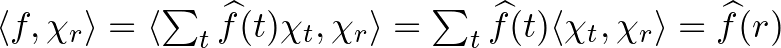 .
.
(ii) 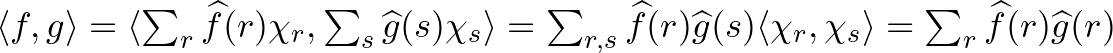 .
.
(iii) az (ii) speciális esete, amikor 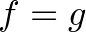 .
.
(iv) A Boole-függvények értékei 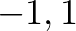 ezért (iii)-at felhasználva kapjuk az állítást.
ezért (iii)-at felhasználva kapjuk az állítást. 
A 2. állítás bizonyítása. Vegyük észre, hogy a definíció egyszerű következménye, hogy ![$I_i(f)= \mathbb{E}_x\left[\frac{(f(x)- f(x^{\oplus i}))^2}{4}\right]$](/images/stories/latexuj/2021-08/2021-08-bakospalfy/img66.png) .
.
Valóban,  értéke vagy 0, nincs változás, vagy
értéke vagy 0, nincs változás, vagy 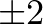 . Tehát
. Tehát 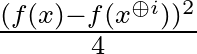 értéke pontosan akkor 1, ha
értéke pontosan akkor 1, ha 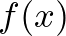 értéke változik az
értéke változik az 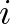 -edik koordináta előjelváltásával, és akkor 0, ha nem. Vagyis ez a mennyiség pont a nekünk szükséges esemény indikátorfüggvénye, melynek várható értéke épp a valószínűség.
-edik koordináta előjelváltásával, és akkor 0, ha nem. Vagyis ez a mennyiség pont a nekünk szükséges esemény indikátorfüggvénye, melynek várható értéke épp a valószínűség.
Most igazoljuk, hogy 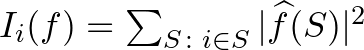 .
.
Tekintsük az  különbséget;
különbséget; 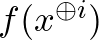 jelentése, amikor az
jelentése, amikor az 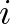 -edik koordinátát az ellenkezőjére változtatjuk. Ha vesszük
-edik koordinátát az ellenkezőjére változtatjuk. Ha vesszük 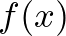 és
és 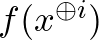 Fourier-előállítását, azon
Fourier-előállítását, azon 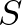 -ekhez tartozó tagok, amelyekben az
-ekhez tartozó tagok, amelyekben az 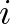 nem szerepel mind a két függvényben azonosak, tehát a különbségben kiesnek. Ha az
nem szerepel mind a két függvényben azonosak, tehát a különbségben kiesnek. Ha az  akkor
akkor 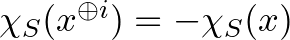 , tehát a különbségben ennek a tagnak a kétszerese szerepel. (Nem nehéz, de érdemes ellenőrizni, hogy ez a karakter mindkét formájára valóban igaz a megfelelően adott Boole-függvény esetén.) Röviden azt kaptuk, hogy
, tehát a különbségben ennek a tagnak a kétszerese szerepel. (Nem nehéz, de érdemes ellenőrizni, hogy ez a karakter mindkét formájára valóban igaz a megfelelően adott Boole-függvény esetén.) Röviden azt kaptuk, hogy

Végül
![$\displaystyle \mathbb{E}_x\left[\frac{(f(x)- f(x^{\oplus i}))^2}{4}\right]=\lef...
...n T}\widehat{f}(T)\chi_T\right\rangle=\sum_{i\in S}\vert\widehat{f}(S)\vert^2.
$](/images/stories/latexuj/2021-08/2021-08-bakospalfy/img75.png)
Az utolsó egyenlőségnél a Parseval-egyenlőséget és a karakterek ortonormáltságát használtuk. 
A 3. állítás bizonyítása.
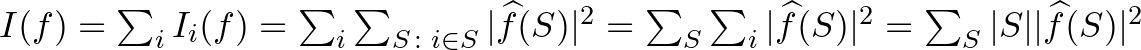 .
.
Irodalomjegyzék
- [1] Bireswar Das, Manjish Pal, and Vijay Visavaliya. The entropy influence conjecture revisited. arXiv preprint arXiv:1110.4301, 2011.
[2] Ehud Friedgut and Gil Kalai. Every monotone graph property has a sharp threshold. Proceedings of the American Mathematical Society, 124(10):2993–3002, 1996.
[3] Gil Kalai. (Gil Kalai) The entropy/influence conjecture, 2007 (accessed February 15, 2020). https://terrytao.wordpress.com/2007/08/16/gil-kalai-the-entropyinfluence-conjecture/.
[4] Gil Kalai and Shmuel Safra. Perspectives from mathematics, computer science, and economics. Computational complexity and statistical physics, page 25, 2006.
[5] Ryan O’Donnell, John Wright, and Yuan Zhou. The Fourier entropy-influence conjecture for certain classes of Boolean functions. In International Colloquium on Automata, Languages, and Programming, pages 330–341. Springer, 2011.
[6] Wikipedia. Condorcet's jury theorem -- Wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Condorcet's%20jury%20theorem&oldid=1026667834, 2021. [Online; accessed 04-August-2021].
A projekt az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósul meg (EFOP-3.6.3-VEKOP-16-2017-00002).
Bakos Bence MSc hallgató, ELTE Matematikai Intézet
Pálfy Máté doktorandusz, ELTE Matematikai Intézet









