Cikkünk első két részében azzal foglalkoztunk, hogy hány tesztelést kell végeznünk, ha adott pontossággal szeretnénk megállapítani, megbecsülni egy adott betegségben szenvedők arányát. Ehhez felidéztük a normális eloszlással való közelítést, a konfidenciaintervallum fogalmát, és bemutattuk a maximum-likelihood becslést, ami alátámasztotta azt a természetesnek tűnő becslési módszert, hogy az ismeretlen valószínűséget a bekövetkezett kísérletek arányával becsüljük. Ahogy azonban az alábbi kérdés rávilágít, még ennek az egyszerű módszernek is lehetnek hátrányai.
Kérdés. Tegyük fel, hogy egy oltás számunkra ismeretlen  valószínűséggel okoz súlyos mellékhatást. Beoltottunk (a)
valószínűséggel okoz súlyos mellékhatást. Beoltottunk (a)  ; (b)
; (b) 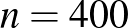 ; (c)
; (c)  embert, közülük senkinél nem tapasztaltunk ilyet. Adjunk becslést
embert, közülük senkinél nem tapasztaltunk ilyet. Adjunk becslést  értékére.
értékére.
A korábban látott egyszerű módszerrel mindhárom esetben 0 adódik  becslésére: a súlyos mellékhatás bekövetkezésének száma osztva az összes kipróbálás számával. Azonban világos, hogy a (c) esetben valójában sokkal több információnk van a
becslésére: a súlyos mellékhatás bekövetkezésének száma osztva az összes kipróbálás számával. Azonban világos, hogy a (c) esetben valójában sokkal több információnk van a  -ről, mint az (a) esetben. Kérdés, hogy ezt milyen módon tudjuk a becslésben kifejezni.
-ről, mint az (a) esetben. Kérdés, hogy ezt milyen módon tudjuk a becslésben kifejezni.
Egy lehetőség a konfidenciaintervallum, amikor például azt mondjuk, egy megfelelően választott 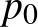 számmal, hogy a megfigyeléseink alapján
számmal, hogy a megfigyeléseink alapján  értéke legfeljebb
értéke legfeljebb 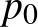 , és ezt
, és ezt 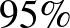 -os megbízhatósággal állítjuk, vagyis a tévedésünk valószínűsége legfeljebb
-os megbízhatósággal állítjuk, vagyis a tévedésünk valószínűsége legfeljebb 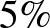 (abban az értelemben, amit cikkünk 2. részében [2] fejtettünk ki részletesebben). Azonban itt sem mindegy, hogy milyen módszert használunk: a konfidenciaintervallumról egyrészt megállapítottuk, hogy éppen a kicsi vagy egyhez közeli
(abban az értelemben, amit cikkünk 2. részében [2] fejtettünk ki részletesebben). Azonban itt sem mindegy, hogy milyen módszert használunk: a konfidenciaintervallumról egyrészt megállapítottuk, hogy éppen a kicsi vagy egyhez közeli  értékek esetén nem jól használható (hiszen nem teljesülnek annak a közelítő módszernek a feltételei, amiből kiindultunk), másrészt középpontja szintén az előfordulások aránya, vagyis a 0, az pedig nem a legoptimálisabb, ha azt mondjuk, hogy a valószínűség például
értékek esetén nem jól használható (hiszen nem teljesülnek annak a közelítő módszernek a feltételei, amiből kiindultunk), másrészt középpontja szintén az előfordulások aránya, vagyis a 0, az pedig nem a legoptimálisabb, ha azt mondjuk, hogy a valószínűség például  és
és  között van. Más módszerekkel erre a feladatra is lehet jó konfidenciaintervallumot készíteni [1], most azonban ennek ismertetése helyett egy, a korábbitól eltérő becslési módszert mutatunk be: a Bayes-becslést.
között van. Más módszerekkel erre a feladatra is lehet jó konfidenciaintervallumot készíteni [1], most azonban ennek ismertetése helyett egy, a korábbitól eltérő becslési módszert mutatunk be: a Bayes-becslést.
A Bayes-becslés nemcsak abban különbözik a korábban látott maximumlikelihood-módszertől, hogy bizonyos helyzetekben természetesebb eredményre vezet, hanem abban is, hogy lehetőséget ad az ismeretlen  paraméterre vonatkozó előzetes, a priori információik beépítésére. Ami sok esetben előny, hiszen így pontosabb becslést kaphatunk, más szempontból viszont hátrány is: ha hibás volt az eredeti feltételezésünk, az a végeredményben is megmutatkozhat. Ez azonban nem csak a Bayes-becslés sajátja, hasonló jelenséggel a statisztika számos más módszerénél is találkozunk.
paraméterre vonatkozó előzetes, a priori információik beépítésére. Ami sok esetben előny, hiszen így pontosabb becslést kaphatunk, más szempontból viszont hátrány is: ha hibás volt az eredeti feltételezésünk, az a végeredményben is megmutatkozhat. Ez azonban nem csak a Bayes-becslés sajátja, hasonló jelenséggel a statisztika számos más módszerénél is találkozunk.
1. Diszkrét a priori eloszlás
Visszatérve az eredeti kérdésünkre, nézzünk egy egyszerű példát arra, hogy a  -re vonatkozó előzetes ismereteinket hogyan fogalmazhatjuk meg, és milyen becslést kapunk eredményül. A Bayes-módszer alapötlete az, hogy az ismeretlen paramétert is véletlennek tekinti, nem csak a megfigyeléseket, vagyis, a paraméterre vonatkozó előzetes információt úgy fejezi ki, hogy megmondja, hogy a paraméter egyes értékeit vagy értéktartományait mennyire tartja valószínűnek.
-re vonatkozó előzetes ismereteinket hogyan fogalmazhatjuk meg, és milyen becslést kapunk eredményül. A Bayes-módszer alapötlete az, hogy az ismeretlen paramétert is véletlennek tekinti, nem csak a megfigyeléseket, vagyis, a paraméterre vonatkozó előzetes információt úgy fejezi ki, hogy megmondja, hogy a paraméter egyes értékeit vagy értéktartományait mennyire tartja valószínűnek.
A példa kedvéért tegyük fel, hogy az előzetes információnk szerint a súlyos mellékhatás valószínűsége, vagyis  egyenletes eloszlású a
egyenletes eloszlású a ![$[0,1]$](/images/stories/latexuj/2021-02/2021-02-backhauszagnesmennyiteszteljunk3/img10.png) intervallumon, és tegyük fel azt is, hogy egyelőre
intervallumon, és tegyük fel azt is, hogy egyelőre  -nek csak a tizedesre kerekített értékére vagyunk kíváncsiak. Legyenek tehát
-nek csak a tizedesre kerekített értékére vagyunk kíváncsiak. Legyenek tehát  lehetséges értékei 0,
lehetséges értékei 0,  ,
, 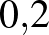 ,
,  ,
, 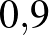 , és mindegyiknek
, és mindegyiknek 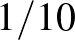 a valószínűsége. Úgy is mondhatjuk, hogy a
a valószínűsége. Úgy is mondhatjuk, hogy a  paraméter a priori eloszlása egyenletes eloszlás a 0,
paraméter a priori eloszlása egyenletes eloszlás a 0,  ,
, 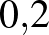 ,
,  ,
, 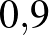 számokon.
számokon.
A kérdés (a) esetében  ember közül egyiknél sem jelentkezett súlyos mellékhatás. Ha például
ember közül egyiknél sem jelentkezett súlyos mellékhatás. Ha például 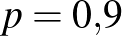 lenne, akkor várhatóan
lenne, akkor várhatóan 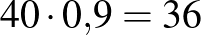 embernél lép fel ilyen, annak valószínűsége, hogy senkinél nem jelentkezik, nagyon-nagyon kicsi:
embernél lép fel ilyen, annak valószínűsége, hogy senkinél nem jelentkezik, nagyon-nagyon kicsi: 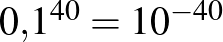 , ez nagyságrendileg annak valószínűségével egyezik meg, mint hogy öt egymást követő héten öttalálatosunk lesz a lottón. Ha viszont
, ez nagyságrendileg annak valószínűségével egyezik meg, mint hogy öt egymást követő héten öttalálatosunk lesz a lottón. Ha viszont 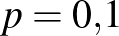 , akkor már csak várhatóan 4 embernél lép fel súlyos mellékhatás, a 0 érték sem ennyire elképzelhetetlen: a 0 megfigyelés valószínűsége
, akkor már csak várhatóan 4 embernél lép fel súlyos mellékhatás, a 0 érték sem ennyire elképzelhetetlen: a 0 megfigyelés valószínűsége 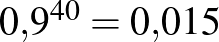 , lényegesen nagyobb az előzőnél. Ez arra utal, hogy bár előzetesen azt feltételeztük, hogy a
, lényegesen nagyobb az előzőnél. Ez arra utal, hogy bár előzetesen azt feltételeztük, hogy a  és
és 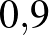 egyformán valószínűek, a megfigyelések alapján ezt újragondolva a
egyformán valószínűek, a megfigyelések alapján ezt újragondolva a  -et sokkal valószínűbbnek gondolhatjuk, mint a
-et sokkal valószínűbbnek gondolhatjuk, mint a 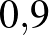 -et. Arról nem is beszélve, hogy a
-et. Arról nem is beszélve, hogy a 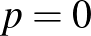 esetén biztos, hogy senkinél nem tapasztalunk súlyos mellékhatást, így ez még valószínűbbnek tűnik. A maximumlikelihood-módszer ez alapján az érvelés alapján meg is állna, és a lehetséges tíz érték közül a
esetén biztos, hogy senkinél nem tapasztalunk súlyos mellékhatást, így ez még valószínűbbnek tűnik. A maximumlikelihood-módszer ez alapján az érvelés alapján meg is állna, és a lehetséges tíz érték közül a 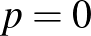 -t választaná, hiszen ebben az esetben a legnagyobb annak valószínűsége, amit megfigyeltünk. A Bayes-módszer pedig pontosan kiszámítja, hogy a megfigyelések után melyik értéket mennyire tartjuk valószínűnek, méghozzá a feltételes valószínűség fogalma alapján. Hiszen bekövetkezett az az esemény, hogy 40 ember közül senkinél nem tapasztalunk súlyos mellékhatást, így az „új” valószínűségeket erre vonatkozóan, feltételes valószínűségként tudjuk leírni.
-t választaná, hiszen ebben az esetben a legnagyobb annak valószínűsége, amit megfigyeltünk. A Bayes-módszer pedig pontosan kiszámítja, hogy a megfigyelések után melyik értéket mennyire tartjuk valószínűnek, méghozzá a feltételes valószínűség fogalma alapján. Hiszen bekövetkezett az az esemény, hogy 40 ember közül senkinél nem tapasztalunk súlyos mellékhatást, így az „új” valószínűségeket erre vonatkozóan, feltételes valószínűségként tudjuk leírni.
Legyen tehát 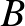 az az esemény, hogy 40 ember közül senkinél nem volt súlyos mellékhatás,
az az esemény, hogy 40 ember közül senkinél nem volt súlyos mellékhatás, 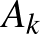 pedig az az esemény, hogy
pedig az az esemény, hogy  értéke
értéke 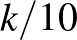 (itt
(itt  a lehetséges értékek). Ekkor a
a lehetséges értékek). Ekkor a
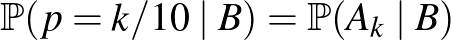
feltételes valószínűség mondja meg, hogy a megfigyelések alapján a  értéket mennyire tartjuk valószínűnek. A feltételes valószínűség definíciója (lásd például [3]) alapján:
értéket mennyire tartjuk valószínűnek. A feltételes valószínűség definíciója (lásd például [3]) alapján:
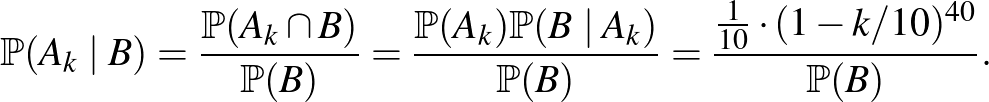 |
(1) |
Itt a számláló annak a valószínűsége, hogy  értéke
értéke 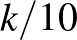 és a 40 ember közül senkinél sem jelenkezett súlyos mellékhatás. Az előbbi valószínűsége
és a 40 ember közül senkinél sem jelenkezett súlyos mellékhatás. Az előbbi valószínűsége 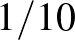 volt minden lehetséges
volt minden lehetséges 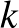 értékre az a priori eloszlás szerint, ha pedig
értékre az a priori eloszlás szerint, ha pedig 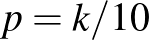 , akkor 40 független kísérletben
, akkor 40 független kísérletben 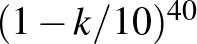 annak a valószínűsége, hogy egyszer sem lép fel súlyos mellékhatás.
annak a valószínűsége, hogy egyszer sem lép fel súlyos mellékhatás.
Kérdés, hogy a nevezőben 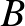 valószínűségét hogyan írhatjuk fel. Vegyük észre, hogy ha
valószínűségét hogyan írhatjuk fel. Vegyük észre, hogy ha  értéke ismert, akkor annak valószínűségét, hogy
értéke ismert, akkor annak valószínűségét, hogy 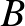 bekövetkezik, könnyen ki tudtuk számolni. Vagyis a
bekövetkezik, könnyen ki tudtuk számolni. Vagyis a  feltételes valószínűségeket meg tudtuk határozni. Mivel pedig az
feltételes valószínűségeket meg tudtuk határozni. Mivel pedig az 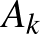 események közül pontosan az egyik következik be, és a valószínűségeiket is ismerjük, a teljes valószínűség tételét (lásd például [3]) alkalmazva:
események közül pontosan az egyik következik be, és a valószínűségeiket is ismerjük, a teljes valószínűség tételét (lásd például [3]) alkalmazva:
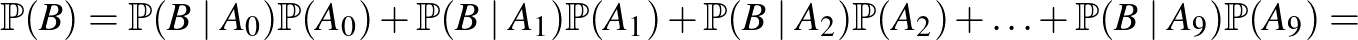 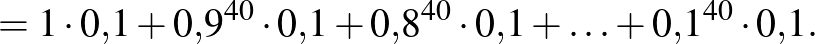 |
(2) |
Ezt az (1) egyenlettel összevetve megkapjuk a  lehetséges értékeinek a megfigyelések alapján számolt feltételes, a posteriori valószínűségét:
lehetséges értékeinek a megfigyelések alapján számolt feltételes, a posteriori valószínűségét:
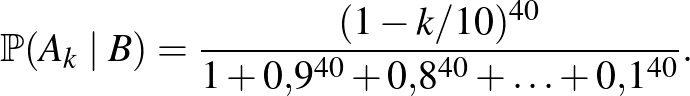
Ugyanehhez jutottunk volna Bayes tételének alkalmazásával is, innen adódik a módszer neve. A számításokhoz visszatérve, például a 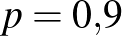 feltételes valószínűsége arra vonatkozóan, hogy az
feltételes valószínűsége arra vonatkozóan, hogy az  ember közül senkinél nem jelentkezett súlyos mellékhatás:
ember közül senkinél nem jelentkezett súlyos mellékhatás:
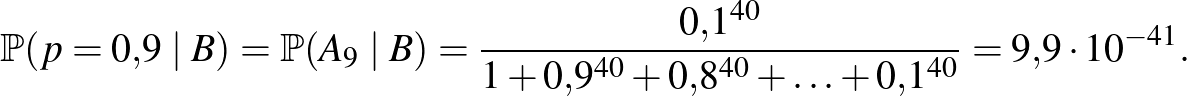
Ugyanez 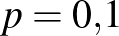 esetén:
esetén:
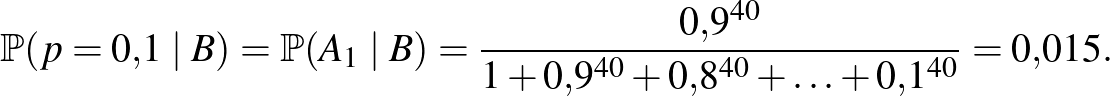
Tehát, az, hogy a  esemény bekövetkezése a
esemény bekövetkezése a  érték esetén sokkal valószínűbb, mint
érték esetén sokkal valószínűbb, mint 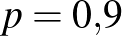 esetén (
esetén ( , illetve
, illetve  , ahogy korábban láttuk), azt eredményezi, hogy a
, ahogy korábban láttuk), azt eredményezi, hogy a 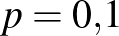 érték megfigyelések utáni, a posteriori valószínűsége sokkal nagyobb, mint a
érték megfigyelések utáni, a posteriori valószínűsége sokkal nagyobb, mint a 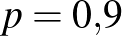 értéké. Ilyen módon tudjuk újragondolni az egyes lehetséges értékek valószínűségéről alkotott elképzeléseinket a kísérletek elvégzése alapján – és ebben az esetben még csak az sem kellett, hogy a
értéké. Ilyen módon tudjuk újragondolni az egyes lehetséges értékek valószínűségéről alkotott elképzeléseinket a kísérletek elvégzése alapján – és ebben az esetben még csak az sem kellett, hogy a  -ről előzetesen nagyon pontos ismeretekkel rendelkezzünk.
-ről előzetesen nagyon pontos ismeretekkel rendelkezzünk.
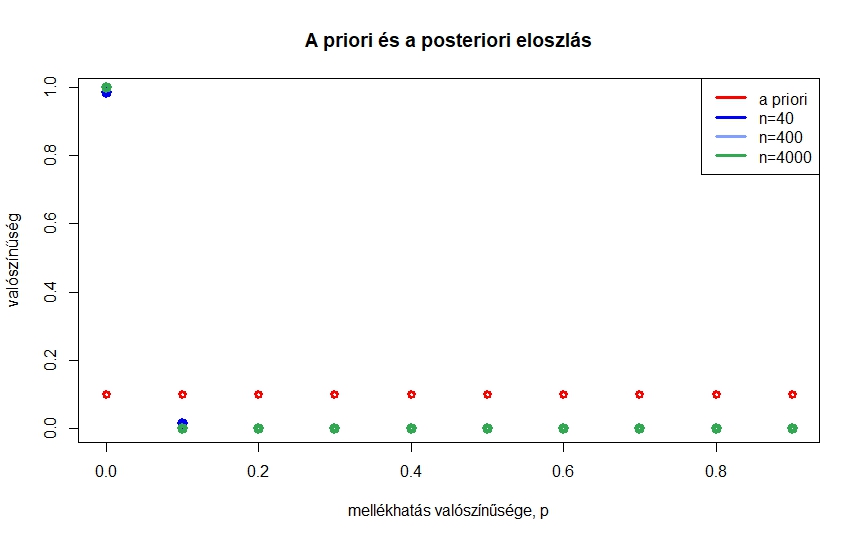
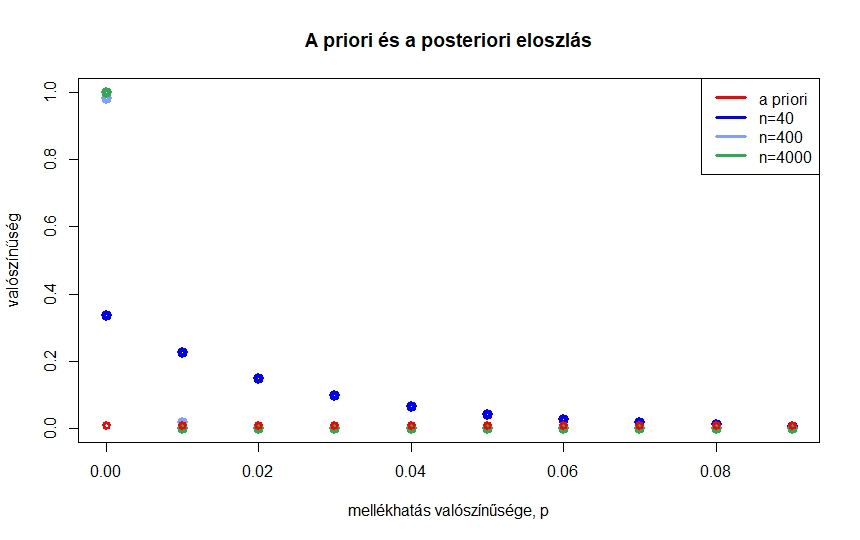
1. ábra. A 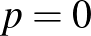 ,
,  ,
,  ,
,  értékek valószínűsége az előzetes elképzelés szerint, illetve arra feltételesen, hogy
értékek valószínűsége az előzetes elképzelés szerint, illetve arra feltételesen, hogy  , 400, 4000 kísérletből egyszer sem volt súlyos mellékhatás
, 400, 4000 kísérletből egyszer sem volt súlyos mellékhatás
Kérdés, mi történik, ha a kísérletek számát növeljük, de továbbra is azt feltételezzük, hogy senkinél nem volt súlyos mellékhatás. Az 1. ábrán azt láthatjuk, hogy  , 400, 4000 esetén hogyan alakulnak ezek a valószínűségek. Mivel az értékek egymáshoz közeliek, nézzük meg ezt egy táblázat segítségével is. A táblázatban kerekített értékek szerepelnek, ha pedig
, 400, 4000 esetén hogyan alakulnak ezek a valószínűségek. Mivel az értékek egymáshoz közeliek, nézzük meg ezt egy táblázat segítségével is. A táblázatban kerekített értékek szerepelnek, ha pedig  , még ezeknél is kisebb értékeket kapunk. Összességében azt láthatjuk, hogy minél nagyobb a kísérletek száma, annál közelebb van a 0 a posteriori valószínűsége az 1-hez, és hogy 400 kísérlet elég ahhoz, hogy a
, még ezeknél is kisebb értékeket kapunk. Összességében azt láthatjuk, hogy minél nagyobb a kísérletek száma, annál közelebb van a 0 a posteriori valószínűsége az 1-hez, és hogy 400 kísérlet elég ahhoz, hogy a  és nagyobb értékek a posteriori valószínűsége elhanyagolhatóvá váljon.
és nagyobb értékek a posteriori valószínűsége elhanyagolhatóvá váljon.
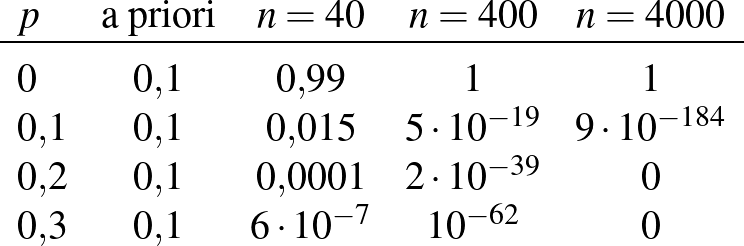
Egy másik, talán még fontosabb kérdés az, hogy mi történik, ha  lehetséges értékeinek halmazát bővítjük. Eddig összesen 10-féle lehetőséget engedtünk meg, a táblázatból pedig arra következtethetünk, hogy a 0 sokkal valószínűbb, mint a
lehetséges értékeinek halmazát bővítjük. Eddig összesen 10-féle lehetőséget engedtünk meg, a táblázatból pedig arra következtethetünk, hogy a 0 sokkal valószínűbb, mint a  vagy a még nagyobb értékek. Ehhez még a Bayes-becslés sem feltétlenül kellett volna, ha azonban több lehetséges értéket is megengedünk, akkor pontosabb információhoz is juthatunk.
vagy a még nagyobb értékek. Ehhez még a Bayes-becslés sem feltétlenül kellett volna, ha azonban több lehetséges értéket is megengedünk, akkor pontosabb információhoz is juthatunk.
Módosítsuk tehát az a priori eloszlást, úgy, hogy nem tizedekre, hanem századokra kerekített  valószínűségeket hasonlíthassunk össze. A lehetséges értékek legyenek 0,
valószínűségeket hasonlíthassunk össze. A lehetséges értékek legyenek 0,  ,
, 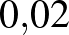 ,
,  ,
, 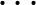 ,
, 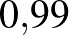 , és továbbra is legyen mindegyiknek azonos,
, és továbbra is legyen mindegyiknek azonos, 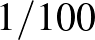 a valószínűsége az előzetes feltételezésünk szerint. Legyen most
a valószínűsége az előzetes feltételezésünk szerint. Legyen most 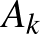 az az esemény, hogy a
az az esemény, hogy a  értéke
értéke 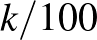 (itt
(itt 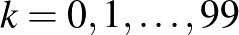 . A (2) egyenlethez hasonlóan, ha
. A (2) egyenlethez hasonlóan, ha 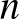 kísérletből egyik alkalommal sem lépett fel súlyos mellékhatás:
kísérletből egyik alkalommal sem lépett fel súlyos mellékhatás:
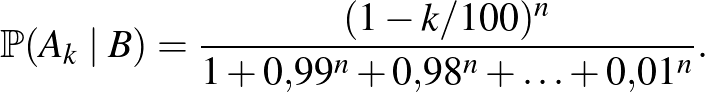 |
(3) |
Tehát ha például  kísérletből egyszer sem volt súlyos mellékhatás, akkor
kísérletből egyszer sem volt súlyos mellékhatás, akkor
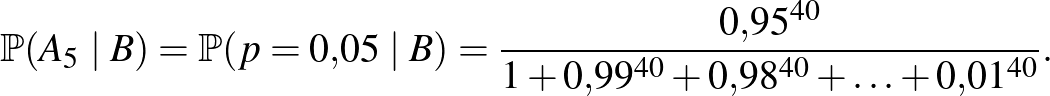
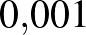 ,
, 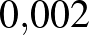 ,
,  ,
, 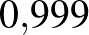 ezer lehetséges értéknek ad azonos valószínűségeket).
ezer lehetséges értéknek ad azonos valószínűségeket).
 |
 |
2. ábra. Az egyes 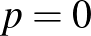 ,
,  ,
, 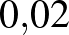 ,
,  ,
, 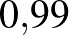 (bal oldal), illetve
(bal oldal), illetve 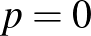 ,
, 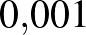 ,
, 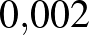 ,
,  ,
, 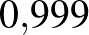 értékek valószínűsége az előzetes elképzelés szerint, illetve arra feltételesen, hogy
értékek valószínűsége az előzetes elképzelés szerint, illetve arra feltételesen, hogy  , 400, 4000 kísérletből egyszer sem volt súlyos mellékhatás
, 400, 4000 kísérletből egyszer sem volt súlyos mellékhatás
Ahogy a 2. ábrán látjuk, egyrészt, az a posteriori eloszlás szerint minden esetben a kisebb  -k lesznek nagyobb valószínűségűek. Ugyanakkor azt is láthatjuk, hogy a posteriori eloszlás függ az előzetes feltételezésünktől, vagyis attól, hogy eredetileg milyen lehetséges értékeket tekintettünk. Például ha
-k lesznek nagyobb valószínűségűek. Ugyanakkor azt is láthatjuk, hogy a posteriori eloszlás függ az előzetes feltételezésünktől, vagyis attól, hogy eredetileg milyen lehetséges értékeket tekintettünk. Például ha  , akkor csak azt állapíthatjuk meg, hogy a
, akkor csak azt állapíthatjuk meg, hogy a 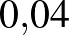 -nél nagyobb értékek nem túl valószínűek, ha
-nél nagyobb értékek nem túl valószínűek, ha 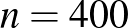 , akkor ez a
, akkor ez a  -nél nagyobb értékekre is elmondható – azzal valamennyire összhangban, hogy
-nél nagyobb értékekre is elmondható – azzal valamennyire összhangban, hogy 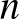 kísérletből nem várható, hogy
kísérletből nem várható, hogy 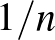 -nél nagyobb pontossággal meghatározzuk a kérdéses valószínűséget.
-nél nagyobb pontossággal meghatározzuk a kérdéses valószínűséget.
2. Folytonos a priori eloszlás
Az eddigi gondolatmenettel kapcsolatban felvetődik, hogy nem tudnánk-e előzetes és utólagos kerekítések nélkül becsülni  -t, tizedektől, századoktól függetlenül, hogy a kerekítésektől ne függjön az eloszlás.
-t, tizedektől, századoktól függetlenül, hogy a kerekítésektől ne függjön az eloszlás.
Ehhez tegyük fel, hogy a súlyos mellékhatás kialakulásának  valószínűségéről azt feltételezzük előzetesen, hogy egyenletes eloszlású a
valószínűségéről azt feltételezzük előzetesen, hogy egyenletes eloszlású a ![$[0,1]$](/images/stories/latexuj/2021-02/2021-02-backhauszagnesmennyiteszteljunk3/img10.png) intervallumon. Ilyenkor tehát már végtelen sok lehetséges érték van, és például a korábban kiszámított
intervallumon. Ilyenkor tehát már végtelen sok lehetséges érték van, és például a korábban kiszámított 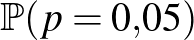 valószínűségre nullát kapnánk, annak megfelelően, hogy előzetesen minden konkrét értéknek 0 a valószínűsége. Ha azonban újra megnézzük a (3) egyenletet, azt láthatjuk, hogy a jobb oldalának tudunk értelmet adni. A számlálóban annak valószínűsége szerepel, hogy feltéve, hogy
valószínűségre nullát kapnánk, annak megfelelően, hogy előzetesen minden konkrét értéknek 0 a valószínűsége. Ha azonban újra megnézzük a (3) egyenletet, azt láthatjuk, hogy a jobb oldalának tudunk értelmet adni. A számlálóban annak valószínűsége szerepel, hogy feltéve, hogy  értéke
értéke 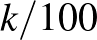 , mennyi a valószínűsége, hogy az
, mennyi a valószínűsége, hogy az 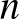 kísérletből egy sem következik be, ez nem más, mint
kísérletből egy sem következik be, ez nem más, mint 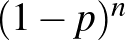 . A nevezőbe annak valószínűsége került, hogy az
. A nevezőbe annak valószínűsége került, hogy az 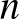 kísérletből egy sem következik be. Ezt a teljes valószínűség tételének egy általánosabb változata alapján írhatjuk fel, értéke (az előző összegek analógiájára)
kísérletből egy sem következik be. Ezt a teljes valószínűség tételének egy általánosabb változata alapján írhatjuk fel, értéke (az előző összegek analógiájára) 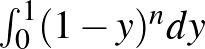 . Amit pedig megkapunk így, az nem más, mint az a posteriori sűrűségfüggvény:
. Amit pedig megkapunk így, az nem más, mint az a posteriori sűrűségfüggvény:
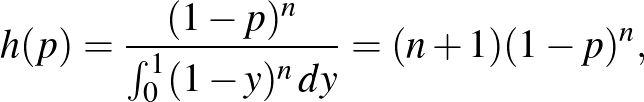
ha a nevezőben szereplő integrált is kiszámítjuk.
Ezt a következőre használhatjuk fel. Ha meg szeretnénk tudni, hogy egy ![$A\subseteq [0,1]$](/images/stories/latexuj/2021-02/2021-02-backhauszagnesmennyiteszteljunk3/img59.png) (megfelelő) halmazba mennyi valószínűséggel esik
(megfelelő) halmazba mennyi valószínűséggel esik  értéke arra feltételesen, hogy
értéke arra feltételesen, hogy 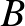 bekövetkezett, vagyis nem volt súlyos mellékhatás egyik esetben sem, akkor így számolhatunk:
bekövetkezett, vagyis nem volt súlyos mellékhatás egyik esetben sem, akkor így számolhatunk:

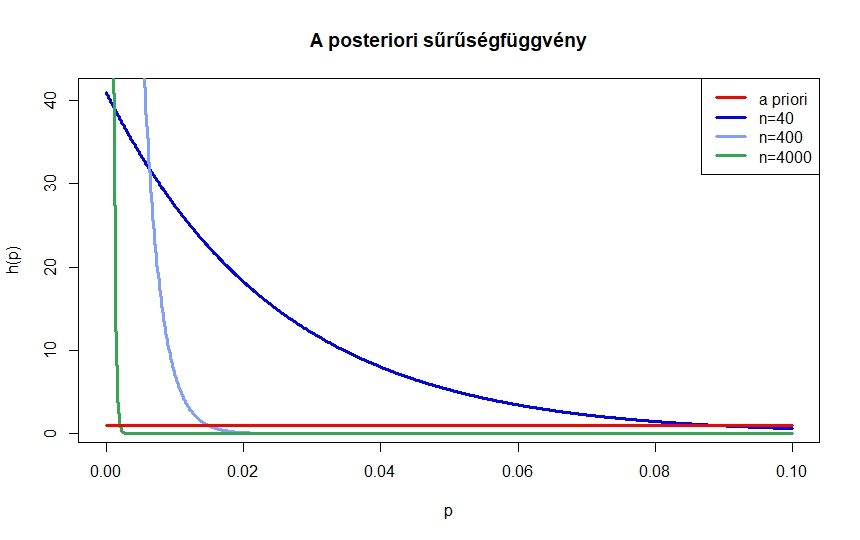
3.ábra. Az a posteriori sűrűségfüggvények arra feltételesen, hogy  , 400, 4000 kísérletből egyszer sem volt súlyos mellékhatás
, 400, 4000 kísérletből egyszer sem volt súlyos mellékhatás
A 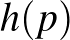 függvényeket
függvényeket  , 400 és 4000 kísérlet esetén a 3. ábrán láthatjuk. A sűrűségfüggvény nagy értékei jelzik azokat a tartományokat, ahova
, 400 és 4000 kísérlet esetén a 3. ábrán láthatjuk. A sűrűségfüggvény nagy értékei jelzik azokat a tartományokat, ahova  nagy valószínűséggel esik. Tehát az
nagy valószínűséggel esik. Tehát az  kísérlet elégnek tűnik ahhoz, hogy megállapítsuk, hogy
kísérlet elégnek tűnik ahhoz, hogy megállapítsuk, hogy  nagy valószínűséggel nem több
nagy valószínűséggel nem több  -nál, de azt már nem mondhatjuk, hogy
-nál, de azt már nem mondhatjuk, hogy  kisebb lesz, mint
kisebb lesz, mint 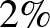 , hiszen a sűrűségfüggvény alatti terület nagyjából fele a
, hiszen a sűrűségfüggvény alatti terület nagyjából fele a 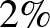 -tól jobbra esik. Az
-tól jobbra esik. Az 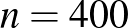 kísérletből arra juthatunk, hogy
kísérletből arra juthatunk, hogy  nagy valószínűséggel 0 és
nagy valószínűséggel 0 és 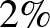 között van, míg
között van, míg  esetén azt is mondhatjuk, hogy
esetén azt is mondhatjuk, hogy  nagy valószínűséggel kisebb egy ezrednél, legalábbis az a posteriori eloszlás szerint.
nagy valószínűséggel kisebb egy ezrednél, legalábbis az a posteriori eloszlás szerint.
3. A Bayes-becslés
Az eddigi számításokból a leglényegesebb még nem derült ki: mi is lesz a Bayes-becslés, vagyis az a szám, amiről azt állíthatjuk a megfigyeléseink alapján, hogy közel van a valódi  -hez, legalábbis valamilyen értelemben, például elég nagy valószínűséggel.
-hez, legalábbis valamilyen értelemben, például elég nagy valószínűséggel.
Most tehát végeredményképpen nem egy eloszlást és nem egy sűrűségfüggvényt szeretnénk, ami megmondja, hogy  milyen tartományokba milyen valószínűségekkel esik, hanem egyetlen számot. Esetleg ezt a számot sorsolhatjuk véletlenül: mondhatjuk, hogy a
milyen tartományokba milyen valószínűségekkel esik, hanem egyetlen számot. Esetleg ezt a számot sorsolhatjuk véletlenül: mondhatjuk, hogy a  -nek olyan véletlen számot választunk, amit a
-nek olyan véletlen számot választunk, amit a 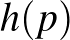 sűrűségfüggvény által leírt eloszlásból sorsolunk. Ez azonban még nem túlságosan stabil, az eljárást ismételve egészen más eredményeket kaphatunk. Ha azonban sokszor kisorsolnánk
sűrűségfüggvény által leírt eloszlásból sorsolunk. Ez azonban még nem túlságosan stabil, az eljárást ismételve egészen más eredményeket kaphatunk. Ha azonban sokszor kisorsolnánk  -t a
-t a 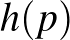 sűrűségfüggvény által leírt eloszlásból, majd átlagot vennénk, az már egyetlen szám lenne, és stabil, a mintától függ, de további véletlenítéstől nem. A nagy számok törvényéből (lásd például: [3]) tudjuk, hogy az átlag az eloszlás várható értékéhez konvergál, ha a mintaelemszámmal végtelenhez tartunk, és megfelelő feltételek teljesülnek. Tehát, ha így gondolkodunk, akkor lényegében az a posteriori eloszlás várható értéke lesz a tippünk.
sűrűségfüggvény által leírt eloszlásból, majd átlagot vennénk, az már egyetlen szám lenne, és stabil, a mintától függ, de további véletlenítéstől nem. A nagy számok törvényéből (lásd például: [3]) tudjuk, hogy az átlag az eloszlás várható értékéhez konvergál, ha a mintaelemszámmal végtelenhez tartunk, és megfelelő feltételek teljesülnek. Tehát, ha így gondolkodunk, akkor lényegében az a posteriori eloszlás várható értéke lesz a tippünk.
Ez valójában a leggyakrabban alkalmazott módszer a Bayes-becslésre, az a posteriori eloszlás alapján. Az átlagoláson kívül még egy érv szól mellette: be lehet látni, hogy ez a várható érték az a becslés, amely bizonyos értelemben minimalizálja a tippünk és az igazi érték távolságát. Ez a minimalizáló tulajdonság az, ami alapján a Bayes-becslést meg szokták határozni.
Lássuk, mit ad ez a konkrét esetekben. Az a posteriori sűrűségfüggvényből a szokásos módon számíthatjuk ki a várható értéket, ez lesz tehát becslésünk  -re:
-re:


Tehát ha 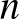 független kísérletből egyszer sem következik be a súlyos mellékhatás, és a
független kísérletből egyszer sem következik be a súlyos mellékhatás, és a ![$[0,1]$](/images/stories/latexuj/2021-02/2021-02-backhauszagnesmennyiteszteljunk3/img10.png) intervallumon egyenletes eloszlás az előzetes feltevés, akkor a súlyos mellékhatás valószínűségére adott becslésünk
intervallumon egyenletes eloszlás az előzetes feltevés, akkor a súlyos mellékhatás valószínűségére adott becslésünk 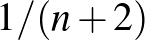 . A korábban vizsgált esetekben ez így alakul:
. A korábban vizsgált esetekben ez így alakul:
![\begin{displaymath}\begin{array}{lcccc}n & 40 & 400 & 4000\\ \hline\\ [-10pt]\hat p & 2{,}39\% & 0{,}249\% &0{,}025\%.\end{array}\end{displaymath}](/images/stories/latexuj/2021-02/2021-02-backhauszagnesmennyiteszteljunk3/img67.png)
Másképpen, ez azt is jelenti, hogy ha például azt szeretnénk bizonyítani, hogy a súlyos mellékhatás valószínűsége legfeljebb 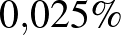 , akkor legalább 4000 vizsgálatot kell végeznünk. Általában, ha a súlyos mellékhatás valószínűsége legfeljebb
, akkor legalább 4000 vizsgálatot kell végeznünk. Általában, ha a súlyos mellékhatás valószínűsége legfeljebb 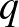 lehet, akkor legalább
lehet, akkor legalább
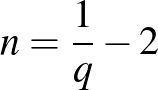
vizsgálatra van szükség. Ugyanis ebből a szempontból az, hogy egyetlen esetben sem tapasztalunk mellékhatást, a lehető legjobb eset: ha néhány esetben mellékhatás következik be, akkor  értéke nagyobb lesz.
értéke nagyobb lesz.
A számolás részleteit mellőzve, a fentihez hasonló érveléssel azt lehet belátni, hogy ha 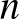 kísérletből
kísérletből 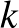 esetben tapasztalunk súlyos mellékhatást, akkor
esetben tapasztalunk súlyos mellékhatást, akkor
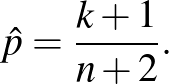
Ahogy a bevezetésben említettük, ez a becslés függ az előzetes feltevésünktől is, vagyis az a priori eloszlástól. Erre is nézzünk egy példát. Eddig abból indultunk ki, hogy  egyenletes eloszlású a
egyenletes eloszlású a ![$[0{,}1]$](/images/stories/latexuj/2021-02/2021-02-backhauszagnesmennyiteszteljunk3/img73.png) intervallumon. Tegyük fel először, hogy előzetesen is sejtjük, hogy
intervallumon. Tegyük fel először, hogy előzetesen is sejtjük, hogy  kicsi, az a priori sűrűségfüggvény legyen például
kicsi, az a priori sűrűségfüggvény legyen például 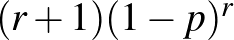 , ahol
, ahol  tetszőleges. Ez ugyanis a 0 körül nagyobb értékeket vesz fel, mint az 1 körül. Nézzünk meg azt is, hogy ha előzetesen éppen hogy rossz a feltevésünk, vagyis a 0 körüli értékek a kevéssé valószínűek, akkor mennyire „javul meg” a becslés a bayes-i módszerrel. Ehhez például legyen a priori sűrűségfüggvény
tetszőleges. Ez ugyanis a 0 körül nagyobb értékeket vesz fel, mint az 1 körül. Nézzünk meg azt is, hogy ha előzetesen éppen hogy rossz a feltevésünk, vagyis a 0 körüli értékek a kevéssé valószínűek, akkor mennyire „javul meg” a becslés a bayes-i módszerrel. Ehhez például legyen a priori sűrűségfüggvény  .
.

Itt tehát az látható, hogy az előzetes feltevés lényeges hatással van a becslésre, a becsült értékek között nagyságrendi eltérést is láthatunk a  esetben. A „tipikus” esetben persze az történik, hogy
esetben. A „tipikus” esetben persze az történik, hogy 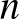 értékét növelve a bekövetkezett kísérletek száma,
értékét növelve a bekövetkezett kísérletek száma, 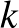 is növekszik, így ha
is növekszik, így ha 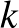 és
és 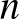 elég nagy
elég nagy  -hez képest, akkor a három érték már majdnem ugyanakkora lesz. Mindenesetre ez a példa is mutatja, hogy ha a minta nagyon másképpen viselkedik, mint azt az előzetes feltételezés szerint várnánk, akkor a Bayes-becslés megtévesztő eredményekre is vezethet: ha 40 kísérletből egy sem sikerül, a
-hez képest, akkor a három érték már majdnem ugyanakkora lesz. Mindenesetre ez a példa is mutatja, hogy ha a minta nagyon másképpen viselkedik, mint azt az előzetes feltételezés szerint várnánk, akkor a Bayes-becslés megtévesztő eredményekre is vezethet: ha 40 kísérletből egy sem sikerül, a 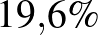 nem éppen a legjobb becslésnek tűnik a valószínűségre. Ugyanakkor az
nem éppen a legjobb becslésnek tűnik a valószínűségre. Ugyanakkor az  kísérlet ahhoz már elég, hogy akkor is jónak mondható eredményt kapjunk, ha előzetesen kevés információnk volt
kísérlet ahhoz már elég, hogy akkor is jónak mondható eredményt kapjunk, ha előzetesen kevés információnk volt  -ről, és egyenletes eloszlásúnak tételeztük fel.
-ről, és egyenletes eloszlásúnak tételeztük fel.
4. Összefoglalás
Ahogy láttuk, a Bayes-becslés módszerében lényeges különbség a korábbiakhoz képest, hogy itt magát a paramétert is egy véletlen számnak tekintjük, és van egy előzetes elképzelésünk arról, hogy milyen értékeket milyen valószínűséggel vesz fel (diszkrét a priori eloszlás), illetve az egyes tartományokba milyen valószínűséggel esik (a priori sűrűségfüggvény). Amit kiszámítunk, az az, hogy ezek a valószínűségek hogyan alakulnak, ha a megfigyeléseinket mint feltételeket beépítjük (a posteriori eloszlás), így megkapjuk, hogy a megfigyelések alapján melyek lesznek a paraméter valószínű és kevéssé valószínű értékei, értéktartományai. Ha egyetlen számmal írjuk le a becslést, akkor ennek az eloszlásnak a várható értékét vesszük, ez adja a becslésünket, ami természetesen függ az előzetes feltételezéstől is. Minél pontosabb az előzetes feltételezésünk, annál kevesebb megfigyelés elég a pontos becsléshez, és fordítva, ha a mintaelemszám elég nagy, akkor egy nem túl pontos előzetes feltételezésből is jó eredményekhez juthatunk. A téma részletesebb megismerésében például a [4,5] könyvek segíthetnek.
Irodalomjegyzék
- [1] Douglas Altman, David Machin, Trevor Bryant, Martin Gardner, Statistics with Confidence: Confidence Intervals and Statistical Guidelines. Second Edition, John Wiley & Sons, New York, 2000.
[2] Backhausz Ágnes, Simon L. Péter, Mennyit teszteljünk? 2. rész, Érintő, 2020. szeptember. https://ematlap.hu/tudomany-tortenet-2020-12/992-mennyit-teszteljunk-2-v3
[3] Csiszár Villő, Valószínűségszámítás 1. http://csvillo.web.elte.hu/mtval/jegyzet.pdf
[4] Allen B. Downey, Think Bayes: Bayesian Statistics in Python. First edition, O'Reilly, Sebastopol, 2012.
[5] Peter M. Lee, Bayesian Statistics: An Introduction. John Wiley & Sons, Chicester, 2012.
Backhausz Ágnes
Eötvös Loránd Tudományegyetem, Matematikai Intézet









