Mi is…a perkoláció?

A perkoláció a statisztikus fizika és a modern valószínűségszámítás egyik legegyszerűbben definiálható, ugyanakkor nagyon mély problémákhoz és általános tanulságokhoz vezető modellje, amiben fázisátmenet történik; hogy ez mit jelent, hamarosan elmagyarázzuk.

A modell minden véges vagy végtelen gráfon értelmezhető, és két alapváltozata van: élperkolációban a gráf éleit egymástól függetlenül ugyanakkora $p$ valószínűséggel nyíltnak, illetve $1-p$ -vel zártnak sorsoljuk ki; csúcsperkolációban a csúcsokat sorsoljuk nyíltnak vagy zártnak. A két változatban az alapjelenségek ugyanazok, így egyelőre beszéljünk csak az élperkolációról. A zárt élekre úgy gondolunk, mint amiket kitöröltünk, és az érdekel minket, hogy a megmaradó nyílt éleken keresztül honnan hová lehet eljutni, azaz mik a megmaradt véletlen gráf összefüggőségi komponensei, más szóval fürtjei.

1. ábra (Készítette: Nagy Marcell)

Mind a tárgy története, mind a tanulságok szempontjából egy különösen fontos eset, amikor az alapgráf a $\mathbb{Z}^2$ négyzetrács. (Az ábrán $p=0.25$ , 0.5, $0.75$ értékekkel; a négyzetben a legnagyobb fürt pirossal kiemelve.) Egy alapvető kérdés: mi a valószínűsége annak, hogy az $o$ origóból vezet az $S_n:=[-n,n]^2$ négyzeten kívülre egy nyílt út, azaz olyan út, aminek minden éle nyílt? Ezt a kérdést Broadbent vetette fel 1954-ben egy Monte Carlo-módszereknek szentelt szimpóziumon, majd Hammersleyvel közösen folytatta a kérdés vizsgálatát. Ők egy véletlen közeg modelljeként tekintettek a perkolációra, amiben $\mathbb{Z}^2$ élei mint lehetséges csatornák jelennek meg, amiken keresztül valamilyen folyadék vagy gáz terjedhet, feltéve, hogy az adott csatorna ehhez elég széles (ennek felel meg, hogy a csatornát képviselő él nyitva áll), míg ha egy adott csatorna túl szűk, akkor rajta keresztül nem halad folyadék (ekkor lesz a hozzá tartozó él zárt). Ebben a modellben a folyadék mindenhová eljut, ahova a fenti szabályok engedik, a véletlenszerűség tehát nem a folyadék viselkedésében jelenik meg, hanem a környezetében, amiben mozog.

Ha az $S_n$ négyzetet egyre nagyobbnak vesszük, akkor, ahogy $n \rightarrow \infty$ , a következő kérdéshez érkezünk: „Mennyi a valószínűsége annak, hogy $o$ -ból indul végtelen nyílt út, azaz, hogy az $o$ fürtje végtelen?” Ezt az eseményt szokás perkolációnak is nevezni; ha arra gondolunk, hogy az angol „percolation” szó hétköznapi jelentése „szivárgás”, ez összhangban is van a fenti folyadékterjedést használó képpel.

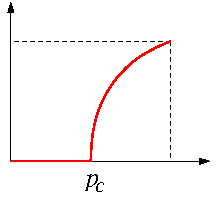
A perkoláció eseményének valószínűségét $\theta(p)$ -vel jelöljük. Ami igazán érdekes, az nem egy-egy $\theta(p)$ érték valamilyen konkrét $p$ -re, hanem magának a $p\mapsto \theta(p)$ függvénynek a viselkedése. Az világos, hogy $\theta(0)=0$ és $\theta(1)=1$ , hiszen a $p=0$ esetben egyáltalán nincsenek nyílt élek, míg a $p=1$ esetben minden él nyílt. Szemléletesen az is nyilvánvaló, hogy $\theta(p)$ a $p$ -nek növekvő (bár nem szigorúan növekvő) függvénye. Aki először találkozik a témával, esetleg azt is meggyőzőnek érezte volna, ha az előbb „szigorúan növekvőt” mondtunk volna. Ez azonban nincs így: ha $p$ elég kicsi pozitív szám, akkor $\theta(p)=0$ és azon $p$ -k szuprémuma, amikre $\theta(p)=0$ , a modell legizgalmasabb paramétere, az úgynevezett kritikus valószínűség: $p_c:=\sup\big\{p\in [0,1]:\theta(p)=0\big\}$ .

2. ábra.

Nem nehéz igazolni, hogy tetszőleges végtelen összefüggő gráfban, ha egy fix $o$ csúcs fürtje nulla valószínűséggel végtelen, akkor majdnem biztosan minden fürt véges. Másrészt, ha $o$ fürtje pozitív valószínűséggel végtelen, akkor majdnem biztosan lesz valahol a gráfban egy végtelen fürt. (Ez a Kolmogorov 0-1 törvényből következik, miután észrevettük, hogy egy végtelen fürt létezése farokesemény: bekövetkezése független bármely véges sok él állapotától). Tehát, ha $0<p_c<1$ , akkor a $p \in [0,p_c)$ szubkritikus és a $p \in (p_c,1]$ szuperkritikus intervallumban teljesen máshogy viselkedik a rendszer – erre mondjuk, hogy fázisátmenet történik $p_c$ -ben, és a $p_c$ környékén tapasztalható kritikus jelenségekre vagyunk a legkiváncsibbak.

Ez emlékeztetheti az Olvasót olyan valós fázisátmenetekre, mint hogy a víz megfagy, vagy a vas mágnesezhetővé válik egy bizonyos kritikus hőmérséklet alatt, vagy arra, hogy ha egy vírus reprodukciós rátája $1$ fölé kerül, akkor a populáció egy óriási részét megfertőzi. A közös jelenség, hogy ha a lokális interakciók elég erősek (pl. a molekulák egymást vonzó hatása legyőzi a hőből származó rezgéseket, vagy elég nagy valószínűséggel fertőzöm meg az ismerőseimet), akkor globális rend alakul ki a rendszerben. Egy végtelen fürt megjelenése a globális rend eléggé naiv analógiájának tűnhet, ám kiderült, hogy az analógia rendkívül erős (pl. a mágnesesség Ising modelljének Fortuin-Kasteleyn-féle „véletlen fürt” reprezentációján keresztül), és így a perkoláció tanulságai a teljes statisztikus fizika számára relevánsak.

Egy tetszőleges végtelen gráfon nem mindig igaz, hogy a $p_c$ szigorúan 0 és $1$ közé esik, és ha $\mathbb{Z}^2$ helyett az egydimenziós $\mathbb{Z}$ -n vizsgáljuk a fenti folyamatot, akkor könnyű látni, hogy ott a kritikus valószínűség $1$ . Ajánljuk az Olvasónak, hogy ha új neki ez a fogalom, akkor gondolja át, hogy ez miért igaz $\mathbb{Z}$ -re, illetve annak bármilyen „véges kiterjesztésére”, mint például a $\mathbb{Z}\times [0,k]$ „sávra”.

A négyzetrácsra valóban teljesül $0<p_c<1$ , és ezt még Broadbent és Hammersley bizonyították be. A könnyebb irány, hogy ha egy gráfban minden fokszám legfeljebb $D$ , akkor $1/(D-1) \leq p_c$ . Ez azért van, mert annak a valószínűsége, hogy van végtelen nyílt út egy $o$ csúcsból, legfeljebb $D(D-1)^{n-1} p^{n}$ minden $n$ -re, ami 0-hoz tart, ha $p<1/(D-1)$ . A formula onnan jön, hogy ha van végtelen nyílt út, akkor van $n$ hosszú önnemmetsző nyílt út is $o$ -ból, melyeknek a száma az eredeti gráfban legfeljebb $D(D-1)^{n-1}$ , és mindegyik út $p^n$ valószínűséggel nyílt. Speciálisan, $1/3 \leq p_c(\mathbb{Z}^2)$ .

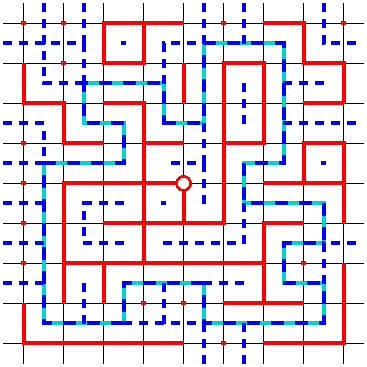
3.ábra

Az érdekesebb egyenlőtlenség a $p_c<1$ , amiről már láttuk az egydimenziós $\mathbb{Z}$ és hozzá hasonló gráfok példáján, hogy nem is teljesül mindig. A $\mathbb{Z}^2$ rácson egy fontos trükk a duális rács és azon egy duális perkoláció bevezetése: ha adott egy perkolációs konfiguráció a rácson (a 3. ábrán pirossal a nyílt élek), a duális konfigurációban egy duális él pontosan akkor duális-nyílt (kék szaggatott az ábrán), ha az őt metsző eredeti él zárt volt. Szemléletesen világos (bizonyítani kicsit fáradságos), hogy az eredeti $\mathbb{Z}^2$ konfigurációban az $o$ fürtje pontosan akkor véges, ha a duális konfigurációban van egy duális-nyílt kontúr, ami körbeveszi $o$ -t, és így elzárja őt a végtelentől (türkizzel az ábrán). És így már a kezünkben van a Peierls kontúr-módszer, hogy $p_c(\mathbb{Z}^2)$ -re fölső becslést adjunk, nagyon hasonlóan az alsó becsléshez: nem nehéz látni, hogy az $o$ -t körbevevő $n$ hosszú duális kontúrok száma legfeljebb $n3^n$ ; annak a valószínűsége, hogy egy ilyen kontúr duális-nyílt, az $(1-p)^n$ ; így annak a valószínűsége, hogy van $N$ -nél hosszabb duális-nyílt kontúr, az legfeljebb $\sum_{n \geq N} n3^n(1-p)^n$ , ami kisebb, mint $1$ , ha $p>2/3$ és $N$ elég nagy. Ebből következik, hogy valahol a $\mathbb{Z}^2$ -ben pozitív valószínűséggel lesz végtelen fürt, tehát $p_c(\mathbb{Z}^2)\leq 2/3$ .

Ha $d\ge 3$ , akkor a $\mathbb{Z}^d$ kockarács tartalmazza a $\mathbb{Z}^2$ rácsot, így $1/(2d-1) \leq p_c(\mathbb{Z}^d) \leq 2/3$ is világos, azaz nemtriviális fázisátmenet van. Azonban Benjamini és Schramm 1996-ban kezdeményezték, hogy a perkolációt nem csak a klasszikus statisztikus fizika $\mathbb{Z}^d$ rácsain kellene vizsgálni, hanem általános gráfokon is, különösképpen tranzitívakon (ami azt jelenti, hogy a gráf bármely két csúcsához létezik olyan gráf-automorfizmus, amely az egyik csúcsot a másikba viszi: a gráf ugyanúgy néz ki minden pontjából, homogén). A korlátos fokú végtelen tranzitív gráfok legfőbb forrása pedig a végesen generált végtelen csoportok Cayley-gráfjai: ha $\Gamma$ egy csoport, egy szimmetrikus véges $S=S^{-1}$ generátor-rendszerrel, akkor a $\mathsf{Cay}(\Gamma, S)$ gráf csúcsai a csoport elemei, élei pedig a $(\gamma,\gamma s)$ párok, ahol $\gamma\in \Gamma$ és $s\in S$ . Mivel szimmetrikus generátorrendszert választottunk, ez a gráf valójában irányítatlan: ha $(\gamma,\gamma s)$ egy él, akkor $(\gamma s,\gamma s s^{-1})=(\gamma s,\gamma)$ is az. A geometriai csoportelmélet alapvetése, hogy a Cayley-gráfok nagyléptékű geometriai tulajdonságai (azaz amiket a gráfra „messziről, hunyorítva ránézve” láthatunk) sok csoportelméleti tulajdonságot tükröznek (speciálisan, a konkrét generátor-rendszer sem fog számítani). A nagyléptékű geometriai tulajdonságoktól pedig azt várjuk, alapvetően befolyásolják a gráfon való perkoláció viselkedését.

Először is: igaz-e, hogy csak az „1-dimenziós” gráfokra lesz a fázisátmenet triviális, $p_c=1$ ? Ehhez természetesen definiálnunk kellene egy gráf dimenzióját. Valószínűségszámítási szempontból a leghasznosabbnak az izoperimetrikus egyenlőtlenségek fogalma bizonyult. Azt mondjuk, egy korlátos fokú gráf izoperimetrikus dimenziója legalább $d$ , ha minden $S$ véges csúcshalmazra $\vert\partial_E S\vert > c$ , $\vert S\vert^{(d-1)/d}$ teljesül valamilyen abszolút $c>0$ konstanssal, ahol a $\partial_E S$ élhatár azon élek halmaza, amiknek egyik végpontja $S$ -ben, a másik $S$ -en kívül van. Például $\mathbb{Z}$ -ben csak annyit tudunk mondani, hogy egy véges csúcshalmaz határa legalább kettő (akármekkora halmazról van is szó), így az izoperimetrikus dimenzió 1. Sokkal kevésbé triviális, de igaz, hogy $\mathbb{Z}^d$ izoperimetrikus dimenziója $d$ ; sőt, sokkal általánosabban, ha egy tranzitív gráf nem a $\mathbb{Z}$ egy véges kiterjesztése, akkor izoperimetrikus dimenziója legalább $2$ (tehát nem lehet például $1.17$ ). A 3-reguláris $\mathbb{T}_3$ fára pedig akármilyen véges $S$ csúcshalmazra egy lineáris izoperimetrikus egyenlőtlenség, $\vert\partial_E S \vert\geq \frac{3}{ 2} \vert S\vert$ teljesül, azaz az izoperimetrikus dimenzió végtelen.

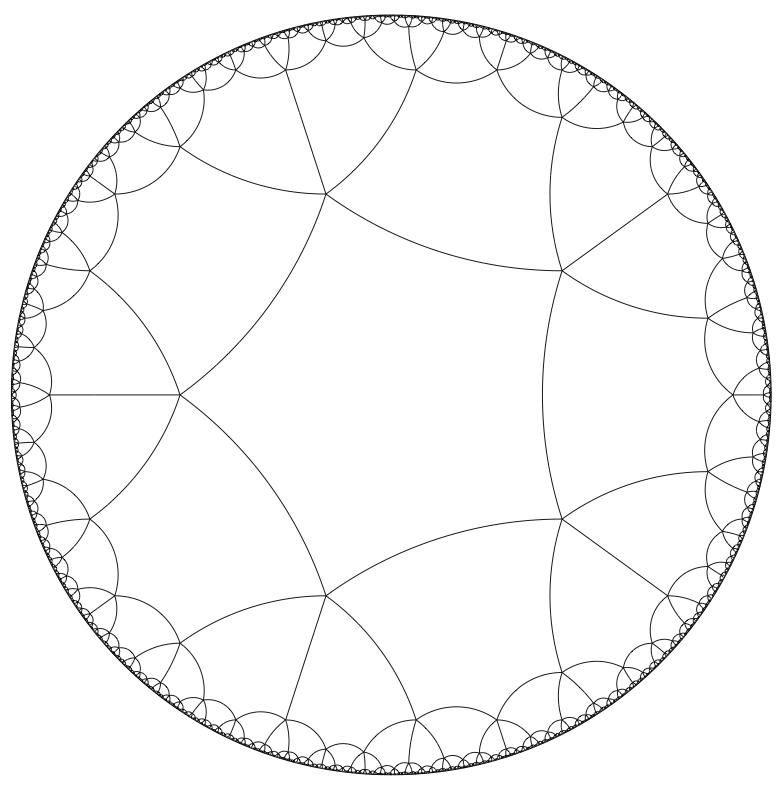
4.ábra

Az utolsó eset különösen fontos: azt mondjuk, egy korlátos fokú gráf amenábilis, ha nem teljesül a lineáris izoperimetrikus egyenlőtlenség, azaz ha létezik benne véges $F_n$ csúcshalmazoknak olyan sorozata, amelyre ${\vert\partial_E F_n\vert} / {\vert F_n\vert} \to 0$ . Például a $\mathbb{Z}^d$ rácsok, vagy minden szubexponenciális térfogat-növekedésű gráf amenábilis, míg a reguláris fák vagy a hiperbolikus terek csempézései (4. ábra) nem. A fogalom jelentőségét az adja, hogy Følner 1955-ben bizonyította, hogy egy csoport tetszőleges Cayley-gráfja pontosan akkor amenábilis, ha a csoport amenábilis abban az értelemben, ahogyan Neumann János 1929-ben definiálta: van rajta eltolásinvariáns átlagolás. (Az elnevezés is innen ered: az „amenable” azt jelenti, „kezelhető”, ám Neumann egy szóviccet rejtett itt el: „a-mean-able”, azaz „átlagolható”.) Az amenábilis/nem-amenábilis dichotómia a legfontosabb megkülönböztetések közé tartozik a modern matematika számos területén.

Visszatérve a perkolációhoz, Benjamini és Schramm azt sejtették, hogy ha egy gráf izoperimetrikus dimenziója szigorúan nagyobb 1-nél, akkor $p_c<1$ , és igazolták is ezt nem-amenábilis gráfokra. Babson és Benjamini 1999-ben egy bonyolult algebrai topológiai érveléssel, majd Timár Ádám 2007-ben pár sorban, lineáris algebrával bizonyította, hogy ha egy csoport végesen prezentált (azaz véges sok relációval definiálható), akkor tetszőleges Cayley-gráfjában egy csúcsot a végtelentől elvágó élhalmazokban csak korlátos nagy lyukak lehetnek, amiből következik, hogy a Peierls kontúr-módszer egy általánosítása működik, és így $p_c<1$ . Pár éve igazolta Duminil-Copin, Goswami, Raoufi, Severo és Yadin, a Szabad Gauss Mező nevű véletlen magasságfüggvény segítségével, hogy ha egy korlátos fokú gráf izoperimetrikus dimenziója nagyobb 4-nél, akkor $p_c<1$ . Ezen eredmények együttesen lefedik az összes tranzitív gráfot, de tökéletesen nyitott például az 1 és 2 közötti izoperimetrikus dimenzió esete, amikor a bolyongás rekurrens, így a Szabad Gauss Mezőt nem is lehet definiálni.

Az izoperimetrikus egyenlőtlenségeknek alapvető hatása van a végtelen fürtök számára is. Az minden tranzitív gráfban igaz, hogy a végtelen fürtök száma vagy 0, vagy 1, vagy $\infty$ ; ugyanis, ha lehetne például 19, akkor a konfiguráció egy lokális módosításával, tehát még mindig pozitív valószínűséggel, ezekből kettőt össze lehetne ragasztani, így pozitív valószínűséggel 18 végtelen fürt lenne; ám ilyen kevert helyzetet, hogy a végtelen fürtök száma néha ennyi, néha annyi, a perkoláció úgynevezett ergodikussága nem enged meg. Arra, hogy végtelen sok végtelen fürt előfordulhat, egy triviális példa a $3$ -reguláris fa, minden $p \in (p_c,1)$ -re. (Újabb gyakorlat az Olvasónak). Azonban az derül ki, hogy amenábilis tranzitív gráfokban soha nem lehet végtelen sok végtelen fürt: intuitíven, ezek nem férnének el egymás mellett összeragadás nélkül. Ezt a homályos intuíciót Burton és Keane 1989-ben formálta elegáns bizonyítássá. Az állítás megfordítása Benjamini és Schramm (1996) egy másik híres sejtése: ha egy tranzitív gráf nem-amenábilis, akkor létezik olyan $p$ érték, ahol végtelen sok végtelen fürt van. Az ismert, hogy minden nem-amenábilis csoportnak van olyan Cayley-gráfja, ahol ez bekövetkezik, illetve minden úgynevezett Gromov-hiperbolikus tranzitív gráf is ilyen.

Rátérve a kritikus viselkedés tárgyalására, egy beavatatlan Olvasó úgy gondolhatja, a $p_c$ értéke a legfontosabb, amit a perkolációról egy gráfon tudhatunk; de ez nem egészen van így. Ami igaz, hogy néhány esetben a $p_c$ meghatározása az elmélet legfontosabb tételei között van. A $\mathbb{Z}^2$ rácson élperkolációra Harris 1960-ban igazolta, hogy $p=1/2$ -en nincs még perkoláció, majd Kesten 1980-ban, hogy minden $p>1/2$ értéken már van, tehát $p_c(\mathbb{Z}^2,$ él $)=1/2$ . Itt az $1/2$ -es értéket a rács öndualitásából, amit már az $1/3\leq p_c(\mathbb{Z}^2,$ él $) \leq 2/3$ bizonyításban láttunk, viszonylag könnyű megjósolni, ám a bizonyítás már jóval nehezebb. Hasonlóképpen, $p_c(\Delta,$ csúcs $)=1/2$ , ahol $\Delta$ a standard 6-reguláris háromszögrács. A $\mathbb{T}_d$ fára $p_c(\mathbb{T}_d,$ él $)=p_c(\mathbb{T}_d,$ csúcs $)=1/(d-1)$ , ugyanis itt nem nehéz bizonyítani, hogy az alsó becslés, amit láttunk, éles. Ez egy speciális esete annak, hogy egy elágazó folyamat majdnem biztosan kihal, ha a várható gyerekszám 1-nél kisebb, és pozitív valószínűséggel túlél, ha az 1-nél nagyobb. Viszont a legtöbb gráfra a $p_c$ pontos értékét nem ismerjük, és valószínűleg nem is fogjuk soha. Schramm lokalitás sejtése, hogy $p_c$ értéke egy tranzitív gráfban csak a gráf lokális struktúrájától függ: ha két tranzitív gráf, melyekre $p_c<1$ , egy nagy sugarú gömbben megegyeznek, akkor a $p_c$ értékeik közel vannak egymáshoz.

A $p_c$ definíciója önmagában semmit nem mond arról, hogy pont $p_c$ -nél van-e perkoláció vagy nincs. Talán meglepő, hogy $p_c$ értékének ismerete nélkül is tudjuk sok gráfról, hogy $\theta(p_c)=0$ , azaz még nincsen végtelen fürt; az a sejtés, hogy ez minden tranzitív gráfban teljesül, ahol $p_c<1$ . A fő motivációs példák a síkrácsok és a fák: előbbiben segít a síkdualitás, utóbbiban pedig 150 éve ismert, hogy a kritikus elágazó folyamatok még éppen kihalnak. A $\mathbb{Z}^d$ rácson, ha $d$ nagy, egy kritikus fürt olyan sokfelé nőhet, hogy a rövid körök hatása elenyészik, és a fán való perkoláció egy kis perturbációjának fogható föl a modell. Ezt a homályos reményt Hara és Slade 1990-ben az úgynevezett csipke sorfejtéssel formalizálni tudta $d\ge 19$ -re, amit pár éve Fitzner és van der Hosftad, hatékonyabbá téve a módszert, lehozott $d\ge 11$ -re. A sejtés bizonyítása a $\mathbb{Z}^3$ esetre a témakör Szent Gráljának számít. A nem-amenábilis Cayley-gráfokon való perkoláció tanulmányozását is részben ez a kérdés motiválta: a nem-amenabilitás lehetővé teszi fa-szerű struktúrák fölfedezését a gráfban, ami aztán elvezet a $\theta(p_c)=0$ bizonyításához, ahogy azt Benjamini, Lyons, Peres és Schramm megtette 1999-ben. Ezután pedig reménykedni lehet, hogy a hiperbolikus térben egyre sűrűbb csúcshalmazokon definiált gráfokra alkalmazva ezt, a hiperbolikus tér lokálisan euklidészi volta elvezethet egy bizonyításhoz az euklidészi térben is. Ezt a tervezett stratégiát egyelőre senkinek sem sikerült valóra váltania.

5. ábra

Az univerzalitás sejtés azt mondja, hogy a rendszer viselkedése a kritikus ponton, ellentétben magával a $p_c$ értékével, a lokális struktúrától egyáltalán nem, csak a nagyléptékű geometriától függ. Hogyan kell ezt elképzelni? A valószínűségszámítás legalapvetőbb univerzális jelenségét mindenki ismeri, aki egyetemen akár csak egy év matematikát is tanult, például szociológusként: a centrális határeloszlás-tétel szerint független azonos eloszlású változók összege közelítőleg normális eloszlású. Ez akkor is igaz, ha független véletlen vektorokat adunk össze; így például, ha egy tetszőleges síkrácson bolyongunk, azaz minden lépésben a lehetséges szomszédok egyikére ugrunk, mindegyikre ugyanakkora valószínűséggel, korábbi döntéseinktől függetlenül, akkor sok lépés után a helyzetünk eloszlása közelítőleg normális lesz, elfeledve a síkrács diszkrét kombinatorikus részleteit. (Az 5. ábrán az egyszerű szimmetrikus bolyongás eloszlása látható 100 lépés után.)

6. ábra (Készítette Nagy Marcell)

Sőt, ha a teljes trajektóriát nézzük $n$ lépésig, akkor az ugrások nagyságát $\sqrt{n}$ -nel osztva létezik egy skálalimesz: a folytonos síkbeli Brown-mozgás. Ennek a limesznek pedig analitikusan kezelhető tulajdonságai, új szimmetriái vannak, amelyek rendkívül hasznossá teszik. A Brown-mozgásra Lévy 1940-ben bizonyította, hogy konforminvariáns: ha egy olyan komplex analitikus függvényt alkalmazunk rá, amelynek a deriváltja sehol nem nulla (így lokálisan mindenütt egy nemdegenerált nyújtás és forgatás), akkor a trajektória képének eloszlása meg fog egyezni az eredeti eloszlással.

A perkoláción nem látszik, hogy bármi köze lenne a bolyongáshoz vagy a normális eloszláshoz. Mégis, a fizikusok általános elképzelése, hogy a kritikus ponton a perkoláció és a hozzá hasonló statisztikus fizikai modellek is teljesítik az univerzalitás sejtést, egy konforminvariáns skálalimesszel. Az univerzalitás bizonyítására és a skálalimesz tulajdonságainak megértésére kidolgozták a renormalizációs csoport módszert, és konform-téreleméleti eszközökel nagyon részletes állításokat tettek, hogyan is viselkedik a rendszer a kritikus pont közelében. A bökkenő csak az, hogy ezek a technikák, bár matematikai formulákat és gondolatokat tartalmaznak, egyáltalán nincsenek szigorúan megalapozva, így a matematikusok számára ezek csak előrejelzésekként jelennek meg, amelyek jogosságára a legfőbb bizonyítékot számítógépes szimulációk jelentik.

Mit értünk részletes előrejelzések alatt? Például annak a valószínűsége, hogy az $o$ csúcs fürtje legalább $R$ távolságra elér $o$ -tól, szubkritikus perkolációban exponenciális gyorsan cseng le $R$ -ben; szuperkritikus perkolációban $R$ -től függetlenül $\theta(p)>0$ fölött marad; kritikus perkolációban pedig polinomiálisan cseng le, $R^{-1/\rho+o(1)}$ alakú, ahol a furcsa $1/\rho$ jelölésnek fizikatörténeti okai vannak. Ez az $1/\rho$ kitevő egy tipikus kritikus exponens, aminek értéke minden síkrácson $5/48$ kellene, hogy legyen, reguláris fákon és minden nem-amenábilis Cayley-gráfon $1$ , és a $\mathbb{Z}^d$ rácsokon, minden $d>6$ esetén, szintén 1. Egy közelkritikus exponens pedig $\theta(p_c+\epsilon)=\epsilon^{\beta+o(1)}$ , ami persze magában foglalja azt az előrejelzést is, hogy $\theta(p_c)=0$ . Síkrácsokon $\beta=5/36$ , reguláris fákon és a többi „nagy” gráfon $\beta=1$ . Mindebből remélhetőleg megérti az Olvasó a fizikusok kritikus exponensek iránti lelkesedését: ha ennyire univerzális számokat kapunk, a rácsok lokális részleteitől függetlenül, akkor valódi fizikai jelenségekkel kell, hogy szemben álljunk.

Ezekből a grandiózus sejtésekből mi az, amire szigorú matematikai bizonyítás van? Reguláris fákra expliciten számolni lehet a kérdéses valószínűségeket, így minden exponens ismert. A $\mathbb{Z}^d$ , $d\ge 11$ , rácsokon a fentebb említett csipke-sorfejtés a kritikus exponenseket is igazolja. Sőt, a módszer működik minden $d>6$ -ra, ha a $\mathbb{Z}^d$ -t módosítjuk úgy, hogy extra éleket adunk hozzá, minden olyan csúcsot is összekötve, amiknek a távolsága valamilyen alkalmas $L(d)$ -n belül van. Hogy miért pont $d=6$ körül kezd el úgy viselkedni a $\mathbb{Z}^d$ rács a perkoláció szempontjából, mintha nem lenne nemtriviális geometriája, annak okait most nincs módunk leírni, de mindenesetre a $d=3,4,5$ dimenziók kritikus exponensei mind mások, és pontos értékükről a fizikusoknak sincs elképzelése. A reguláris fákhoz és magas dimenziókhoz tartozó úgynevezett átlag-tér (geometria nélküli) exponenseket „nagyon”-nem-amenábilis és hiperbolikus tranzitív gráfokra is igazolták már, de az általános nem-amenábilis eset nyitott.

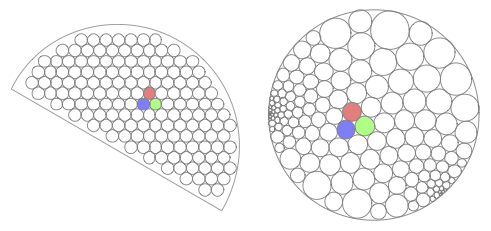
7. ábra. (Készítette: Oded Schramm, Wikipedia)

A másik véglet a kétdimenziós eset. Amögött, hogy itt nagyon sok mindent értünk, egy speciális tulajdonsága van a két dimenziónak. Ez pedig az, hogy a konform leképezések rendkívül gazdagok ebben a dimenzióban, amit a Riemann leképezési tétel is mutat: bármely két egyszeresen összefüggő tartomány, ami nem maga az egész sík, átvihető egymásba konform leképezéssel (a 7. ábrán egy ilyen leképezésnek egy körpakolásos közelítését láthatjuk). Ez pedig azt jelenti, hogy ha tudjuk (vagy legalábbis föltesszük) a modell konform-invarianciáját, akkor nagyon sok eszközünk lesz számításokhoz.

8. ábra. (Készítette: Oded Schramm)

Oded Schramm 2000-ben megkonstruálta síkbeli konforminvariáns véletlen görbék egy családját, amit Sztochasztikus Loewner Evolúciónak vagy Schramm-Loewner Evolúciónak is neveznek, de mindig SLE-nek rövidítenek. Ennek segítségével bármilyen, a komplex felső félsíkbeli, önelkerülő, konform-invariáns és a térbeli Markov-tulajdonsággal rendelkező véletlen görbét (mint amilyen a $\Delta$ háromszögrácson a zárt és nyílt csúcsok közötti határgörbe skálalimesze kell, hogy legyen, ha az létezik és konforminvariáns) elkódolt a félsík határán mozgó egydimenziós Brown-mozgássá. Egy szép költői képpel élve, mintha a Brown-mozgás egy kisgyerek lenne, aki egy papírsárkánnyal fut a szélben, egyre magasabbra engedve és közben ide-oda rángatva azt. A kisfiú mozgását a sárkány mozgásával a Loewner-egyenlet köti össze.

9. ábra. (Készítette: Oded Schramm)

Egy olyan kérdést, hogy egy nagy négyzet két szemközti oldala össze van-e kötve egy fürttel, meg lehet válaszolni úgy, hogy a négyzet egyik sarkából indított határgörbe a négyzet melyik szemközti oldalát találja el először. Vagy az, hogy egy fürt határának dimenziója $2-\delta$ , körülbelül azt jelenti, hogy a görbe $\epsilon^{\delta+o(1)}$ valószínűséggel halad el egy tipikus pont $\epsilon$ környezetében. Ezeket a kérdéseket pedig a Loewner-egyenlet lefordítja egy egydimenziós sztochasztikus differenciálegyenlet-kérdéssé, így számolhatóvá teszi. (A 9. ábrán a háromszögrácson egy csúcsperkolációs fürt látható feketével, az őt érintő további fürtök különböző színekkel. A határgörbe skálalimeszének dimenziója 7/4.) Ezzel az SLE lehetőséget teremtett a fizikusok által sejtett eredmények matematikai bizonyítására, teljesen más módszerekkel, ugyanis nem valószínűségek, függvények limeszéről beszél, hanem megkonstruál egy folytonos geometriai limesz-objektumot.

A sikerhez persze az is kell, hogy tudjuk a modell konforminvarianciáját. A háromszögrácson való csúcsperkoláció esetén erre Smirnov 2001-ben talált egy gyönyörű bizonyítást. Ez egy kombinatorikus varázslaton alapul, amelyet más síkrácsokra egyelőre nem sikerült átvinni, így a síkbeli kritikus perkoláció univerzalitása továbbra is nyitott.

Természetes kívánság, hogy ne csak egyetlen határgörbének legyen skálalimesze (egy SLE görbe), hanem az egész konfigurációnak. Fölmerülhet ötletként, hogy limeszként a sík minden pontját válasszuk egymástól függetlenül nyíltnak vagy zártnak. Mondjuk kontinuum sok pénzfeldobást kicsit nehéz kivitelezni, nem is egészen világos, hogy pontosan mit jelentene, de végülis a fehér zaj, amit a fizikusok gond nélkül használnak, a sztochasztikus differenciálegyenletek elméletében pedig a Brown-mozgás „deriváltjaként”, $\mathrm{d} B_t$ -ként a matematikusok is ismernek, lényegében pont ez. Csakhogy a fehér zaj tényleges matematikai értelmezése az integráljaival történik: azt méri, hogy egy intervallumon, vagy kétdimenziós perkoláció esetén egy korlátos síkdarabon az átlaghoz képest mennyivel több nyílt csúcs van. És a kritikus perkoláció leírására ez alkalmatlan. Ugyanis, talán megdöbbentő módon, a makroszkopikus fürtstruktúra, amiről a skálalimesz beszélni kívánna, független attól, hogy hol van az átlagnál több vagy kevesebb nyílt csúcs. Másképp mondva, a makroszkopikus fürtstruktúra rendkívül zajérzékeny: a csúcsok elenyésző részének véletlen újrasorsolása tipikusan nem változtatja meg lényegesen a nyílt csúcsok számát sehol, ám a fürtstruktúrát teljesen átrendezi. Így a fürtstruktúra skálalimeszének egy helyes és intuitív definíciója az összes fürt határgörbéiből történik, ami zárt folytonos síkgörbék megszámlálható uniója, így egy viszonylag épeszű topologikus tér, amin a kritikus perkoláció skálalimesze egy valószínűségi mérték. A nemrég elhunyt Boris Tsirelson zajelméletének elnevezése szerint pedig ez a skálalimesz a zajérzékenysége miatt egy fekete zaj.

A síkbeli kritikus perkoláció zajérzékenységének pontos mértékét a jelen írás második szerzője Garbannal és Schramm-mal együtt értette meg, aminek a következő csinos alkalmazása is van dinamikus perkolációra. A végtelen háromszögrácson minden csúcs kapcsolgasson folytonos idejű Poisson-órák szerint, egymástól függetlenül, ide-oda nyílt és zárt között szimmetrikusan. Így minden egyes fix pillanatban minden csúcs 1/2 valószínűséggel nyílt, 1/2-del zárt, tehát kritikus perkolációt látunk, és $\theta(1/2)=0$ miatt majdnem biztosan nincs végtelen fürt. Csakhogy most számít a nulla valószínűségű és a ténylegesen üres események közötti különbség: kontinuum sok időpont van, és a nulla valószínűséget nem tudjuk ennyiszer összeadni, tehát elvileg lehetséges, hogy vannak véletlen kivételes időpontok, amikor kialakul végtelen fürt. És ez valóban be is következik: az olyan kivételes időpontok halmaza, amikor az origó fürtje végtelen, egy $31/36$ -dimenziós véletlen Cantor-halmaz.

A $\mathbb{Z}^d$ rácsokon, ha $d\ge 6$ , akkor a perkolációs utak már nagyon hasonlítanak független elágazó bolyongás-trajektóriákra, így a skálalimesz $\mathbb{R}^d$ -ben az úgynevezett integrált szuper-Brown-mozgással írható le, bár ez az állítás nincs minden részletében bizonyítva. Hogy mi lenne a skálalimesz $3\leq d \leq 5$ esetén, és mi lenne egy tetszőleges tranzitív gráfnál, ahol nincs az $\mathbb{R}^d$ -hez hasonló természetes folytonos limesztér, azt a jelen pillanatban teljes homály fedi.

A perkolációs modelleknek rendkívül sok változata létezik, például folytonos alaptéren definiált gráfokra való áttéréssel, vagy a nyílt/zárt döntések függetlenségének a legkülönbözőbb módokon való föladásával. Az AMS MathSciNet adatbázisában a „percolation” kifejezés a jelen pillanatban 4273 cikkre illik.

Írásunknak a kezdőlökést Harry Kesten 2006-os Notices of the AMS-beli What is ... percolation? cikke adta. További olvasnivalónak pedig a kövezkezőket ajánljuk:

Irodalomjegyzék

[1] Hugo Duminil-Copin. Sixty years of percolation. Proceedings of the ICM 2018, Rio de Janeiro. http://arxiv.org/abs/1712.04651
: [2] Hugo Duminil-Copin, Subhajit Goswami, Aran Raoufi, Franco Severo, and Ariel Yadin. Existence of phase transition for percolation using the Gaussian Free Field. Duke Math. Journal, to appear. http://arxiv.org/abs/1806.07733
: [3] Hugo Duminil-Copin and Vincent Tassion. A new proof of the sharpness of the phase transition for Bernoulli percolation on 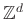$\mathbb{Z}^d$ . L'Enseignement Mathématique 62 (2016), 199–206. http://arxiv.org/abs/1502.03051; [4] Christophe Garban and Jeff Steif. Noise sensitivity of Boolean functions and percolation. Cambridge University Press, 2014. http://math.univ-lyon1.fr/~garban/Fichiers/book.pdf; [5] Geoffrey Grimmett. Percolation. Second edition. Grundlehren der Mathematischen Wissenschaften, 321. Springer-Verlag, Berlin, 1999.; [6] Tom Hutchcroft. Percolation on hyperbolic graphs. Geometric and Functional Analysis 29 (2019), 766–810. http://arxiv.org/abs/1804.10191; [7] Russell Lyons and Yuval Peres. Probability on trees and networks. Cambridge University Press, 2016. Available at http://mypage.iu.edu/~rdlyons; [8] Gábor Pete. Probability and Geometry on Groups. Book in preparation, http://www.math.bme.hu/~gabor/PGG.pdf; [9] Gordon Slade. Scaling limits and Super-Brownian Motion. Notices of the AMS 49 (2002), 1056–1067. https://www.ams.org/journals/notices/200209/fea-sladecolor.pdf
: [10] Wendelin Werner. Lectures on two-dimensional critical percolation, IAS Park City Graduate Summer School, 2007. http://arxiv.org/abs/0710.0856