Mi is ... egy elliptikus génusz?

Az elliptikus génusz a génusz fogalmának egy speciális típusa, amelyet kvantumtérelméleti kérdések vizsgálatához fejlesztettek ki. Tárgyalásunkat a génusz általános fogalmával kezdjük, majd átvesszük Hirzebruch multiplikatív génuszokra vonatkozó elméletét, amelybe az elliptikus génusz fogalma nagyon szépen beilleszthető.

Génuszok. Egy multiplikatív génusz, vagy egyszerűen csak génusz egy olyan szabály, amely minden zárt, irányított sima $M^n$ sokasághoz egy $\Lambda$ ${\mathbb{Q}}$ -algebra egy $\varphi (M^n)$ elemét rendeli úgy, hogy kielégíti a következő feltételeket:

(1) $\varphi (M^n \sqcup N^n)=\varphi (M^n)+\varphi (N^n)$ ; itt $M^n \sqcup N^n$ a két $n$ -dimenziós sokaság diszjunkt unióját jelöli.

(2) $\varphi (M^n \times V^m)=\varphi (M^n)\cdot \varphi (V^m)$ .

(3) $\varphi (M^n)=0$ ha $M^n=\partial W^{n+1}$ a $W^{n+1}$ kompakt $(n+1)$ -sokaság irányított határa.

Az (1)-es és (3)-as tulajdonságokból azonnal következik, hogy ha $M^n$ és $N^n$ kobordáns sokaságok, vagyis létezik egy olyan $W^{n+1}$ kompakt, irányított sokaság, amely határa éppen $M^n\sqcup (-N^n)$ (ahol $-N^n$ as $N^n$ sokaságot jelöli irányítása megfordítása után), akkor $\varphi (M^n)=\varphi (N^n)$ . Másként fogalmazva, a $\varphi (M^n)$ érték csak az $M^n$ sokaságnak az $\Omega _*^{SO}$ kobordizmus-csoportban reprezentált $[M^n]$ osztályától függ, így $\varphi$ -re tekinthetünk úgy is mint egy

$\displaystyle \varphi \colon \Omega _* ^{SO}\to \Lambda$

gyűrű-homomorfizmusra.

Az $\Omega _*^{SO}$ gyűrű struktúrája meglehetősen bonyolult. Ezzel szemben $\Omega _* ^{SO} \otimes {\mathbb{Q}}$ a ${\mathbb{C}}P^{2k}$ komplex projektív terek kobordizmus-osztályai által generált ${\mathbb{Q}}[[{\mathbb{C}}P^2], [{\mathbb{C}}P^4], [{\mathbb{C}}P^6], \ldots ]$ polinomgyűrűvel egyenlő. Ebből rögtön következik, hogy a génusz eltűnik azokon a sokaságokon, amelyek dimenziója nem osztható 4-gyel, és a génuszt teljesen meghatározza az, hogy milyen értékeket vesz fel a ${\mathbb{C}}P^{2k}$ sokaságokon. A

$\displaystyle g(u)=u+\frac{\varphi ( {\mathbb{C}}P^2)}{3}u^3+\frac{\varphi ( {\mathbb{C}}P^4)}{5}u^5+\cdots \in \Lambda [[u]]$

hatványsort $\varphi$ logaritmusának nevezik. Erre teljesülnek a

$\displaystyle g(-u)=-g(u), \qquad g(u)=u +{\mathfrak{o}}(u)$

azonosságok, valamint a hatványsor meghatározza $\varphi$ -t. Fordítva, minden ilyen hatványsor egy multiplikatív génusz logaritmusa.

Egy zárt, irányított $n=4m$ -dimenziós $M^n$ sokaság $\sigma (M^n)$ szignatúrája talán a legismertebb példa a génusz fogalmára. A szignatúrát a $H^*_{DR}(M^n)$ de Rham kohomológia segítségével a következő módon lehet definiálni: $\alpha$ és $\beta$ $M^n$ -en lévő zárt $2m$ -formákra a

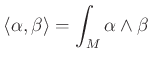
$\displaystyle \langle \alpha, \beta \rangle = \int _M \alpha \wedge \beta$

formula egy nemelfajuló szimmetrikus bilineáris formát ad a $H^{2m}_{DR}(M^n)$ véges dimenziós vektortéren. Az $M^{4m}$ sokaság szignatúrája definíció szerint e forma indexe. A Poincaré dualitás egy következményeként belátható, hogy $\sigma$ egy kobordizmus-invariáns. Logaritmusát pedig a

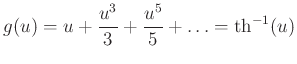
$\displaystyle g(u)=u+\frac{u^3}{3}+\frac{u^5}{5}+\ldots =\operatorname{th}^{-1}(u)$

függvény adja.

Egy másik, hasonlóan fontos példa génuszra az ${\widehat{A}}$ -génusz, amelynek logaritmusa a $g(u)=2\operatorname{sh}^{-1}(u/2)$ függvény. Ezen ${\widehat{A}}$ -génusz az algebrai geometriából ismert aritmetikai génuszhoz is kapcsolódik.

Friedrich Hirzebruch a Svájci Matematikai Társulat (SMS) 2010. évi centenáriumi konferenciáján (https://math.ch/about-sms/centennial/)

Hirzebruch formalizmusa. Az 1950-es évek kezdetén F. Hirzebruch a multiplikatív génuszok egy csodálatos, a Pontrjagin-számokra alapozott leírását találta meg. Egy $M^n$ Riemann-sokaságra a $p_i\in H^{4i}_{DR}(M^n)$ Pontrjagin-osztályt egy, a görbületi tenzorból származtatható $\rho _i$ zárt $4i$ -forma reprezentálja. Amennyiben $n=4m$ és $\omega =(i_1, i_2, \ldots , i_s)$ az $m$ egy partíciója, akkor a $p_{\omega}[M^n]$ Pontrjagin-számot a

$\displaystyle p_{\omega}[M^n]=\int _M \rho _{i_1}\wedge \rho _{i_2}\wedge \ldots \wedge\rho _{i_s}$

integrál definiálja. R. Thom alapvető munkája szerint minden $\Omega _n ^{SO}\to \Lambda$ homomorfizmus a Pontrjagin-számok ( $\Lambda$ feletti) lineáris kombinációjaként állítható elő. Ez az elv természetesen a multiplikatív génuszokra is vonatkozik. Legyen tehát $\varphi$ egy $g(u)$ logaritmusú génusz, és legyen $s(u)\in \Lambda [[u]]$ a $g(u)$ formális inverze, vagyis az a formális hatványsor, amelyre $g(s(u))=u$ teljesül. Ennek a hatványsornak $g$ -hez hasonló tulajdonságai vannak: $s(-u)=-s(u)$ , $s(u)=u+{\mathfrak{o}}(u)$ . Vegyük a

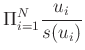
$\displaystyle \Pi _{i=1}^N \frac{u_i}{s(u_i)}$

szorzatot, ahol $u_1, u_2, \ldots , u_N$ 2 súlyú formális változók (és $N$ nagy). Mivel ez egy $u_i$ -kben szimmetrikus kifejezés, valamint minden változóban páros, ezért felírható az $u_1^2, u_2^2, \ldots , u_N^2$ tagok elemi szimmetrikus polinomjaiban. Helyettesítsünk $p_i$ -t az $i$ -edik elemi szimmetrikus polinom helyére, és legyen $K_m(p_1, p_2, \ldots , p_m)$ az eredmény azon része, amely $H^{4m}_{DR}(M)$ -be esik. Hirzebruch tétele szerint ekkor

$\displaystyle \varphi (M^{4m})=K_m (p_1, , p_2, \ldots , p_m )[M^{4m}].$

Szigorú multiplikativitás. Mint minden génusz, a szignatúra is teljesíti a $\sigma (M^n\times N^k)=\sigma (M^n)\cdot \sigma (N^k)$ azonosságot. S. S. Chern, F. Hirzebruch és J.-P. Serre egy eredménye alapján azonban egy sokkal erősebb multiplikativitás is teljesül. Legyen $G$ egy kompakt, összefüggő Lie-csoport, és legyen $E$ egy $B$ zárt, irányított sokaság feletti principális $G$ -nyaláb. Tegyük fel továbbá, hogy $G$ -nek egy zárt, irányított $V$ sokaságon való sima hatása is rögzítve van. Ekkor megkonstruálható az $E\times _G V$ , $B$ feletti $V$ fibrumú asszociált nyaláb. Feltéve, hogy az $E\times _G V$ nyaláb irányítása kompatibilis $B$ és $V$ irányításával, azt kapjuk, hogy

$\displaystyle \sigma (E\times _GV)=\sigma (B)\cdot \sigma (V),$

amit általában a szignatúra szigorú multiplikativitásának nevezünk. Vegyünk például egy $\xi$ $k$ -dimenziós komplex nyalábot $B$ felett, és legyen ${\mathbb{C}}P(\xi )$ az ehhez asszociált projektív nyaláb. E nyaláb egy $b\in B$ pont feletti fibruma ${\mathbb{C}}P(\xi _b) \cong {\mathbb{C}}P^{k-1}$ sokasággal lesz egyenlő, a szigorú multiplikativitás szerint pedig azt kapjuk, hogy

$\displaystyle \sigma ({\mathbb{C}}P(\xi ))=\sigma (B)\cdot \sigma ({\mathbb{C}}P^{k-1}).$

Ebből következően, páros $k$ esetén $\sigma ({\mathbb{C}}P(\xi ))=0$ pusztán dimenzió okokból.

Elliptikus génuszok. Egy $\varphi$ multiplikatív génuszt elliptikus génusznak nevezünk, ha eltűnik minden olyan sokaságon, amely ${\mathbb{C}}P(\xi )$ alakban előáll valamely $B$ zárt, irányított sokaság feletti $\xi$ páros dimenziós komplex nyalábra. Az „elliptikus” jelző eredetét a következő, elliptikus integrált használó tétel magyarázza meg:

1. Tétel. A $\varphi$ génusz pontosan akkor elliptikus, ha $g(u)$ logaritmusára valamely $\delta, \epsilon\in \Lambda$ konstansok választásával teljesül, hogy

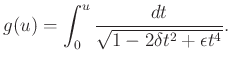
$\displaystyle g(u)=\int_0^u\frac{dt}{\sqrt{1-2\delta t^2+\epsilon t^4}}.$

A $\Lambda ={\mathbb{C}}$ és $\delta ^2\neq \epsilon \neq 0$ esetben (vagyis amikor a gyökjel alatti polinomnak négy különböző gyöke van) $g^{-1}(u)$ egy elliptikus függvény 0 körüli kifejtése. A $\delta ^2=\epsilon$ vagy $\epsilon =0$ esetekben az elliptikus génuszt elfajulónak nevezzük. Két fő példánk, a szignatúra és az $\widehat{A}$ -génusz a $\{\delta=\epsilon=1\}$ , illetve a $\{ \delta =-\frac{1}{8}, \epsilon=0\}$ eseteknek felelnek meg.

Páros $k$ esetén a ${\mathbb{C}}P^{k-1}$ projektív tér példa spin sokaságra. Egy $V^n$ sokaság spin, ha érintőnyalábjának struktúra csoportja a $\operatorname{Spin}(n)$ csoportra redukálható. (A Spin $(n)$ csoport az $SO(n)$ speciális ortogonális csoport nemtriviális kettős fedése.) Másképp fogalmazva, a $V^n$ sokaság spin, ha tetszőleges triangulációját véve érintőnyalábja trivializálható a 2-váz felett. A következő tétel R. Bott és C. Taubes merevségi tételével ekvivalens.

2. Tétel. Legyen $G$ egy kompakt összefüggő Lie-csoport, $E$ egy $B$ zárt, irányított sokaság feletti principális $G$ -nyaláb, $V$ pedig egy sima $G$ -hatással ellátott zárt spin sokaság. Ekkor minden $\varphi$ elliptikus génuszra

$\displaystyle \varphi (E\times _G V)=\varphi (B)\cdot \varphi (V).$

Modularitás. Legyen $\varphi$ a $\delta, \epsilon \in {\mathbb{C}}$ paraméterekhez tartozó ${\mathbb{C}}$ feletti nemelfajuló elliptikus génusz. Ismert, hogy az

$\displaystyle Y^2=X^4-2\delta X^2+\epsilon$

negyedrendű Jacobi-görbe a $H=\{ \tau \in {\mathbb{C}}\mid\operatorname{Im}(\tau)>0\}$ felső félsík pontjaival paraméterezhető. Evvel a paraméterezéssel $\delta$ és $\epsilon$ egy bizonyos $\Gamma _0(2)$ csoportra (amely $H$ Möbius-transzformációinak részcsoporja) nézve 2 súlyú moduláris formák lesznek. Mivel a $\varphi (M^{4m})$ értékek $\delta$ -ban és $\epsilon$ -ban polinomok, így maguk is moduláris formák, és $\varphi$ -re gondolhatunk mint egy, a $\Gamma _0(2)$ csoportra nézve moduláris formák $\Lambda = M_*(\Gamma _0(2))$ gyűrűje feletti elliptikus génuszra.

Hurokterek. E. Witten megfogalmazásában elliptikus génuszok megadhatók az ${\mathcal {L}}M$ szabad huroktéren értelmezett elliptikus operátorokkal, ahol ${\mathcal {L}}M$ az $S^1\to M$ szabad hurkok végtelen dimenziós sokasága. Az ilyen típusú operátorok fontos szerepet játszanak a kvantumtér-elméletekben. Ezen operátorok elmélete még nincs teljesen kidolgozva, de az index-tétel ilyen operátorokra sejtett kiterjesztései már most fontos dolgok megértéséhez vezettek. Az ${\mathcal {L}}M$ -en lévő Dirac operátor felcserélhető egy természetes $S^1$ -hatással, és indexe az $S^1$ -nek egy végtelen dimenziós reprezentációját adja. Witten megmutatta azt, hogy e reprezentáció karaktere természetesen azonosítható az $M$ sokaság $M_*(\Gamma_0(2))$ -értékű elliptikus génuszával.

További olvasmányok

Az elliptikus génusz fogalma először [1]-ben jelent meg. Az 1986-as Princeton-i konferencia kötete [3] többek között Witten azon cikkét is tartalmazza, amely az elliptikus génusz fizikai interpretációját adja meg. A merevségi tétel bizonyítása [4]-ben található. Végül pedig [2] a témakörbe nyújt elegáns és részletes bevezetést.

Felhasznált irodalom

[1] S. Ochanine, Sur les genres multiplicatifs définis par des intégrales elliptiques, Topology 26 (1987), 143–151.

[2] F. Hirzebruch, Th. Berger, és R. Jung, Manifolds and Modular Forms, Vieweg, 1992.

[3] Elliptic Curves and Modular Forms in Algebraic Topology, P. S. Landweber, editor, Lecture Notes in Mathematics 1326, Springer-Verlag, 1986.

[4] R. Bott és C. H. Taubes, On the rigidity theorems of Witten, J. Amer. Math. Soc. 2 (1989), 137–186.

Serge Ochanine

: Serge Ochanine a University of Kentucky professzora, e-mail címe: Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.. A cikk eredetileg az American Mathematical Society Notices folyóiratának 2009 június/júliusi számában jelent meg a What is ...? rovatban. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. A fordítást Stipsicz András készítette.; Serge Ochanine: WHAT IS...an Elliptic Genus? Notices Amer. Math. Soc. Vol.56 Num. 6. (June/July 2009) 720-721 ©2009 American Mathematical Society https://www.ams.org/notices/200906/rtx090600720p.pdf