Információk

Főmenü

 Aktuális szám: 12. szám 2019. június 

Douglas faktorizációs lemmája

Douglas faktorizációs lemmája

2018. február 27-én 80 éves korában elhunyt Ronald G. Douglas, az operátorelmélet egyik meghatározó alakja, számtalan nagy hatású könyv és cikk szerzője. Banach Algebra Techniques in Operator Theory [5] című munkája a téma klasszikusának számít.

Douglas legtöbbet idézett eredménye az általában csak Douglas faktorizációs lemmája néven emlegetett 1966-os tétele [4], mely a Google Scholar adatbázisa szerint 930 hivatkozással rendelkezik. Rövid írásunk célja, hogy e méltán híres eredményt körüljárjuk, és annak szépségét és hatékonyságát vázlatosan bemutassuk.

A lemmának magyar vonatkozása is van. Nevezetesen, Douglas a cikkében megemlíti, hogy a bizonyítás egyik nemtriviális gondolata Halmos Páltól számazik.

Halmos Pál 

1966-ban, amikor a faktorizíciós lemma született, mindketten a michigani egyetemen dolgoztak. Sőt, az alábbi képet maga Halmos készítette ugyanebben az évben.

Halmos Pál fotója Ronald G. Douglasről 

Mielőtt a tétel tárgyalását megkezdjük, vázlatosan összefoglaljuk a legalapvetőbb tudnivalókat.

A valós vagy komplex $ \mathcal{H}$ vektorteret euklideszi térnek nevezzük, ha a szokásos összeadás és számmal való szorzás műveletek mellett el van látva egy speciális kétváltozós

$\displaystyle \langle\cdot,\cdot\rangle\colon \mathcal{H}\times\mathcal{H}\to\mathbb{K} $

függvénnyel is, amit skalárszorzatnak hívunk. A skalárszorzat létének nagy előnye, hogy segítségével lehet hosszt, távolságot és szöget definiálni:

$ \Vert x\Vert=\sqrt{\langle x,x\rangle}$, $ d(x,y)=\Vert x-y\Vert$, $ \alpha=\arccos\frac{\langle x,y\rangle}{\Vert x\Vert\cdot\Vert y\Vert}$.

Példaként gondolhatunk itt az $ \mathbb{R}^2$ vektortérre a szokásos skalárszorzattal

$\displaystyle \langle(x_1,x_2),(y_1,y_2)\rangle:=x_1\cdot y_1+x_2\cdot y_2. $

Az ebből a skalárszorzatból nyert hossz-, távolság- és szögfogalom megegyezik a középiskolában tanultakkal. Az $ (x_1,x_2)$ vektor hossza épp $ \sqrt{x_1^2+x_2^2}$, két vektor „távolsága” épp a különbségvektor hossza, a szögre vonatkozó állítás pedig nem más, mint a koszinusz tétel egy átfogalmazása.

A hossz (és távolság) segítségével értelmezhetjük sorozatok konvergenciáját is, nevezetesen $ x_n\to x$, ha $ \Vert x_n-x\Vert\to 0$. Egy euklideszi teret Hilbert-térnek nevezünk, ha minden benne haladó Cauchy-sorozat konvergens. Más szóval, ha egy $ (x_n)$ sorozatra az teljesül, hogy $ \Vert x_n-x_m\Vert\to 0$ ( $ n,m\to\infty$), akkor van olyan $ x\in\mathcal{H}$, amelyre $ x_n\to x$. Megjegyezzük, hogy ez utóbbi úgynevezett teljességi feltevésnek köszönhető, hogy a Hilbert-terek geometriájának elmélete sokkal gazdagabb mint az euklideszi tereké.

A Hilbert-terek szerkezetének egyik legfontosabb (euklideszi terekre általában nem jellemző) tulajdonságára Riesz Frigyes híres eredménye világít rá: bármely lineáris $ M$ altér  $ \overline{M}$ lezártja és merőleges kiegészítője,

$\displaystyle M^{\perp}=\big\{x\in\mathcal{H}\mid\forall m\in M\colon \langle x,m\rangle=0\big\} $

direkt összegként feszíti ki a teret. Más szóval, minden $ \mathcal{H}$-beli elem egyféleképp írható fel egy $ \overline{M}$-beli és egy $ M^{\perp}$-beli elem összegeként.

Riesz Frigyes 

Megszokhattuk, hogy lineáris leképezések (vagy más szóval: lineáris operátorok) esetében bizonyos fogalmak leegyszerűsödnek, vagy éppen újabb tulajdonságokkal ruházódnak fel, így például egy lineáris leképezés nullhelyeinek halmaza (magtere) és értékkészlete (képtere)

$\displaystyle \ker A:=\{x\mid Ax=0\}\qquad\qquad\operatorname{ran}A:=\big\{Ax\mid x\in\mathcal{H}\big\} $

a $ \mathcal{H}$-nak egy-egy lineáris altere. Emlékeztetünk arra is, hogy a leképezés korlátossága egyenértékű a folytonosságával, amit viszont elég egyetlen pontban leellenőrizni.

Így tehát egy lineáris leképezés folytonos, ha van olyan $ K\geq0$ konstans, amellyel minden $ x\in\mathcal{H}$-ra fennáll az alábbi egyenlőtlenség

$\displaystyle \Vert Ax\Vert\leq K\cdot\Vert x\Vert. $

A legkisebb ilyen $ K$ számot az $ A$ leképezés operátornormájának nevezzük, és $ \Vert A\Vert _{\textrm{op}}$-pal jelöljük. Vegyük észre, hogy $ \Vert Ax\Vert\leq\Vert A\Vert _{\textrm{op}}\cdot\Vert x\Vert$ teljesül minden $ A$ folytonos lineáris operátorra és $ x\in\mathcal{H}$ elemre.

Riesz Frigyes egy másik alapvető fontosságú eredményének, az úgynevezett Riesz-féle reprezentációs tételnek egy elemi következménye, hogy minden folytonos lineáris leképezéshez természetes módon kapcsolódik egy úgynevezett adjungált operátor. Az $ A^*$ folytonos lineáris leképezést $ A$ adjungáltjának nevezzük, ha $ \langle Ax,y\rangle=\langle x,A^*y\rangle$ teljesül minden $ x,y$ vektorra. Az adjungálás defibíciójából az is látszik, hogy $ (AB)^*=B^*A^*$.

Megemlítjük még a zártgráf tételt, mint a Hilbert-terek operátorainak folytonosságára vonatkozó egyik alaptételt. A zártgráf tétel azt mondja ki, hogy egy $ A\colon \mathcal{H}\to\mathcal{H}$ lineáris leképezés pontosan akkor folytonos, ha a

$\displaystyle \operatorname{graf}(A)=\big\{(x,Ax)\mid x\in\mathcal{H}\big\}\subseteq\mathcal{H}\times\mathcal{H} $

halmaz zárt (a szorzattopológia szerint). Ez utóbbi pedig könnyedén ellenőrizhető sorozatok segítségével: Legyen $ (x_n)\subset \mathcal{H}$ egy olyan sorozat, amelyre $ x_n\to 0$ és $ Ax_n\to y$. Ekkor azt kell igazolnunk, hogy $ y=0$. Megjegyezzük, hogy a zártgráf tétel a Hilbert-tereknél általánosabb ún. Banach-terek körében is igaz, sőt a matematika számos egyéb területén is előfordul a zártgráf tétellel analóg állítás. (Ezzel kapcsolatban az olvasó figyelmébe ajánljuk Terence Tao idevágó [10,11] bejegyzéseit.)

Douglas faktorizációs tétele. Legyen $ \mathcal{H}$ valós vagy komplex Hilbert-tér, legyen továbbá $ A,B\colon \mathcal{H}\to\mathcal{H}$ folytonos lineáris operátor. Ekkor a következő kijelentések egyenértékűek:

(i) létezik olyan $ D\colon \mathcal{H}\to\mathcal{H}$ folytonos lineáris operátor, hogy $ BD=A$,

(ii) létezik olyan $ c\geq0$ konstans, hogy

$\displaystyle \Vert A^*x\Vert \leq c\cdot\Vert B^*x\Vert ,\qquad (\forall x\in\mathcal{H}), $

(iii) $ A$ és $ B$ képtereire fennáll a $ \operatorname{ran}A\subseteq \operatorname{ran}B$ tartalmazás.

Bizonyítás. Az könnyen adódik, hogy az (i) állítás maga után vonja (ii)-t és (iii)-at. Valóban, a $ c=\Vert D^*\Vert _{\mathrm{op}}$ választással azt látjuk, hogy

$\displaystyle \Vert A^*x\Vert=\Vert(BD)^*x\Vert=\Vert D^*B^*x\Vert\leq\Vert D^*\Vert _{\mathrm{op}}\cdot\Vert B^*x\Vert=c\cdot\Vert B^*x\Vert. $

Hasonlóan egyszerűen, a képtér definíciójába behelyettesítve azt kapjuk, hogy

$\displaystyle \operatorname{ran}A=\operatorname{ran}BD=\big\{BDx\mid x\in \math... ...big\}=\big\{By\mid y\in \operatorname{ran}D\big\}\subseteq\operatorname{ran}B. $

Belátjuk most az eredetileg Halmostól származó (ii) $ \Rightarrow$(i) implikációt. Tekintsük a $ \operatorname{ran}B^* \subseteq \mathcal{H}$ altéren a 

hozzárendeléssel értelmezett $ C^{}_0\colon \operatorname{ran}B^* \to\mathcal{H}$ leképezést. A (ii) feltétel szerint $ C^{}_0$ jóldefinált folytonos lineáris operátor, éspedig $ \Vert C^{}_0\Vert\leq c$, továbbá $ C^{}_0$ egyértelműen kiterjed ki a $ \overline{\operatorname{ran}B^*}$ altérre a linearitás valamint a norma megtartása mellett. Terjesszük tovább az így kapott operátort a $ \mathcal{H}$ Hilbert-tér egészére úgy, hogy a $ [\operatorname{ran}B^*]^{\perp}$ altéren 0-ként definiáljuk. Jelöljük $ C$-vel az így nyert operátort, és vegyük észre, hogy $ C$ lineáris. Emellett bármely $ x\in\mathcal{H}$ vektor előáll $ x=x^{}_0+x^{}_1$ alakban, ahol $ x^{}_0\in\overline{\operatorname{ran}B^* }$, $ x^{}_1\in [\operatorname{ran}B^*]^{\perp}$, így a

$\displaystyle \Vert Cx\Vert^2=\Vert C^{}_0x^{}_0\Vert^2\leq c^2\Vert x^{}_0\Vert^2\leq c^2\Vert x\Vert^2 $

becslésből látható, hogy $ C$ folytonos és $ \Vert C\Vert\leq c$. Végezetül a konstrukció alapján következik, hogy $ A^*=CB^*$, így $ D\coloneqq C^*$ választással $ A=BD$.

Most belátjuk a (iii) $ \Rightarrow$(i) implikációt. Legyen $ x\in\mathcal{H}$ tetszőleges rögzített vektor, akkor $ Ax\in \operatorname{ran}B$ figyelembevételével létezik egyetlen $ z=:D(x)\in[\ker B]^{\perp}$, hogy

$\displaystyle BD(x)=Ax.$ (1)

 

Elsőként igazoljuk, hogy az így definiált $ D\colon \mathcal{H}\to\mathcal{H}$ függvény lineáris: legyen ui. $ x,y\in\mathcal{H}$ tetszőleges, akkor $ D(x)+D(y), D(x+y)\in[\ker B]^{\perp}$ olyan vektorok, hogy

$\displaystyle B(D(x)+D(y))=Ax+Ay=A(x+y)=BD(x+y), $

következésképp $ D(x)+D(y)=D(x+y)$. Hasonlóképp igazolható $ D$ homogenitása. Mivel (1) szerint $ BD=A$, azért a tétel igazolva lesz, ha megmutatjuk, hogy $ D$ folytonos. A Banach-féle zártgráf tétel értelmében elegendő azt megmutatni, hogy $ D$ gráfja zárt. Legyen $ (x_n)\subset \mathcal{H}$ olyan sorozat, hogy $ x_n\to 0$ és $ Dx_n\to y$. Azt kell igazolnunk, hogy $ y=0$. Az $ A$ és $ B$ operátorok folytonossága miatt $ BDx_n=Ax_n\to0$, illetve $ BDx_n\to By$, vagyis $ By=0$. Ugyanakkor $ Dx_n\in[\ker B]^{\perp}$ miatt $ y\in[\ker B]^\perp$, így $ By=0$ miatt $ y=0$. Ezzel megmutattuk, hogy $ D$ folytonos, és hogy $ BD=A$.  $ \blacksquare$

Megjegyzés: A bizonyításból látható, hogy a tétel feltételei mellett az $ A=BX$ operátoregyenletnek eleget tevő $ D$ megoldás megválasztható úgy is, hogy $ \operatorname{ran}D\subseteq [\ker B]^{\perp}$ teljesüljön. E további feltétel mellett $ D$ egyértelmű is, és a normája egyenlő azzal a legkisebb $ c\geq0$ számmal, amely mellett (ii) fennáll. Ezt a $ D$ operátort szokás az $ BX=A$ egyenlet Douglas-megoldásának is nevezni.

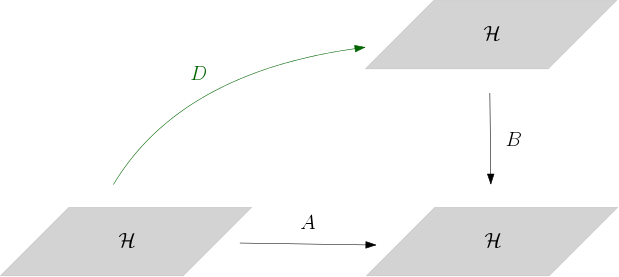
A faktorizációs lemma egyik szépsége annak egyszerűségében rejlik. Megértéséhez, illetve bizonyításához elegendő a tudományterület (azaz a funkcionálanalízis) legalapvetőbb fogalmait ismerni. Hogy mitől annyira hatékony maga a lemma, az talán azzal magyarázható, hogy három nagyon különbözöző feltételt kapcsol össze: az (i) tulajdonság tisztán algebrai jellegű, a (ii) egy metrikus egyenlőtlenség, míg (iii) egy egyszerű halmazelméleti tartalmazás. Megjegyezzük, hogy a (ii) feltételben lévő egyenlőtlenséget írhattuk volna úgy is, hogy

$\displaystyle \langle AA^*x,x\rangle\leq c^2\langle BB^*x,x\rangle, $

azaz a faktorizálhatóság még a pozitív operátorok rendezésével is kapcsolatba hozható.

A cikk lezárásaként az alábbiakban bemutatjuk Douglas eredményének egy érdekes és hasznos elméleti következményét, a Moore–Penrose-féle pszeudoinverz létezését. Az általánosított inverz ilyen fogalma komoly szerepet játszik többek között a biológiai alkalmazásokban és a mérnöki tudományokban. Az alkalmazások teljes spektrumát itt meg sem próbáljuk bemutatni, de az érdekesség kedvéért megemlítjük a digitális képhelyreállítási algoritmusokat, vagy éppen biochipek hiányzó vagy sérült adatainak becslését.

A Moore–Penrose-féle pszeudoinverz. Adott $ B$ korlátos operátor és $ b\in \mathcal{H}$ vektor mellett tekintsük a

$\displaystyle Bx=b$ (2)

lineáris egyenletet. Ez pontosan akkor oldható meg minden $ b\in \mathcal{H}$ jobb oldal mellett, ha $ B$ szürjektív, a megoldás egyértelműsége pedig ekvivalens $ B$ injektivitásával, vagyis a $ \ker B=\{0\}$ feltétellel. (Véges dimenziós $ \mathcal{H}$ esetén az injektivitás és szürjektivitás egymással egyenértékű tulajdonságok, végtelen dimenzióban viszont ezek egymásától függetlenek.) Ilyenkor az egyértelmű megoldást az $ x=B^{-1}b$ vektor adja, ahol $ B^{-1}$ szintén korlátos operátor.

Az általános esetben azonban $ B$ sem nem szürjektív, sem nem injektív. Ilyenkor a (2) egyenlet megoldhatósága ekvivalens azzal, hogy $ b\in\operatorname{ran}B$. A megoldás viszont csak a további $ x\in[\ker B]^{\perp}$ feltétel mellett lesz egyértelmű. Kérdés, hogy ha nincs inverz, akkor hogyan kaphatjuk meg a megoldó operátort? A Douglas-lemma alkalmazásaként az alábbiakban erre adunk választ.

Tekintsük ugyanis a $ \operatorname{ran}B\subseteq \mathcal{H}$ lineáris alteret. Ha ez zárt, akkor vehetjük az erre vett $ P\colon \mathcal{H}\to \operatorname{ran}B$ ortogonális projekciót, azaz azt az egyetlen $ P$ operátort, amelyre $ P=P^*=P^2$ és $ \operatorname{ran}P=\operatorname{ran}B$ egyaránt teljesül. Ekkor Douglas fenti faktorizációs lemmája és az azt követő megjegyzés értelmében létezik egyetlen $ B^{\dagger}$ szimbólummal jelölt korlátos operátor $ \mathcal{H}$-n, hogy

$\displaystyle BB^{\dagger}=P$   és$\displaystyle \qquad \operatorname{ran}B^{\dagger}\subseteq [\ker B]^\perp. $

Jelölje $ Q$ a $ [\ker B]^{\perp}$-re vett ortogonális projekciót. Könnyű bebizonyítani, hogy a $ B^{\dagger}$ operátor rendelkezik az alábbi tulajdonságokkal:

$\displaystyle BB^{\dagger}B=B,\qquad B^{\dagger}BB^{\dagger}=B^{\dagger},\qquad BB^{\dagger}=P,\qquad B^{\dagger}B=Q. $

A $ B^{\dagger}$ operátort a $ B$ Moore-Penrose-féle pszeudoinverzének nevezzük.

Vegyük észre, hogy $ B^{\dagger}$ értelmezésénél lényeges volt, hogy $ B$ képtere zárt, ugyanis merőleges vetítés csak zárt altérre vehető. Természetesen véges dimenziós terekben (Moore [7] és Penrose [8] ilyeneket vizsgáltak) ez a feltétel automatikusan teljesül.

Halmos Pál fényképe Roger Penrose-ról 

Végezetül térjünk vissza a (2) egyenlethez. Tegyük fel, hogy $ B$ képtere zárt. Ha $ b\in\operatorname{ran}B$, akkor a Moore–Penrose-inverz tulajdonságai alapján $ x=B^{\dagger}b$ választással

$\displaystyle Bx=BB^{\dagger}b=Pb=b $

teljesül, vagyis $ B^{\dagger}b\in[\ker B]^{\perp}$ megoldása a (2) egyenletnek.

Zárásként megemlítjük, hogy a Douglas-lemma egy változata érvényben marad a Hilbert-tereknél általánosabb struktúrákban is, nevezetesen Banach-terekben [1,6], ahol a vektorok hosszát nem skaláris szorzattal, hanem egy ún. normafüggvénnyel definiáljuk. Ennek az általánosításnak azonban ára van: skaláris szorzat híján a merőleges fogalmát sem tudjuk értelmezni, emiatt a Banach-terek geometriája jóval bonyolultabb. A Douglas-lemma is csak gyengébb formában marad érvényes [3], így annak alkalmazásai sem annyira széleskörűek.

A cikk az Emberi Erőforrások Minisztériumának ÚNKP-18-4-BGE-3 kódszámú „Új Nemzeti Kiválóság Program”, és a Nemzeti Fejlesztési, Kutatási és Innovációs Hivatal (NKFIH PD128374 és K115383) támogatásával készült.

Irodalomjegyzék

[1] B. A. Barnes, Majorization, range inclusion, and factorization for bounded linear operators, Proc. Amer. Math. Soc., 133 (2005), 155–162.

 

[2] J. Beery and C. Mead, Who's That Mathematician? – Paul R. Halmos Collection, Convergence, (January 2012), https://www.maa.org/book/export/html/117776, DOI:10.4169/loci003801.

 

[3] R. Bouldin, A counterexample in the factorization of Banach space operators, Proc. Amer. Math. Soc., 68 (1978), 327.

 

[4] R. G. Douglas, On majorization, factorization, and range inclusion of operators on Hilbert space, Proc. Amer. Math. Soc., 17 (1966), 413–415.

 

[5] R. G. Douglas, Banach algebra techniques in operator theory. Pure and Applied Mathematics, Vol. 49. Academic Press, New York-London, 1972.

 

[6] M. R. Embry, Factorization of operators on Banach space, Proc. Amer. Math. Soc., 38 (1973), 587–590.

 

[7] E. H. Moore, On the reciprocal of the general algebraic matrix, Bull. Amer. Math. Soc., 26:394–395, 1920.

 

[8] R. Penrose, A generalized inverse for matrices, Proc. Cambridge Philos. Soc., 51, (1955). 406–413.

 

[9] F. Riesz, http://www.bibl.u-szeged.hu/exhib/evfordulo/riesz/riesz.htm

 

[10] T. Tao, The closed graph theorem in various categories, https://terrytao.wordpress.com/2012/11/20/the-closed-graph-theorem-in-various-categories/

 

[11] T. Tao, The Baire category theorem and its Banach space consequences https://terrytao.wordpress.com/2009/02/01/245b-notes-9-the-baire-category-theorem-and-its-banach-space-consequences/
 
Tarcsay Zsigmond
Eötvös Loránd Tudományegyetem
Természettudományi Kar
Alkalmazott Analízis és Számításmatematikai Tanszék

 
Titkos Tamás
MTA Rényi Alfréd Matematikai Kutatóintézet
és Budapesti Gazdasági Egyetem

 

 

 

 

 

matematikatörténet analízis