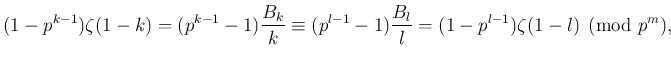1. Bevezetés
Andrew Wiles már a Fermat-sejtés bizonyítása előtt is híres matematikus volt. Kiemelkedő jelentőségű az Iwasawa-elméleti munkássága, melynek célja komplex ![]() -függvények (a Riemann-féle
-függvények (a Riemann-féle ![]() -függvény általánosításai) és különböző aritmetikai objektumok közötti kapcsolat létesítése. Ebben a cikkben ezt próbáljuk elmagyarázni a legegyszerűbb esetben, amikor az aritmetikai objektum az ún. Tate-motívum (ami lényegében az egységgyökök aritmetikáját írja le), az alaptest a racionális számok teste, a komplex
-függvény általánosításai) és különböző aritmetikai objektumok közötti kapcsolat létesítése. Ebben a cikkben ezt próbáljuk elmagyarázni a legegyszerűbb esetben, amikor az aritmetikai objektum az ún. Tate-motívum (ami lényegében az egységgyökök aritmetikáját írja le), az alaptest a racionális számok teste, a komplex ![]() -függvény pedig a Riemann-féle
-függvény pedig a Riemann-féle ![]() -függvény. Az Iwasawa-fősejtés bizonyítása ebben a legegyszerűbb esetben Wiles és Barry Mazur közös eredménye, de Wiles ezt általánosította a racionális számok helyett tetszőleges teljesen valós számtestre is (azaz olyan
-függvény. Az Iwasawa-fősejtés bizonyítása ebben a legegyszerűbb esetben Wiles és Barry Mazur közös eredménye, de Wiles ezt általánosította a racionális számok helyett tetszőleges teljesen valós számtestre is (azaz olyan ![]() bővítésekre, hogy
bővítésekre, hogy ![]() minimálpolinomjának minden komplex gyöke valós). Továbbá Wiles témavezetőjével, John Coatesszal közösen igazolta az Iwasawa-fősejtést komplex szorzással (egyfajta ritka, de fontos szimmetriával) rendelkező elliptikus görbékre is, mely a legelső fontos részeredmény volt az azóta milleniumi egymilliódolláros problémává avanzsáló Birch–Swinnerton-Dyer-sejtésre.
minimálpolinomjának minden komplex gyöke valós). Továbbá Wiles témavezetőjével, John Coatesszal közösen igazolta az Iwasawa-fősejtést komplex szorzással (egyfajta ritka, de fontos szimmetriával) rendelkező elliptikus görbékre is, mely a legelső fontos részeredmény volt az azóta milleniumi egymilliódolláros problémává avanzsáló Birch–Swinnerton-Dyer-sejtésre.
2. Fermat-tól Kummerig
Mint az algebrai számelméletben szinte mindennek, az Iwasawa elmélet gyökerei is a Fermat-sejtés – mely szerint az ![]() egyenletnek nincsenek nemtriviális megoldásai, ha
egyenletnek nincsenek nemtriviális megoldásai, ha ![]() – bizonyítására adott korai próbálkozásokban vannak. Nyilvánvaló, hogy a sejtést elég bebizonyítani abban az esetben, amikor
– bizonyítására adott korai próbálkozásokban vannak. Nyilvánvaló, hogy a sejtést elég bebizonyítani abban az esetben, amikor ![]() , vagy
, vagy ![]() egy páratlan prímszám. Maga Fermat az
egy páratlan prímszám. Maga Fermat az ![]() esetre bizonyítást adott egy későbbi levelében. Euler az
esetre bizonyítást adott egy későbbi levelében. Euler az ![]() (1770), Dirichlet az
(1770), Dirichlet az ![]() esetet bizonyította (1828).
esetet bizonyította (1828).
Ezek az elszigetelt esetek is rámutattak arra, hogy a Fermat-sejtésben két esetet érdemes megkülönböztetni: az ún. első esetet, amikor ![]() nem osztja az
nem osztja az ![]() számok egyikét sem, illetve a második esetet, amikor
számok egyikét sem, illetve a második esetet, amikor ![]() osztja valamelyiket, (amennyiben az
osztja valamelyiket, (amennyiben az ![]() és
és ![]() számok relatív prímek, ami feltehető, akkor pontosan egyet).
számok relatív prímek, ami feltehető, akkor pontosan egyet).
Az első általános tétel, ami több, mint egy exponensről mond valamit, Sophie Germain1 nevéhez fűződik: ha ![]() egy olyan prím, hogy
egy olyan prím, hogy ![]() szintén prím, akkor a Fermat-tétel első esete igaz
szintén prím, akkor a Fermat-tétel első esete igaz ![]() -re. Germain módszerét általánosítva Legendre megmutatta, hogy az első eset igaz minden
-re. Germain módszerét általánosítva Legendre megmutatta, hogy az első eset igaz minden ![]() prímre.
prímre.
Az ![]() eset nehéznek bizonyult. Az első bizonyítás Lame nevéhez fűződik (1839). A korabeli matematikusok Cauchy, Lame, és mások több cikkben tökéletesítették módszereiket, és 1847-ben Lame a Francia Akadémián bejelentette, hogy belátta a Fermat sejtést. Liouville azonban rámutatott, hogy a bizonyítás, amely az ún. körosztási testek egészeinek számelméletén alapszik, felhasználja a prímfelbontás tételét, ami ebben a gyűrűben bizonyításra szorul. Valójában, egy másik problémán dolgozva, Kummer már 1846-ban megmutatta, hogy a 23-adik egységgyökökkel képzett gyűrűben nem igaz a számelmélet alaptétele, és így Lame2 bizonyítása sem működhet.
eset nehéznek bizonyult. Az első bizonyítás Lame nevéhez fűződik (1839). A korabeli matematikusok Cauchy, Lame, és mások több cikkben tökéletesítették módszereiket, és 1847-ben Lame a Francia Akadémián bejelentette, hogy belátta a Fermat sejtést. Liouville azonban rámutatott, hogy a bizonyítás, amely az ún. körosztási testek egészeinek számelméletén alapszik, felhasználja a prímfelbontás tételét, ami ebben a gyűrűben bizonyításra szorul. Valójában, egy másik problémán dolgozva, Kummer már 1846-ban megmutatta, hogy a 23-adik egységgyökökkel képzett gyűrűben nem igaz a számelmélet alaptétele, és így Lame2 bizonyítása sem működhet.
Kummer azonban ennél jóval többet bizonyított, bevezette az ideális számok elméletét, és ennek segítségével igazolta a következőket. Legyen ![]() és
és ![]() . Az
. Az ![]() gyűrű két ideálja
gyűrű két ideálja ![]() legyen ekvivalens, ha van olyan
legyen ekvivalens, ha van olyan ![]() ,
, ![]() , hogy
, hogy ![]() . Kummer egyik legfontosabb felfedezése, hogy a számelmélet alaptétele az ideálok bevezetésével megmenthető, továbbá annak bizonyítása, hogy a fenti ekvivalencia-reláció véges sok osztályra bontja az
. Kummer egyik legfontosabb felfedezése, hogy a számelmélet alaptétele az ideálok bevezetésével megmenthető, továbbá annak bizonyítása, hogy a fenti ekvivalencia-reláció véges sok osztályra bontja az ![]() gyűrű ideáljait. A továbbiakban jelölje az osztályok számát
gyűrű ideáljait. A továbbiakban jelölje az osztályok számát ![]() .
.
A Fermat-sejtéssel kapcsolatban Kummer fő eredménye a következő. Legyen ![]() egy olyan prím, hogy
egy olyan prím, hogy ![]() nem osztja a
nem osztja a ![]() osztályszámot (ezeket reguláris prímeknek hívjuk). Ha
osztályszámot (ezeket reguláris prímeknek hívjuk). Ha ![]() reguláris, akkor az
reguláris, akkor az ![]() egyenletnek az egész számok körében nincs olyan megoldása, melyre
egyenletnek az egész számok körében nincs olyan megoldása, melyre ![]() . Azóta is megoldatlan kérdés, hogy létezik-e végtelen sok reguláris prím – azt viszont tudjuk3, hogy végtelen sok irreguláris prím van (a legkisebb a 37). Viszont heurisztikus gondolatmenetek azt mutatják, hogy a prímek kb.
. Azóta is megoldatlan kérdés, hogy létezik-e végtelen sok reguláris prím – azt viszont tudjuk3, hogy végtelen sok irreguláris prím van (a legkisebb a 37). Viszont heurisztikus gondolatmenetek azt mutatják, hogy a prímek kb. ![]() -a reguláris – ez Siegel sejtése (1964).
-a reguláris – ez Siegel sejtése (1964).
Ezen túlmenően Kummer kapcsolatot talált a ![]() osztályszám és a Riemann-
osztályszám és a Riemann-![]() függvény negatív egész helyeken felvett értékei között. Ennek segítségével a
függvény negatív egész helyeken felvett értékei között. Ennek segítségével a ![]() osztályszám
osztályszám ![]() -vel való oszthatóságára a következő kritériumot adta:
-vel való oszthatóságára a következő kritériumot adta: ![]() pontosan akkor reguláris prím, ha
pontosan akkor reguláris prím, ha ![]() nem osztja a
nem osztja a ![]() Bernoulli szám egyszerűsített alakjának számlálóját semmilyen
Bernoulli szám egyszerűsített alakjának számlálóját semmilyen ![]() páros számra sem.
páros számra sem.
Az alapfogalmakban jártas olvasó innen folytathatja az 5. fejezettel, átugorva a 3. és 4. fejezeteket.
3. Riemann ![]() -értékek
-értékek
A ![]() -függvény,
-függvény, ![]() konvergens ha
konvergens ha ![]() valós. Riemann megmutatta, hogy ez a függvény természetes módon kiterjeszthető komplex értékekre, az
valós. Riemann megmutatta, hogy ez a függvény természetes módon kiterjeszthető komplex értékekre, az ![]() kivételével, és a kiterjesztett függvény zérushelyei pontos információval rendelkeznek a prímszámok eloszlásáról. Ezen alapvető észrevételeiért a függvényt Riemann-féle
kivételével, és a kiterjesztett függvény zérushelyei pontos információval rendelkeznek a prímszámok eloszlásáról. Ezen alapvető észrevételeiért a függvényt Riemann-féle ![]() -függvénynek hívjuk.
-függvénynek hívjuk.
Már jóval korábban, az analízis születésekor izgalmas kérdés volt ![]() értéke. Ezt Euler határozta meg,
értéke. Ezt Euler határozta meg, ![]() . Euler e munkáját kiteljesítette, belátta, hogy
. Euler e munkáját kiteljesítette, belátta, hogy ![]() . Itt a
. Itt a ![]() Bernoulli számok a következőképpen adhatók meg. Legyen
Bernoulli számok a következőképpen adhatók meg. Legyen
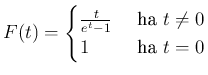
ekkor ![]() , azaz az
, azaz az ![]() függvény
függvény ![]() -adik deriváltja
-adik deriváltja ![]() -ban. Ekvivalens módon
-ban. Ekvivalens módon ![]() , és így a Bernoulli számok az
, és így a Bernoulli számok az ![]() egyenletből rekurzívan számíthatók. Feladat: Igazoljuk, hogy
egyenletből rekurzívan számíthatók. Feladat: Igazoljuk, hogy ![]() , ha
, ha ![]() páratlan.
páratlan.
Euler ezen túlmenően észrevette, hogy, ha a ![]() -függvény valamilyen természetes módon értelmezhető lenne negatív egészeken, akkor a
-függvény valamilyen természetes módon értelmezhető lenne negatív egészeken, akkor a ![]() és
és ![]() értékek között egy egyszerű kapcsolat áll fenn. Ezt a szimmetriát Riemann munkája után a
értékek között egy egyszerű kapcsolat áll fenn. Ezt a szimmetriát Riemann munkája után a ![]() -függvény függvényegyenletének hívjuk. Euler speciális eredménye a
-függvény függvényegyenletének hívjuk. Euler speciális eredménye a
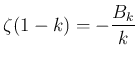
összefüggés, ha ![]() páros.
páros.
Euler ötlete a következő. A 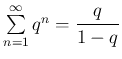 azonosságban a
azonosságban a ![]() helyettesítés után az
helyettesítés után az 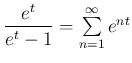 azonosságot kapjuk, ami értelmes és igaz minden
azonosságot kapjuk, ami értelmes és igaz minden ![]() valós számra. Ha az így kapott azonosságot
valós számra. Ha az így kapott azonosságot ![]() -szor deriváljuk, és utána az értelmezési határon lévő
-szor deriváljuk, és utána az értelmezési határon lévő ![]() -t helyettesítünk, akkor
-t helyettesítünk, akkor 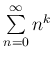 -ra kapnánk értéket. Ez persze ebben a formában még nem alkalmazható, hisz két értelmetlen mennyiség között fennálló formális azonosságot ad. Ehelyett Euler a következő trükkel élt
-ra kapnánk értéket. Ez persze ebben a formában még nem alkalmazható, hisz két értelmetlen mennyiség között fennálló formális azonosságot ad. Ehelyett Euler a következő trükkel élt
Ebből átrendezés után az előbbi helyettesítést alkalmazva
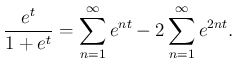
Itt a bal oldalon álló függvény már értelmes ![]() környezetében, és így
környezetében, és így ![]() -szor deriválva a
-szor deriválva a
![$\displaystyle \left[\left(\frac{d}{dt}\right)^k \left(\frac{e^t}{e^t+1}\right)\right]_{t=0} = (1-2^{k+1}) \sum_{n=1}^{\infty }n^k
$](/images/stories/latex/21da16faf9ea2c8da2ed92b0245a98bf_iwasawa/img57.png)
azonosságot kapjuk, ahol persze a jobb oldal értelmetlen, de Euler ezzel a módszerrel definiálja. Pl. ![]() esetében Euler jelölése szerint
esetében Euler jelölése szerint
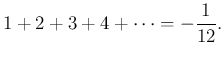
A ![]() azonossághoz csak az
azonossághoz csak az ![]() függvény 0 körüli Taylor-sorát kell kifejezni a Bernoulli-számok segítségével, (ami viszonylag könnyen megtehető, felhasználva, hogy
függvény 0 körüli Taylor-sorát kell kifejezni a Bernoulli-számok segítségével, (ami viszonylag könnyen megtehető, felhasználva, hogy ![]() páratlan).
páratlan).
Euler fenti felfedezése a Riemann-féle kiterjesztés segítségével válik majd pontossá.
4. 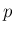 -adikus számok
-adikus számok
Mint ahogy a valós számok legintuitívabb bevezetése a végtelen tizedestörteken keresztül történik, a ![]() -adikus számokat is legegyszerűbb végtelen
-adikus számokat is legegyszerűbb végtelen ![]() -hatványösszegekként felfogni. Ugyanakkor egy elsőre furcsának tűnő változtatást végzünk, egy
-hatványösszegekként felfogni. Ugyanakkor egy elsőre furcsának tűnő változtatást végzünk, egy ![]() -adikus szám
-adikus szám
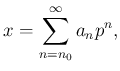
ahol az ![]() számjegyek a
számjegyek a ![]() értékek körül kerülnek ki. Fontos, hogy itt most a kitevők tetszőlegesen nagyok lehetnek. Ebben a világban
értékek körül kerülnek ki. Fontos, hogy itt most a kitevők tetszőlegesen nagyok lehetnek. Ebben a világban ![]() fog fennállni, és
fog fennállni, és ![]() lesz divergens. A
lesz divergens. A ![]() -adikus számok összességét
-adikus számok összességét ![]() , azon
, azon ![]() -adikus számok halmazát, amelyek csak nemnegatív
-adikus számok halmazát, amelyek csak nemnegatív ![]() -hatványt tartalmaznak
-hatványt tartalmaznak ![]() jelöli. Érdemes meggondolni, hogy a fenti formális végtelen összegek összeadása vagy szorzása az általános iskolában megszokott módszerrel, a maradékok helyiértékes továbbvitelével, könnyen definiálható, és így
jelöli. Érdemes meggondolni, hogy a fenti formális végtelen összegek összeadása vagy szorzása az általános iskolában megszokott módszerrel, a maradékok helyiértékes továbbvitelével, könnyen definiálható, és így ![]() egy gyűrű. Tehát bármilyen meglepő, nincs szükség előjelre, például
egy gyűrű. Tehát bármilyen meglepő, nincs szükség előjelre, például 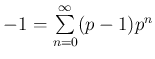 .
.
Ugyanakkor jogosan merül fel a kérdés, hogy ez az önmagában esztétikus matematikai rendszer mire hasznos. Az nyilvánvaló, hogy klasszikus geometriára nem, a geometria számszerűsítésében a negatív hatványok a kicsik – bár van olyan fizikai elmélet, mely szerint a kis távolságokban a tér nem a valós számokhoz, hanem a ![]() -adikusakhoz hasonlóan viselkedik4. Habár a halmazelmélet szempontjából a
-adikusakhoz hasonlóan viselkedik4. Habár a halmazelmélet szempontjából a ![]() intervallum ugyanakkora mint a
intervallum ugyanakkora mint a ![]() intervallum, a geometriai intuíció szerint a
intervallum, a geometriai intuíció szerint a ![]() intervallum lényegesen kevesebb helyet foglal el. Nyilvánvaló, hogy jóval több információnk van egy hosszról, ha tudjuk, hogy kisebb mint
intervallum lényegesen kevesebb helyet foglal el. Nyilvánvaló, hogy jóval több információnk van egy hosszról, ha tudjuk, hogy kisebb mint ![]() , mintha csak azt tudnánk róla, hogy kisebb, mint 100.
, mintha csak azt tudnánk róla, hogy kisebb, mint 100.
Az egész számok halmazán ugyanígy joggal gondolhatjuk a 9-cel osztható számokról, hogy egy kisebb hányadát alkotják a számoknak5. Ezt az információt egy újfajta, aritmetikus és nem geometriai metrika bevezetésével fejezhetjük ki. Legyen ![]() , ahol
, ahol ![]() , ha
, ha ![]() osztható
osztható ![]() -nel, de
-nel, de ![]() -gyel már nem. A
-gyel már nem. A ![]() metrikát definiál
metrikát definiál ![]() -n, és a
-n, és a ![]() -adikus egészek
-adikus egészek ![]() gyűrűje
gyűrűje ![]() teljessé tétele ebben a metrikában.
teljessé tétele ebben a metrikában.
A ![]() -adikus számok tehát a
-adikus számok tehát a ![]() hatványok szerinti kongruenciák vizsgálatában játszik fontos szerepet. Egy fontos konkrét alkalmazás a következő. Egyszerű akadálya egy számelméleti egyenlet megoldhatóságának, ha már valamely egész szerinti maradékok vizsgálata kimutatja, hogy az egyenlet kielégíthetetlen. Ha
hatványok szerinti kongruenciák vizsgálatában játszik fontos szerepet. Egy fontos konkrét alkalmazás a következő. Egyszerű akadálya egy számelméleti egyenlet megoldhatóságának, ha már valamely egész szerinti maradékok vizsgálata kimutatja, hogy az egyenlet kielégíthetetlen. Ha ![]() , akkor a kínai maradéktétel szerint már valamely prímhatványra sincs megoldás. Ennek a módszernek a szofisztikáltabb változata az ún. lokális-globális elv, ami központi szerepet játszik a modern algebrai számelméletben. Vegyük észre, hogy nem elég prímmodulusokat nézni: pl. az
, akkor a kínai maradéktétel szerint már valamely prímhatványra sincs megoldás. Ennek a módszernek a szofisztikáltabb változata az ún. lokális-globális elv, ami központi szerepet játszik a modern algebrai számelméletben. Vegyük észre, hogy nem elég prímmodulusokat nézni: pl. az
egyenletnek modulo 3 létezik nem-triviális megoldása (jelesül a ![]() ), és mod 9 is, de már csak olyan, amiben
), és mod 9 is, de már csak olyan, amiben ![]() ,
, ![]() , és
, és ![]() is osztható 3-mal (feladat az olvasónak: miért is?). Persze a szó eredeti értelmében tetszőleges
is osztható 3-mal (feladat az olvasónak: miért is?). Persze a szó eredeti értelmében tetszőleges ![]() -re létezik olyan megoldás mod
-re létezik olyan megoldás mod ![]() , mely nem csupa 0-kból áll, de minden ilyen megoldásra
, mely nem csupa 0-kból áll, de minden ilyen megoldásra ![]() osztója kell legyen
osztója kell legyen ![]() és
és ![]() mindegyikének. Ha
mindegyikének. Ha ![]() -nel tartunk a végtelenbe, akkor ezek a megoldások
-nel tartunk a végtelenbe, akkor ezek a megoldások ![]() -ban már csupa 0-vá válnak, tehát a fenti egyenletnek nem lehet nem-triviális racionális megoldása sem. A
-ban már csupa 0-vá válnak, tehát a fenti egyenletnek nem lehet nem-triviális racionális megoldása sem. A ![]() -adikus számok tehát lehetővé teszik, hogy a
-adikus számok tehát lehetővé teszik, hogy a ![]() prím egyre növekvő hatványai szerinti maradékosztályok gyűrűjét egyetlen nagy gyűrűbe foglaljuk össze, ezek a
prím egyre növekvő hatványai szerinti maradékosztályok gyűrűjét egyetlen nagy gyűrűbe foglaljuk össze, ezek a ![]() -adikus egészek.
-adikus egészek.
Bár a ![]() -adikus számok axiomatikus megalapozása terjedelmes, a tételek és bizonyítások technikailag sokkal egyszerűbbek, mint a valós számok esetében. Az érdeklődő olvasó könnyen megtalálja az elmélet kifejtését pl. Gouvêa:
-adikus számok axiomatikus megalapozása terjedelmes, a tételek és bizonyítások technikailag sokkal egyszerűbbek, mint a valós számok esetében. Az érdeklődő olvasó könnyen megtalálja az elmélet kifejtését pl. Gouvêa: ![]() -adic Numbers, An Introduction Springer (1997) könyvében.
-adic Numbers, An Introduction Springer (1997) könyvében.
5. Mi is az a ![]() -adikus
-adikus ![]() -függvény?
-függvény?
Kummer a 19. század végén nemcsak azt vette észre, hogy a Riemann-féle ![]() -függvény negatív egész helyeken felvett értékei és a körosztási testek osztályszáma között összefüggés van. Az ő nevéhez fűződnek a következő kongruenciák a Bernoulli-számokra:
-függvény negatív egész helyeken felvett értékei és a körosztási testek osztályszáma között összefüggés van. Az ő nevéhez fűződnek a következő kongruenciák a Bernoulli-számokra:
ha ![]() , ahol
, ahol ![]() az Euler-féle
az Euler-féle ![]() -függvény. Ezt úgy kell érteni, hogy a két oldalon álló racionális számok nevezője nem osztható
-függvény. Ezt úgy kell érteni, hogy a két oldalon álló racionális számok nevezője nem osztható ![]() -vel, ezért tekinthetjük mindkét oldalt modulo
-vel, ezért tekinthetjük mindkét oldalt modulo ![]() .
.
A következő heurisztikus gondolatmenet szigorúan véve teljesen hibás, és nem is lehet ilyen formában precízzé tenni, de mégis rámutat arra, hogyan lehet egy ilyen Kummer-féle kongruenciát megsejteni. Induljunk ki a ( ![]() esetén értelmes)
esetén értelmes)
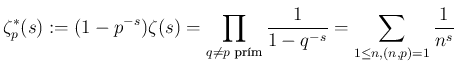
formulából: ez nem más, mint a módosított ![]() -függvény, ahol a
-függvény, ahol a ![]() -hez tartozó Euler-faktort kihagyjuk a szorzatból. Vegyük észre, hogy az Euler-Fermat tétel értelmében (mivel feltettük, hogy
-hez tartozó Euler-faktort kihagyjuk a szorzatból. Vegyük észre, hogy az Euler-Fermat tétel értelmében (mivel feltettük, hogy ![]() )
)
Ha ennek a végtelen sok kongruenciának a reciprokát összeadjuk, akkor
adódik. Sajnos ezzel a gondolatmenettel több bökkenő is van:
- egyrészt miért lehetne összeadni végtelen sok kongruenciát;
- másrészt ha
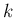 és
és  pozitív egészek, akkor
pozitív egészek, akkor 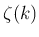 , ill.
, ill. 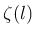 nem racionális, de még csak nem is algebrai szám – mi értelme lenne akkor egy ilyen kongruenciának?;
nem racionális, de még csak nem is algebrai szám – mi értelme lenne akkor egy ilyen kongruenciának?; - harmadrészt ha viszont negatív egész
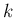 -t és
-t és  -et veszünk (ilyenkor
-et veszünk (ilyenkor 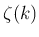 és
és 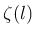 valóban racionális), és az 1. számú problémával valamilyen csodával határos módon megbírkózunk, akkor pedig az a baj, hogy a
valóban racionális), és az 1. számú problémával valamilyen csodával határos módon megbírkózunk, akkor pedig az a baj, hogy a 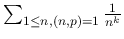 összeg nem konvergál.
összeg nem konvergál.
Annál inkább bámulatos, hogy az (1) kongruenciák mégis teljesülnek (legalábbis, ha ![]() )!
)!
Az (1) kongruenciát a következőképpen is interpretálhatjuk. Rögzítsünk egy ![]() nemnulla maradékot modulo
nemnulla maradékot modulo ![]() , azaz egy számot 1 és
, azaz egy számot 1 és ![]() között, továbbá egy
között, továbbá egy ![]()
![]() -adikus egész számot, azaz egy
-adikus egész számot, azaz egy ![]() formális összeget, ahol
formális összeget, ahol ![]() (
(![]() ). Szeretnénk a
). Szeretnénk a ![]() függvényt értelmezni (rögzített
függvényt értelmezni (rögzített ![]() esetén
esetén ![]() -ben
-ben ![]() -adikusan folytonosan) a
-adikusan folytonosan) a ![]() rendezett párra úgy, hogy a függvényérték egy
rendezett párra úgy, hogy a függvényérték egy ![]() -adikus szám legyen. Ha a függvényértéket valamilyen
-adikus szám legyen. Ha a függvényértéket valamilyen ![]() egészre modulo
egészre modulo ![]() szeretnénk megmondani, akkor ehhez vegyünk egy olyan
szeretnénk megmondani, akkor ehhez vegyünk egy olyan ![]() egész számot, amire
egész számot, amire
Ilyen persze létezik a kínai maradéktétel szerint, hiszen ![]() . Tekintsük a
. Tekintsük a ![]() számot. Vegyük észre, hogy az (1) kongruencia miatt
számot. Vegyük észre, hogy az (1) kongruencia miatt ![]() osztási maradéka modulo
osztási maradéka modulo ![]() nem függ
nem függ ![]() választásától. Így definiálhatjuk a
választásától. Így definiálhatjuk a ![]() szám
szám ![]() -gyel való osztási maradékát ennek a számnak! Végül ha
-gyel való osztási maradékát ennek a számnak! Végül ha ![]() -mel tartunk a végtelenbe, akkor kapunk egy
-mel tartunk a végtelenbe, akkor kapunk egy ![]() jóldefiniált
jóldefiniált ![]() -adikus számot. Ez a konstrukció Kubota és Leopoldt nevéhez fűződik 1964-ből.
-adikus számot. Ez a konstrukció Kubota és Leopoldt nevéhez fűződik 1964-ből.
Másszóval az ![]() -függvényt a negatív egész számokról ki tudtuk terjeszteni folytonosan
-függvényt a negatív egész számokról ki tudtuk terjeszteni folytonosan
azaz a ![]() -adikus egészek
-adikus egészek ![]() példányára.6 Rögzített
példányára.6 Rögzített ![]() esetén a kapott függvényt
esetén a kapott függvényt ![]() -vel jelöljük és a
-vel jelöljük és a ![]() -adikus
-adikus ![]() -függvény
-függvény ![]() -hez tartozó ágának nevezzük. Vegyük észre, hogy páros
-hez tartozó ágának nevezzük. Vegyük észre, hogy páros ![]() esetén ez a függvény azonosan 0, hiszen a Riemann-féle
esetén ez a függvény azonosan 0, hiszen a Riemann-féle ![]() -függvény eltűnik negatív páros egész helyeken. Igazi aritmetikai tartalmat tehát a páratlan
-függvény eltűnik negatív páros egész helyeken. Igazi aritmetikai tartalmat tehát a páratlan ![]() -hez tartozó ágak hordoznak.
-hez tartozó ágak hordoznak.
6. Az Iwasawa-fősejtés
Az Iwasawa-fősejtést Wiles 1984-ben Barry Mazurrel közösen bizonyította, majd 1990-ben egyedül is adott rá egy új bizonyítást általánosabb formában, nemcsak a racionális számok testére, hanem tetszőleges teljesen valós testre. Az állítás lényegében annak a precíz megfogalmazása, hogy milyen aritmetikai információt hordoznak a ![]()
![]() -adikus zeta-függvények. A pontos megfogalmazáshoz szükséges ismeretek összefoglalására ez a cikk túl szűk lenne. Az alábbi kitekintés erre az általános elméletre, reméljük, sok olvasóban kelti fel az érdeklődést a Galois-elmélet és a
-adikus zeta-függvények. A pontos megfogalmazáshoz szükséges ismeretek összefoglalására ez a cikk túl szűk lenne. Az alábbi kitekintés erre az általános elméletre, reméljük, sok olvasóban kelti fel az érdeklődést a Galois-elmélet és a ![]() -adikus analízis iránt. Az érdeklődő olvasó bevezető szinten olvashat a szükséges fogalmakról az alábbi egyetemi jegyzetben, az Iwasawa-fősejtés bizonyítását pedig Coates és Sujatha: Cyclotomic Fields and Zeta Values Springer (2006) könyvében találja.
-adikus analízis iránt. Az érdeklődő olvasó bevezető szinten olvashat a szükséges fogalmakról az alábbi egyetemi jegyzetben, az Iwasawa-fősejtés bizonyítását pedig Coates és Sujatha: Cyclotomic Fields and Zeta Values Springer (2006) könyvében találja.
Iwasawa 60-as években megfogalmazott észrevétele az volt, hogy – a sejtés szerint – ezen függvényekből nemcsak a ![]() -edik körosztási test, hanem minden
-edik körosztási test, hanem minden ![]() -re a
-re a ![]() -edik körosztási test osztályszámának
-edik körosztási test osztályszámának ![]() részét is meg lehet határozni. Az aritmetikai oldalon a kiindulópont a következő: Adott
részét is meg lehet határozni. Az aritmetikai oldalon a kiindulópont a következő: Adott ![]() -ra jelölje
-ra jelölje ![]() a
a ![]() körosztási test osztálycsoportjának
körosztási test osztálycsoportjának ![]() részét (azaz
részét (azaz ![]() -Sylow részcsoportját). Ezen hat a
-Sylow részcsoportját). Ezen hat a ![]() Galois csoport, továbbá minden
Galois csoport, továbbá minden ![]() -ra van egy természetes
-ra van egy természetes ![]() vetítő leképezés. Ha
vetítő leképezés. Ha ![]() -mel tartunk a végtelenbe, akkor vehetjük a
-mel tartunk a végtelenbe, akkor vehetjük a ![]() inverz limeszt, amin már a
inverz limeszt, amin már a ![]() -adikus egészek
-adikus egészek ![]() multiplikatív csoportja hat. Viszont itt
multiplikatív csoportja hat. Viszont itt ![]() izomorf a
izomorf a ![]() elemű test
elemű test ![]() multiplikatív csoportjának és a
multiplikatív csoportjának és a ![]() -adikus egészek
-adikus egészek ![]() additív csoportjának (nemkanonikus) direkt szorzatával. Itt
additív csoportjának (nemkanonikus) direkt szorzatával. Itt ![]() egy
egy ![]() -edrendű ciklikus csoport, melynek
-edrendű ciklikus csoport, melynek ![]() karakterisztikában minden végesdimenziós reprezentációja féligegyszerű, tehát egy
karakterisztikában minden végesdimenziós reprezentációja féligegyszerű, tehát egy ![]() -hatvány rendű Abel csoporton is karakterek direkt összegén keresztül hat. Továbbá ezen karakterek ugyanúgy a 0-tól
-hatvány rendű Abel csoporton is karakterek direkt összegén keresztül hat. Továbbá ezen karakterek ugyanúgy a 0-tól ![]() -ig terjedő egészekkel vannak indexelve, mint a
-ig terjedő egészekkel vannak indexelve, mint a ![]() -adikus zeta-függvény ágai, így van köztük egy (természetes) kölcsönösen egyértelmű megfeleltetés. A máig nyitott (és egyelőre elérhetetlen) Vandiver sejtés szerint a páros indexű karakterekhez tartozó izotipikus komponensei
-adikus zeta-függvény ágai, így van köztük egy (természetes) kölcsönösen egyértelmű megfeleltetés. A máig nyitott (és egyelőre elérhetetlen) Vandiver sejtés szerint a páros indexű karakterekhez tartozó izotipikus komponensei ![]() -nek triviálisak (azaz
-nek triviálisak (azaz ![]() -ben nincs olyan nemnulla elem, amin
-ben nincs olyan nemnulla elem, amin ![]() egy páros indexű karakteren keresztül hat). Ez azzal analóg, hogy a páros
egy páros indexű karakteren keresztül hat). Ez azzal analóg, hogy a páros ![]() -hez tartozó ágai a
-hez tartozó ágai a ![]() -adikus zeta-függvénynek azonosan 0-k, viszont ezen komponensekről nem mond semmit az Iwasawa fősejtés. Ugyanakkor a
-adikus zeta-függvénynek azonosan 0-k, viszont ezen komponensekről nem mond semmit az Iwasawa fősejtés. Ugyanakkor a ![]() csoport hatása
csoport hatása ![]() -n a konstrukcióból adódóan folytonos, így kiterjed a
-n a konstrukcióból adódóan folytonos, így kiterjed a ![]() telített csoportalgebrára (az ún. Iwasawa-algebrára), mivel
telített csoportalgebrára (az ún. Iwasawa-algebrára), mivel ![]() egy pro-
egy pro-![]() Abel csoport, speciálisan
Abel csoport, speciálisan ![]() -modulus is. Viszont a
-modulus is. Viszont a ![]() Iwasawa-algebrát (nemkanonikusan) azonosíthatjuk a
Iwasawa-algebrát (nemkanonikusan) azonosíthatjuk a ![]() feletti
feletti ![]() egyváltozós formális hatványsorgyűrűvel. Utóbbi egy kétdimenziós lokális gyűrű, ami feletti modulusoknak létezik – a főideálgyűrű feletti végesen generált modulusok klasszifikálásához hasonló – struktúraelmélete: a végesen generált torzió modulusokat pszeudo-izomorfizmus (jelen esetben véges elemszámú modulus) erejéig meghatározza a karakterisztikus ideáljuk (ami a véges Abel-csoport rendjével, illetve a négyzetes mátrixok karakterisztikus polinomjával analóg fogalom). Másrészt a
egyváltozós formális hatványsorgyűrűvel. Utóbbi egy kétdimenziós lokális gyűrű, ami feletti modulusoknak létezik – a főideálgyűrű feletti végesen generált modulusok klasszifikálásához hasonló – struktúraelmélete: a végesen generált torzió modulusokat pszeudo-izomorfizmus (jelen esetben véges elemszámú modulus) erejéig meghatározza a karakterisztikus ideáljuk (ami a véges Abel-csoport rendjével, illetve a négyzetes mátrixok karakterisztikus polinomjával analóg fogalom). Másrészt a ![]() -adikus zeta-függvény páratlan
-adikus zeta-függvény páratlan ![]() -hez tartozó ága is (formális) hatványsorba fejthető, tehát – lényegében – a
-hez tartozó ága is (formális) hatványsorba fejthető, tehát – lényegében – a ![]() gyűrű egy elemét definiálja. Az Iwasawa fősejtés azt mondja ki, hogy – megfelelő normalizáció mellett – a páratlan
gyűrű egy elemét definiálja. Az Iwasawa fősejtés azt mondja ki, hogy – megfelelő normalizáció mellett – a páratlan ![]() -hez tartozó
-hez tartozó ![]() -karakter
-karakter ![]() -beli izotipikus komponensének mint
-beli izotipikus komponensének mint ![]() -modulusnak a karakterisztikus ideálját a
-modulusnak a karakterisztikus ideálját a ![]() zeta-függvény mint
zeta-függvény mint ![]() -adikus hatványsor generálja.
-adikus hatványsor generálja.
Ez a – két látszólag teljesen különböző – objektumokat összekötő tétel összefoglalja mindazt, amit tudunk a Riemann-féle ![]() -függvény speciális értékei és a körosztási testek aritmetikája közti misztikus kapcsolatról. A sejtésnek léteznek olyan általánosításai, melyben az osztálycsoport szerepét elliptikus görbék
-függvény speciális értékei és a körosztási testek aritmetikája közti misztikus kapcsolatról. A sejtésnek léteznek olyan általánosításai, melyben az osztálycsoport szerepét elliptikus görbék ![]() -Selmer csoportja játssza, a Riemann-féle
-Selmer csoportja játssza, a Riemann-féle ![]() -függvény helyett pedig a görbe
-függvény helyett pedig a görbe ![]() -függvénye jön elő – ezeknek alapvetően fontos alkalmazásai vannak a Birch–Swinnerton-Dyer sejtés ismert eseteinek bizonyításában. Az elmélet új, manapság is folyamatosan fejlődő ága a nemkommutatív Iwasawa-elmélet, melyben a racionális test körosztási bővítése helyett más, nemkommutatív Galois-csoportú bővítéseit használják.
-függvénye jön elő – ezeknek alapvetően fontos alkalmazásai vannak a Birch–Swinnerton-Dyer sejtés ismert eseteinek bizonyításában. Az elmélet új, manapság is folyamatosan fejlődő ága a nemkommutatív Iwasawa-elmélet, melyben a racionális test körosztási bővítése helyett más, nemkommutatív Galois-csoportú bővítéseit használják.
Lábjegyzetek
1 Sophie Germain a matematika romantikus korszakának izgalmas alakja, autodidakta matematikus, aki férfi néven végezte az egyetemet. (Nők ekkor még nem járhattak egyetemre, az emberi és polgári jogok nyilatkozata, valójában a férfiak és polgárok jogainak nyilatkozata volt (Déclaration des droits de l'homme et du citoyen).)
2 Lame mindezek mellett kiváló matematikus volt, és egyike azon 72 tudósnak akinek nevét megörökítették az Eiffel tornyon.
3 K. L. Jensen eredménye 1915-ből.
4 Lsd.: V. S. Vladimirov: ![]() -adic Analysis and Mathematical Physics World Scientific, Singapore, 1994.
-adic Analysis and Mathematical Physics World Scientific, Singapore, 1994.
5 A számológépek megjelenése előtt a kilenccel adott maradékok megegyezése könnyen kivitelezhető teszt volt az egyszerű számítási hibák kiküszöbölésére.
6 Ez a ![]() darab kiterjesztés olyasmi, mint a komplex test fölött a négyzetgyökfüggvény két ága. Valójában van még egy
darab kiterjesztés olyasmi, mint a komplex test fölött a négyzetgyökfüggvény két ága. Valójában van még egy ![]() -edik ága is a
-edik ága is a ![]() -adikus
-adikus ![]() -függvénynek, ami a 0 modulo
-függvénynek, ami a 0 modulo ![]() maradékhoz tartozik, de ahhoz kicsit erősebb kongruenciákkal kell dolgozni, és ennek az ágnak pólusa lesz az
maradékhoz tartozik, de ahhoz kicsit erősebb kongruenciákkal kell dolgozni, és ennek az ágnak pólusa lesz az ![]() -ban.
-ban.
Tóth Árpád és Zábrádi Gergely
ELTE TTK Matematikai Intézet;
MTA Rényi Alfréd Matematikai Kutatóintézet