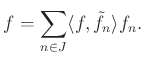A frém (angolul: frame, és a matematikai zsargonban magyarul is a frém szó terjedt el) Hilbert-térbeli vektoroknak egy olyan halmaza, amelynek segítségével más vektorok kifejtését adhatjuk meg, hasonlóan egy bázis szerinti kifejtéshez, noha a frém általában redundáns vagy túltelített. Véges dimenzióban egy frém nem más, mint egy generáló vektorrendszer, de ez az állítás nagyrészt elkendőzi mind a frémek számos gyakorlati alkalmazását, mind pedig a velük kapcsolatban felmerülő mély és megoldatlan matematikai problémákat. Végtelen dimenzióban sok árnyalata van a „generáló” és a „független” szavaknak, és a legfontosabb frémek némelyike túltelített, noha bármely véges részrendszere lineárisan független vektorokból áll. Itt nincs helyünk az alkalmazások részletes tárgyalására, de fontos tudni, hogy ezek keltették fel a frémekkel kapcsolatos érdeklődést. Egy rövid és nem teljes lista az alkalmazásokról a következő: analóg-digitális jelátalakítás, Sigma—Delta-kvantálás, jelrekonstrukció, és nagy adathalmazok elemzése.
A frém fogalmát Duffin és Schaeffer vezették be 1952-ben a Transaction of the AMS-ben megjelent cikkükben. Ebben a cikkben (amely a tiszta érvelés mintapéldánya, és amelyet a mai napig érdemes elolvasni), egy ![]() Hilbert térbeli
Hilbert térbeli ![]() vektorrendszert (ahol
vektorrendszert (ahol ![]() megszámlálható indexhalmaz) frémnek definiáltak, ha léteznek olyan
megszámlálható indexhalmaz) frémnek definiáltak, ha léteznek olyan ![]() konstansok, amelyekre
konstansok, amelyekre
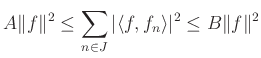
teljesül minden ![]() -ra.
-ra.
Sajnálatos módon Duffin és Schaeffer már nincsenek közöttünk, és senki sem kérdezte meg őket, hogy miért a frém elnevezést vezették be. Vajon azért, mert ![]() és
és ![]() két oldalról korlátozzák a középen álló összeget? (Az angol frame szó korlátot is jelent; megjegyzem aligha ez az elnevezés valódi magyarázata — a ford.) Ezt már sohasem tudjuk meg. Akárhogyan is, egy frémet feszesnek nevezünk, ha
két oldalról korlátozzák a középen álló összeget? (Az angol frame szó korlátot is jelent; megjegyzem aligha ez az elnevezés valódi magyarázata — a ford.) Ezt már sohasem tudjuk meg. Akárhogyan is, egy frémet feszesnek nevezünk, ha ![]() , és Parseval-frémnek, ha
, és Parseval-frémnek, ha ![]() .
.
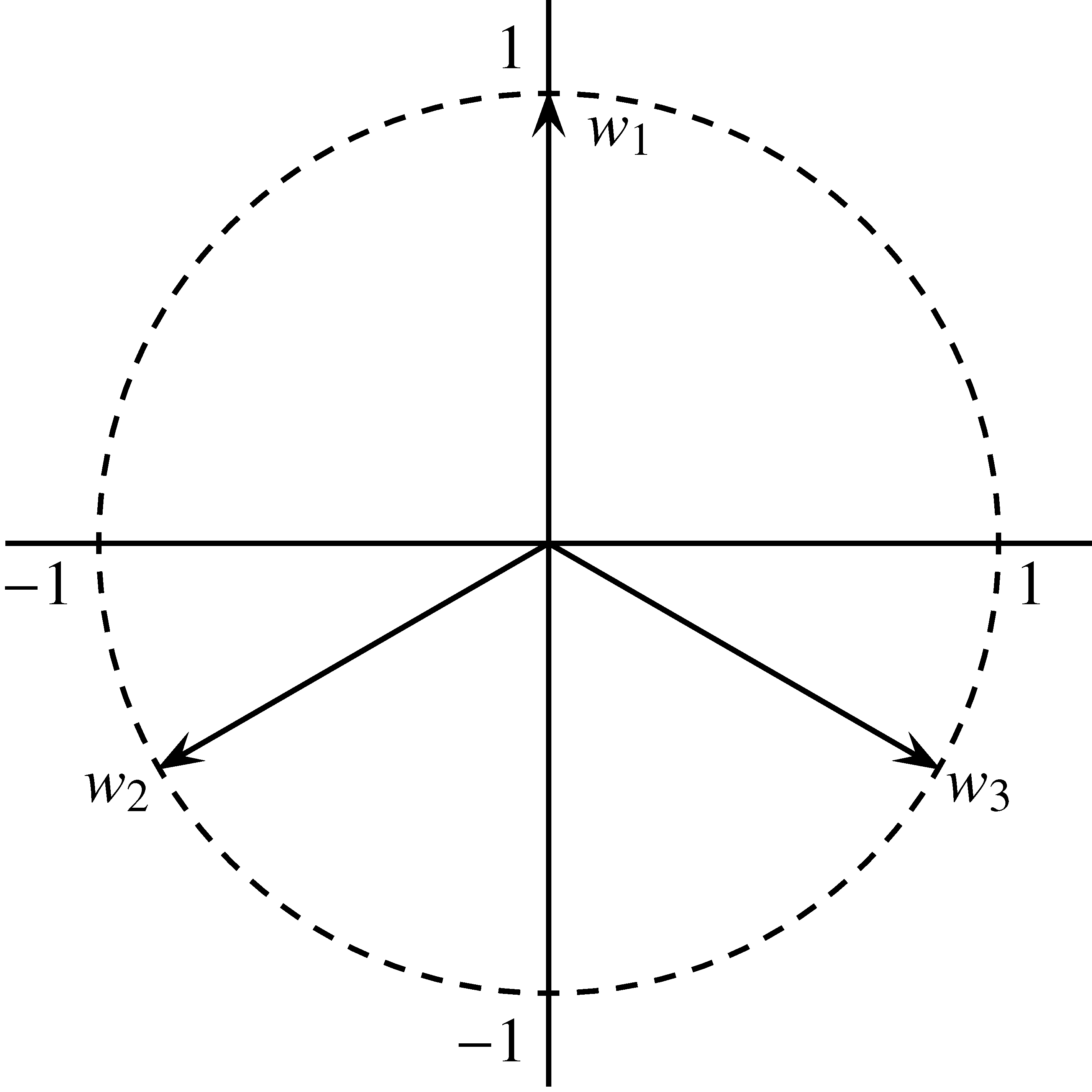
1. ábra. A Mercedes-frém.
Minden ortonormált bázis egyben Parseval-frém is, de egy Parseval-frém nem feltétlenül ortogonális vagy akárcsak bázis. A Mercedes-frém a síkon (1. ábra, ![]() ) egyszerű példát szolgáltat egy feszes frémre (ahol
) egyszerű példát szolgáltat egy feszes frémre (ahol ![]() ). Ha átskálázzuk,
). Ha átskálázzuk, ![]() ,
, ![]() , akkor egy
, akkor egy ![]() -beli Parseval frémhez jutunk. Ekkor minden
-beli Parseval frémhez jutunk. Ekkor minden ![]() esetén
esetén
Az együtthatók egy ilyen kifejtésben nem egyértelműek, hiszen ![]() lineárisan összefüggnek, de ez még előnyös is lehet számos szituációban. Véges dimenzióban gyakran sokkal nagyobb vektorrendszerből álló frémet keresünk egy magas dimenziós térben: például létezik-e 97 darab egységvektor
lineárisan összefüggnek, de ez még előnyös is lehet számos szituációban. Véges dimenzióban gyakran sokkal nagyobb vektorrendszerből álló frémet keresünk egy magas dimenziós térben: például létezik-e 97 darab egységvektor ![]() -ban, amely feszes frémet alkot? Ehhez egyenletesen eloszló pontrendszert kéne találni a 43-dimenziós gömb felszínén, ahol az egyenletesség azonban nem egészen a szokványos értelemben értendő. Egységvektorokból álló feszes frémeket
-ban, amely feszes frémet alkot? Ehhez egyenletesen eloszló pontrendszert kéne találni a 43-dimenziós gömb felszínén, ahol az egyenletesség azonban nem egészen a szokványos értelemben értendő. Egységvektorokból álló feszes frémeket ![]() -ben és
-ben és ![]() -ben FUNTF-oknak hívunk (az angol szavak rövidítése nyomán). Benedetto és Fickus a FUNTF-okat egy bizonyos potenciálhoz tartozó energiafüggvény minimumaként karakterizálta. Ma is aktív kutatási téma olyan FUNTF-ok keresése, amelyben a vektorok azonos szögeket zárnak be, vagy legalábbis közel azonos szögeket. Az ilyen frémek hasznosak lennének például a jelfeldolgozásban.
-ben FUNTF-oknak hívunk (az angol szavak rövidítése nyomán). Benedetto és Fickus a FUNTF-okat egy bizonyos potenciálhoz tartozó energiafüggvény minimumaként karakterizálta. Ma is aktív kutatási téma olyan FUNTF-ok keresése, amelyben a vektorok azonos szögeket zárnak be, vagy legalábbis közel azonos szögeket. Az ilyen frémek hasznosak lennének például a jelfeldolgozásban.
Ha ![]() frém egy
frém egy ![]() Hilbert térben, akkor
Hilbert térben, akkor ![]() egy
egy ![]() -t önmagára képező folytonos lineáris bijekciót definiál. Az
-t önmagára képező folytonos lineáris bijekciót definiál. Az ![]() -hez tartozó duális frém a következő:
-hez tartozó duális frém a következő: ![]() ,
, ![]() . Ekkor minden
. Ekkor minden ![]() -ra teljesül, hogy
-ra teljesül, hogy
Ha a frém feszes, akkor ![]() . Általában az
. Általában az ![]() együtthatók nem az egyetlenek, amelyekre
együtthatók nem az egyetlenek, amelyekre ![]() teljesül, de az (1) egyenlet hasznos stabilitási tulajdonságokkal rendelkezik. Egyrészt, a fenti sor feltétlenül konvergens, azaz bármely átrendezése konvergens. Másrészt, az
teljesül, de az (1) egyenlet hasznos stabilitási tulajdonságokkal rendelkezik. Egyrészt, a fenti sor feltétlenül konvergens, azaz bármely átrendezése konvergens. Másrészt, az ![]() -hez tartozó lehetséges
-hez tartozó lehetséges ![]() együttható sorozatok közül a fenti
együttható sorozatok közül a fenti ![]() -nek van a legkisebb
-nek van a legkisebb ![]() normája (noha gyakran az alkalmazásokban a legkisebb
normája (noha gyakran az alkalmazásokban a legkisebb ![]() normájú együttható-sorozatot keressük). Az (1) szerinti előállítás akkor és csak akkor egyértelmű, ha
normájú együttható-sorozatot keressük). Az (1) szerinti előállítás akkor és csak akkor egyértelmű, ha ![]() egy Riesz-bázis, azaz egy ortonormált bázis folytonos lineáris bijekció általi képe. Egy Riesz-bázisnak semmilyen részhalmaza nem alkothat frémet, de ha egy frém nem Riesz-bázis, akkor biztosan van olyan valódi részhalmaza, amely szintén frém.
egy Riesz-bázis, azaz egy ortonormált bázis folytonos lineáris bijekció általi képe. Egy Riesz-bázisnak semmilyen részhalmaza nem alkothat frémet, de ha egy frém nem Riesz-bázis, akkor biztosan van olyan valódi részhalmaza, amely szintén frém.
Miért van szükségünk olyan frémekre, amelyek nem ortonormált bázisok vagy legalábbis Riesz-bázisok? A klasszikus mintavételi tétel (más néven a Nyquist—Shannon sampling theorem) az információelmélet és jelfeldolgozás egyik alapköve. A mintavételi tétel azzal ekvivalens, hogy az ![]() sorozat feszes frémet alkot
sorozat feszes frémet alkot ![]() -ben minden
-ben minden ![]() esetén. Ha
esetén. Ha ![]() , akkor ortonormált bázist kapunk. Azonban ha
, akkor ortonormált bázist kapunk. Azonban ha ![]() , akkor
, akkor ![]() nem alkot Riesz bázist
nem alkot Riesz bázist ![]() -ben, így a frém szerinti kifejtésben az együtthatók nem egyértelműek (noha
-ben, így a frém szerinti kifejtésben az együtthatók nem egyértelműek (noha ![]() minden véges részrendszere lineárisan független). Ha
minden véges részrendszere lineárisan független). Ha ![]() akkor
akkor ![]()
![]() darab ortonormált bázis uniója, de általában
darab ortonormált bázis uniója, de általában ![]() nem írható fel ortonormált bázisok uniójaként. A mintavételezési tétel van a sávkorlátozott jelek digitális kódolása mögött:
nem írható fel ortonormált bázisok uniójaként. A mintavételezési tétel van a sávkorlátozott jelek digitális kódolása mögött: ![]() szükséges ahhoz, hogy reményünk legyen rekonstruálni az eredeti jelet a digitális kódból.
szükséges ahhoz, hogy reményünk legyen rekonstruálni az eredeti jelet a digitális kódból. ![]() felel meg a „túlmintavételezésnek”, avagy annak, amikor a frém, amit használunk, nem Riesz-bázis. A „8-szorosan túlmintavételezett” felirat a CD-ken ezzel áll szoros kapcsolatban. A túlmintavételezés segít a zajok kiszűrésében és a hibajavításban is.
felel meg a „túlmintavételezésnek”, avagy annak, amikor a frém, amit használunk, nem Riesz-bázis. A „8-szorosan túlmintavételezett” felirat a CD-ken ezzel áll szoros kapcsolatban. A túlmintavételezés segít a zajok kiszűrésében és a hibajavításban is.
Sok egyszerűnek hangzó kérdés frémekkel kapcsolatban mély matematikai problémákhoz vezet. Például, természetes megkérdezni, hogy karakterizálni tudjuk-e a redundancia fogalmát, elsősorban végtelen frémek esetén. Általában egy frém nem írható fel ortonormált bázisok uniójaként, de vajon felírható-e minden ![]() frém nemredundáns
frém nemredundáns ![]() részrendszerek uniójaként? Ezt úgy értjük, hogy egy
részrendszerek uniójaként? Ezt úgy értjük, hogy egy ![]() részrendszer nemredundáns, ha Riesz-bázist alkot az általa kifeszített altér lezártjában. Egy ilyen részhalmazt Riesz-sorozatnak is hívunk. (Véges dimenzióban ez egyszerűen a lineáris függetlenségnek felel meg.) Eltekintve a triviális
részrendszer nemredundáns, ha Riesz-bázist alkot az általa kifeszített altér lezártjában. Egy ilyen részhalmazt Riesz-sorozatnak is hívunk. (Véges dimenzióban ez egyszerűen a lineáris függetlenségnek felel meg.) Eltekintve a triviális ![]() esettől természetesnek látszik a következő sejtés:
esettől természetesnek látszik a következő sejtés:
Feichtinger-sejtés. Ha ![]() frém a
frém a ![]() Hilbert térben és
Hilbert térben és ![]() , akkor léteznek olyan
, akkor léteznek olyan ![]() Riesz-sorozatok, amelyeknek uniója
Riesz-sorozatok, amelyeknek uniója ![]() .
.
Casazza és Tremain megmutatták, hogy a Feichtinger-sejtés ekvivalens a Kadison—Singer-sejtéssel avagy a „kirakási” sejtéssel (Paving conjecture), amelyet az operátorelmélet egyik legmélyebb nyitott kérdésének tartottak (azóta már sikerült megtalálni a megoldást, lásd pl. The Solution of the Kadison—Singer Problem https://arxiv.org/abs/1712.08874 — a ford.).
Kirakási sejtés (Paving conjecture): Minden ![]() -hoz létezik olyan
-hoz létezik olyan ![]() , hogy minden
, hogy minden ![]() -re és minden
-re és minden ![]() -es 0 főátlójú
-es 0 főátlójú ![]() mátrixra létezik egy olyan
mátrixra létezik egy olyan ![]() partíciója az
partíciója az ![]() halmaznak, amelyre
halmaznak, amelyre
ahol ![]() a
a ![]() altérre való ortogonális projekciót jelöli, és
altérre való ortogonális projekciót jelöli, és ![]() az operátornorma.
az operátornorma.
Duffint és Schaeffert különösen érdekelték az ![]() alakú frémek
alakú frémek ![]() -ben, ahol
-ben, ahol ![]() tetszőleges valós vagy komplex sorozat. Az ilyen nemharmonikus Fourier-frémek nemegyenletes mintavételi tételeket adnak sávkorlátozott jelek esetében. És noha a frémek elmélete Duffin és Schaeffer után még sok évig nem került reflektorfénybe, a nemegyenletes mintavétel manapság egy nagyon fontos terület mind a sávkorlátozott mind a nem-sávkorlátozott jelek feldolgozásában; felmerül például a mágneses rezonancia vizsgálat (MRI) során is.
tetszőleges valós vagy komplex sorozat. Az ilyen nemharmonikus Fourier-frémek nemegyenletes mintavételi tételeket adnak sávkorlátozott jelek esetében. És noha a frémek elmélete Duffin és Schaeffer után még sok évig nem került reflektorfénybe, a nemegyenletes mintavétel manapság egy nagyon fontos terület mind a sávkorlátozott mind a nem-sávkorlátozott jelek feldolgozásában; felmerül például a mágneses rezonancia vizsgálat (MRI) során is.
1986-ban Daubechies, Grossmann és Meyer újra a frémekre irányították a figyelmet az ![]() -beli Gábor-frémekkel és wavelet frémekkel kapcsolatos munkájukkal. Egy (rácsos) Gábor-frém a következő formájú:
-beli Gábor-frémekkel és wavelet frémekkel kapcsolatos munkájukkal. Egy (rácsos) Gábor-frém a következő formájú: ![]() , ahol
, ahol ![]() és
és ![]() (természetesen a
(természetesen a ![]() paramétreket megfelelően kell választani, hogy ténylegesen frémet kapjunk ilyen módon). Tehát egy Gábor-frémet úgy kapunk hogy egyetlen
paramétreket megfelelően kell választani, hogy ténylegesen frémet kapjunk ilyen módon). Tehát egy Gábor-frémet úgy kapunk hogy egyetlen ![]() függvényre alkalmazzuk eltolásoknak és modulációknak egy diszkrét halmazát. Emiatt ezek a frémek kapcsolódnak a reprezentáció-elmélethez, a Heisenberg csoporthoz és a határozatlansági elvhez is. Például a Balian—Low tétel azt mondja, hogy ha egy Gábor-frém egyúttal Riesz-bázisa is
függvényre alkalmazzuk eltolásoknak és modulációknak egy diszkrét halmazát. Emiatt ezek a frémek kapcsolódnak a reprezentáció-elmélethez, a Heisenberg csoporthoz és a határozatlansági elvhez is. Például a Balian—Low tétel azt mondja, hogy ha egy Gábor-frém egyúttal Riesz-bázisa is ![]() -nek, akkor a
-nek, akkor a ![]() Heisenberg-féle szorzat mindenképpen végtelen. Ezért az ilyen Gábor-frémek kevésbé hasznosak. Másfelől viszont Feichtinger és Gröchenig megmutatták, hogy ha
Heisenberg-féle szorzat mindenképpen végtelen. Ezért az ilyen Gábor-frémek kevésbé hasznosak. Másfelől viszont Feichtinger és Gröchenig megmutatták, hogy ha ![]() Gábor-frémet alkot
Gábor-frémet alkot ![]() -ben, akkor ez a frém stabil bázis-szerű kifejtést biztosít nem csak négyzetesen integrálható függvényekre, hanem bármely
-ben, akkor ez a frém stabil bázis-szerű kifejtést biztosít nem csak négyzetesen integrálható függvényekre, hanem bármely ![]() modulációs térben lévő függvényre is. Így aztán az egyszerű Hilbert-térbeli frém feltétel automatikusan maga után von sokkal általánosabb kifejtési tételeket egyéb függvényterekben. Hasonló kifejtési tételek érvényesek „irreguláris” Gábor-frémek esetében, azaz
modulációs térben lévő függvényre is. Így aztán az egyszerű Hilbert-térbeli frém feltétel automatikusan maga után von sokkal általánosabb kifejtési tételeket egyéb függvényterekben. Hasonló kifejtési tételek érvényesek „irreguláris” Gábor-frémek esetében, azaz ![]() alakú frémekre, noha a bizonyítások sokkal bonyolultabbak. A legújabb ilyen irányú eredmények a Wiener-lemma nemkommutatív Banach-algebrákra vonatkozó verzióját használják.
alakú frémekre, noha a bizonyítások sokkal bonyolultabbak. A legújabb ilyen irányú eredmények a Wiener-lemma nemkommutatív Banach-algebrákra vonatkozó verzióját használják.
Egy wavelet frémet eltolásokkal és skálázásokkal kapunk. Nevezetesen, ha ![]() és
és ![]() , és
, és ![]() frémet alkot, akkor azt wavelet frémnek nevezzük. A Gábor-frémekkel ellentétben itt lehet találni olyan szép
frémet alkot, akkor azt wavelet frémnek nevezzük. A Gábor-frémekkel ellentétben itt lehet találni olyan szép ![]() függvényeket, amelyekre
függvényeket, amelyekre ![]() Riesz-bázis
Riesz-bázis ![]() -ben, sőt olyanokat is, amelykre ortonormált bázis. Meyer, Mallat, Daubechies ezen észrevétele volt a „wavelet forradalom” kezdete. Egy „viszonylag szép”
-ben, sőt olyanokat is, amelykre ortonormált bázis. Meyer, Mallat, Daubechies ezen észrevétele volt a „wavelet forradalom” kezdete. Egy „viszonylag szép” ![]() függvény által generált wavelet frém vagy ortonormált bázis szerint nemcsak
függvény által generált wavelet frém vagy ortonormált bázis szerint nemcsak ![]() -beli függvények kifejtéseit adhatjuk meg, hanem egy sor fontos Banach-térbeli függvényét is, beleértve Sobolev-tereket, Besov-tereket és Triebel—Lizorkin-tereket. A wavelet frémeknek fontos alkalmazásai vannak napjainkban, csakúgy mint az egyéb általánosításaiknak, amelyeket video- és képfeldolgozásban hasznosítanak. A frémeknél is jobban túltelített rendszerek pedig a tömörített érzékelés (compressed sensing) és a ritka reprezentációk (sparse representation) alapjait adják.
-beli függvények kifejtéseit adhatjuk meg, hanem egy sor fontos Banach-térbeli függvényét is, beleértve Sobolev-tereket, Besov-tereket és Triebel—Lizorkin-tereket. A wavelet frémeknek fontos alkalmazásai vannak napjainkban, csakúgy mint az egyéb általánosításaiknak, amelyeket video- és képfeldolgozásban hasznosítanak. A frémeknél is jobban túltelített rendszerek pedig a tömörített érzékelés (compressed sensing) és a ritka reprezentációk (sparse representation) alapjait adják.
Végül megemlítünk még egy nyitott problémát. Nem nehéz belátni, hogy a Duffin és Schaeffer által tanulmányozott nemharmonikus ![]() rendszer bármely véges részhalmaza lineárisan független. A
rendszer bármely véges részhalmaza lineárisan független. A ![]() rácsos Gábor-rendszerekre szintén teljesül ez a tulajdonság, még akkor is ha nem alkotnak frémet. Nem ismert azonban ez a tulajdonság irreguláris Gábor-rendszerekre. Ezen írás megszületése idején a következő sejtés továbbra is nyitott (amennyire tudom, azóta is — a ford.):
rácsos Gábor-rendszerekre szintén teljesül ez a tulajdonság, még akkor is ha nem alkotnak frémet. Nem ismert azonban ez a tulajdonság irreguláris Gábor-rendszerekre. Ezen írás megszületése idején a következő sejtés továbbra is nyitott (amennyire tudom, azóta is — a ford.):
Idő- és frekvenciaeltolások lineáris függetlenségi sejtése: Ha ![]() nem azonosan nulla, és
nem azonosan nulla, és ![]() valós számpárok véges halmaza, akkor a
valós számpárok véges halmaza, akkor a ![]() függvények lineárisan függetlenek.
függvények lineárisan függetlenek.
Ezt a sejtést HRT-sejtés néven is ismerik. Sok speciális esete már bizonyított, de teljes általánosságban továbbra is nyitott. Ismert például ![]() esetén, de nyitott
esetén, de nyitott ![]() -re még akkor is ha feltesszük, hogy
-re még akkor is ha feltesszük, hogy ![]() végtelenszer differenciálható. Sőt, még az alábbi az alábbi sejtés is nyitott:
végtelenszer differenciálható. Sőt, még az alábbi az alábbi sejtés is nyitott:
HRT-részsejtés: Ha ![]() nem azonosan nulla, és végtelenszer differenciálható, akkor
nem azonosan nulla, és végtelenszer differenciálható, akkor ![]() lineárisan független halmaz.
lineárisan független halmaz.
Christopher Heil
Irodalomjegyzék
[CK13] P. G. Casazza and G. Kutyniok, eds., Finite Frames, Birkhäuser/Springer, New York, 2013.
[Chr03] O. Christensen, An Introduction to Frames and Riesz Bases, Birkhäuser, Boston, 2003.
[Heil11] C. Heil, A Basis Theory Primer, Expanded Edition, Birkhäuser, Boston, 2011.
[You01] R. Young, An Introduction to Nonharmonic Fourier Series, Revised First Edition, Academic Press, San Diego, 2001.
Christopher Heil a Georgia Institute of Technology matematikaprofesszora. E-mailcíme: Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.. DOI: http://dx.doi.org/10.1090/noti1011. A cikk eredetileg a Notices of the American Mathematical Society folyóiratban 2013-ban jelent meg a What is... rovatban. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. A fordítást készítette: Matolcsi Máté.
Christopher Heil, “What is...a Frame?” Noces Amer. Math. Soc., 60, No. 6 (June/July 2013) 748-750. ©2013 American Mathemacal Society.
Fotó: https://www.pexels.com/photo/abstract-art-artistic-design-310446/