Farkas Gyula nyomában: Szemelvények egy természettudós életéből és tudományos hatásából

170 évvel ezelőtt született Farkas Gyula fizikus, matematikus. Farkas Gyula életének jelentősebb eseményei — ma már — ismertek a magyar tudományos közélet előtt.¹ Megemlékezésünkben két kérdéssel foglalkozunk: a Farkas-lemma hatásával és Farkas Gyula életének, néhány — nem mindenki számára ismert — részletével, amelyek egyszerre mutatják be Farkas Gyulát, az embert és a tudóst.

1. „...eszméinek diadala...”

A tények azt mondják, hogy a magyar matematikusok közül Farkas Gyula lineáris egyenlőtlenséggel kapcsolatos eredményei mára az egyik legidézettebbek! Elevenítsük fel a híressé vált matematikai eredményt Farkas Gyula dolgozatának² egy részletével, amelyet a Magyar Tudományos Akadémia III. Osztályának 1898. október 17-én megtartott ülésén ismertetett.

„...Legyen

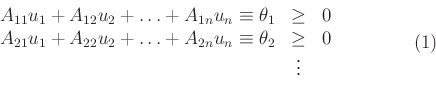
$\begin{displaymath} \begin{array}{rcl} A_{11}u_{1}+A_{12} u_{2}+\ldots+A_{1n} u_... ...iv \theta_{2}&\ge& 0\\ &\vdots&\\ \end{array}\qquad\qquad(1) \end{displaymath}$

egyenlőtlenségi rendszerünk (1), és ennek minden megoldásában teljesüljön

$\displaystyle A_{1}u_{1}+A_{2}u_{2}+\ldots+A_{n}u_{n}\equiv\upsilon\ge 0.\qquad\qquad(2)$

A Fourier-féle mechanikai elv alkalmazásának algebrai alapját a következő tantétel képezi: mindig léteznek olyan nem negatív, az $u$ vezérmennyiségektől független multiplicatorok $\lambda$ , hogy

$\displaystyle \upsilon\equiv \lambda_{1}\theta_{1}+\lambda_{2} \theta_{2}+\ldots\qquad\qquad(3)$

...”

Farkas jelölését megtartottuk, így talán egy kis magyarázatra szorul a mai olvasó számára. Legegyszerűbb az, ha kimondjuk a szövegben található definíciót és állítását a matematika mai jelölésrendszerét használva.

Definíció. Legyen adott egy $A$ $m\times n$ -es valós mátrix és egy $n$ elemű valós $c$ (oszlop)vektor. Tekintsük az

$\displaystyle Au\ge 0\qquad\qquad(4)$

homogén lineáris egyenlőtlenség-rendszert, ahol $u$ a változók egy $n$ -dimenziós vektora. A

$\displaystyle c^{\top}u\ge 0\qquad\qquad(5)$

lineáris egyenlőtlenség következménye a (4) rendszernek, ha (4) tetszőleges megoldása egyben (5) megoldása is.

A Farkas-lemmát, a mai matematikai nyelvezetet használva, abban a — kicsit általánosabb — formában mondjuk ki, ahogyan azt első — e témakörben megjelent — közleményében, 1894-ben³ maga Farkas Gyula is megfogalmazta.

Lemma. Legyen adott egy $A$ $m\times n$ -es valós mátrix és egy $n$ elemű valós $c$ (oszlop) vektor. Tekintsük a (4) homogén lineáris egyenlőtlenség-rendszert, ahol $u$ a változók egy $n$ -dimenziós vektora. Az (5) lineáris egyenlőtlenség pontosan akkor következménye a (4) homogén lineáris egyenlőtlenség-rendszernek, ha létezik $m$ -dimenziós, nem negatív $v$ vektor, amelyre a

$\displaystyle v^{\top}A=c^{\top}\qquad\qquad(6)$

lineáris egyenletrendszer teljesül.

Most már csak egy apró lépés van hátra, ahhoz, hogy a Farkas-lemmát olyan formában (alternatíva tétel) fogalmazzuk meg, ahogyan azt ma ismerjük és használjuk.

Farkas-lemma. Legyen adott egy $A$ $m\times n$ -es valós mátrix és egy $n$ elemű valós $c$ (oszlop)vektor. Ekkor a következő két lineáris egyenlőtlenségrendszer közül pontosan az egyiknek van megoldása

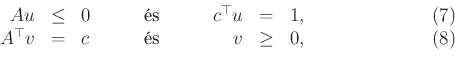
$\begin{displaymath}\begin{array}{rclcrclr} A u&\le&0&\qquad\text{és}\qquad\qqua... ...ext{és}\qquad\qquad&v&\ge&0,&\qquad\qquad\qquad(8) \end{array}\end{displaymath}$

ahol az $u$ egy $n$ -dimenziós, míg a $v$ egy $m$ -dimenziós vektor.

Belátható, hogy a Farkas-lemma két különböző változata ekvivalens, és a második változat — kisebb adatmegadási eltérésektől eltekintve — az, amilyen formában az elmúlt közel 70 évben (leggyakrabban) hivatkozták.

Farkas Gyula, szerencsére, eredményeit több német nyelvű cikkben is közölte, amelyek közül az 1901-es cikk ⁴ a legismertebb.

Bármennyire is furcsa, de Farkas Gyula alapvető eredményének nagyobb idézettsége van, mint a Bolyai-geometriának, vagy Riesz Frigyes, Fejér Lipót, Erdős Pál, Rényi Alfréd eredményeinek.

Farkas német nyelvű közléseire a hivatkozások a Google Scholar ⁵szerint meghaladják a 600-at. Ami még érdekesebb, hogy a Farkas-lemma közvetett hivatkozásai pedig a Google Scholar szerint több, mint 70 ezerre tehetők.

Természetesen ez nem azt jelenti, hogy ő lenne a legismertebb magyar matematikus, hiszen Erdős Pál sokkal ismertebb, de egyelőre — úgy tűnik, hogy — Farkas Gyula vezet az idézett magyar matematikai eredmények nem hivatalos listáján. Természetesen minden relatív, akár csak a sportban. Akinek ma van a legtöbb pontja, annak holnap már nincs, és ez a tudományban is így van!

A fentebb felsorolt nagy magyar matematikus nevek mellett talán éppen Farkas Gyula a legkevésbé ismert a közvélemény előtt! Először is azért, mert ő magát elméleti fizikusnak vallotta, és a matematikai eredményei is a fizikai meglátásainak bizonyítására kellettek.

De a Sors is nagyon érdekesen rendezte életét. Noha a mai csonka Magyarországon született egy pusztán, tevékenységét a kolozsvári Ferenc József Tudományegyetemen fejtette ki, ahol az elméleti fizika professzora volt. 1914-után újra Budapestre költözött és Pestszentlőrincen hunyt el. Ott is temették el. Az 1970-es években még Filep László (nyíregyházi matematikatörténész) és Prékopa András (matematikaprofesszor, az MTA rendes tagja) felkereste, és helyrehozatta a sírját, de azt később egy áruház építése miatt felszámolták. Így ma már nincs meg a sírja!⁶

Az igazsághoz tartozik, hogy halála után még néhány évig a kortársai emlékeztek rá, de azután teljesen megfeledkeztek róla. Egészen 1951-ig, amikor is az amerikaiak felfedezték! Egészen pontosan Oláh-Gál Róbertnek így mesélte Prékopa András professzor Farkas Gyula felfedezését: Kuhn és Tucker egy monográfiát készültek írni a lineáris programozásról. Ekkor elküldték egyik PhD hallgatójukat, nézzen utána az egyetem könyvtárában, hogy kik is írtak addig a lineáris egyenlőtlenségekről. Így fedezték fel Farkas Gyula német nyelvű cikkét, amely a Crelle Journalban jelent meg 1901-ben. Kuhn és Tucker ezek után szisztematikusan megkeresték Farkas Gyula német nyelvű cikkeit. A nemlineáris (konvex) programozási feladat szükséges és elégséges optimalitási kritériumát ⁷ a Farkas-lemma segítségével igazolták, és Farkas Gyula 1901-es német nyelvű dolgozatára hivatkoztak. Kuhn és Tucker cikkének megjelenése után lett ismert a tudós világban az ún. Farkas-lemma.

Farkas Gyula lemmája a lineáris egyenlőtlenségrendszerek megoldhatóságával foglalkozik. Meglepő módon kevésbé ismert, hogy a lineáris egyenletrendszerek megoldhatóságát is vizsgálhatjuk alternatíva tételek segítségével. Ezek közül a legismertebb az un. Rouché—Kronecker—Capelli-lemma⁸. A Rouché—Kronecker—Capelli, illetve a Farkas-lemmák legegyszerűbb ismert bizonyítását Klafszky és Terlaky adták meg 1989-ben. Úgy gondoljuk, hogy ezek a bizonyítások már középiskolában — matematika szakkörön — elmondhatók a lineáris egyenletrendszer tárgyalása után.

2. Farkas Gyula és a Bolyaiak

Itt tennénk egy kis kitérőt. A Bolyaiak neve is azután lett ismert a világban, hogy Gauss halála (1855) után kiadták Gauss levelezését. Ebben Gauss azt írja, hogy csak a Bolyaiak értették meg metafizikai eszmefuttatásait. Ez késztette aztán arra a matematikus társadalmat, hogy utánanézzenek, kik is voltak a Bolyaiak! Ez azért érdekes, mert Farkas Gyula képviselte az MTA-t Marosvásárhelyen 1911. július 30-án a két Bolyai exhumálásán, ahol egy nagyon találó beszédet mondott:

„Bolyaiak! Mélységekben fürkésző apa és messzeségekbe ellátó fia! A Magyar Tudományos Akadémia nevében köszöntöm hamvaitokat. Íme, gondos intézkedés porotok egymáshoz térítette, mert hiába lett rajtatok is meghasonlás áldatlan foganatja: együvé tartoztok nemcsak a természet anyagbeli rendje szerint, hanem azon rendje szerint is, a mely a szellemi élet országait kormányozza végtelen időkig.

Mióta pedig az örök békesség honába költöztetek, azóta ,az arithmetica és geometria együtt gyökeredző s koronájukkal összefolyó fája' dúsan termett, s termésében megérlelte a ti eszméiteket is és az ,Appendix, Scientiam Spatii absolute veram exhibens' nagy dicsőséghez jutott, és ma hatalmas természeti törvény is magához emeli azt, törvények törvénye, gondolkodásunkat oly téridő-világban szólító, a melyben a térnek Bolyai-világa új lendületre kap. Dicsőségtek fényében a Föld egész kerekségére szóló emléket állított Akadémiánk a Bolyai-alapítványban tinéktek, kik által a magyar állameszme fogalma oszlopos alkotó elemmel lett gazdagabb.

Fájdalom, a tudomány amaz építő mesterinek a sorába kerültetek, akik nem érhetik meg eszméik diadalát. De ennek az emberi gyarlóságra nehezedő keserűsége elenyésző kicsinység annak a jutalomnak a mekkoraságához képest, a mely a megismerés fő-főmunkásait magában a megismerésben jutalmazza meg. Azért nem is fáj annyira, hogy csak mi távoli utódok hallathatjuk művetekben a méltó megbecsülés és hála igéit.

Ezek adójával teszem le én is drága sírotokra a Magyar Tudományos Akadémia koszorúját.” ⁹

Farkas Gyula fenti szavai prófétaiak lettek, mert az ő munkásságára is tökéletesen ráillik, hogy nem érhette meg eszméinek diadalát, de a tudományos megismerés bőségesen megjutalmazta az utódok kutatásaiban.

Farkas Gyulának életében kapott legnagyobb elismerése az volt, hogy a páduai egyetem díszdoktorává avatta. Ez igen mélyen megérintette őt, bár ez az elismerés valamelyest formális volt, mert az összes Galilei-ünnepségre meghívott külföldi küldöttet díszdoktorrá avatták.

3. „Meghalt Farkas Gyula, a magyar természettudósok nesztora”

Egy érdekes okirattal szeretnénk emlékezni Farkas Gyulára:

Az Est újság 1830. december 30-i száma közölt egy rövid nekrológot. Honnan vettük észre? Fejér Lipót hagyatékában volt a kivágott újságcikk!

„Meghalt Farkas Gyula, a magyar természettudósok nesztora

Az Est tudósítójától

Farkas Gyula, aki a kolozsvári egyetemen tanította az elméleti fizikát egy emberöltőn át, tegnap meghalt. Farkas Gyula működésével dicsőséget szerzett a magyar matematikai és fizikai tudományosságnak. Hetvennél több tudományos értekezése jelent meg és pedig tetemes részük német és francia folyóiratokban, visszhangot keltve a külföldi tudósok munkáiban is.

1847-ben született egy fehérmegyei pusztán. Előbb jogásznak készült és csak később szánta el magát a matematikai stúdiumokra. 1870-től 1874-ig az akkori székesfehérvári alreáliskolában és később a pápai tanítóképzőben tanított.

Életének kialakulására döntő volt, hogy 1874-tői 1880-ig gróf Batthyány Gézánál működött mint nevelő. Növendékeivel sokat utazott külföldön és itt fejlődött ki benne a matematika és a természettan iránti mélységes érdeklődése. Elmélyedt a felsőbb matematikában annyira, hogy önálló dolgozatokat nyújtott be a párizsi akadémiának. Külföldről hazajövet megszerzi az egyetemi magántanárságot, olyan előadásokat hirdetett, aminőkről magyar egyetemi hallgató eladdig sohasem hallhatott. 1887-ben a kolozsvári egyetem tanára lett.

Ő volt az elsők egyike, aki Einstein elméletének jelentőségét felfogta.

Alighogy a relativitásra vonatkozó einsteini dolgozat megjelent, már Farkas Gyula foglalkozott vele, és új szempontokból világította meg az elméletet. Ezzel és az elektromosság és mágnességre vonatkozó dolgozatok egész sorozatával szinte fiatalos lelkesedéssel iparkodott beléhatolni az újabb fizikai elméletekbe. Lelkének ruganyosságát mindvégig megőrizte, bár szemevilágát majdnem teljesen elveszítette és súlyos betegség rágta a szervezetét. Még néhány évvel ezelőtt is Einstein gravitációs nehézségi elméletéről értekezett.

Nemeslelkű, egyszerű, szerény, csak is a tudománynak élő tudós volt. Gyermeteg kedélyét mindvégig megőrizte.

Mindig a legjobbat kereste. A kolozsvári egyetemre minden melléktekintet nélkül a legkiválóbbakat hozta. Így Schlesingert, a bonni egyetem tanárát, Fehér Lipótot, Riesz Frigyest és Haár Alfrédot és ezzel egyetemét európai nívóra emelte. Amikor lemondott tanszékéről, hogy fiatalabb erőnek adja át a helyét, ő választotta ki utódjául a legarravalóbb fiatal tudóst.

Meg kellett érnie, hogy az ő nagyranevelt fakultása elmenekült, de egyben örömmel töltötte el lelkét, hogy megfiatalodva láthatta viszont Szegeden. Kartársai, akik közelebbről ismerték, rajongásig szerették, tanítványai imádták.”

Felvetődik az a logikus kérdés, ki írhatott Farkas Gyula halála napján ilyen szakszerű nekrológot az Est újságban, és miért vágta ki ezt az újságcikket Fejér Lipót. Néhány, a matematika iránt érdeklődő kolléga szerint lehetséges, hogy a megemlékezést maga Fejér Lipót írta, vagy legalábbis szakmai segítséget nyújtott a korabeli tudósítónak, hogy ilyen pontos megemlékezést írjon. Akárhogy is történt, tény, hogy az Est megemlékezése telitalálat volt, mert Farkas Gyulából valóban a magyar természetvizsgálók nesztora lett. Farkas Gyula és Fejér Lipót igen jó barátságban és állandó levelezésben álltak. A Fejér Lipót kézirati hagyatékának igen becses értéke a Farkas Gyulával való levelezés, mely az ELTE Maglódi úti levéltárában olvasható. Ugyancsak ott találtuk meg Farkas Gyula itt bemutatott gyászjelentőjét is. A gyászjelentő azért érdekes és fontos, mert további kutatásra serkentheti a matematikatörténészeket, hogy felkutassák, mi lett a Farkas Gyula örökbefogadott fiával, illetve annak utódaival. A Farkas-Nirnsee-család kézirati hagyatékát keressük. Ez pedig igen fontos kérdésekre adhat választ. Tudjuk azt, hogy Farkas Gyulának levelet írt Minkowski, és tudjuk azt, hogy Haar Alfréd bizonyos értelemben kiegészítette Farkas Gyula lineáris egyenlőtlenségekre vonatkozó kutatásait. De vajon levelezett-e Farkas Gyula Minkowskival, Haar Alfréddal, esetleg Neumann Jánossal stb.? Ezek mára igen izgalmas kérdések volnának. Tehát érdemes volna megtudni, mi lett Farkas Gyula unokájával, Farkas-Nirnsee Egonnal. Egyelőre annyit tudunk róla, hogy a Karády-filmeknél ügyelő volt. ¹⁰ Tehát van esélye annak, hogy a család megőrizte Farkas Gyula kézirati hagyatékát!

Abban is reménykedünk, hogy talán szerény írásunk olvasói közt lesz olyan, aki többet tud a Farkas-Nirnsee-családról és azt szíveskedne nekünk is megírni. Mi mindenesetre megpróbáljuk felkutatni a Farkas Gyula utódait!

Illés Tibor

Differenciálegyenletek Tanszék,

Budapesti Műszaki és Közgazdaságtudományi Egyetem, Budapest

Oláh-Gál Róbert

Gazdaságtudományi Tanszék,

Sapientia Erdélyi Magyar Tudományegyetem, Csíkszereda

Lábjegyzetek

¹: További információk találhatók Prékopa András, Az optimalizálás elmélet kialakulásának történetéről. Alkalmazott Matematika Lapok 4 (1978), 165—191.
Gurka Dezső, Farkas Gyula munkásságának megújuló hatásai. Alkalmazott Matematika Lapok 25 (2008), 137—142.
²: Farkas Gyula: A Fourier-féle mechanikai elv alkalmazásának algebrai alapja. Mathematikai és Természettudományi Értesítő, 16. kötet 361—364. oldalak, Budapest, 1898. (Letölthető az alábbi címről: http://real-j.mtak.hu/4430/1/MatematikaiTermTudErtesito16.pdf)
³: Farkas Gyula: A Fourier-féle mechanikai elv alkalmazásai. Mathematikai és Természettudományi Értesítő, 12. kötet 457-472. oldalak, Budapest, 1894. (Letölthető az alábbi címről http://real-j.mtak.hu/4426/1/MatematikaiTermTudErtesito_12.pdf)
⁴: J. Farkas, Über die Theorie der einfachen Ungleichungen. Journal für die Reine und Angewandte Mathematik, 124:1—27, 1901. (Letölthető az alábbi címről https://eudml.org/doc/149129)
⁵: https://scholar.google.com/scholar?hl=hu&q=J.+Farkas Google Scholar 679 idézetet mutat, de arra a 679 hivatkozóra még van kb. 70-80 ezer hivatkozás. Ezzel szemben az 1894-es első Farkas lineáris egyenlőtlenséges publikációra mindösszesen 61 hivatkozás ismert. Ekkora hátrány a magyar nyelv? (Érdekes, hogy Egerváry 1931-es magyar nyelvű cikkére 162 hivatkozást jegyez a Google Scholar.) A Farkas lemmára, https://www.google.co.uk/search?q=Farkas+lemma&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&ei=s-ayWNj_B87U8gfKiKe4CgFarkas-lemma már 75 200 hivatkozást ad a google!
⁶: Köszönet Kása Zoltán kolozsvári professzornak a fenti információkért! További információk találhatók Gurka Dezső, Farkas Gyula munkásságának megújuló hatásai. Alkalmazott Matematika Lapok 25 (2008), 137—142.
⁷: H. W. Kuhn and A. W. Tucker, Nonlinear Programming. Proceedings of 2nd Berkeley Symposium. Berkeley: University of California Press. pp. 481—492, 1951. (http://projecteuclid.org/euclid.bsmsp/1200500249)
⁸: Klafszky Emil és Terlaky Tamás, A pivot technika szerepe a lineáris algebra néhány alapvető tételének bizonyításában. Alkalmazott Matematikai Lapok 14 (1989) 425—448. (Letölthető az alábbi címről: http://real-j.mtak.hu/453/1/ALKMAT14.pdf)
⁹: Forrás: Farkas Gyula e. t. beszéde Bolyai János hamvainak atyja mellett elhelyezése alkalmával. Marosvásárhelyt, 1911. július 7. = Akadémiai Értesítő 22 (1911) p. 526.
¹⁰: Köszönet Szabó Péter Gábor szegedi matematikatörténész kollégának a közölt információért!

Információk

Főmenü