A gondolkodó embert mindig is foglalkoztatta az a kérdés, hogy az őt körülvevő világ milyen. Ennek leírása pedig csak geometriai fogalmakkal lehetséges, így nem meglepő ezek igen korai feltűnése. Jóval a görög matematika megjelenése előtt, már az egyiptomi matematikában találunk pontos térgeometriai számításokat, természetesen a ma euklideszi geometriának nevezett rendszer szabályai alapján. (A téma iránt érdeklődő olvasó számára ajánlom B. L. van der Waerden remek [17] könyvét.) A világ szerkezetének tudományos leírására való törekvésben az euklideszi geometria hegemóniája addig tartott, amíg a csillagászati méretek és a hatalmas sebességek tekintetében ki nem derült a Newtoni mechanika elégtelensége, és fel nem váltotta azt a fizikai világról alkotott képünk alakításában Einstein relativitáselmélete. Mindez a XX. század kezdetére tehető, természetesen nem minden előzmény nélkül. A XIX. század geometriájában történik egy radikális szemlélet változás, ami alapvetően határozta meg a további tudományos kutatások irányát, Lambert, Gauss és Riemann munkássága a háromdimenziós euklideszi tér felületeinek belső (mai szóhasználattal beágyazástól mentes) geometriájára irányítja a figyelmet, szétválasztva a lokális és globális geometriai tulajdonságokat egymástól; míg Gauss, Bolyai Farkas, Bolyai János és Lobacsevszkij kutatásai nyomán bizonyítást nyer, hogy van minden tekintetben megfelelő globális alternatívája is az euklideszi geometriának. Einstein munkásságával egyidőben alkotja meg Minkowski és Lorentz a téridő matematikai modelljét és alakul ki Minkowski másik geometriája, mely az analízis egyik alapstruktúrájának, a véges dimenziós normált térnek a geometriai tulajdonságait összegzi. Ezekről a geometriákról szeretnénk ebben a cikkben írni, hiszen ezek képezik az alapjait minden további, a világ szerkezetének leírása céljából kidolgozott matematikai struktúrának, a Riemann- és Lorentz-sokaságoknak, vagy a semi-Riemann- és Finsler-tereknek.
Analitikus euklideszi geometria
Az euklideszi geometria megalapozása közel 2000 éven keresztül szintetikus axiómarendszer használatával történt. Az első ilyen tárgyú rendszerezett munka i.e. 300 körül láthatott napvilágot Eukleidész Elemek c. művében (ld. [5]). Descartes nevéhez kapcsolható az első szisztematikus analitikus geometriai számítás, mely alapján kialakul a koordináta-rendszer fogalma és a koordinátánkénti számolás lehetősége. A vektor fogalom kialakulására a XIX. század közepéig kellett várni, habár Gauss és Cauchy már a század elején megalkotják a lineáris egyenletrendszerek elméletét, kidolgozva a determináns elméletet is. Maga a vektor szó W. R. Hamilton nevéhez kapcsolódik, aki ezt először a komplex számok felépítésénél majd a kvaterniók definiálása során használta (ld. [11]). A vektorterek elmélete mégis leginkább H. G. Grassmann 1844-ben megjelent [7] könyvéhez kapcsolható. Az euklideszi geometria modern analitikus tárgyalása így későbbre datálható, a vektorterek elméletének kidolgozása a XIX. század második felében történhetett meg. Ma a lineáris algebra kerek elméletként jelenik meg egy kiforrott, minden egyéb matematikában felbukkanó egységes törzsanyaggal. Ebben a lineáris függetlenség és összefüggőség alaptulajdonságainak vizsgálata után a legfontosabb lineáris leképezésekkel, ezek mátrix reprezentációival és egy szokatlan új művelettel, a skaláris szorzattal ismerkedhetünk meg. A skaláris (vagy belső) szorzás jelenti a hidat az absztrakt algebrai képződmény (a vektortér) és a valóságos geometriai tér között. Skaláris szorzattal rendelkező vektorteret nevezünk euklideszi vektortérnek, azon egyszerű oknál fogva, hogy ezen függvény segítségével lehet vektorok hosszát és hajlásszögét definiálni, beszélni hossztartó leképezésekről, másképpen izometriákról vagy egybevágóságokról.
Visszatérve az euklideszi geometriára, a Hilbert által felállított és azóta is leginkább használt szintetikus axiómarendszer (ld. pld [9]) analitikus modelljét a következőképpen kaphatjuk:
Legyen ![]() egy halmaz,
egy halmaz, ![]() pedig egy
pedig egy ![]() -dimenziós euklideszi vektortér a valós számtest felett. Az
-dimenziós euklideszi vektortér a valós számtest felett. Az ![]() halmazt
halmazt ![]() -dimenziós euklideszi térnek nevezzük, ha pontjaiból alkotott rendezett
-dimenziós euklideszi térnek nevezzük, ha pontjaiból alkotott rendezett ![]() párok megfeleltethetők úgy a
párok megfeleltethetők úgy a ![]() -beli
-beli ![]() vektoroknak, hogy
vektoroknak, hogy
- minden
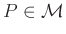 ,
,  esetén legyen egyetlen
esetén legyen egyetlen 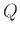 úgy, hogy
úgy, hogy 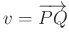 teljesüljön,
teljesüljön, - minden
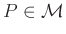 pont esetén, a
pont esetén, a 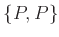 párnak a 0 vektor feleljen meg,
párnak a 0 vektor feleljen meg, - és minden
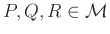 hármas esetén teljesüljön a
hármas esetén teljesüljön a 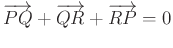 összefüggés.
összefüggés.
Mivel a skaláris szorzat egy vektorpárokon értelmezett valós értékű pozitív definit, szimmetrikus, mindkét változójában lineáris függvény, a nem nulla vektorokhoz hozzárendelhető egy pozitív ![]() szám, amelyet a vektor hossznégyzetének nevezünk. (A hossz jelölésére az
szám, amelyet a vektor hossznégyzetének nevezünk. (A hossz jelölésére az ![]() jelölést használva
jelölést használva ![]() .) A fenti három tulajdonság segítségével igazolható az ún. Cauchy-Schwarz-Bunyakovszkij-egyenlőtlenség, miszerint tetszőleges
.) A fenti három tulajdonság segítségével igazolható az ún. Cauchy-Schwarz-Bunyakovszkij-egyenlőtlenség, miszerint tetszőleges ![]() vektorpárra igaz, hogy
vektorpárra igaz, hogy ![]() , röviden
, röviden ![]() . Ebből rögtön adódik, hogy az
. Ebből rögtön adódik, hogy az ![]() kifejezés értelmes minden, nullát nem tartalmazó vektorpárra, és egy egyértelműen létező 0 és
kifejezés értelmes minden, nullát nem tartalmazó vektorpárra, és egy egyértelműen létező 0 és ![]() közötti szögértéket ad. Ezt hívjuk a vektorpár hajlásszögének. A
közötti szögértéket ad. Ezt hívjuk a vektorpár hajlásszögének. A ![]() a nem nulla vektorokra kapott
a nem nulla vektorokra kapott ![]() esetben adódik, így a skaláris szorzat egyszerűen jellemzi a „merőlegességet”. Az euklideszi vektortér speciális bázisa az ortonormált bázis, melyet páronként merőleges egységnyi hosszú vektorok alkotnak. Az ortonormált bázisról ortonormált bázisra való áttérés olyan lineáris transzformációval valósul meg, mely a vektorok hosszát nem változtatja meg, ezek a leképezések adják az euklideszi tér egybevágóságait vagy másképp izometriáit. Az izometriák csoportot alkotnak, melynek ismerete azért fontos, mert minden geometria keretein belül azonosnak tekintjük az egybevágó (vagy izometrikus) alakzatokat.
esetben adódik, így a skaláris szorzat egyszerűen jellemzi a „merőlegességet”. Az euklideszi vektortér speciális bázisa az ortonormált bázis, melyet páronként merőleges egységnyi hosszú vektorok alkotnak. Az ortonormált bázisról ortonormált bázisra való áttérés olyan lineáris transzformációval valósul meg, mely a vektorok hosszát nem változtatja meg, ezek a leképezések adják az euklideszi tér egybevágóságait vagy másképp izometriáit. Az izometriák csoportot alkotnak, melynek ismerete azért fontos, mert minden geometria keretein belül azonosnak tekintjük az egybevágó (vagy izometrikus) alakzatokat.
Modellünkben a pontpárokkal szeretnénk az egyeneseket, félegyeneseket és szakaszokat definiálni. Ehhez rögzítünk egy ![]() pontot (amelyet origónak vagy kezdőpontnak nevezünk) és egy kiindulási ortonormált bázist
pontot (amelyet origónak vagy kezdőpontnak nevezünk) és egy kiindulási ortonormált bázist ![]() elemekkel. A tér
elemekkel. A tér ![]() pontjához most a
pontjához most a ![]() helyvektor tartozik, mely az
helyvektor tartozik, mely az ![]() bázisra vonatkozó koordinátahármasával adott. A
bázisra vonatkozó koordinátahármasával adott. A ![]() pontok összekötő egyenesének tetszőleges
pontok összekötő egyenesének tetszőleges ![]() pontja megadható mint az
pontja megadható mint az ![]() helyvektor végpontja, ahol
helyvektor végpontja, ahol ![]() . Ha az
. Ha az ![]() együtthatókról feltesszük, hogy nem negatívak, akkor a fenti affin lineáris kombináció az ún. konvex kombinációvá válik, melyhez tartozó pontok összességeként definiálhatjuk a szakaszt. Három lineárisan független vektor affin kombinációi adják a három pont által kifeszített sík pontjait. A szakaszok egybevágóságát a hozzájuk rendelt vektorok hosszainak egyenlőségével definiálhatjuk. A szögvonalak és szögtartományok megadása után meg lehet fogalmazni ezek egybevágóságának analitikus feltételét is. Ezen az úton az ismert szintetikus geometriai tételek az analitikus modellben is leírhatók, ugyanakkor a szintetikus gondolatmenetek algebrai számításokkal helyettesítődnek.
együtthatókról feltesszük, hogy nem negatívak, akkor a fenti affin lineáris kombináció az ún. konvex kombinációvá válik, melyhez tartozó pontok összességeként definiálhatjuk a szakaszt. Három lineárisan független vektor affin kombinációi adják a három pont által kifeszített sík pontjait. A szakaszok egybevágóságát a hozzájuk rendelt vektorok hosszainak egyenlőségével definiálhatjuk. A szögvonalak és szögtartományok megadása után meg lehet fogalmazni ezek egybevágóságának analitikus feltételét is. Ezen az úton az ismert szintetikus geometriai tételek az analitikus modellben is leírhatók, ugyanakkor a szintetikus gondolatmenetek algebrai számításokkal helyettesítődnek.
A XIX. század végére a szisztematikus és szinte mindenre kiterjedő ![]() -dimenziós analitikus geometria vizsgálatok olyan tételek bizonyítását tették lehetővé, melyek szintetikus eszközökkel elérhetetlennek tűntek. Az érdeklődők számára ajánlom Salmon [15] könyvét a téma további tanulmányozására.
-dimenziós analitikus geometria vizsgálatok olyan tételek bizonyítását tették lehetővé, melyek szintetikus eszközökkel elérhetetlennek tűntek. Az érdeklődők számára ajánlom Salmon [15] könyvét a téma további tanulmányozására.
Hatalmas előnye az analitikus modellnek, hogy lényegében egyöntetűen kezelhető vele a sík és a tér esete, teret engedve a többdimenziós általánosításoknak is.
Szférikus geometria
A gömb az egyik legtökéletesebb forma minden kor embere számára. Már az egyiptomi tudósok is foglalkoztak vele, többek között meg szerették volna határozni a félgömb felszínét. Az Elemek c. könyvében Eukleidész a gömb térfogatának számítása mellett a szabályos testek köré írható gömbök sugarát is meghatározza. Az újkori matematika számtalan helyen kényszerült arra, hogy a gömb felületére rajzolt alakzatok különféle adatait határozza meg, ezért ezen számítások gyors elvégzése érdekében szisztematikus vizsgálat tárgyává tette a gömbfelszínt. Casey remek gyűjteménye (ld. [4]) a mai kor geométere számára is tartalmaz meglepetéseket. A „szférikus geometria” kifejezés ma is olyan állítások gyűjteményét jelenti, melyek a gömbfelszín alakzatainak metrikus tulajdonságairól szólnak. Ennek fő oka, hogy Hilbert axiómarendszere már az első axiómájában sérül, ha egyenesnek tekintjük a főköröket, két átellenes pont nem határoz meg egyértelműen egy egyenest. Ha viszont mesterségesen javítjuk ezt a „hibát”, azzal a feltevéssel, hogy két átellenes pont határozzon meg azonos modellpontot, akkor elveszítjük az egyenes egyik legfontosabb tulajdonságát, nem fogja a síkot két összefüggő részre vágni a továbbiakban. Így egy belső axiomatikus felépítés egy gyakorlatban jól alkalmazható metrikus struktúrától túl messzire visz, az így kapott ún. elliptikus geometria nem más, mint a valós projektív sík geometriája. A felületi alakzatok metrikus tulajdonságai ezen geometria keretein belűl többé-kevésbé érdektelenné válnak. Ezért a szférikus geometria megalapozásának legtermészetesebb módja továbbra is az, ha a tér felületének tekintjük. Ez a legegyszerűbb olyan felület, amelyet Gauss felületelméleti vizsgálatainak érdemes alávetni. Ezen vizsgálat lokális jellegű, ezért a teljes gömbfelszín egyben való kezelése során feltárt globális problémák (mint az egyenes határozatlansága) nem okoznak nehézséget. Kiderül, hogy minden pontjában a Gauss által definiált alapmennyiségek és alapformák ugyanazokat az értéket veszik fel, így a Gauss-féle szorzatgörbület minden pontban ugyanazt a pozitív értéket veszi fel, a gömb sugarának a reciprokát. Ezen tulajdonság alapján a szférikus geometriát pozitív konstans görbületű felületnek is szokták nevezni. (Jegyezzük meg, hogy az euklideszi sík beágyazva a háromdimenziós térbe konstans zéró görbületű felület.)
Ahhoz, hogy a szférikus és a későbbiekben szereplő hiperbolikus geometria közötti metrikus kapcsolatot észrevehessük, konkrét formulákat kell felírnunk.
Az ![]() -sugarú szférát definiáljuk azon
-sugarú szférát definiáljuk azon ![]() helyvektorok végpontjainak halmazaként, melyek teljesítik az
helyvektorok végpontjainak halmazaként, melyek teljesítik az ![]() feltételt. Egyeneseknek tekintjük a teljes főköröket, két pont két szakaszt határoz meg, ezek uniója az egyenes. Két pont távolságát és két egyenes hajlásszögét egyaránt euklideszi szöggel mérjük, az első a két helyvektor hajlásszöge, a második az egyeneseket tartalmazó két sík hajlásszöge. Szögtartományok hajlásszöge az őket tartalmazó térnegyedek szöge, így mind a szakaszhosszak, mind a szögmértékek a 0 és
feltételt. Egyeneseknek tekintjük a teljes főköröket, két pont két szakaszt határoz meg, ezek uniója az egyenes. Két pont távolságát és két egyenes hajlásszögét egyaránt euklideszi szöggel mérjük, az első a két helyvektor hajlásszöge, a második az egyeneseket tartalmazó két sík hajlásszöge. Szögtartományok hajlásszöge az őket tartalmazó térnegyedek szöge, így mind a szakaszhosszak, mind a szögmértékek a 0 és ![]() értékek között mozognak. Egy gömbháromszög szögösszege legalább
értékek között mozognak. Egy gömbháromszög szögösszege legalább ![]() és legfeljebb
és legfeljebb ![]() . Egyik határ sem éretik el valódi háromszög szögösszegeként. Számításuk a beágyazó euklideszi tér analitikus geometriája alapján történik, ha
. Egyik határ sem éretik el valódi háromszög szögösszegeként. Számításuk a beágyazó euklideszi tér analitikus geometriája alapján történik, ha ![]() két pont a
két pont a ![]() helyvektorokkal, akkor a távolságuk a
helyvektorokkal, akkor a távolságuk a
 avagy
avagy 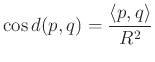
formulákból adódik. A trigonometrikus függvények használatával önálló trigonometrikus formulákat tudunk felírni a háromszögek adatainak összekapcsolására, amelyekben jelentkezik a szögek és távolságok számításának szimmetriája. Ha ![]() egy gömbháromszög három oldalának a hossza,
egy gömbháromszög három oldalának a hossza, ![]() pedig az ezekkel szemben fekvő szögek mértéke, két koszinusztétel adódik az egyik az oldalakra:
pedig az ezekkel szemben fekvő szögek mértéke, két koszinusztétel adódik az egyik az oldalakra:
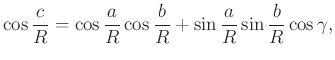
a másik a szögekre:
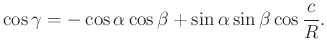
Az első egyenlet ![]() határátmenete azt árulja el, hogy a gömbsugárhoz képest kis oldalak esetén a háromszögre az euklideszi koszinusztétel teljesül, hiszen a trigonometrikus függvényeket a másodrendű Taylor polinomjukkal helyettesítve az
határátmenete azt árulja el, hogy a gömbsugárhoz képest kis oldalak esetén a háromszögre az euklideszi koszinusztétel teljesül, hiszen a trigonometrikus függvényeket a másodrendű Taylor polinomjukkal helyettesítve az
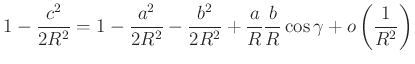
egyenlőségre jutunk. A ![]() oldal hosszához képest nagy
oldal hosszához képest nagy ![]() -re a második egyenlet a
-re a második egyenlet a ![]() , egyenletre vezet, mutatva, hogy ha legalább az egyik oldala egy szférikus háromszögnek nagyon kicsi, akkor a szögeire vagy
, egyenletre vezet, mutatva, hogy ha legalább az egyik oldala egy szférikus háromszögnek nagyon kicsi, akkor a szögeire vagy ![]() , vagy
, vagy ![]() áll fenn. Az első eset azt jelenti, hogy a háromszög szögeinek összege közel
áll fenn. Az első eset azt jelenti, hogy a háromszög szögeinek összege közel ![]() , míg a második esetben a háromszög szögeinek összege
, míg a második esetben a háromszög szögeinek összege ![]() . Szemléltethetjük ezen két lehetőséget, ha egy
. Szemléltethetjük ezen két lehetőséget, ha egy ![]() szögű gömbkétszöget az egyik csúcsához közel haladó gömbi egyenessel két gömbi háromszögre bontunk. A kisebbik rész valamennyi oldala pici, ez így egy euklideszi háromszöghöz áll közel, ennek
szögű gömbkétszöget az egyik csúcsához közel haladó gömbi egyenessel két gömbi háromszögre bontunk. A kisebbik rész valamennyi oldala pici, ez így egy euklideszi háromszöghöz áll közel, ennek ![]() szögeire az
szögeire az ![]() összefüggés teljesül, akkor viszont a nagyobbik rész szögei
összefüggés teljesül, akkor viszont a nagyobbik rész szögei ![]() a
a ![]() -hoz közeli szögösszeggel.
-hoz közeli szögösszeggel.
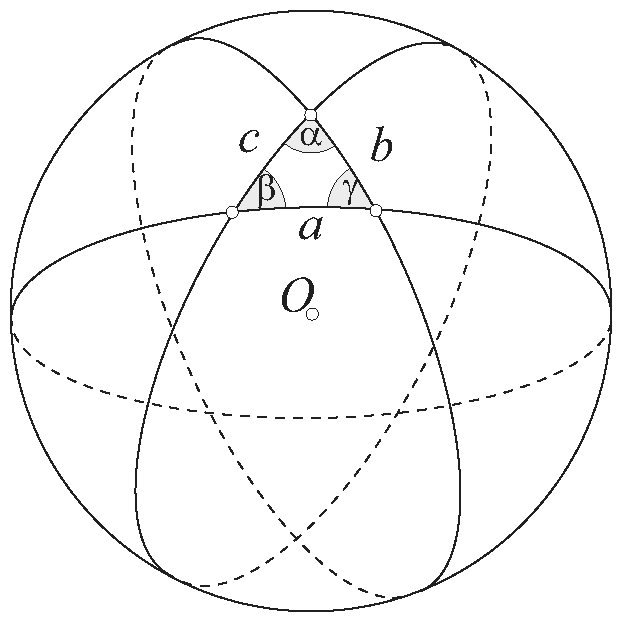 Különösen érdekes a szférikus sík geometriájában a háromszög területe. A gömbkétszöget egyetlen adata határozza meg, az
Különösen érdekes a szférikus sík geometriájában a háromszög területe. A gömbkétszöget egyetlen adata határozza meg, az ![]() szöge. Területe így szintén ennek a függvénye. Ez a
szöge. Területe így szintén ennek a függvénye. Ez a ![]() függvény additív és monoton, azaz lineáris. Ez azt jelenti, hogy
függvény additív és monoton, azaz lineáris. Ez azt jelenti, hogy ![]() alakú, ahol
alakú, ahol ![]() egy pozitív konstans. Az
egy pozitív konstans. Az ![]() eset a félgömböt adja, így ha a felszín euklideszi számításával kompatibilis területfogalmat szeretnénk kialakítani, akkor célszerű a
eset a félgömböt adja, így ha a felszín euklideszi számításával kompatibilis területfogalmat szeretnénk kialakítani, akkor célszerű a ![]() választás. Egy
választás. Egy ![]() szögekkel rendelkező háromszög három gömbkétszög metszete, ezek szögei rendre
szögekkel rendelkező háromszög három gömbkétszög metszete, ezek szögei rendre ![]() és
és ![]() . Ugyanezen gömbkétszögek az origóra vonatkozó tükörképeikkel együtt lefedik a gömböt oly módon, hogy a kiindulási háromszöget éppen az eredeti három gömbkétszög, míg a háromszög tükörképét a három tükörkép fedi. Ez alapján a keresett
. Ugyanezen gömbkétszögek az origóra vonatkozó tükörképeikkel együtt lefedik a gömböt oly módon, hogy a kiindulási háromszöget éppen az eredeti három gömbkétszög, míg a háromszög tükörképét a három tükörkép fedi. Ez alapján a keresett ![]() területre fennáll a
területre fennáll a
összefüggés.
Tekintettel az euklideszi térbe való beágyazottságra, a szférikus geometria egybevágóságai könnyen adódnak, ezek éppen azok az euklideszi egybevágóságok, melyek a modellgömböt saját magára képezik. Ezek adják az ortogonális csoportot, melyet az origón átmenő egyenesek körüli forgatások, illetve az origóra vonatkozó tükrözés generál.
A Bolyai–Lobacsevszkij-féle hiperbolikus geometria
Annak ellenére, hogy az euklideszi rendszer remek egyezést mutat a mérhető világgal, már Eukleidész informál minket arról, hogy nem minden alapállítást kell (lehet) azonos szinten kezelni. Az axiómák mellett (melyeket mindenki számára kötelezően elfogadandónak tart) használja a Posztulátum megnevezést is, mely gyengébb elfogadási szintet jelent. A vitában résztvevő felek egyike további gondolatmenetét valamely Posztulátumra alapozva, fenntartja a lehetőségét annak, hogy esetleg később ezen állítását revideálva új eredményre jusson. Az V. Posztulátum egy ilyen állítás. Ennek a i.sz. 300 körül élő Proklosztól származó párhuzamossági axiómának nevezett alakja a legismertebb. Eszerint egy sík egy adott pontján keresztül, egy a ponton nem áthaladó adott síkbeli egyeneshez pontosan egy az adott ponton áthaladó és az adott egyenest nem metsző egyenest találunk. Az V. Posztulátum igaz (a többi axiómákból igazolható) vagy hamis (a többi axiómákból nem igazolható) voltának eldöntésére tett kísérletek a matematika történetét 2 évezreden át gazdagították. A bőséges irodalomra tekintettel meg sem kíséreljük ezeket reprodukálni, javasoljuk azonban a közismert magyarul megjelent könyvek ([2], [1], [16]) mellett, egy ezzel a céllal íródott cikk elolvasását (ld. [10]) is. Annyit azonban mi is megemlítünk, hogy a két évezredes probléma a XIX. század első harmadának a végén oldódik meg. Bolyai János 1823-ban újságolja el levélben apjának felfedezését; 1826-ban küldi el német nyelven írt kéziratát volt tanárának; illetve nyomtatásban latin nyelven 1831-ben jelenteti meg apjának könyvéhez csatolt függelékként. Lényegében egyidőben, de attól függetlenül Nyikoláj Ivanovics Lobacsevszkij hasonló elméletével, melynek első nyomai egy 1823-as tankönyvében találhatók; teljességgel pedig egy 1835-ben kiadott Képzetes Geometria c. könyvben publikálódott. Bolyai felfedezése lényegében elakadt Gaussnál, néhány rövid soron kívül (amit Bolyai Farkasnak írt) sose beszélt ezen eredményről, nem említette Lobacsevszkijnek sem, akinek 1840-ben német nyelven írt összefoglalóját olvasta és terjesztette is. (Ez a munka Bolyaihoz 1848-ban jutott el.)
Mindketten igazolták, hogy van logikailag egyenértékű alternatívája az euklideszi síkgeometriának. Lobacsevszkij felépített egy elképzelt geometriát, melyben alapállításként a párhuzamossági axióma tagadását teszi fel, igazolja, hogy geometriájában a háromszögek szögösszege ![]() -nél kisebb, kidolgozza a háromszögek trigonometriáját, és fontos lépéseket tesz a terület és térfogat számítások tárgykörében. Bolyai elhagyja a párhuzamossági axiómát és felépíti azt az abszolút geometriának nevezett geometriát, mely ezen axiómától független állításokat tartalmaz. A párhuzamossági axióma ebben a rendszerben egy elágazási pont, feltéve igaz voltát az euklideszi geometriához, tagadva azt egy másik az ún. hiperbolikus geometriához jutunk. Ezen utóbbi megegyezik Lobacsevszkij elképzelt geometriájával. Igazolja a két geometria relatív ellentmondás-mentességét. (A két fontos dolgozat állításait egyaránt megtaláljuk a [8] könyvben.)
-nél kisebb, kidolgozza a háromszögek trigonometriáját, és fontos lépéseket tesz a terület és térfogat számítások tárgykörében. Bolyai elhagyja a párhuzamossági axiómát és felépíti azt az abszolút geometriának nevezett geometriát, mely ezen axiómától független állításokat tartalmaz. A párhuzamossági axióma ebben a rendszerben egy elágazási pont, feltéve igaz voltát az euklideszi geometriához, tagadva azt egy másik az ún. hiperbolikus geometriához jutunk. Ezen utóbbi megegyezik Lobacsevszkij elképzelt geometriájával. Igazolja a két geometria relatív ellentmondás-mentességét. (A két fontos dolgozat állításait egyaránt megtaláljuk a [8] könyvben.)
Elképzelést kapni a hiperbolikus geometriáról több módón is lehetséges. Bolyai útja hosszadalmas, hiszen számos kisebb-nagyobb állítás bizonyítása formálja apránként szemléletünket mindaddig, míg természetesnek nem vesszük, hogy a síkon három lényegesen különböző lehetőség adódik két egyenes kölcsönös helyzetére; hogy a háromszögek szögösszege 0 és ![]() között bármilyen értéket felvehet; és nincs akármilyen nagy területű háromszög, nem beszélhetünk hasonlóságról.
között bármilyen értéket felvehet; és nincs akármilyen nagy területű háromszög, nem beszélhetünk hasonlóságról.
A modell módszer ezt az utat lerövidíti. A hiperbolikus geometria adaptálására a leggyakrabban használt modell a Cayley-Klein- vagy projektív modell. Az euklideszi sík egy ![]() -sugarú körének belső pontjait tekintjük pontoknak, az egyenesek pedig a körbe metsző egyenesek körön belüli részei. Azonnal látható, hogy ebben a modellben nem teljesül a párhuzamossági axióma. A síkgeometria szokásos objektumai könnyen beazonosíthatók, de számítások elvégzéséhez szükségünk van a szakaszhossz és szögmérték megadására is. Ha
-sugarú körének belső pontjait tekintjük pontoknak, az egyenesek pedig a körbe metsző egyenesek körön belüli részei. Azonnal látható, hogy ebben a modellben nem teljesül a párhuzamossági axióma. A síkgeometria szokásos objektumai könnyen beazonosíthatók, de számítások elvégzéséhez szükségünk van a szakaszhossz és szögmérték megadására is. Ha ![]() két pontja a körnek, akkor az összekötő egyenesük két további pontban metszi a körvonalat, legyenek ezek
két pontja a körnek, akkor az összekötő egyenesük két további pontban metszi a körvonalat, legyenek ezek ![]() . Tegyük fel, hogy
. Tegyük fel, hogy ![]() és
és ![]() között van a
között van a ![]() pont. Ekkor előjeles távolságokban gondolkozva is pozitív a
pont. Ekkor előjeles távolságokban gondolkozva is pozitív a
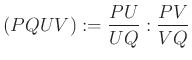
hányados, melyet a négy pont kettősviszonyának nevezünk. A kettősviszony rendelkezik a ![]() „multiplikatív” tulajdonsággal. Mivel a vizsgált kettősviszonyok pozitívak, értelmes a
„multiplikatív” tulajdonsággal. Mivel a vizsgált kettősviszonyok pozitívak, értelmes a ![]() megfeleltetés, melyre ezért a
megfeleltetés, melyre ezért a ![]() egyenlőség is teljesül. A pontok távolságának értelmezése tehát a
egyenlőség is teljesül. A pontok távolságának értelmezése tehát a ![]() formulával történhet, ahol a
formulával történhet, ahol a ![]() konstans meghatározása még hátravan. Ha modellkörünk
konstans meghatározása még hátravan. Ha modellkörünk ![]() sugarú, a
sugarú, a ![]() pontot a kör középpontjának választva, a
pontot a kör középpontjának választva, a ![]() euklideszi távolságot pedig
euklideszi távolságot pedig ![]() -el jelölve, az
-el jelölve, az ![]() -hez tartozó
-hez tartozó ![]() modelltávolság a
modelltávolság a
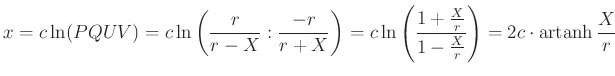
formulával számolható. Ha ![]() -t
-t ![]() -nek választjuk, ez a formula a szimmetrikus
-nek választjuk, ez a formula a szimmetrikus
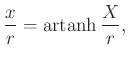 avagy
avagy 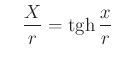
alakot ölti.
 A Cayley–Klein-modellben a Hilbert-féle axiómák ellenőrzése nem okoz nehézséget, ha közvetlenül definiáljuk a szögtartományok egybevágóságát. Azonban a szögtartományoknak olyan mértéket adni, melynek alapján a hiperbolikus trigonometria levezethető, nem magától értetődő feladat. Felix Klein, Cayley kúpszeletekre vonatkozó relatív távolságfogalmát alkalmazta modelljén, ezért dualitást követelt a távolság és szögmérték meghatározásának tekintetében. Azaz egy adott sugársorhoz hozzá kellett rendelnie két egyenest, amelyek a szög szárait adó sugársorbeli elemekkel együtt négy olyan egyenest jelentettek, melyeknek kettősviszonya definiált. Ezek az extra egyenesek az alapkúpszelethez a sugársor tartópontjából húzott érintők. A négy egyenes kettősviszonyának alkalmas logaritmusa a szög mértékét a pontok távolságának módján definiálhatja. Hiperbolikus metsző egyenespár közös pontjai a modell belső pontjai, ezért a szöget adó sugársornak nincs olyan egyenese, mely szokásos értelemben érinthetné a modellkört. De ha komplex együtthatókat is megengedünk, éppen két ilyet találunk.
A Cayley–Klein-modellben a Hilbert-féle axiómák ellenőrzése nem okoz nehézséget, ha közvetlenül definiáljuk a szögtartományok egybevágóságát. Azonban a szögtartományoknak olyan mértéket adni, melynek alapján a hiperbolikus trigonometria levezethető, nem magától értetődő feladat. Felix Klein, Cayley kúpszeletekre vonatkozó relatív távolságfogalmát alkalmazta modelljén, ezért dualitást követelt a távolság és szögmérték meghatározásának tekintetében. Azaz egy adott sugársorhoz hozzá kellett rendelnie két egyenest, amelyek a szög szárait adó sugársorbeli elemekkel együtt négy olyan egyenest jelentettek, melyeknek kettősviszonya definiált. Ezek az extra egyenesek az alapkúpszelethez a sugársor tartópontjából húzott érintők. A négy egyenes kettősviszonyának alkalmas logaritmusa a szög mértékét a pontok távolságának módján definiálhatja. Hiperbolikus metsző egyenespár közös pontjai a modell belső pontjai, ezért a szöget adó sugársornak nincs olyan egyenese, mely szokásos értelemben érinthetné a modellkört. De ha komplex együtthatókat is megengedünk, éppen két ilyet találunk.
Legyen az adott pont a modellkör középpontja és a modellkört adja meg az ![]() egyenlet valamilyen Descartes-féle koordináta-rendszerre nézve. A keresett egyenesek egyenlete
egyenlet valamilyen Descartes-féle koordináta-rendszerre nézve. A keresett egyenesek egyenlete ![]() alakú, ahol
alakú, ahol ![]() komplex szám is lehet. Ebből kapjuk az
komplex szám is lehet. Ebből kapjuk az ![]() egyenletet, melyben
egyenletet, melyben ![]() -t úgy kell megválasztani, hogy a
-t úgy kell megválasztani, hogy a ![]() diszkrimináns zérus legyen. Azaz
diszkrimináns zérus legyen. Azaz ![]() és a keresett komplex érintők
és a keresett komplex érintők ![]() , ahol
, ahol ![]() . Az origón átmenő tetszőleges két, modellbeli, egymással
. Az origón átmenő tetszőleges két, modellbeli, egymással ![]() euklideszi szöget bezáró egyenes analitikusan megadható az
euklideszi szöget bezáró egyenes analitikusan megadható az ![]() ,
, ![]() egyenletekkel. A négy egyenes kettősviszonya a Pappos-Steiner-tétel alapján megkapható teszőleges tőlük különböző egyenessel való metszetpontnégyes kettősviszonyával. Válasszuk ezen segédegyenesnek az
egyenletekkel. A négy egyenes kettősviszonya a Pappos-Steiner-tétel alapján megkapható teszőleges tőlük különböző egyenessel való metszetpontnégyes kettősviszonyával. Válasszuk ezen segédegyenesnek az ![]() egyenest. Ez rendre a
egyenest. Ez rendre a ![]() pontokban metszi sugárnégyesünket. A négy pont (komplex) kettősviszonya tehát:
pontokban metszi sugárnégyesünket. A négy pont (komplex) kettősviszonya tehát:

amiből a hajlásszög definíciója alapján a
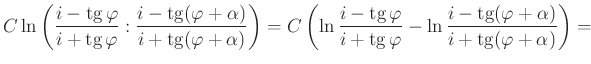
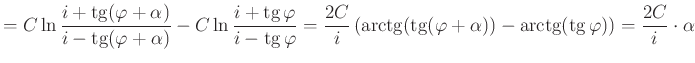
végeredmény adódik. Ha ![]() -t
-t ![]() -nek választjuk, a modellközéppontban találkozó egyenesek hiperbolikus és euklideszi hajlásszöge megegyezik. A kapott szögmérték használatával már igazolhatók a hiperbolikus háromszög trigonometrikus formulái, a két koszinusztétel az alábbi alakot ölti:
-nek választjuk, a modellközéppontban találkozó egyenesek hiperbolikus és euklideszi hajlásszöge megegyezik. A kapott szögmérték használatával már igazolhatók a hiperbolikus háromszög trigonometrikus formulái, a két koszinusztétel az alábbi alakot ölti:
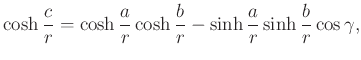
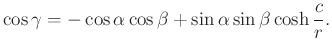
Azonnal feltűnik a gömbi geometria koszinusztételeivel való hasonlóság. Az ismert
azonosságok használatával a gömbi formulákból az ![]() helyettesítés olyan hiperbolikus formulákhoz vezet, melyek határesete megint egy euklideszi formula. Ez arra utal, hogy a hiperbolikus és a szférikus terek az
helyettesítés olyan hiperbolikus formulákhoz vezet, melyek határesete megint egy euklideszi formula. Ez arra utal, hogy a hiperbolikus és a szférikus terek az ![]() paraméter megfeleltetéssel párokba rendezhetők, ahol
paraméter megfeleltetéssel párokba rendezhetők, ahol ![]() esetén ezen geometriák közös határhelyzete az euklideszi geometria. Az analógiát használva a háromszög területére vonatkozó gömbi formula a hiperbolikus
esetén ezen geometriák közös határhelyzete az euklideszi geometria. Az analógiát használva a háromszög területére vonatkozó gömbi formula a hiperbolikus ![]() szögekkel rendelkező háromszög területére nézve a jól ismert defektusra vonatkozó formulát adja:
szögekkel rendelkező háromszög területére nézve a jól ismert defektusra vonatkozó formulát adja:
Feltétlenül említenünk kell ezen a ponton Lambert nevét, aki abból a feltételezésből kiindulva, hogy a háromszög szögösszege kisebb mint ![]() lényegében levezette a terület fenti kifejezését. Ő jött rá arra, hogy a „képzetes sugarú gömb” geometriája produkál a várt nemeuklideszi szintetikus észrevételekhez passzoló modellt ([12]). Mindazonáltal ezen lehetőség megvalósulását „igazi” geometria modellel nem tudta alátámasztani. A Cayley–Klein-modell jelentősége, hogy a hiperbolikus sík egésze tekintetében bizonyítható vele a relatív ellentmondástalanság, a hiperbolikus geometriában fellépő ellentmondás az euklideszi geometria ellentmondásaként is jelentkezne.
lényegében levezette a terület fenti kifejezését. Ő jött rá arra, hogy a „képzetes sugarú gömb” geometriája produkál a várt nemeuklideszi szintetikus észrevételekhez passzoló modellt ([12]). Mindazonáltal ezen lehetőség megvalósulását „igazi” geometria modellel nem tudta alátámasztani. A Cayley–Klein-modell jelentősége, hogy a hiperbolikus sík egésze tekintetében bizonyítható vele a relatív ellentmondástalanság, a hiperbolikus geometriában fellépő ellentmondás az euklideszi geometria ellentmondásaként is jelentkezne.
Gauss számára a szférikus geometria konkrét példát jelentett konstans pozitív görbületű felületre az euklideszi térben. Ez azért is fontos, mert felületelméletében kidolgozott egy szép tételt, mely a háromszög szögösszegét számítja ki a szorzatgörbület segítségével. A felület belső geometriájában egyenes szakasznak tekintendő egy felületen haladó két felületi pontot összekötő legrövidebb görbe vonal, melyet geodetikusnak szoktak nevezni. A geodetikus vonalakkal összekötött három pont a háromszög, ennek szögeit az egy csúcsban találkozó geodetikusok érintőinek hajlásszöge méri. Gauss tétele szerint az ![]() ,
, ![]() ,
, ![]() szögekkel bíró geodetikus háromszög szögösszegét az
szögekkel bíró geodetikus háromszög szögösszegét az

formulával lehet meghatározni, ahol a ![]() függvény a felület szorzatgörbülete,
függvény a felület szorzatgörbülete, ![]() a felszínéből származó mérték,
a felszínéből származó mérték, ![]() pedig az a paramétertartomány az
pedig az a paramétertartomány az ![]() síkon, melyből a háromszögtartomány pontjai adódnak. (Egy pontosabb, könnyen érthető leírás Szenthe János cikkében található az [1] könyvben.) Így Gauss a gömb esetében megkapta a terület formulát, hiszen ekkor
síkon, melyből a háromszögtartomány pontjai adódnak. (Egy pontosabb, könnyen érthető leírás Szenthe János cikkében található az [1] könyvben.) Így Gauss a gömb esetében megkapta a terület formulát, hiszen ekkor ![]() és
és ![]() . Ezek szerint a
. Ezek szerint a ![]() -dimenziós euklideszi térben van olyan felületet, amelynek a belső (felületként való előállítástól független) geometriája konstans pozitív görbületű, így a háromszögeinek területe a szögösszegének a többletével arányos, és van olyan felületünk is, ahol ez a szögösszeg
-dimenziós euklideszi térben van olyan felületet, amelynek a belső (felületként való előállítástól független) geometriája konstans pozitív görbületű, így a háromszögeinek területe a szögösszegének a többletével arányos, és van olyan felületünk is, ahol ez a szögösszeg ![]() , mert a szorzatgörbület azonosan zérus (az euklideszi sík). Gauss arra nem látott példát, hogy olyan is létezik, ahol a terület a hiánnyal arányos, mert a szorzatgörbület konstans negatív értéket vesz fel. Ha a teljes hiperbolikus sík megadható egy felületdarabjaként az euklideszi térnek, könnyű olyan koordinátázását megadni, melyre Gauss formuláit kiszámolva konstans negatív szorzatgörbületet kapunk. Gauss ilyen felület keresése közben foglalkozhatott a hiperbolikus geometria körébe vezető problémákkal, de szisztematikus vizsgálatnak írott nyoma nincs munkásságában. Az Appendix olvasása döbbenthette arra rá, hogy „lekésett” a Lambert féle képzetes sugarú gömb megvalósítása kérdésében, mert a probléma megoldása csak az axiomatika útján lehetséges, de ezt Bolyai János megcsinálta. (E tárgykörben ajánlom a [6] cikket olvasásra.) Mindenesetre Gauss problémájának komoly utóélete lett. Jóval később Beltrami ad meg először olyan felületet, melynek belső geometriája a hiperbolikus sík egy darabjának felel meg (ld. [3]) majd ezt a konstrukciót számos másik követte. De egyik sem a teljes hiperbolikus sík ábrázolását adja. (Mai szaknyelven nem a hiperbolikus sík izometrikus immertálásával adódó felület.) 1900-ban bizonyítja Hilbert, hogy a
, mert a szorzatgörbület azonosan zérus (az euklideszi sík). Gauss arra nem látott példát, hogy olyan is létezik, ahol a terület a hiánnyal arányos, mert a szorzatgörbület konstans negatív értéket vesz fel. Ha a teljes hiperbolikus sík megadható egy felületdarabjaként az euklideszi térnek, könnyű olyan koordinátázását megadni, melyre Gauss formuláit kiszámolva konstans negatív szorzatgörbületet kapunk. Gauss ilyen felület keresése közben foglalkozhatott a hiperbolikus geometria körébe vezető problémákkal, de szisztematikus vizsgálatnak írott nyoma nincs munkásságában. Az Appendix olvasása döbbenthette arra rá, hogy „lekésett” a Lambert féle képzetes sugarú gömb megvalósítása kérdésében, mert a probléma megoldása csak az axiomatika útján lehetséges, de ezt Bolyai János megcsinálta. (E tárgykörben ajánlom a [6] cikket olvasásra.) Mindenesetre Gauss problémájának komoly utóélete lett. Jóval később Beltrami ad meg először olyan felületet, melynek belső geometriája a hiperbolikus sík egy darabjának felel meg (ld. [3]) majd ezt a konstrukciót számos másik követte. De egyik sem a teljes hiperbolikus sík ábrázolását adja. (Mai szaknyelven nem a hiperbolikus sík izometrikus immertálásával adódó felület.) 1900-ban bizonyítja Hilbert, hogy a ![]() -dimenziós euklideszi térben ilyen felület nem is létezik.
-dimenziós euklideszi térben ilyen felület nem is létezik.
Beltrami példája kellőképpen egyszerű, ahhoz, hogy vázlatosan tárgyaljuk. Tekintsünk egy tetszőleges pozitív ![]() valós számot és keressük az
valós számot és keressük az ![]() síknak olyan
síknak olyan ![]() görbéjét, mely átmegy az
görbéjét, mely átmegy az ![]() ponton és egy adott pontjában megrajzolt érintőjének az érintési pont és az
ponton és egy adott pontjában megrajzolt érintőjének az érintési pont és az ![]() -tengely által közrezárt szakasza éppen
-tengely által közrezárt szakasza éppen ![]() hosszúságú. A feltétel felírása után az ismeretlen függvényre az
hosszúságú. A feltétel felírása után az ismeretlen függvényre az
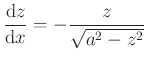
egyenlet adódik, melynek mindkét oldalát integrálva az
![$\displaystyle x(z)=\pm \left(a\ln\frac{a+\sqrt{a^2-z^2}}{z}-\sqrt{a^2-z^2}\right)=\pm \left(a\cdot \areasech\frac{z}{a}-\sqrt{a^2-z^2}\right) \quad z\in (0,a]
$](/images/stories/latex/236938f07521366862c9ea56954548a9_nemeuklideszigeometriak/img114.png)
explicit előállítást kapjuk. A kapott görbe a vonszolási görbe vagy traktrix, amelynek ![]() -tengely körüli megforgatottja származtatja a Beltrami-féle pszeudoszférát. A pszeudoszféra szorzat görbülete
-tengely körüli megforgatottja származtatja a Beltrami-féle pszeudoszférát. A pszeudoszféra szorzat görbülete ![]() , de az
, de az ![]() síkbeli körmetszetének pontjaiban nem léteznek azok az alapmennyiségek, melyekből a szorzatgörbület számítható. Így a hiperbolikus sík tetszőleges korlátos darabjának ábrázolására alkalmas, de a teljes síkéra nem.
síkbeli körmetszetének pontjaiban nem léteznek azok az alapmennyiségek, melyekből a szorzatgörbület számítható. Így a hiperbolikus sík tetszőleges korlátos darabjának ábrázolására alkalmas, de a teljes síkéra nem.
Utolsó megjegyzésként szeretném felhívni arra a figyelmet, hogy habár eddig az euklideszi geometriát tekintettük a másik kettő közötti határátmenetnek, erre nem feltétlenül kell így gondolni. Bolyai gondolatmenetében az euklideszi és hiperbolikus geometriák az édestestvérek, a közös tételeik alkotják a „tér abszolút és igaz tudományát”. A gömbi geometria lóg ki a sorból, ugyanakkor fontos közvetítő szerepe van. Világos, hogy a hiperbolikus téren belül is lehet önálló gömbi geometriát értelmezni, hiszen minden szükséges eszköz a kezünkben van ehhez. A kérdés az, hogy milyen kapcsolatban van egymással a hiperbolikus geometria és az euklideszi geometria gömbi geometriája. Bolyai először bizonyítja a szinusztétel mindkét geometriában érvényes abszolút alakját, majd ennek segítségével igazolja, hogy a gömbi trigonometria formulái egyaránt érvényesek a hiperbolikus és az euklideszi térben vizsgált gömbfelszíneken. Azaz a gömbi geometria abszolút érvényű!
A téridő modell
A XX. század eleje a világról alkotott statikus képet alaposan átformálta. Bernhard Riemann 1854-ben tartott habilitációs előadása olyan új lehetőséget tárt fel világképünk alakításához, amely ma is meghatározza azt. Felvázolta a Riemann-geometria alapgondolatát, mely úgy jelenik meg, mint a Gauss-féle felületgeometria olyan magasabb dimenziós általánosítása, mely független a beágyazással való realizálhatóságtól. A Riemann-geometriák dinamikusak abban az értelemben, hogy általános globális definíciójuk mellett metrikus szerkezetük pontról pontra változik, még a geodetikusok sem feltétlenül rendelkeznek általános érvénnyel, előfordulhat, hogy két pontot nem lehet geodetikussal összekötni. A XIX. század végének fizikája ezt a szemléletet erősíti. Sorban merülnek fel a kétségek a Newtoni fizika érvényességi körét illetően, míg Einstein meg nem fogalmazza először a speciális, majd az általános relativitáselméletet.
A téridő modell a speciális relativitáselmélethez kapcsolódó világról alkotott geometriai kép matematikai modellje. Hermann Minkowski javasolja használatát a [14] munkájában. Az euklideszi geometriában rögzíthetünk egy ortonormált bázist és egy hozzá kapcsolt Descartes-féle koordináta-rendszert, tekintve ezt a helymeghatározás abszolút rendszerének. Az euklideszi jellegért a kapcsolt euklideszi vektortér skaláris szorzatának három alaptulajdonsága felel. Ha azonban a világbeli pozíciónk leírására törekszünk, e három koordináta mellé egy negyediket is képzelnünk kell, mely azt az időpontot adja meg, amikor a vizsgált objektum az adott térbeli helyzetben volt. Egy részecskére gondolva egy ilyen négykoordinátás koordináta-rendszerben az első három koordináta a hol, az utolsó a mikor kérdésre ad választ. A kérdés az, hogy van-e olyan egységes számolási elv, mellyel az olyan geometriai fogalmak mint szakaszhossz, szögmérték, merőlegesség definiálhatók ilyen ![]() -vektorokra. Minkowski javaslata szerint négyeseinknek
-vektorokra. Minkowski javaslata szerint négyeseinknek ![]() -dimenziós vektortér feleljen meg azzal a változtatással, hogy a skaláris szorzás definícíójában szereplő, pozitív definitségi tulajdonságot elhagyjuk. Skaláris szorzatunk általában legyen egy nem elfajuló, valós értékű, szimmetrikus, bilineáris függvény (indefinit skaláris szorzat). A fizikai tér leírásához így elegendő az indefinit skaláris szorzat függvényt megadni, egy adott bázisra vonatkozó koordinátákra gyakorolt hatása segítségével. Az euklideszi skaláris szorzatot az jellemzi, hogy ortonormált bázisra vonatkozó koordináták esetén a helyvektorok hossznégyzete a koordináták négyzetösszegével egyezik meg. Azaz valamilyen bázisra nézve
-dimenziós vektortér feleljen meg azzal a változtatással, hogy a skaláris szorzás definícíójában szereplő, pozitív definitségi tulajdonságot elhagyjuk. Skaláris szorzatunk általában legyen egy nem elfajuló, valós értékű, szimmetrikus, bilineáris függvény (indefinit skaláris szorzat). A fizikai tér leírásához így elegendő az indefinit skaláris szorzat függvényt megadni, egy adott bázisra vonatkozó koordinátákra gyakorolt hatása segítségével. Az euklideszi skaláris szorzatot az jellemzi, hogy ortonormált bázisra vonatkozó koordináták esetén a helyvektorok hossznégyzete a koordináták négyzetösszegével egyezik meg. Azaz valamilyen bázisra nézve ![]() hossznégyzettel dolgozhatunk. Minkowski téridő modelljében az időnek megfelelő koordináta négyzetét levonjuk a térkoordináták négyzetösszegéből, azaz az adott bázisra vonatkozó koordinátákkal
hossznégyzettel dolgozhatunk. Minkowski téridő modelljében az időnek megfelelő koordináta négyzetét levonjuk a térkoordináták négyzetösszegéből, azaz az adott bázisra vonatkozó koordinátákkal ![]() teljesül. Hagyományos okokból az
teljesül. Hagyományos okokból az ![]() koordinátát
koordinátát ![]() -vel jelölve a skaláris szorzatunk számításának módja az
-vel jelölve a skaláris szorzatunk számításának módja az ![]() alakot ölti. Ebben a modellben háromfajta vektorunk van; azokat, amelyek hossznégyzete pozitív, nevezzük térszerűnek, amelyek hossznégyzete negatív, az időszerű vektorok, és amelyeknek hossznégyzete nulla, azok a fényszerű vektorok. A speciális relativitáselmélet keretein belűl a fizikai tér két megengedett vonatkoztatási rendszerében mért adatokat az ún. Lorentz-transzformáció köti össze. Minkowski modelljében reprezentálva a Lorentz-transzformációt azt kapjuk, hogy ezen vonatkoztatási rendszerekhez kapcsolt bázisok cseréje esetén az általuk definiált koordinátákkal Minkowski módján számított skalárnégyzet nem változik meg. (Megengedett két vonatkozási rendszer, ha az egyik a másikhoz viszonyítva egyenesvonalú egyenletes mozgást végez.)
alakot ölti. Ebben a modellben háromfajta vektorunk van; azokat, amelyek hossznégyzete pozitív, nevezzük térszerűnek, amelyek hossznégyzete negatív, az időszerű vektorok, és amelyeknek hossznégyzete nulla, azok a fényszerű vektorok. A speciális relativitáselmélet keretein belűl a fizikai tér két megengedett vonatkoztatási rendszerében mért adatokat az ún. Lorentz-transzformáció köti össze. Minkowski modelljében reprezentálva a Lorentz-transzformációt azt kapjuk, hogy ezen vonatkoztatási rendszerekhez kapcsolt bázisok cseréje esetén az általuk definiált koordinátákkal Minkowski módján számított skalárnégyzet nem változik meg. (Megengedett két vonatkozási rendszer, ha az egyik a másikhoz viszonyítva egyenesvonalú egyenletes mozgást végez.)
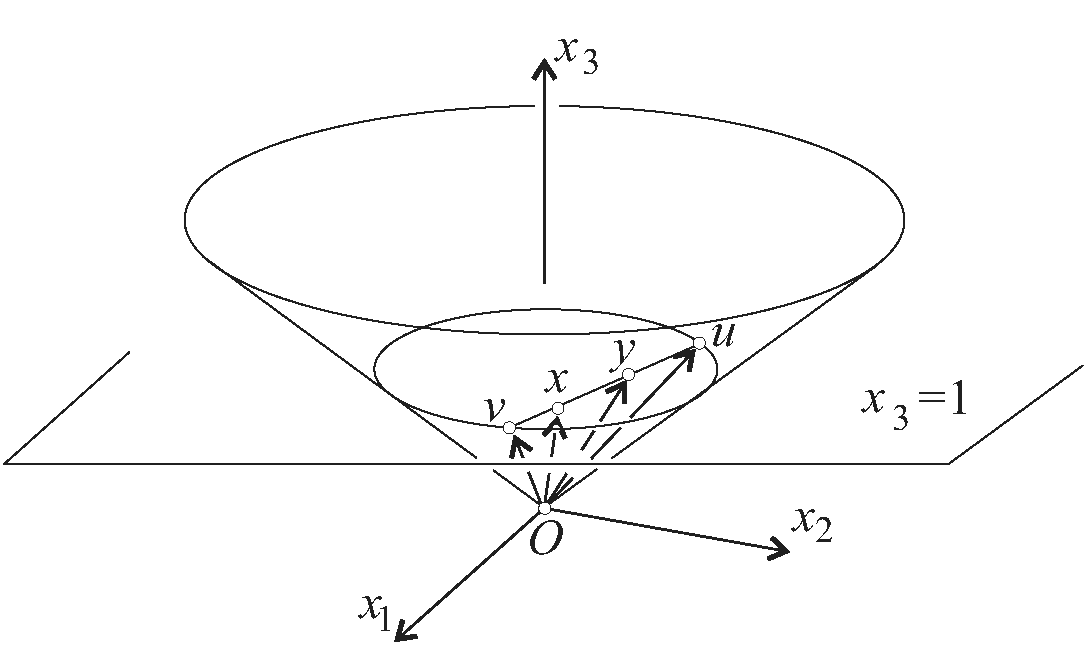
Minkowski modellje Gauss kérdését a hiperbolikus sík izometrikus immertálásáról új megvilágításba helyezi. Tekintsük ugyanis most az ![]() felületet az
felületet az ![]() koordináták elhagyásával kapott
koordináták elhagyásával kapott ![]() -dimenziós Minkowski-térben. Ennek minden érintősíkjára teljesül, hogy erre megszorítva az indefinit skaláris szorzatot, egy pozitív definit skaláris szorzatot kapunk. Azaz Gauss felületelméleti számításai alkalmazhatók rá, abban a formában, mint az euklideszi térben. Az is kiszámolható, hogy a szorzatgörbülete minden pontjában
-dimenziós Minkowski-térben. Ennek minden érintősíkjára teljesül, hogy erre megszorítva az indefinit skaláris szorzatot, egy pozitív definit skaláris szorzatot kapunk. Azaz Gauss felületelméleti számításai alkalmazhatók rá, abban a formában, mint az euklideszi térben. Az is kiszámolható, hogy a szorzatgörbülete minden pontjában ![]() . A kapott felület így egy modellje a teljes hiperbolikus síknak. Lambert algebrai ötlete a képzetes sugarú gömbröl a Minkowski-térben az egyik legfontosabb felület, a képzetes sugarú egységgömb. Abban az euklideszi térben, amely ugyanarra a bázisra épül, mint a Minkowski-geometria csak a hossznégyzetet euklideszi módon a koordináták négyzetösszegeként származtatjuk, egy kétköpenyű hiperboloid reprezentálja, melynek egyik összefüggő darabját (pl. a felső féltérhez tartozót) szokás a hiperbolikus sík hiperboloid modelljének is nevezni. A hiperboloid modell maximális geodetikusai a beágyazó tér origóján áthaladó síkok által kimetszett teljes görbék, azaz teljes hiperbola ágak. Így az euklideszi tér egységgömbjén létrejövő szférikus geometriával analóg módon származtatott geometria ez a téridő modellen belül.
. A kapott felület így egy modellje a teljes hiperbolikus síknak. Lambert algebrai ötlete a képzetes sugarú gömbröl a Minkowski-térben az egyik legfontosabb felület, a képzetes sugarú egységgömb. Abban az euklideszi térben, amely ugyanarra a bázisra épül, mint a Minkowski-geometria csak a hossznégyzetet euklideszi módon a koordináták négyzetösszegeként származtatjuk, egy kétköpenyű hiperboloid reprezentálja, melynek egyik összefüggő darabját (pl. a felső féltérhez tartozót) szokás a hiperbolikus sík hiperboloid modelljének is nevezni. A hiperboloid modell maximális geodetikusai a beágyazó tér origóján áthaladó síkok által kimetszett teljes görbék, azaz teljes hiperbola ágak. Így az euklideszi tér egységgömbjén létrejövő szférikus geometriával analóg módon származtatott geometria ez a téridő modellen belül.
Az analógiát erősíti a pontpárok távolságát adó formula. Ha a ![]() feltételnek eleget tevő pontok síkján tekintjük az időszerű vektorokat, egy euklideszi síkba ágyazott Cayley–Klein-modell pontjait kapjuk. Két ilyen pont
feltételnek eleget tevő pontok síkján tekintjük az időszerű vektorokat, egy euklideszi síkba ágyazott Cayley–Klein-modell pontjait kapjuk. Két ilyen pont ![]() és
és ![]() hiperbolikus távolsága a már ismertetett formula alapján kiszámítható, használva a
hiperbolikus távolsága a már ismertetett formula alapján kiszámítható, használva a ![]() ,
, ![]() időszerű helyvektorokat és a
időszerű helyvektorokat és a ![]() egyenesen elhelyezkedő
egyenesen elhelyezkedő ![]() ,
, ![]() fényszerű helyvektorokat. A kapott érték az
fényszerű helyvektorokat. A kapott érték az

formula eredménye, ahol ![]() a
a ![]() sík skaláris szorzata. Mivel a
sík skaláris szorzata. Mivel a ![]() ,
, ![]() ,
, ![]() ,
, ![]() vektorok különbségeinek az utolsó koordinátája nulla, a jobb oldal egyenlő a
vektorok különbségeinek az utolsó koordinátája nulla, a jobb oldal egyenlő a

kifejezéssel, amelyben már az indefinit skaláris szorzat szerepel. Legyen ![]() ,
, ![]() azon két pontja a hiperboloid modellnek, melyek centrális vetülete a
azon két pontja a hiperboloid modellnek, melyek centrális vetülete a ![]() síkra az origóból éppen
síkra az origóból éppen ![]() és
és ![]() ;
; ![]() és
és ![]() pedig az a két fényszerű vektor, melyet a
pedig az a két fényszerű vektor, melyet a ![]() egyenes metsz ki a fénykúpból. Ekkor a Papposz–Steiner-tétel szerint ezen utóbbi érték éppen
egyenes metsz ki a fénykúpból. Ekkor a Papposz–Steiner-tétel szerint ezen utóbbi érték éppen
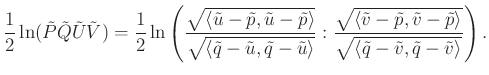
Feltéve, hogy ![]() és
és ![]() , ha felhasználjuk, hogy
, ha felhasználjuk, hogy ![]() és
és ![]() kapjuk, hogy
kapjuk, hogy ![]() , és
, és ![]() ahonnan az együtthatókra az
ahonnan az együtthatókra az
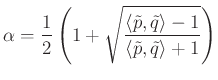 és
és 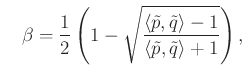
értékek adódnak. Mivel a ![]() kettősviszony egyenlő az
kettősviszony egyenlő az ![]() számmal, és most
számmal, és most ![]() is teljesül kapjuk, hogy
is teljesül kapjuk, hogy
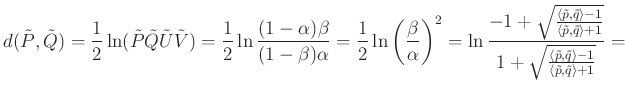
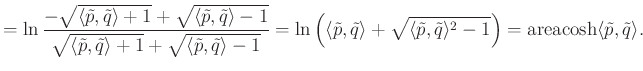
Ha vizsgálatainkat a ![]() metszet Cayley–Klein-modelljére és így az
metszet Cayley–Klein-modelljére és így az ![]() hiperboloid által meghatározott hiperbolikus geometriára végeztük volna, akkor hasonlóképpen a
hiperboloid által meghatározott hiperbolikus geometriára végeztük volna, akkor hasonlóképpen a

formulát kapjuk, mely a szférikus távolságfogalommal mutat pontos egyezést. A hiperbolikus sík modellje mellett a téridő modellben egyéb érdekes geometriák is reprezentálódnak mint alkalmas felület belső geometriája. Tekinthetjük azon pontok halmazát is, melyek helyvektorainak hossznégyzete ![]() . Ennek a halmaznak a pontjai a beágyazó tér egy egyköpenyű hiperboloidját adják, amelynek differenciálgeometriai értelemben vett görbülete
. Ennek a halmaznak a pontjai a beágyazó tér egy egyköpenyű hiperboloidját adják, amelynek differenciálgeometriai értelemben vett görbülete ![]() , azaz a Minkowski-tér pozitív konstans görbületű felületeként jelentkezik. A kapcsolódó geometriát de Sitter-térnek nevezik. A geodetikusok a hiperboloid modellel analóg módon szintén az origón áthaladó síkokkal való hiperbola metszetek. Nem meglepő tehát, hogy a de Sitter-síknak is van egy szép egyszerű modellje a valós projektív síkon. Egy Cayley-Klein-modell komplementerében elhelyezkedő pontok halmaza az alaphalmaz, az egyenesek pedig a projektív egyenesek ezen alaphalmazzal való metszetei. A hiperbolikus és a de Sitter-sík egyaránt származtatható Klein módszerével, ezért ezen geometriák a kilenc Cayley–Klein-féle síkgeometria közül valók.
, azaz a Minkowski-tér pozitív konstans görbületű felületeként jelentkezik. A kapcsolódó geometriát de Sitter-térnek nevezik. A geodetikusok a hiperboloid modellel analóg módon szintén az origón áthaladó síkokkal való hiperbola metszetek. Nem meglepő tehát, hogy a de Sitter-síknak is van egy szép egyszerű modellje a valós projektív síkon. Egy Cayley-Klein-modell komplementerében elhelyezkedő pontok halmaza az alaphalmaz, az egyenesek pedig a projektív egyenesek ezen alaphalmazzal való metszetei. A hiperbolikus és a de Sitter-sík egyaránt származtatható Klein módszerével, ezért ezen geometriák a kilenc Cayley–Klein-féle síkgeometria közül valók.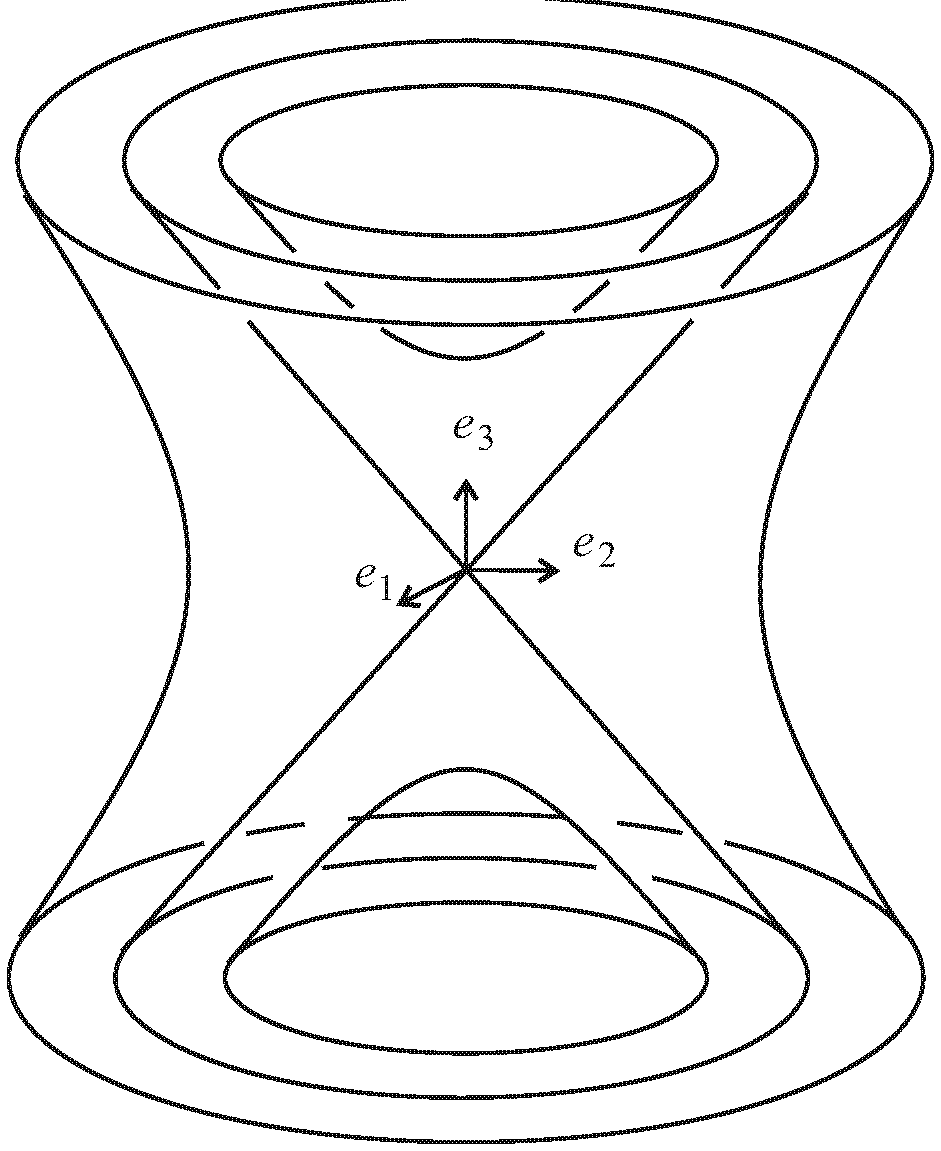
Vegyük észre, hogy a Minkowski-térnek megfeleltetett euklideszi tér egységgömbjének felszíne térszerű, időszerű és fényszerű vektorok végpontjaiból áll, azaz három diszjunkt halmaz egyikéhez sorolhatóak. A tér vektoraira ugyanez áll, hiszen valós számmal való szorzás a vektor jellegét nem változtatja meg. A három halmaz közül a fényszerű vektorok egy konvex kúpot határoznak meg, ez választja el egymástól az időszerű és térszerű vektorok halmazát. Az időszerű vektorok fekszenek ezen konvex kúp belsejében, a térszerűek a külsejében. Az időszerű vektorok „egységgömbje” a hiperbolikus sík, a térszerűeké a de Sitter-sík. A fényszerű vektorok kúpja a fénykúp, ennek az origó szinguláris pontja, de a többi pontban a szorzatgörbület ![]() , így ez a felület az euklideszi sík egy darabjának ábrázolását adja. Az euklideszi tér egységgömbje, mint a téridő modell egy felülete már nem konstans szorzatgörbületű felület.
, így ez a felület az euklideszi sík egy darabjának ábrázolását adja. Az euklideszi tér egységgömbje, mint a téridő modell egy felülete már nem konstans szorzatgörbületű felület.
A normált terek geometriája
Minkowski a geometriai számelmélet körében végzett vizsgálatai során a következő fontos észrevételt teszi: Ha adott egy euklideszi tér és benne egy origó közepű centrálszimmetrikus korlátos és zárt konvex test, akkor a vektorok hosszát mérhetjük relatív módon ehhez a ![]() testhez viszonyítva is. A legkisebb olyan pozitív
testhez viszonyítva is. A legkisebb olyan pozitív ![]() számot kell a vektor hosszának tekinteni, melyre
számot kell a vektor hosszának tekinteni, melyre ![]() tartalmazza a vektor végpontját (a kezdőpont mindig az origó). Igazolja, hogy a
tartalmazza a vektor végpontját (a kezdőpont mindig az origó). Igazolja, hogy a ![]() testhez rendelt ezen
testhez rendelt ezen ![]() függvény rendelkezik az abszolútérték-függvény tulajdonságaival, azaz nem negatív értékeket vesz fel és ha ez nulla, akkor a vizsgált vektor a nullvektor, továbbá pozitív homogén, és szubadditív függvény. (Azaz
függvény rendelkezik az abszolútérték-függvény tulajdonságaival, azaz nem negatív értékeket vesz fel és ha ez nulla, akkor a vizsgált vektor a nullvektor, továbbá pozitív homogén, és szubadditív függvény. (Azaz ![]() és
és ![]() teljesül minden
teljesül minden ![]() ,
, ![]() esetén.) Az olyan vektorteret, amelyen értelmezett egy norma függvény normált térnek nevezzük. A véges dimenziós valós test felett értelmezett vektorterekből származtatott normált tereket geometriai Minkowski-tereknek nevezzük, megkülönböztetve őket a téridőtől. A XX. század matematikájában a normált terek elméletének jelentős szerepe van, a matematika új és termékeny ágait hozta ez a fogalom létre. Cikkünkbe viszont más okból került. Az euklideszi geometriának általánosítását kapjuk így, hiszen ha a
esetén.) Az olyan vektorteret, amelyen értelmezett egy norma függvény normált térnek nevezzük. A véges dimenziós valós test felett értelmezett vektorterekből származtatott normált tereket geometriai Minkowski-tereknek nevezzük, megkülönböztetve őket a téridőtől. A XX. század matematikájában a normált terek elméletének jelentős szerepe van, a matematika új és termékeny ágait hozta ez a fogalom létre. Cikkünkbe viszont más okból került. Az euklideszi geometriának általánosítását kapjuk így, hiszen ha a ![]() egységgömbnek az euklideszi gömböt választjuk, akkor az euklideszi geometria vektorhossz fogalmát jelenti a vektor normája. Ugyanakkor számos olyan gyakorlatban fellépő feladat van, amelynek modellezésére egy másik konvex testhez tartozó távolságmérés megfelelőbb, mint az euklideszi. Ha például kirándulás közben szintkülönbségben szeretnénk jegyezni teljesítményünket, gyorsabban növeljük azt (ugyanazon gyaloglási sebesség mellett) ha a szintvonalakra merőlegesen haladunk, mintha egy szintvonalon. A szintvonalakat nagyjából koncentrikus konvex halmazoknak tekintve és egy ilyet egységgömbnek választva, a Minkowski-hossz kalkulálásának segítségével határozhatjuk meg teljesítményünket.
egységgömbnek az euklideszi gömböt választjuk, akkor az euklideszi geometria vektorhossz fogalmát jelenti a vektor normája. Ugyanakkor számos olyan gyakorlatban fellépő feladat van, amelynek modellezésére egy másik konvex testhez tartozó távolságmérés megfelelőbb, mint az euklideszi. Ha például kirándulás közben szintkülönbségben szeretnénk jegyezni teljesítményünket, gyorsabban növeljük azt (ugyanazon gyaloglási sebesség mellett) ha a szintvonalakra merőlegesen haladunk, mintha egy szintvonalon. A szintvonalakat nagyjából koncentrikus konvex halmazoknak tekintve és egy ilyet egységgömbnek választva, a Minkowski-hossz kalkulálásának segítségével határozhatjuk meg teljesítményünket.
Ezen geometria is megfelel a korábbi differenciálgeometriai elvárásainknak, ha az egységgömb alakjára további megszorításokat teszünk, de létrehozhatók olyan geometriák is, amelyek nem a fizikai térfogalom fejlődéséhez járulnak hozzá, hanem a tudomány más területeit segítik. Poliédrikus Minkowski-térnek nevezzük az olyan geometriai Minkowski-teret, melynek egységgömbje poliéder. Két fontos ilyen tér a kocka és a szabályos oktaéder egységgömbbel rendelkező terek, melyek a háromdimenziós ![]() illetve
illetve ![]() tereknek felelnek meg. Minden
tereknek felelnek meg. Minden ![]() esetén az
esetén az ![]() tér is egy Minkowski-tér, közűlük az
tér is egy Minkowski-tér, közűlük az ![]() felel meg az euklideszi térnek.
felel meg az euklideszi térnek.
Visszatérve a világ lehetséges leírásaira, ugyanúgy mint a fizikai, a geometriai Minkowski-tér is származtatható a skaláris szorzat alkalmas általánosítása útján. Ez az általánosítás a félskaláris szorzat függvény. Láttuk, hogy a skaláris szorzat függvény fontos tulajdonsága, hogy teljesíti a Cauchy–-Schwarz–Bunyakovszkij-egyenlőtlenséget. Definiáljuk a félskaláris szorzatot egy olyan a vektorpárok halmazából a valós számok halmazába képező ![]() függvényként, mely pozitív definit (
függvényként, mely pozitív definit ( ![]() és egyenlőség csak a nullvektor esetén áll fenn), az első változójában lineáris, a másodikban homogén (azaz
és egyenlőség csak a nullvektor esetén áll fenn), az első változójában lineáris, a másodikban homogén (azaz ![]() ) és tetszőleges vektorpárra teljesíti a Cauchy–Schwarz–Bunyakovszkij-egyenlőtlenséget (azaz
) és tetszőleges vektorpárra teljesíti a Cauchy–Schwarz–Bunyakovszkij-egyenlőtlenséget (azaz ![]() ). Igazolható, hogy tetszőleges normához megadható olyan félskaláris szorzat, mely alapján történő hossznégyzet számítás az adott norma négyzetére vonatkozó értéket adja vissza. Ez alapján a félskaláris szorzat és a norma közötti kapcsolat megfelel a skaláris szorzat és az euklideszi hossz, vagy az indefinit skaláris szorzat és a téridő metrikájára vonatkozó hossz között fellépő kapcsolatoknak. A félskaláris szorzat bevezetése Lumer érdeme ([13]), aki funkcionálanalízisbeli vizsgálataihoz keresett alkalmas, a Hilbert-terek skaláris szorzatának megfelelő apparátust.
). Igazolható, hogy tetszőleges normához megadható olyan félskaláris szorzat, mely alapján történő hossznégyzet számítás az adott norma négyzetére vonatkozó értéket adja vissza. Ez alapján a félskaláris szorzat és a norma közötti kapcsolat megfelel a skaláris szorzat és az euklideszi hossz, vagy az indefinit skaláris szorzat és a téridő metrikájára vonatkozó hossz között fellépő kapcsolatoknak. A félskaláris szorzat bevezetése Lumer érdeme ([13]), aki funkcionálanalízisbeli vizsgálataihoz keresett alkalmas, a Hilbert-terek skaláris szorzatának megfelelő apparátust.
Utószó
Írásunkban láthatóan a XIX. század nagy matematikusainak tevékenységéhez kapcsolható geometriai térfogalmak szerepeltek. Ne vezessen ez minket tévútra ezen fogalmak korszerűségének a dolgában. Annak ellenére, hogy jelenleg a XXI. századot írjuk, ezen térfogalmak semmit sem koptak, valamennyi – a modern tudományban jelenleg használt – a fizikai világról szóló leírás kiindulási pontja a fent leírt geometriák egyike. A differenciálgeometriai vizsgálatok zömében speciális Riemann-, Finsler- vagy szemi-Riemann-terekben zajlanak. Az első tér pontjainak érintő terein skaláris szorzat által indukált euklideszi teret feltételezünk, a második érintőterein félskaláris szorzat által indukált norma adja a metrikát, míg a harmadik érintőterei indefinit skaláris szorzat által indukált pseudo-euklideszi terek (olyan fizikai Minkowski-terek, melyek szignatúrája esetleg különbözik a téridőétől).
A fizikai világhoz kapcsolt kutatások olyan Lorentz-sokaságokra vonatkoznak, melyek ![]() -dimenzíós szemi-Riemann-sokaságok, téridö modellet adó geometriával az érintőtereiken. Még egy ilyen általános térfogalom is épülhet konkrét módon valamelyik fentebb említett geometriára. Az általános relativitás elméletének sarokköve Einstein azon egyenlete, mely egy ismeretlennek tekintett geometria Ricci-görbületét, skalárgörbületét és metrikus alaptenzorát kapcsolja össze a fizikai adatokat magában foglaló energiaimpulzus tenzorral. Az Einstein-egyenlet megoldása nehéz feladat, ennek ellenére számos megoldását ismerjük (az első Schwartschildtól származik). Közűlük egy a Robertson–Walker-féle téridő, mely szerkezetét tekintve olyan mint a téridő modell, avval a különbséggel, hogy egy fix koordináta-rendszer időtengelye abszolút időnek van kijelölve és az egy abszolút időpillanatban zajló események
-dimenzíós szemi-Riemann-sokaságok, téridö modellet adó geometriával az érintőtereiken. Még egy ilyen általános térfogalom is épülhet konkrét módon valamelyik fentebb említett geometriára. Az általános relativitás elméletének sarokköve Einstein azon egyenlete, mely egy ismeretlennek tekintett geometria Ricci-görbületét, skalárgörbületét és metrikus alaptenzorát kapcsolja össze a fizikai adatokat magában foglaló energiaimpulzus tenzorral. Az Einstein-egyenlet megoldása nehéz feladat, ennek ellenére számos megoldását ismerjük (az első Schwartschildtól származik). Közűlük egy a Robertson–Walker-féle téridő, mely szerkezetét tekintve olyan mint a téridő modell, avval a különbséggel, hogy egy fix koordináta-rendszer időtengelye abszolút időnek van kijelölve és az egy abszolút időpillanatban zajló események ![]() -dimenziós tere pedig egy konstans
-dimenziós tere pedig egy konstans ![]() görbületű tér, ahol
görbületű tér, ahol ![]() egy fix
egy fix ![]() -dimenziós konstans görbületű tér görbülete. (A
-dimenziós konstans görbületű tér görbülete. (A ![]() függvényt nevezik görbítő függvénynek.) Ha visszafelé haladunk az időben, e szerint a modell szerint a térszerű metszeteknek egyre jobban kell görbülniük (ha feltesszük, hogy
függvényt nevezik görbítő függvénynek.) Ha visszafelé haladunk az időben, e szerint a modell szerint a térszerű metszeteknek egyre jobban kell görbülniük (ha feltesszük, hogy ![]() ), ami az ősrobbanás elméletéhez vezet. Az újabb mérési eredményekkel azonban csak olyan Robertson–Walker-téridő lehet összhangban, melyben a
), ami az ősrobbanás elméletéhez vezet. Az újabb mérési eredményekkel azonban csak olyan Robertson–Walker-téridő lehet összhangban, melyben a ![]() görbület negatív. Ha ez a modell tükrözi világunkat a legjobban, akkor a hiperbolikus geometriának a fizikai számításainkban jelentős szerepe kell legyen.
görbület negatív. Ha ez a modell tükrözi világunkat a legjobban, akkor a hiperbolikus geometriának a fizikai számításainkban jelentős szerepe kell legyen.
G. Horváth Ákos
Irodalomjegyzék
- 1
- Bolyai-emlékkönyv, Vince Kiadó, Budapest, 2004.
2- Bolyai, J.: Appendix Akadémiai Kiadó, Budapest, 1952.
3- Beltrami, E.: Saggio di interpretatione della geometria non euclidea. Giornale di Mathematiche, 6 (1869), 284-312.
4- Casey, J.: A treatise on Spherical Trigonometry, and its application to Geodesy and Astronomy, with numerous examples, Hodges, Figgis and CO., Grafton-ST. London: Longmans, Green, and CO., 1889.
5- Eukleidész: Elemek Gondolat, Budapest, 1983.
6- Abardia J., Reventós, A., Rodrigúes, C.J.: What did Gauss read in the Appendix? Historia Mathematica 39/3, 292-323.
7- Grassmann, H. G.: Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert, O. Wigand, Leipzig, 1844.
8- G.Horváth, Á.: Csodálatos geometria, Typotex, 2013.
9- G.Horváth, Á, Szirmai, J.: A nemeuklideszi geometriák modelljei, Typotex, 2003.
10- Gray, J.: Non-Euclidean geometry - a Re-interpretation. Historia Mathematica 6 (1979), 236-258.
11- Hamilton, W. R.: On quaternions or a new system of imaginaries in algebra. Philosophical Magazine, (1844 to 1850)
12- Lambert, J. H.: Theorie der Parallellinien Mag. Reine Angew. Math. (1786), 137–164, 325–358.
13- Lumer, G.: Semi-inner product spaces. Trans. Amer. Math. Soc. 100 (1961), 29-43.
14- Minkowski, H.: Raum und Zeit Jahresberichte der Deutschen Mathematiker-Vereinigung, Leipzig, 1909.
15- Salmon, G.: A treatise on the analytic geometry of three dimension. (Fourth Edition) Hodges, Figgis and Co., 1882.
16- Szász, P.: Bevezetés a Bolyai-Lobacsevszkij-féle geometriába. Akadémiai Kiadó, Budapest, 1973.
17- van der Waerden, B. L.: Egy tudomány ébredése. Gondolat, Budapest, 1977.









