A pszeudo-holomorf (vagy
A pszeudo-holomorf (vagy ![]() -holomorf) görbe fogalmát Gromov vezette be 1986-ban, amivel gyökeresen alakította át a szimplektikus topológiát, és több más közeli diszciplínára, például algebrai geometriára, húrelméletre, 4-sokaságok elméletére volt döntő hatással; ezekre később még visszatérünk.
-holomorf) görbe fogalmát Gromov vezette be 1986-ban, amivel gyökeresen alakította át a szimplektikus topológiát, és több más közeli diszciplínára, például algebrai geometriára, húrelméletre, 4-sokaságok elméletére volt döntő hatással; ezekre később még visszatérünk.
A „görbe” – mondjuk egy síkgörbe – mindannyiunk számára ismerős fogalom. Két módon is megadhatunk egy síkgörbét: akár mint az ![]() egyenlet megoldáshalmazát valamilyen
egyenlet megoldáshalmazát valamilyen ![]() függvényre, akár az
függvényre, akár az ![]() paraméterezéssel. A körvonalat például megadhatjuk az
paraméterezéssel. A körvonalat például megadhatjuk az ![]() egyenlettel vagy az
egyenlettel vagy az ![]() paraméterezéssel. Egy további ismerős fogalom görbék egy „családja”, például a sík összes egyeneseinek családja.
paraméterezéssel. Egy további ismerős fogalom görbék egy „családja”, például a sík összes egyeneseinek családja.
Görbéket mind a differenciálgeometriában, mind az algebrai geometriában hosszú ideje tanulmányoznak. A klasszikus elmélet számunkra most érdekes változata a „komplex” vagy „holomorf” görbék elmélete. Legegyszerűbb változatában helyettesítsük az ![]() valós változókat a
valós változókat a ![]() komplex változókkal; így egy komplex görbét kapunk a komplex síkon. A
komplex változókkal; így egy komplex görbét kapunk a komplex síkon. A ![]() egyenlet például egy komplex görbét ad meg. Hasonlóan, tekinthetünk paraméterezett komplex görbéket, melyeket a
egyenlet például egy komplex görbét ad meg. Hasonlóan, tekinthetünk paraméterezett komplex görbéket, melyeket a ![]() egyenletek adnak meg, ahol
egyenletek adnak meg, ahol ![]() és
és ![]() holomorf függvényei a
holomorf függvényei a ![]() komplex változónak. Általánosabban, komplex sokaságokban is tekinthetünk komplex görbéket, melyeket Riemann-sokaságokon értelmezett holomorf függvények parametrizálnak.
komplex változónak. Általánosabban, komplex sokaságokban is tekinthetünk komplex görbéket, melyeket Riemann-sokaságokon értelmezett holomorf függvények parametrizálnak.
De mi is egy holomorf leképezés? Vegyük először a legegyszerűbb esetet, amikor az ![]() leképezés
leképezés ![]() -ből
-ből ![]() -be képez: ekkor egyszerűen egy holomorf függvény. A holomorf tulajdonságot a Cauchy-Riemann egyenlet teljesülése jelenti, vagyis hogy
-be képez: ekkor egyszerűen egy holomorf függvény. A holomorf tulajdonságot a Cauchy-Riemann egyenlet teljesülése jelenti, vagyis hogy
![]() Az egyenlet azt fejezi ki, hogy az
Az egyenlet azt fejezi ki, hogy az ![]() deriváltja (többváltozós függvénytani értelmében) minden pontban egy
deriváltja (többváltozós függvénytani értelmében) minden pontban egy ![]() -ből
-ből ![]() -be vezető komplex lineáris leképezés. A fogalom természetesen terjed ki majdnem-komplex sokaságokra is. Legyen tehát
-be vezető komplex lineáris leképezés. A fogalom természetesen terjed ki majdnem-komplex sokaságokra is. Legyen tehát ![]() egy
egy ![]() -dimenziós differenciálható (vagy más néven sima) sokaság. Egy
-dimenziós differenciálható (vagy más néven sima) sokaság. Egy ![]() -en értelmezett majdnem-komplex struktúra egy
-en értelmezett majdnem-komplex struktúra egy ![]() leképezés-család mely minden
leképezés-család mely minden ![]() pontra a
pontra a ![]() érintőtéren teljesíti a
érintőtéren teljesíti a ![]() egyenletet, és
egyenletet, és ![]() -től differenciálható módon függ. Röviden,
-től differenciálható módon függ. Röviden, ![]() az érintőtereket komplex vektorterekké teszi. Minden komplex sokaságon van egy természetes majdnem-komplex struktúra, de a megfordított állítás már nem igaz
az érintőtereket komplex vektorterekké teszi. Minden komplex sokaságon van egy természetes majdnem-komplex struktúra, de a megfordított állítás már nem igaz ![]() esetén: egy integrálhatósági feltétel karakterizálja azokat a speciális majdnem-komplex struktúrákat, melyek komplex struktúrából származnak. Számos olyan sokaság létezik, melyen ugyan van majdnem-komplex struktúra, de egyáltalán nem látható el komplex struktúrával.
esetén: egy integrálhatósági feltétel karakterizálja azokat a speciális majdnem-komplex struktúrákat, melyek komplex struktúrából származnak. Számos olyan sokaság létezik, melyen ugyan van majdnem-komplex struktúra, de egyáltalán nem látható el komplex struktúrával.
A pszeudo-holomorf görbe fogalma a holomorf görbe természetes módosítása arra az esetre, amikor a bennfoglaló sokaság csak majdnem-komplex. Pontosabban, vegyünk egy ![]() Riemann-felületet, egy
Riemann-felületet, egy ![]() majdnem-komplex sokaságot és egy
majdnem-komplex sokaságot és egy ![]() differenciálható leképezést melyre minden
differenciálható leképezést melyre minden ![]() esetén teljesül, hogy a
esetén teljesül, hogy a![]() derivált leképezés komplex lineáris az adott komplex struktúrákkal az érintőtereken. Konkrétan, tekintsük a
derivált leképezés komplex lineáris az adott komplex struktúrákkal az érintőtereken. Konkrétan, tekintsük a ![]() ,
, ![]() és ezen egy
és ezen egy ![]() általános majdnem-komplex struktúra esetét. Lineáris algebrai érveléssel látható, hogy az
általános majdnem-komplex struktúra esetét. Lineáris algebrai érveléssel látható, hogy az ![]() -lineáris
-lineáris ![]() leképezések melyek a
leképezések melyek a ![]() egyenletet is teljesítik, az
egyenletet is teljesítik, az ![]() -es komplex mátrixok (melyeket
-es komplex mátrixok (melyeket ![]() -val jelölünk) egy nyílt részhalmazát alkotják. A majdnem-komplex struktúra tehát egy
-val jelölünk) egy nyílt részhalmazát alkotják. A majdnem-komplex struktúra tehát egy ![]() (
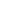
( ![]() ) mátrix-értékű függvénnyel írható le. Egy pszeudo-holomorf görbe a következő parciális differenciálegyenlet megoldásaként adható meg:
) mátrix-értékű függvénnyel írható le. Egy pszeudo-holomorf görbe a következő parciális differenciálegyenlet megoldásaként adható meg:
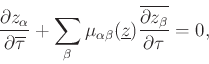 az egyenlet a szokásos Cauchy-Riemann egyenlet deformációjának tekinthető a
az egyenlet a szokásos Cauchy-Riemann egyenlet deformációjának tekinthető a ![]() vektorértékű függvényre.
vektorértékű függvényre.
Azzal, hogy majdnem-komplex struktúrákat tekintünk, a klasszikus holomorf görbe-elméletnél szélesebb és rugalmasabb világban találjuk magunkat. A klasszikus elmélet számos vetülete nem nagyon változik, amennyiben ilyen irányba terjesztjük azt ki. Röviden azt mondhatjuk, hogy a pszeudo-holomorf görbék lokális elmélete nagyon hasonlít a holomorf görbék elméletéhez. Ebben a kontextusban a lokálisnak két értelmezése is lehetséges: akár úgy, hogy a problémát lokálisan vizsgáljuk az ![]() sokaságban vagy lokálisan a leképezések terében. Fontos kiemelni, hogy görbéket vizsgálunk és nem magasabb dimenziós objektumokat. Ugyan bármely
sokaságban vagy lokálisan a leképezések terében. Fontos kiemelni, hogy görbéket vizsgálunk és nem magasabb dimenziós objektumokat. Ugyan bármely ![]() majdnem-komplex sokaság-párra értelmezhető egy
majdnem-komplex sokaság-párra értelmezhető egy ![]() leképezés (pszeudo-)holomorfsága, de amint
leképezés (pszeudo-)holomorfsága, de amint ![]() valós dimenziója több mint 2, ez nem túl hasznos fogalom. Egy általános majdnem-komplex
valós dimenziója több mint 2, ez nem túl hasznos fogalom. Egy általános majdnem-komplex ![]() sokaság esetén, melynek dimenziója több mint 2, például még lokálisan sem létezik nem-konstans (pszeudo)holomorf leképezés
sokaság esetén, melynek dimenziója több mint 2, például még lokálisan sem létezik nem-konstans (pszeudo)holomorf leképezés ![]() -be – épp ez az integrálhatósági feltétel forrása komplex sokaságokra.
-be – épp ez az integrálhatósági feltétel forrása komplex sokaságokra.
Állításunk egy pontosabb megfogalmazása a következő: egy ![]() kompakt Riemann-sokaság esetén egy adott
kompakt Riemann-sokaság esetén egy adott ![]() pszeudo-holomorf görbe deformációinak elméletét egy nem-lineáris Fredholm-elmélet írja le. Ez nagyjából azt jelenti, hogy a deformációkat egy véges dimenziós sokaság, egy
pszeudo-holomorf görbe deformációinak elméletét egy nem-lineáris Fredholm-elmélet írja le. Ez nagyjából azt jelenti, hogy a deformációkat egy véges dimenziós sokaság, egy ![]() modulustér paraméterezi, melynek dimenzióját topológikus adatokból lehet kiszámolni. Továbbá ez a modulustér simán változik mind a
modulustér paraméterezi, melynek dimenzióját topológikus adatokból lehet kiszámolni. Továbbá ez a modulustér simán változik mind a ![]() majdnem-komplex struktúra mind a
majdnem-komplex struktúra mind a ![]() -n rögzített Riemann-sokaság struktúra függvényeként. Vegyük például azt az esetet, amikor
-n rögzített Riemann-sokaság struktúra függvényeként. Vegyük például azt az esetet, amikor ![]() a komplex projektív tér (annak standard komplex struktúrájával),
a komplex projektív tér (annak standard komplex struktúrájával), ![]() pedig a Riemann-gömb. Ekkor minden
pedig a Riemann-gömb. Ekkor minden ![]() -beli „egyenes” (a szó projektív geometriai értelmében) valamint egy egyenes minden paraméterezése egy pszeudo-holomorf görbét ad. Következésképp az
-beli „egyenes” (a szó projektív geometriai értelmében) valamint egy egyenes minden paraméterezése egy pszeudo-holomorf görbét ad. Következésképp az ![]() modulustér a duális sík felett egy
modulustér a duális sík felett egy ![]() -fibrumú nyaláb (a
-fibrumú nyaláb (a ![]() csoport a Möbius-leképezések csoportja). A nem-lineáris Fredholm-elmélet azt mutatja, hogy ha deformáljuk a majdnem-komplex struktúrát, akkor ugyan valószínűleg nem tudjuk majd a pszeudo-holomorf görbéket expliciten leírni, de hasonló általános tulajdonságokkal rendelkező modulusteret kapunk.
csoport a Möbius-leképezések csoportja). A nem-lineáris Fredholm-elmélet azt mutatja, hogy ha deformáljuk a majdnem-komplex struktúrát, akkor ugyan valószínűleg nem tudjuk majd a pszeudo-holomorf görbéket expliciten leírni, de hasonló általános tulajdonságokkal rendelkező modulusteret kapunk.
Gromov észrevétele az volt, hogy a Fredholm elmélet által a pszeudo-holomorf leképezésekről adott lokális kép egy globális képpé alakítható, feltéve hogy ![]() majdnem-komplex struktúrája egy szimplektikus struktúrával kompatibilis. Emlekézzünk, hogy egy szimplektikus struktúrát egy olyan
majdnem-komplex struktúrája egy szimplektikus struktúrával kompatibilis. Emlekézzünk, hogy egy szimplektikus struktúrát egy olyan ![]() külső 2-forma ad meg, mely két feltételt teljesít. Az első feltétel pontonkénti és algebrai: a sokaság minden pontjában
külső 2-forma ad meg, mely két feltételt teljesít. Az első feltétel pontonkénti és algebrai: a sokaság minden pontjában ![]() egy nem-elfajuló anti-szimmetrikus forma
egy nem-elfajuló anti-szimmetrikus forma ![]() abban a pontban vett érintőterén. A másik feltétel globálisabb és differenciálgeometriai: az
abban a pontban vett érintőterén. A másik feltétel globálisabb és differenciálgeometriai: az ![]() 2-forma zárt. Akkor mondjuk, hogy
2-forma zárt. Akkor mondjuk, hogy ![]() kompatibilis
kompatibilis ![]() -val, ha az érintővektorokon értelmezett
-val, ha az érintővektorokon értelmezett
![]() bilineáris forma szimmetrikus és pozitív definit. Ebben az esetben
bilineáris forma szimmetrikus és pozitív definit. Ebben az esetben ![]() egy
egy ![]() -en értelezett Riemann metrika lesz. Legyen
-en értelezett Riemann metrika lesz. Legyen ![]() egy pszeudo-holomorf leképezés. Az
egy pszeudo-holomorf leképezés. Az
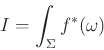 integrálra ekkor kétféleképp is gondolhatunk. Egyrészt, a pontonkénti kompatibilitás miatt
integrálra ekkor kétféleképp is gondolhatunk. Egyrészt, a pontonkénti kompatibilitás miatt ![]() lényegében az
lényegében az ![]() képének területe, melyet a
képének területe, melyet a ![]() metrika segítségével mérünk. Másrészt viszont, mivel
metrika segítségével mérünk. Másrészt viszont, mivel ![]() zárt forma, az
zárt forma, az ![]() mennyiség az
mennyiség az ![]() leképezés topologikus (homotopikus) invariánsa. Következésképp ebben az esetben pszeudo-holomorf görbék területe egy egyszerű topologikus adattal határozható meg. Ezt a tulajdonságot használva Gromov egy részleges kompaktsági tulajdonságot tudott bizonyítani a modulusterekre. Vegyük például a Riemann gömbről a komplex projektív síkba mutató leképezéseket. Ha megengedjük, hogy a majdnem-komplex struktúrát tetszőleges mértékben és tetszőleges irányban deformáljuk, akkor nem sokat tudunk mondani, hiszen a pszeudo-holomorf görbék nagyon bonyolult módokon degenerálódhatnak ahogy a majdnem-komplex struktúrát deformájuk, és a leképezések akár el is „tűnhetnek”. De ha csak olyan majdnem-komplex struktúrákat engedünk meg, melyek egy szimplektikus formával kompatibilisek, akkor a görbék nem tudnak degenerálódni, mert területüket kontrollálni tudjuk. Ebben az esetben Gromov valójában megmutatta, hogy a görbéknek meg kell maradniuk, akármilyen nagy deformációt is alkalmazunk.
leképezés topologikus (homotopikus) invariánsa. Következésképp ebben az esetben pszeudo-holomorf görbék területe egy egyszerű topologikus adattal határozható meg. Ezt a tulajdonságot használva Gromov egy részleges kompaktsági tulajdonságot tudott bizonyítani a modulusterekre. Vegyük például a Riemann gömbről a komplex projektív síkba mutató leképezéseket. Ha megengedjük, hogy a majdnem-komplex struktúrát tetszőleges mértékben és tetszőleges irányban deformáljuk, akkor nem sokat tudunk mondani, hiszen a pszeudo-holomorf görbék nagyon bonyolult módokon degenerálódhatnak ahogy a majdnem-komplex struktúrát deformájuk, és a leképezések akár el is „tűnhetnek”. De ha csak olyan majdnem-komplex struktúrákat engedünk meg, melyek egy szimplektikus formával kompatibilisek, akkor a görbék nem tudnak degenerálódni, mert területüket kontrollálni tudjuk. Ebben az esetben Gromov valójában megmutatta, hogy a görbéknek meg kell maradniuk, akármilyen nagy deformációt is alkalmazunk.
E két tulajdonság – a Fredholm elmélet és a kompaktság – adja Gromov elméletének alapjait, mely keretében pszeudo-holomorf görbéket használunk szimplektikus topológiai kérdések megválaszolására. Ezeket a görbéket két alapvető módon használhatjuk. Az első megközelítésben mint geometrikus ‚szondákat’, melyekkel felderíthető a szimplektikus sokaság: például Gromov egy eredménye szerint (melyet később Taubes terjesztett ki) a komplex projektív síkon egyetlen szimplektikus struktúra létezik, melyet úgy lehet belátni, hogy a sokaságot végigseperjük „egyenesekkel” (vagyis olyan pszeudo-holomorf görbékkel, melyeknek ugyanolyan topologikus tulajdonságaik vannak, mint az egyeneseknek a standard esetben). A második megközelítésben a görbék numerikus invariánsok forrásai: ezek az úgynevezett Gromov-Witten invariánsok. A legegyszerűbb esetben, amikor a modulustér 0-dimenziós és véges sok pontból áll, egy egész értékű invariánst kapunk pusztán ezen pontok megszámolásával. E második irány fejlődött legdinamikusabban Gromov cikkének megjelenése után. A Floer homológiák elmélete is hasonló alapokon nyugszik; ebben az esetben olyan pszeudo-holomorf görbéket kell számolni, melyek pereme egy rögzített Lagrange féle részsokaságra képződik. Ez az elmélet vezet el a Fukaya kategória fogalmához. A négydimenziós esetben Taubes felfedezte, hogy a Gromov-Witten invariánsok megegyeznek a Seiberg-Witten invariánsokkal, melyeket teljesen más módon definiálhatunk. Abban az esetben, amikor a sokaság valójában komplex, mondjuk egy algebrai varietás, az invariánsok az algebrai geometria klasszikus leszámlálási kérdéseihez kapcsolódnak. Ugyanezen invariánsok, a Feynman integrálokon keresztül, feltűnnek a topologikus húrelméletben is. Ez a megközelítés teljesen új látásmódot, és csodálatos és érzékeny algebrai struktúrákat, kvantum kohomológiákat eredményezett. A sokaság Fukaya kategóriája pedig, Kontsevich munkája nyomán, a tükörszimmetria jelenségéhez is szorosan kapcsolódik.
Irodalom:
Dusa McDuff és Dietmar Salamon, ![]() -holomorphic Curves and Symplectic Topology, Amer. Math. Soc. Colloq. Publ., Vol. 52, 2004.
-holomorphic Curves and Symplectic Topology, Amer. Math. Soc. Colloq. Publ., Vol. 52, 2004.
______________________________
 Simon Donaldson az Imperial College (London) Royal Society Research professzora. A cikk eredetileg az American Mathematical Society Notices folyóiratának 2005. októberi számában jelent meg a What is …? rovatban. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. A fordítást Stipsicz András készítette.
Simon Donaldson az Imperial College (London) Royal Society Research professzora. A cikk eredetileg az American Mathematical Society Notices folyóiratának 2005. októberi számában jelent meg a What is …? rovatban. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. A fordítást Stipsicz András készítette.
Simon K. Donaldson, “What is…a Pseudoholomorphic Curve?” Notices Amer. Math. Soc., 52 (October 2005) 1026-1027. © 2005 American Mathematical Society.
A cikk bevezető ábráján látható pszeudo-holomorf görbe lelőhelye: https://www.mathematik.hu-