Babai és a gráf-izomorfizmus probléma

Gráfnak nevezünk egy olyan $X$ struktúrát, ahol adott a pontok egy $V$ halmaza, valamint élek (azaz pont-párok) egy $E$ halmaza. A gyakorlatban előforduló véges gráfok közül az egyik legismertebb a Facebook-gráf (itt az élek a Facebook ismerősök között futnak).

A gráf-izomorfizmus probléma (röviden IZO) a következő számitási feladat: Döntsük el, hogy két adott véges gráf, $G$ és $H$ valójában ugyanaz-e, még akkor is, amikor máshogy néznek ki. Azaz döntsük el, hogy van-e olyan bijekció a csúcshalmazok között, amely megőrzi az éleket. Általánosabban azt is vizsgálhatjuk, hogy két adott kombinatorikus struktúra valójában ugyanaz-e. Számos ilyen jellegű probléma visszavezethető az IZO problémára.

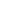
Ez egy olyan, egyszerűen megfogalmazható probléma, amit rendkivül nehéz megoldani. Például, mint az alábbi ábra mutatja, a Petersen gráfot is nagyon különböző módokon lehet ábrázolni.

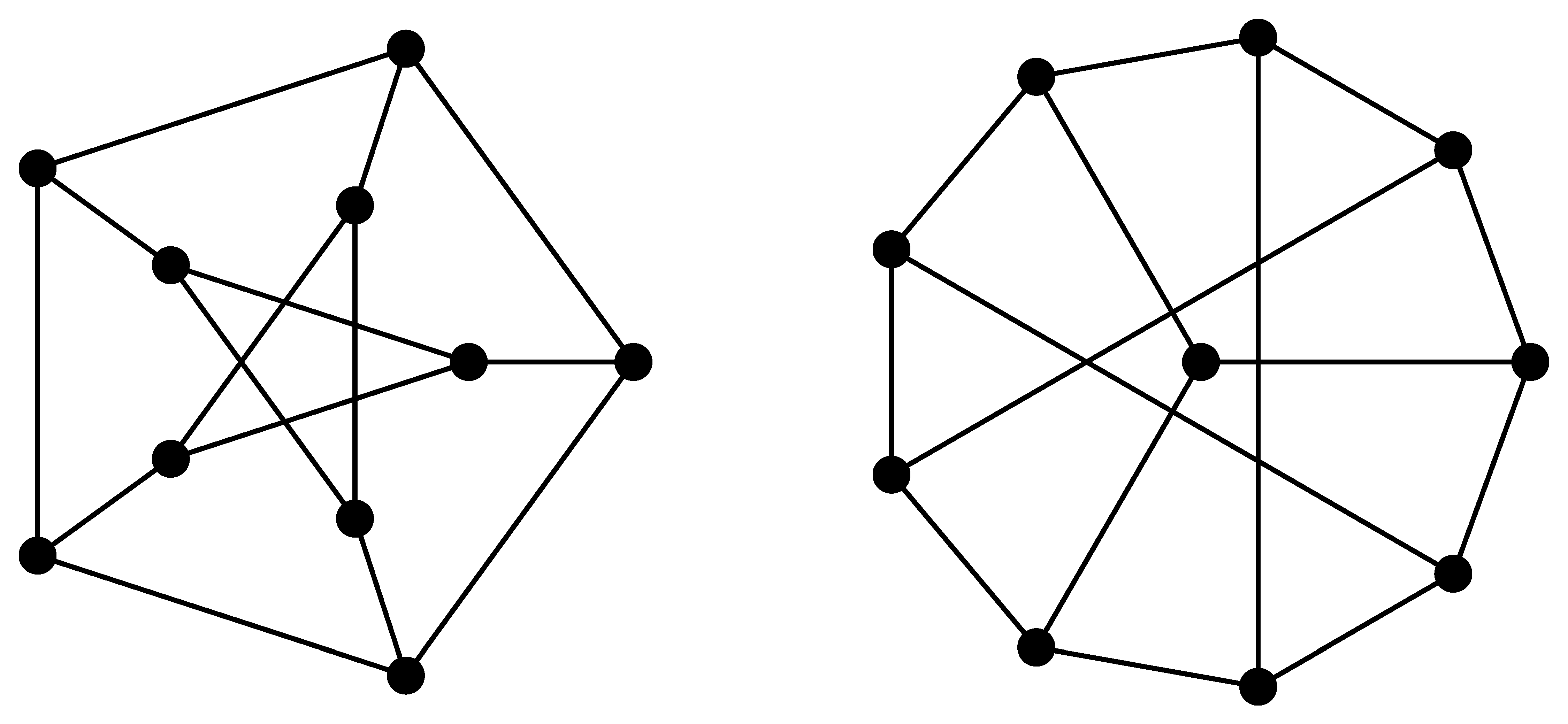
A fenti ábrán 10 pontú gráfok szerepelnek. Képzeljük el, milyen nehéz lehet eldönteni, hogy két $10^{100}$ pontú gráf izomorf-e. Nyilvánvaló, hogy egy ilyen problémát csak nagyteljesítményű géppel lehet megoldani. És még egy ilyen számítógépet használva is valamilyen nagyon gyors algoritmusra van szükségünk. A probléma elméleti jellegű. Léteznek ravasz eljárások arra, hogy mondjuk $10^{10}$ -nél kevesebb pontú gráfokat megkülönböztessünk egymástól [1].

Babai László 2015 novemberében egy háromrészes chicagoi előadássorozatában jelentette be, hogy kvázipolinomiális algoritmust talált az IZO probléma megoldására. (Egy algoritmust kvázipolinomiálisnak nevezünk, ha futási ideje $\exp((\log n)^c)$ , ahol $n$ a vizsgált gráfok pontszáma és $c$ egy abszolút konstans. Például $c=2$ esetén $n^{\log n}$ ami egy kicsivel rosszabb mint $n^k$ ami polinomiális). Ezt az eredményt a matematikus társadalom mint az évtized legnagyobb számítógéptudományi áttörését ünnepelte. Babai bizonyítását egy 90 oldalas kézirat formájában [2] az arxiv.org oldalon tette közzé. Nyilvánvaló, hogy egy ilyen bonyolultságú bizonyítás ellenőrzése sokáig tart. Többen olvastak részeket a kéziratból és kisebb, gyorsan javítható hibákat találtak.

Harald Helfgottot felkérték, hogy a nevezetes Bourbaki-szemináriumon tartson előadást Babai eredményéről. Több hónapos ellenőrző munka után Helfgott szilveszter éjjelén komoly hibát talált. Ezt Babai egy hét intenziv munkával kijavította, egyben egyszerűsitve a bizonyítást. Paradox módon mindez lényegesen növeli az eredmény elfogadottságát. Részben azért, mert Helfgott időközben megtartott párizsi előadásán határozottan kijelentette, hogy a módosított bizonyítás már jó. Mindezekről további információ és a javitás részletes leirása Babai honlapján, illetve Helfgott áttekintő cikkében [3] található.

Miért olyan fontos Babai eredménye? Mert ezzel a megoldással mélyebben megérthetjük a számítógéptudomány lényegét. A gráf-izomorfizmus probléma algoritmikus bonyolultsága az algoritmuselmélet egy, már Cook 1971-es klasszikus dolgozatában [4] is említett nyitott problémája. Ez a probléma különleges szerepet játszik az algoritmuselméletben. A legtöbb ismert, eldöntendő (igen-nem választ váró) probléma vagy a könnyű, azaz polinomiális időben megoldható vagy a nehéz, úgynevezett NP-teljes problémák közé tartozik. Ezekből a nehéz problémákból több ezret ismerünk, az egyik legismertebb annak eldöntése, hogy van-e egy gráfban Hamilton kör, azaz egy olyan kör amely a gráf minden pontján áthalad.

Ahhoz, hogy a fentieket jobban megértsük, néhány alapvető fogalommal kell megismerkednünk az algoritmikus bonyolultság elméletéből. A matematikában, illetve az elméleti számítógéptudományban egy algoritmus hatékonyságát az összes lehetséges inputot vizsgálva becsüljük. Azaz egy IZO algoritmus futási ideje a leghosszabb futási idő az összes lehetséges $n$ pontú $G$ és $H$ gráf-párra. Egy problémát NP-belinek nevezünk ha polinomidőben megoldható egy nemdeterminisztikus Turing gépen. Informálisan, ha bármely valahogyan megtalált megoldásról (mint például egy gráfban egy Hamilton kör vagy a $G$ és $H$ gráfok között megadott izomorfizmus) polinomidőben ellenőrizhető, hogy valóban megoldás-e.

Meglepő módon az NP osztályban léteznek legnehezebb problémák, ezeket nevezzük NP-teljesnek. Bármelyik NP-teljes probléma polinomidejű megoldása az összes többi polinomidejű megoldásához vezetne. Hogy van-e ilyen polinomidejű algoritmus, az a Clay Matematikai Intézet listáján szereplő ,,P versus NP'' probléma (ahol tehát P a polinomidőben megoldható, NP a polinomidőben ellenőrizhető problémák halmaza). Ennek megoldásáért egymillió dolláros jutalom járna. A probléma mai állásáról Aaronson írt nemrég áttekintő cikket [5].

A gráf-izomorfizmus probléma egyike a nagyon kisszámú ismert természetes problémának, amelyről nem ismeretes, hogy NP-teljes lenne, de amelynek megoldására nem ismert polinomidejű algoritmus sem. Egy másik ilyen nevezetes probléma a prímfaktorizáció, azaz egy természetes szám prímszámokra való gyors felbontásának kérdése. A probléma NP-beli, egy megadott felbontásról gyorsan el lehet dönteni, hogy jó-e valójában. A jelenleg ismert leggyorsabb algoritmus erre a problémára ugyanúgy mérsékelten exponenciális ( $\exp(n^{1/3})$ körüli) mint a korábbi legjobb algoritmus az IZO probléma megoldására.

Matematikailag a két problémának kevés köze van egymáshoz. De Babai áttörése egy pszichológiai korlátot is áttört és várható hogy most sokan nekiveselkednek a prímfaktorizációs probléma megoldásának. Ha erre valaki igazán gyors algoritmust talál, az a kódoláselmélet számára elég nagy csapás lesz. A ma általánosan használt gyakorlati kriptográfia arra épül, hogy a prímfaktorizációt nem tudjuk megoldani a gyakorlatban, még nagy teljesitményű számítógépekkel sem. Egy elméleti áttörés ebben a témában alapvetően változtathatja meg, hogy például a különféle titkosszolgálatok illetve a bankok mit tartanak biztonságos kódolási módszernek.

Babai eredménye a gráf-izomorfizmus problémát az exponenciálishoz közeli bonyolultságú problémák közül a majdnem polinomiális bonyolultságú problémák közé helyezi. Korábban Eugene Luks talált polinomidejű IZO algoritmust a korlátos fokú gráfokra. Azaz egy olyan algoritmust, amelynek futási ideje $n^{c(D)}$ , ahol $D$ egy felső korlát a vizsgált gráfok maximális fokára. Algoritmusa lényeges módon épít véges csoportelméleti eredményekre. A korábbi legjobb általános algoritmus, amelyet Luks talált 1983-ban, mérsékelten exponenciális futási idejű volt. Valójában Babai egy, a gráf-izomorfizmus problémánál általánosabb, az algoritmikus csoportelmélethez tartozó problémát old meg. Ez a színezett halmazok $G$ -izomorfia problémája:

Legyen $G$ egy, az $R$ halmazon ható permutációcsoport ( $G$ -t a generáló permutációk egy halmaza segítségével adjuk meg). Ha adott az $R$ halmaz két színezése, akkor az a kérdés, hogy a két színezés egymásba $G$ -beli elemmel átvihető-e.

Könnyen látható, hogy az IZO ennek a problémának speciális esete. Tekintsük ugyanis a $\operatorname{Sym}(n)$ csoport hatását a rendezetlen párok $R$ halmazán. Ez egy $\binom{n}{2}$ fokú $G$ permutációcsoport. Egy $n$ pontú $X$ gráfnak természetes módon megfelel az $R$ halmaz egy 2 színnel való színezése. Az IZO megoldásához elég a fenti $G$ csoportra megoldani a színezett halmazok $G$ -izomorfia problémáját.

Babai eredeti bizonyítása használja a Véges Egyszerű Csoportok Osztályozását (amelynek bizonyítását 10000 oldalra becsülik). Pontosabban, felhasználja az úgynevezett Schreier-sejtést, mely szerint a véges egyszerű csoportok külső automorfizmuscsoportja feloldható. Ez a klasszifikációs tétel egy elegáns egymondatos következménye.

Jelen cikk szerzőjének sikerült ezt a mondatot egy másik, pár oldalon elemien bizonyítható mondatra kicserélni [6], amelynek felhasználásával Babai algoritmusának egy gyengébb, de még mindig kvázipolinomiális változata adható meg.

Természetes kérdés, hogy van-e polinomiális algoritmus az IZO problémára. A Babai által használt módszerek, mint például a felhasznált csoportelméleti állítások azt jelzik, hogy egy ilyen algoritmus megalkotásához alapvető új ötletekre van szükség. Az azonban most már nagyon valószínűtlen, hogy a gráf-izomorfizmus probléma NP-teljes legyen. Ahogy Babai cikkében [2] megjegyzi, ez esetben minden NP-beli probléma megoldására létezne kvázipolinomiális algoritmus.

Pyber László

Irodalomjegyzék

1: B. D. McKay, A. Piperno: Practical Graph Isomorphism, II, arXiv:1301.1493, 2013.
2: L. Babai: Graph Isomorphism in quasipolynomial time. arXiv:1512.03547, 2015.
3: H. A. Helfgott: Isomorphismes de graphes en temps quasi-polynomial. arXiv:1701.04372, 2017.
4: S. A. Cook: The complexity of theorem proving procedures, Proc 3rd ACM STOC (1971), 151—158.
5: S. Aaronson: P 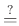$\mathop{=}\limits^?$ NP, kézirat Scott Aaronson ,,Shtetl-Optimized'' cimű blogján.
6: L. Pyber: A CFSG-free analysis of Babai's quasipolynomial GI algorithm. arXiv:1605.08266, 2016.
7: E. M. Luks: Isomorphism of graphs of bounded valence can be tested in polynomial time. J. Comput. Syst. Sci. 25 (1982), 42—65.