Ha két fenti ![]() környezet metszete nemüres, akkor a
környezet metszete nemüres, akkor a ![]() átmenő-függvény (mely most
átmenő-függvény (mely most ![]() két nyílt része közötti leképezés lesz) mutatja meg, hogy a két térképet hogyan kell a sokaságban "összepasszítani". Ahhoz azonban, hogy az analízis jól ismert fogalmait és módszereit (pl. a differenciálhatóságot) használni tudjuk, további feltételekre van szükségünk. Egy
két nyílt része közötti leképezés lesz) mutatja meg, hogy a két térképet hogyan kell a sokaságban "összepasszítani". Ahhoz azonban, hogy az analízis jól ismert fogalmait és módszereit (pl. a differenciálhatóságot) használni tudjuk, további feltételekre van szükségünk. Egy ![]() függvény az
függvény az ![]() pontban differenciálható, ha egy
pontban differenciálható, ha egy ![]() térképre az
térképre az ![]() kompozíció (mint
kompozíció (mint ![]() függvény) a
függvény) a ![]() pontban differenciálható. Sajnos ez a tulajdonság függhet az
pontban differenciálható. Sajnos ez a tulajdonság függhet az ![]() -et tartalmazó térkép választásától. Ennek elkerülésére azt mondjuk, hogy az
-et tartalmazó térkép választásától. Ennek elkerülésére azt mondjuk, hogy az ![]() térkép-halmaz egy differenciálható atlasz, ha
térkép-halmaz egy differenciálható atlasz, ha ![]() (vagyis a térképek lefedik
(vagyis a térképek lefedik ![]() -et), és a halmazhoz tartozó térképek párjaira az átmenő-függvények (mint
-et), és a halmazhoz tartozó térképek párjaira az átmenő-függvények (mint ![]() nyílt részei közötti leképezések) differenciálhatóak. Ekkor az
nyílt részei közötti leképezések) differenciálhatóak. Ekkor az ![]() halmazból vett térképeket használva függvények pontonkénti differenciálhatósága már probléma nélkül definiálható, és valójában az analízis sok eredménye átemelhető ebbe a topologikus kontextusba. Ugyanígy egy
halmazból vett térképeket használva függvények pontonkénti differenciálhatósága már probléma nélkül definiálható, és valójában az analízis sok eredménye átemelhető ebbe a topologikus kontextusba. Ugyanígy egy ![]() leképezés differenciálhatósága is egyszerűen definiálható, amennyiben a sokaságokon
leképezés differenciálhatósága is egyszerűen definiálható, amennyiben a sokaságokon ![]() és
és ![]() differenciálható atlaszokat rögítünk. (Ezen atlaszok választását ezentúl beleértjük az
differenciálható atlaszokat rögítünk. (Ezen atlaszok választását ezentúl beleértjük az ![]() differenciálható sokaság definíciójába.) Egy
differenciálható sokaság definíciójába.) Egy ![]() leképezést diffeomorfizmusnak hívunk, ha homeomorfizmus, és mind
leképezést diffeomorfizmusnak hívunk, ha homeomorfizmus, és mind ![]() , mind
, mind ![]() differenciálhatóak.
differenciálhatóak.
Természetes kérdés az, hogy mely sokaságokra létezik differenciálható atlasz, és mikor egyértelmű ez. Ismert például, hogy legfeljebb 3 dimenziós sokaságokra mindig létezik differenciálható atlasz, és az diffeomorfizmus erejéig egyértelmű — ez a tétel fontos lépés például Perelmannak a Poincaré-sejtésre adott megoldásában. Magasabb dimenzióban ez az elv általában nem teljesül: vannak olyan sokaságok (már 4-dimenzióban is) melyeken nem létezik differenciálható atlasz, és rengeteg olyan van, amin több (sőt 4-dimenzióban végetelen sok) különböző is létezik. A továbbiakban csak euklideszi terekre (vagyis ![]() -ekre) szorítkozunk. Ezeken a tereken természetesen mindig van egy differenciálható atlasz: maga az egész tér (az identitás-függvénnyel). Az egyértelműség tekintetében a következő klasszikus eredmény ismert:
-ekre) szorítkozunk. Ezeken a tereken természetesen mindig van egy differenciálható atlasz: maga az egész tér (az identitás-függvénnyel). Az egyértelműség tekintetében a következő klasszikus eredmény ismert:
Tétel: Ha az ![]() differenciálható sokaság
differenciálható sokaság ![]() -nel homeomorf, és
-nel homeomorf, és ![]() teljesül, akkor
teljesül, akkor ![]() és
és ![]() diffeomorfak. Vagyis minden olyan
diffeomorfak. Vagyis minden olyan ![]() -en, amire
-en, amire ![]() teljesül, (diffeomorfizmus erejéig) egyetlen differenciálható struktúra létezik.
teljesül, (diffeomorfizmus erejéig) egyetlen differenciálható struktúra létezik.
A 4-dimenziós eset azonban ettől jelentősen különbözik. Egy olyan differenciálható sokaságot, amely ![]() -gyel homeomorf, de nem diffeomorf, egzotikus
-gyel homeomorf, de nem diffeomorf, egzotikus ![]() -nek hívjuk.
-nek hívjuk.
Tétel: Minden ![]() valós számhoz létezik egy olyan
valós számhoz létezik egy olyan ![]() sokaság, mely homeomorf
sokaság, mely homeomorf ![]() -gyel, de
-gyel, de ![]() és
és ![]() csak akkor diffeomorfak, ha
csak akkor diffeomorfak, ha ![]() . Másképpen szólva, kontinuum sok kölönböző egzotikus
. Másképpen szólva, kontinuum sok kölönböző egzotikus ![]() létezik.
létezik.
Nem könnyű egy ilyen sokaságot elkészíteni, vagy éppenséggel elképzelni. A továbbiakban egy konstrukciót adunk egy egzotikus ![]() -re. Ennek során egy bizonyos tulajdonságú, a 3-dimenziós terünkben lévő csomó létezését fogjuk feltételezni. Ez utóbbi létezésének bizonyítása messze nem egyszerű feladat; így az alább ismertetendő módszer nem igazán egyszerűbbé, inkább szemléletesebbé, "hihetőbbé'' teszi egzotikus euklideszi terek létezését. A végső lépésben az egzotikusság bizonyításához (természetesen) a 4-dimenziós topológia csúcseredményeire lesz szükségünk.
-re. Ennek során egy bizonyos tulajdonságú, a 3-dimenziós terünkben lévő csomó létezését fogjuk feltételezni. Ez utóbbi létezésének bizonyítása messze nem egyszerű feladat; így az alább ismertetendő módszer nem igazán egyszerűbbé, inkább szemléletesebbé, "hihetőbbé'' teszi egzotikus euklideszi terek létezését. A végső lépésben az egzotikusság bizonyításához (természetesen) a 4-dimenziós topológia csúcseredményeire lesz szükségünk.
Legyen tehát ![]() egy csomó
egy csomó ![]() -ban (vagy, ekvivalens módon a 3-dimenziós
-ban (vagy, ekvivalens módon a 3-dimenziós ![]() gömbfelületben): vagyis vegyük az
gömbfelületben): vagyis vegyük az ![]() körvonalnak
körvonalnak ![]() -ba egy differenciálható beágyazását. Az
-ba egy differenciálható beágyazását. Az ![]() gömbfelületet a
gömbfelületet a ![]() 4-dimenziós golyó peremeként tekintve a
4-dimenziós golyó peremeként tekintve a ![]() csomónak két tulajdonságát definiálhatjuk:
csomónak két tulajdonságát definiálhatjuk: ![]() topologikus metszet ha a
topologikus metszet ha a ![]() szorzattérnek van olyan folytonos beágyazása
szorzattérnek van olyan folytonos beágyazása ![]() -be, hogy
-be, hogy ![]() a
a ![]() golyó
golyó ![]() peremébe képződik, és a
peremébe képződik, és a ![]() középkör épp
középkör épp ![]() -t adja. A csomó sima metszet, ha a
-t adja. A csomó sima metszet, ha a ![]() -nek létezik fenti tulajdonságú differenciálható beágyazása. (Ez a két tulajdonság fogja tehát a csomók szintjén a folytonos és differenciálható közötti különbséget mérni — éppen azt a tulajdonságot, amitől egy tér egzotikus lesz majd.)
-nek létezik fenti tulajdonságú differenciálható beágyazása. (Ez a két tulajdonság fogja tehát a csomók szintjén a folytonos és differenciálható közötti különbséget mérni — éppen azt a tulajdonságot, amitől egy tér egzotikus lesz majd.)
Egy olyan ![]() csomó, mely topologikus metszet, de nem sima metszet, egy egzotikus
csomó, mely topologikus metszet, de nem sima metszet, egy egzotikus ![]() -et ad a következő módon. Képzeljük el a 4-dimenziós
-et ad a következő módon. Képzeljük el a 4-dimenziós ![]() gömbfelületet mint két 4-dimenziós
gömbfelületet mint két 4-dimenziós ![]() golyó (
golyó (![]() és
és ![]() ) uniója, melyek az
) uniója, melyek az ![]() peremük mentén vannak összeragasztva. Ebben az
peremük mentén vannak összeragasztva. Ebben az ![]() -ban van a fenti tulajdonságú
-ban van a fenti tulajdonságú ![]() csomónk. Emlékezzünk még, hogy ha
csomónk. Emlékezzünk még, hogy ha ![]() -ből elhagyunk egy pontot, akkor épp az
-ből elhagyunk egy pontot, akkor épp az ![]() Euklideszi teret kapjuk.
Euklideszi teret kapjuk.
Legyen a folytonosan beágyazott ![]() (melyre
(melyre ![]() épp
épp ![]() -t adja) képe
-t adja) képe ![]() . (Ennek létezése következik abból, hogy választott csomónk topologikus metszet.) Ilymódon az
. (Ennek létezése következik abból, hogy választott csomónk topologikus metszet.) Ilymódon az ![]() gömbfelület felbontható a
gömbfelület felbontható a ![]() és a
és a ![]() részeinek uniójára, melyek egy 3-sokaság mentén vannak összeragasztva. (Ezt a 3-sokaságot a
részeinek uniójára, melyek egy 3-sokaság mentén vannak összeragasztva. (Ezt a 3-sokaságot a ![]() menti 0-műtét adja meg, de ez a mostani konstrukció szempontjából lényegtelen.) Szemléletesen szólva, az
menti 0-műtét adja meg, de ez a mostani konstrukció szempontjából lényegtelen.) Szemléletesen szólva, az ![]() felbontást úgy változtatjuk meg, hogy
felbontást úgy változtatjuk meg, hogy ![]() -t áttesszük
-t áttesszük ![]() -ből
-ből ![]() -be.
-be.
A ![]() peremes 4-sokaság valójában úgy keletkezik, hogy a 4-dimenziós golyóhoz egy ún. 4-dimenziós 2-fogantyút ragasztunk, így ennek a résznek természetesen adódik egy differenciálható struktúrája. Vegyük most a
peremes 4-sokaság valójában úgy keletkezik, hogy a 4-dimenziós golyóhoz egy ún. 4-dimenziós 2-fogantyút ragasztunk, így ennek a résznek természetesen adódik egy differenciálható struktúrája. Vegyük most a ![]() részt (ami szintén egy kompakt 4-dimenziós peremes sokaság), és hagyjunk el belőle egy pontot. A kapott peremes, nem-kompkat 4-sokaság Freedman és Quinn egy nevezetes és mély tétele miatt ellátható egy differenciálható struktúrával. (Ebben a tételben a nem-kompaktság nagyon fontos — szemléletesen az történik, hogy a problémás pontokat el tudjuk küldeni a "végtelenbe'', ami nem-kompakt esetben egy lehetőség, a kompakt esetben azonban nem. Ennek a heurisztikus gondolatnak szigorú matematikai tétellé formálása meghökkentően nehéz apparátust igényel.) Mivel egy 3-dimenziós sokaságon a differenciálható struktúra egyértelmű, a kapott két differenciálható sokaság (
részt (ami szintén egy kompakt 4-dimenziós peremes sokaság), és hagyjunk el belőle egy pontot. A kapott peremes, nem-kompkat 4-sokaság Freedman és Quinn egy nevezetes és mély tétele miatt ellátható egy differenciálható struktúrával. (Ebben a tételben a nem-kompaktság nagyon fontos — szemléletesen az történik, hogy a problémás pontokat el tudjuk küldeni a "végtelenbe'', ami nem-kompakt esetben egy lehetőség, a kompakt esetben azonban nem. Ennek a heurisztikus gondolatnak szigorú matematikai tétellé formálása meghökkentően nehéz apparátust igényel.) Mivel egy 3-dimenziós sokaságon a differenciálható struktúra egyértelmű, a kapott két differenciálható sokaság (![]() és
és ![]() ) egy differenciálható sokasággá — nevezzük
) egy differenciálható sokasággá — nevezzük ![]() -nak — ragad össze.
-nak — ragad össze.
Mivel topologikusan pusztán egy pontot hagytunk el ![]() -ből, az összeragasztott sokaság homeomorf lesz
-ből, az összeragasztott sokaság homeomorf lesz ![]() -gyel. Azonban abból a tulajdonságból, hogy
-gyel. Azonban abból a tulajdonságból, hogy ![]() nem sima metszet, az következik, hogy
nem sima metszet, az következik, hogy ![]() nem diffeomorf
nem diffeomorf ![]() -gyel. Valóban, ha
-gyel. Valóban, ha ![]() és
és ![]() diffeomorfak, akkor
diffeomorfak, akkor ![]() -hoz egy pontot adhatunk úgy, hogy
-hoz egy pontot adhatunk úgy, hogy ![]() -et kapjuk, és ekkor az
-et kapjuk, és ekkor az ![]() rész képe egy sima metszet körlap lenne
rész képe egy sima metszet körlap lenne ![]() számára, ami ellentmond a feltett tulajdonságnak.
számára, ami ellentmond a feltett tulajdonságnak.
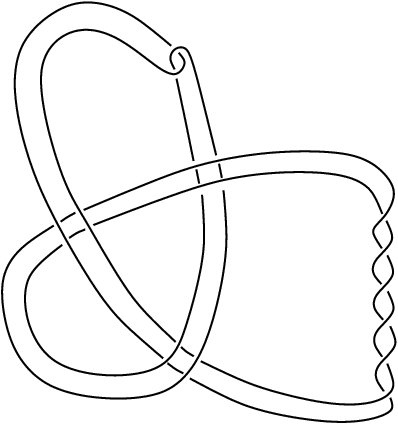
Egy egzotikus ![]() létezésének belátásához azonban szükségünk van egy megfelelő
létezésének belátásához azonban szükségünk van egy megfelelő ![]() csomóra: egy olyanra, ami simán nem metszet, de topologikusan az. Az alábbi rajzon bemutatott csomóra egyszerűen kiszámolható, hogy Alexander polinomja azonosan 1. (Mind egy csomó Alexander polinomja, mind az előbb említett számolás meglehetősen elemi módszereket igénylő egyszerű feladat.) Ebből Freedman egy (Fields medállal díjazott) mély eredménye szerint következik, hogy a csomó topologikus metszet. Ezzel szemben Donaldson (szintén Fields medállal díjazott) módszerét alkalmazva belátható, hogy a csomó nem sima metszet. (Ez utóbbi eredmény most már aránylag elemi eszközökkel is bebizonyítható — egy ilyen bizonyítás található meg Ozsváth, Szabó és a szerző Grid homology for knots and links című könyvében.)
csomóra: egy olyanra, ami simán nem metszet, de topologikusan az. Az alábbi rajzon bemutatott csomóra egyszerűen kiszámolható, hogy Alexander polinomja azonosan 1. (Mind egy csomó Alexander polinomja, mind az előbb említett számolás meglehetősen elemi módszereket igénylő egyszerű feladat.) Ebből Freedman egy (Fields medállal díjazott) mély eredménye szerint következik, hogy a csomó topologikus metszet. Ezzel szemben Donaldson (szintén Fields medállal díjazott) módszerét alkalmazva belátható, hogy a csomó nem sima metszet. (Ez utóbbi eredmény most már aránylag elemi eszközökkel is bebizonyítható — egy ilyen bizonyítás található meg Ozsváth, Szabó és a szerző Grid homology for knots and links című könyvében.)
Tehát a fenti módszert a rajzon látható csomóra alkalmazva egy egzotikus ![]() adódik. Arra azonban fel szeretnénk hívni a figyelmet, hogy ennek az objektumnak (a létezésén kívül) nem sok tulajdonságát ismerjük. A fenti módszerben két olyan lépés is volt (az egyik Freedman tételén alapult, és
adódik. Arra azonban fel szeretnénk hívni a figyelmet, hogy ennek az objektumnak (a létezésén kívül) nem sok tulajdonságát ismerjük. A fenti módszerben két olyan lépés is volt (az egyik Freedman tételén alapult, és ![]() létezését garantálta, a másik Freedman és Quinn tétele volt, mely a nem-kompakt 4-sokaságon lévő differenciálható struktúrát adta), melyek messze nem konstruktívak.
létezését garantálta, a másik Freedman és Quinn tétele volt, mely a nem-kompakt 4-sokaságon lévő differenciálható struktúrát adta), melyek messze nem konstruktívak.