Nevezetes egyenlőtlenségek a középiskolában
A kétszintű érettségi bevezetésével a korábbi évekhez képest nagyobb hangsúlyt kapott a nevezetes közepek témaköre. Az emelt szintű érettségin, valamint a hazai és nemzetközi matematikaversenyeken gyakran szerepelnek olyan bizonyítandó egyenlőtlenségek, szélsőérték-problémák, amelyek megoldásában fontos szerepet játszanak a nevezetes egyenlőtlenségek. Emiatt annak, aki sikeresen szeretne szerepelni ezeken a megmérettetéseken, elengedhetetlenül szükséges, hogy minél nagyobb jártasságra tegyen szert ebben a témakörben. Ezért fontos, hogy az emelt szintű matematikaórák és a tehetséggondozó foglalkozások tananyagában szerepeljen ez a témakör.
Mivel a Szegedi Radnóti Miklós Kísérleti Gimnázium speciális matematika, illetve matematika-fizika tagozatán, valamint az Erdős Pál Matematikai Tehetséggondozó Iskolában (EPMTI) is tanítok, ezért jelen cikkben szeretném felvázolni azt az utat, ahogy ezen tehetséggondozó műhelyekben eljutunk a legegyszerűbb egyenlőtlenségektől az olimpiai szintű feladatokig. Feltett szándékom, hogy ezzel az összeállítással segítséget nyújtsak azon kollégáknak is, akik tehetséggondozó szakkörökön szeretnének foglalkozni a nevezetes egyenlőtlenségek témakörével. Úgy gondolom, hogy egy ilyen cikk akkor hasznos igazán, ha a benne leírtakat sikerrel tudják alkalmazni a kollégák a mindennapi munkájukban.
A cikk alapjául a 63. Rátz László Vándorgyűlésen elhangzott előadásom anyaga szolgált.
Fontosabb egyenlőtlenségek és kapcsolatrendszerük
A matematikai tehetséggondozásban eltöltött bő harminc évem alatt azt tapasztaltam, hogy a tehetséges diákok számára a leghatékonyabb tanítási módszer a felfedeztető matematikaoktatás. Ezt igyekszem alkalmazni speciális matematika tagozaton, az EPMTI-ben és szakkörökön is.
Úgy gondolom, ennek lényeges része, hogy az egyes témakörökhöz tartozó feladatsorok fokozatosan nehezedő és egymásra épülő problémákat tartalmazzanak. Ezzel segíthetjük a fiatalokat a felfedező munkájukban. Emellett fontosnak tartom, hogy együtt gondolkodjunk a tanulókkal, és elakadásuk esetén kérdéseinkkel segítsük, vezessük a tananyag feldolgozását. Közben ők is szembesülnek azzal, hogy a megfelelően megfogalmazott kérdések milyen mértékben tudják segíteni a problémamegoldást.
A fokozatosság elvét tartottam szem előtt az Egyenlőtlenség I. és II. című könyvem felépítésénél, és azt veszem figyelembe a témakör tanítása során is.

Ezért az ismerkedés az egyenlőtlenségek témakörével egy egyszerű állítással indul: bármely valós szám négyzete nemnegatív. Erre építve kerül elő a Cauchy−Bunyakovszkij−Schwarz-egyenlőtlenség (CBS), a hatványközepek elmélete, majd a Bernoulli-, Hölder-, Minkowski- és Muirhead-egyenlőtlenség. Emellett megjelenik a rendezési tétel (Szűcs Adolf-tétel) és a felhasználásával levezethető Csebisev-egyenlőtlenség. Mindezt megkoronázhatjuk a gyengén konvex, illetve konkáv függvények elméletével és a Jensen-egyenlőtlenséggel, ami szoros kapcsolatban van a korábban már említett egyenlőtlenségek egy részével. Ez viszont már egy külön cikk témája lehet.
Az említett egyenlőtlenségek közötti kapcsolatrendszert az alábbi ábra mutatja:

Teljes négyzetek összege, kéttagú közepek
Speciális matematika tagozaton a 7. és 8., míg a négy évfolyamos matematika tagozaton, tehetséggondozó szakkörökön és az EPMTI-ben 9. osztályban nagyon fontos a szilárd matematikai alapok megteremtése. Ha ebben az időszakban természetessé válnak az alapvető algebrai átalakítások, és kialakul az igény a precíz, pontos matematikai bizonyításra, akkor a későbbiekben arra is lehetőség nyílik, hogy elmerülhessünk komolyabb, fajsúlyosabb témákban is.
Mind a bizonyítási, mind az algebrai készségek kifejlesztésében nagyon hatékony segítséget nyújtanak a teljes négyzetek kialakítására vezető egyenlőtlenségek és a velük ekvivalens, kéttagú hatványközepek alkalmazását igénylő problémák. Ezért a kezdeti időszakban a nevezetes egyenlőtlenségek témakörét a „bármely valós szám négyzete nemnegatív” gondolattal vezethetjük be. Az ehhez kapcsolódó feladatokkal színesíthetjük a nevezetes szorzatok begyakorlására szánt órákat és lehetőség nyílik arra, hogy a diákok megismerjék a matematikai bizonyítás metódusát.
Többek között a következő összeállításban szereplő, fokozatosan nehezedő feladatokat szoktam feladni ezeken az órákon. A feladatok mellett zárójelben szerepel, hogy melyik szakirodalomban, hol található meg a feladat megoldása. (További feladatok találhatók az [1] II. fejezetében és a [2] 1. fejezetének elején.)
Bármely valós szám négyzete nemnegatív
1. Igazoljuk az
a) 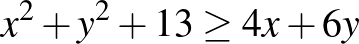 ; ([1] 18. oldal)
; ([1] 18. oldal)
b) 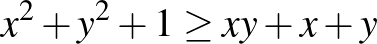 ; ([1] 18. oldal)
; ([1] 18. oldal)
c) 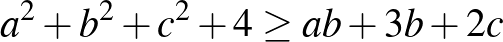 ([1] 167. oldal)
([1] 167. oldal)
egyenlőtlenségeket! Mikor áll fenn egyenlőség?
2. Oldjuk meg az alábbi egyenleteket:
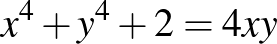 ; ([1] 168. oldal)
; ([1] 168. oldal)
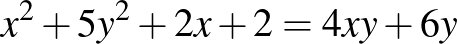 . ([1] 168. oldal)
. ([1] 168. oldal)
3. Bizonyítsuk be, hogy bármely  ,
,  ,
,  valós szám esetén fennáll az
valós szám esetén fennáll az  egyenlőtlenség! ([1] 20. oldal)
egyenlőtlenség! ([1] 20. oldal)
4. Bizonyítsuk be, hogy bármely  ,
,  ,
,  valós szám esetén fennáll az
valós szám esetén fennáll az 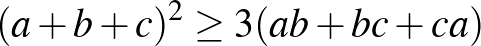 egyenlőtlenség!
egyenlőtlenség!
5. Mutassuk meg, hogy ha az  ,
,  ,
,  valós számokra
valós számokra 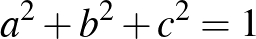 , akkor teljesül a következő egyenlőtlenség:
, akkor teljesül a következő egyenlőtlenség:  .
.
6. Jelölje  ,
,  és
és  egy háromszög oldalait. Állapítsuk meg, hogy milyen határok közé eshet a következő hányados értéke:
egy háromszög oldalait. Állapítsuk meg, hogy milyen határok közé eshet a következő hányados értéke: 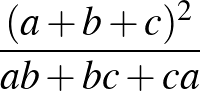 . (Nemzetközi Magyar Matematikaverseny (NMMV). Könnyebb formában, a határok megadásával, Arany Dániel Matematikai Tanulóverseny (ADV) haladók, II. kat. 2. ford. 2017.)
. (Nemzetközi Magyar Matematikaverseny (NMMV). Könnyebb formában, a határok megadásával, Arany Dániel Matematikai Tanulóverseny (ADV) haladók, II. kat. 2. ford. 2017.)
7. Bizonyítsa be, hogy ha  ,
,  pozitív valós számok és
pozitív valós számok és  tetszőleges valós szám, akkor
tetszőleges valós szám, akkor 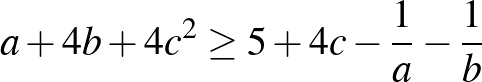 . (ADV kezdők, döntő 1995.)
. (ADV kezdők, döntő 1995.)
A fenti feladatok közül kiemelném a harmadikat. Ez több szempontból is fontos egyenlőtlenség. Egyrészt azért, mert az ekvivalens átalakítások során a teljes négyzetek összegének kialakításához szükség van arra, hogy az egyenlőtlenség mindkét oldalát megszorozzuk 2-vel. Erre, illetve ehhez hasonló „trükkre” szükség van az 1. b), illetve d) feladatban is. Másrészt azért, mert a későbbiekben az összetettebb feladatok között találkozhatunk számos olyannal, amely erre az egyszerű egyenlőtlenségre vezet.
Az előző, alapozó feladatsor után már eredményesebben térhetünk át a kéttagú közepekre, amelyek alkalmasak arra, hogy bevezessék a hatványközepek témakörét. A kéttagú közepekhez kapcsolódó feladatok egy része visszavezethető teljes négyzetek összegére. Ettől függetlenül kiválóan alkalmasak arra, hogy rajtuk keresztül bevezessük és szemléltessük azt, ahogy a nevezetes egyenlőtlenségeket alkalmazzuk bizonyítások és szélsőérték-feladatok megoldásában. Az ilyen jellegű problémákra láthatunk példákat az alábbi feladatsorban.
Kéttagú közepek
Ha 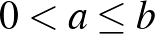 , akkor
, akkor  .
.
1. Bizonyítsuk be, hogy bármely pozitív valós szám és reciprokának összege legalább 2.
2. Bizonyítsuk be, hogy bármely negatív valós szám és reciprokának összege legfeljebb 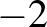 .
.
3. Legyen  ,
,  és
és  pozitív valós szám. Bizonyítsuk be, hogy ekkor
pozitív valós szám. Bizonyítsuk be, hogy ekkor
a) 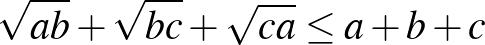 ; ([2] 54. oldal)
; ([2] 54. oldal)
b) 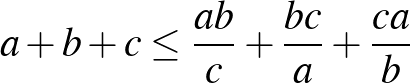 ; ([2] 52. oldal)
; ([2] 52. oldal)
c) 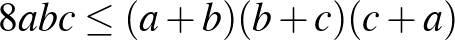 ; ([1] 183. oldal)
; ([1] 183. oldal)
d) 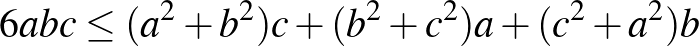 ; ([1] 183. oldal)
; ([1] 183. oldal)
e) 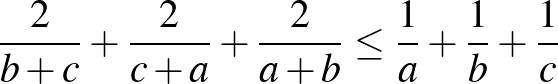 . ([1] 66. oldal)
. ([1] 66. oldal)
4. Legyen  ,
,  és
és  pozitív egész szám. Határozzuk meg az
pozitív egész szám. Határozzuk meg az
![$\displaystyle \frac{[a,b]+(b,c)}{b}+\frac{[b,c]+(c,a)}{c}+\frac{[c,a]+(a,b)}{a}
$](/images/stories/latexuj/2025-01/2025-01-nevezetesegyenlotlensegek/img23.png)
összeg minimumát, ha ![$[x,y]$](/images/stories/latexuj/2025-01/2025-01-nevezetesegyenlotlensegek/img24.png) az
az 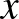 és
és 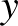 pozitív egész szám legkisebb közös többszöröse, míg az
pozitív egész szám legkisebb közös többszöröse, míg az 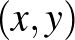 a legnagyobb közös osztója!
a legnagyobb közös osztója!
5. Bizonyítsuk be, hogy bármely  ,
,  ,
,  pozitív valós számra fennáll az
pozitív valós számra fennáll az 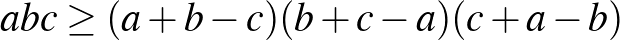 . (Schur-egyenlőtlenség speciális esete)
. (Schur-egyenlőtlenség speciális esete)
6. Bizonyítsuk be, hogy ha  ,
,  ,
,  pozitív valós számok, akkor
pozitív valós számok, akkor 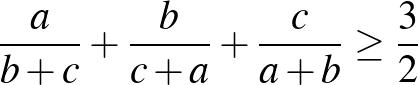 . (Nesbitt-egyenlőtlenség)
. (Nesbitt-egyenlőtlenség)
Az 5. feladat (Schur-egyenlőtlenség speciális esete) több okból kifolyólag is nagy jelentőséggel bír.
Egyrészt egy lehetséges megoldása az úgynevezett dualitási elv felhasználásával történhet, amit hatékonyan alkalmazhatunk sok egyenlőtlenség bizonyításánál.
Az elv lényege, hogy az  ,
,  ,
,  pozitív valós számok akkor és csak akkor képezik egy háromszög oldalainak a hosszát, ha léteznek olyan
pozitív valós számok akkor és csak akkor képezik egy háromszög oldalainak a hosszát, ha léteznek olyan 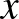 ,
, 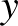 ,
, 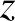 pozitív valós számok, amelyekre
pozitív valós számok, amelyekre 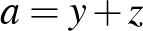 ,
, 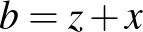 ,
,  .
.
Hogyan használhatjuk ezt a gondolatot a feladat megoldásában?
Azt könnyű meggondolni, hogy a jobb oldalon álló tényezők közül legfeljebb csak egy lehet nempozitív. Ha ez teljesül, akkor a jobb oldal nempozitív, míg a bal oldal pozitív, így fennáll az egyenlőtlenség. A továbbiakban legyen mindhárom tényező pozitív, azaz  ,
,  és
és  egy háromszög oldalai.
egy háromszög oldalai.
Ekkor legyen 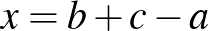 ,
, 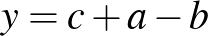 ,
, 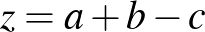 , tehát
, tehát
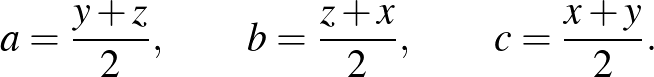
Így a bizonyítandó egyenlőtlenség az 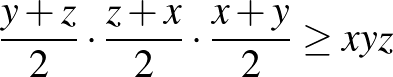 alakú lesz.
alakú lesz.
Alkalmazzuk a bal oldali kifejésekre a kéttagú számtani és mértani közép közötti egyenlőtlenséget:
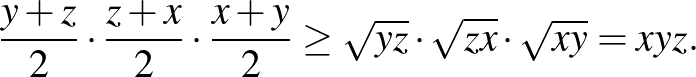
Egyenlőség akkor és csak akkor áll fenn, ha 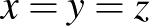 , ami pedig pontosan akkor áll fenn, ha
, ami pedig pontosan akkor áll fenn, ha 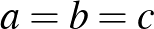 .
.
Másrészt a nehezebb problémák között kimondottan sok olyan található, amely erre az egyenlőtlenségre vagy ennek valamelyik formájára vezet:

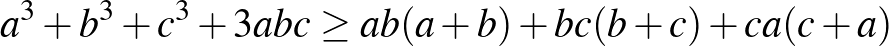 ;
;

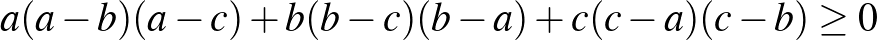 .
.
Az előző összeállításból még a 6. feladatot, a Nesbitt-egyenlőtlenséget emelném ki. Mivel számos bizonyítása létezik, ezért kiválóan alkalmas arra, hogy rajta keresztül bemutassunk néhány módszert. Emellett ez az egyenlőtlenség is megjelenik sok feladatban.
Most felvázolom két olyan bizonyítását, ami az eddigiek szép alkalmazása.
Az első a diákok részéről teljesen természetes „ledúrjuk” módszer alkalmazása. Szorozzuk be mindkét oldalt a pozitív 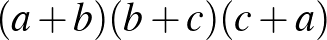 szorzattal, majd rendezzük az egyenlőtlenséget. Ekkor az eredetivel ekvivalens
szorzattal, majd rendezzük az egyenlőtlenséget. Ekkor az eredetivel ekvivalens
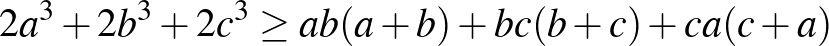
alakhoz jutunk. Nullára redukálás és megfelelő párosítás után az eredetivel ekvivalens, teljes négyzetek összegére vezető egyenlőtlenséget kapjuk:
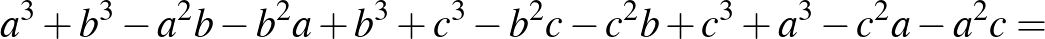 |
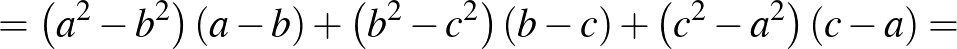 |
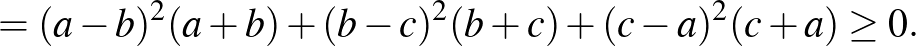 |
Egyenlőség akkor és csak akkor áll fenn, ha 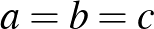 .
.
A másik megoldásnál a korábban említett dualitási elvet alkalmazhatjuk úgy, hogy legyen 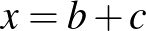 ,
, 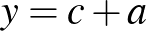 ,
,  . Ekkor
. Ekkor 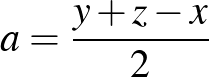 ,
, 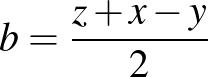 ,
,  . Ezek felhasználásával az eredetivel ekvivalens
. Ezek felhasználásával az eredetivel ekvivalens

egyenlőtlenséget kapjuk. Erről pedig egyszerű átrendezéssel látható, hogy ekvivalens az
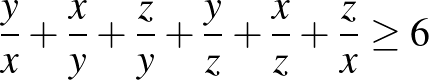
nyilvánvaló egyenlőtlenséggel, hiszen ennek a bal oldalán háromszor szerepel egy pozitív szám és reciprokának az összege.
Cauchy–Bunyakovszkij–Schwarz-egyenlőtlenség (CBS)
A teljes négyzetek összegének gondolatköréhez sorolható a Cauchy–Bunyakovszkij–Schwarz-egyenlőtlenség (CBS), vagy röviden Cauchy-egyenlőtlenség is. Ugyanis tekintsük a valós számok halmazán értelmezett
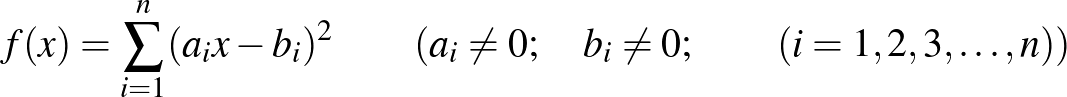
hozzárendelési szabályú függvényt. Nyilván ez a függvény bármely valós 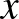 esetén nemnegatív értéket vesz fel, ami azt jelenti, hogy a hozzá tartozó diszkrimináns nempozitív értékű. Ezt felírva és átrendezve kapjuk a
esetén nemnegatív értéket vesz fel, ami azt jelenti, hogy a hozzá tartozó diszkrimináns nempozitív értékű. Ezt felírva és átrendezve kapjuk a
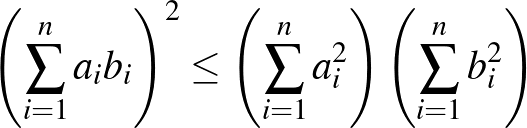
CBS-t. Itt egyenlőség akkor és csak akkor áll fenn, ha az f függvény 0-t vesz fel, ami pontosan akkor lehetséges, ha  .
.
A CBS-ből könnyen kapjuk az úgynevezett Titu-lemmát (lásd [1] 37. oldal), amely az
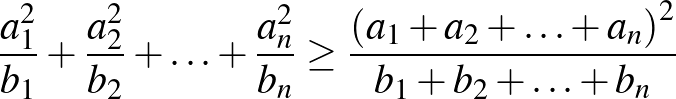
egyenlőtlenség, ahol  és
és 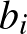 pozitív valós számok (
pozitív valós számok (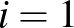 , 2, 3, ...,
, 2, 3, ...,  ).
).
Néhány gondolat erejéig térjünk vissza a Nesbitt-egyenlőtlenséghez, mert annak egy újabb bizonyításában a Titu-lemma olyan alkalmazását mutathatjuk meg, ami sok feladat megoldásában visszaköszön.
Mivel a Titu-lemmában a bal oldal számlálóiban az  számok négyzete szerepel, ezért bővítsük a Nesbitt-egyenlőtlenség bal oldalán szereplő törteket az alábbi módon, majd alkalmazzuk a Titu-lemmát:
számok négyzete szerepel, ezért bővítsük a Nesbitt-egyenlőtlenség bal oldalán szereplő törteket az alábbi módon, majd alkalmazzuk a Titu-lemmát:
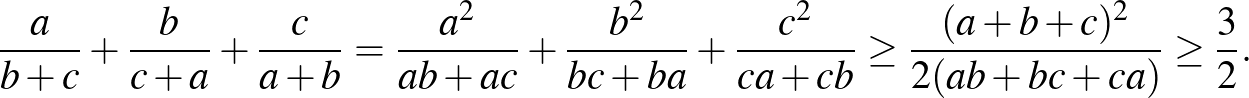
Az utolsó lépésnél felhasználtuk a második feladatsor 3. feladatát, vagyis azt, hogy 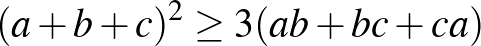 .
.
Néhány feladat CBS-re és a Titu-lemmára
1. Bizonyítsuk be, hogy bármely  ,
,  ,
,  pozitív valós szám esetén fennáll a
pozitív valós szám esetén fennáll a
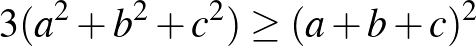
egyenlőtlenség. ([1] 35. oldal)
2. Legyen 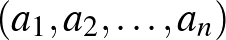 valós szám-
valós szám- -es, ahol nem minden
-es, ahol nem minden  nulla. Bizonyítsuk be, hogy ekkor
nulla. Bizonyítsuk be, hogy ekkor
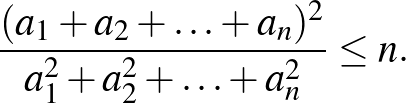
([1] 36. oldal)
3. Bizonyítsuk be, hogy ha  ,
,  ,
,  három olyan pozitív valós szám, amelyek szorzata 2, akkor
három olyan pozitív valós szám, amelyek szorzata 2, akkor 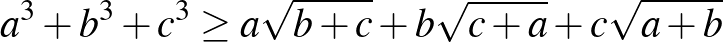 . (A Junior Balkan Mathematical Olympiad (JBMO 2002. Shortlist) feladata. ([2] 96. oldal)
. (A Junior Balkan Mathematical Olympiad (JBMO 2002. Shortlist) feladata. ([2] 96. oldal)
4. Bizonyítsuk be, hogy ha  ,
,  és
és  pozitív valós szám, akkor
pozitív valós szám, akkor
a) 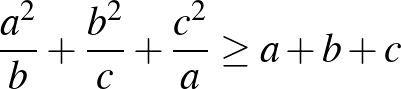 ; ([1] 175. oldal)
; ([1] 175. oldal)
b)  . (JBMO 2002 Shortlist, [1] 175. oldal)
. (JBMO 2002 Shortlist, [1] 175. oldal)
5. Bizonyítsuk be, hogy bármely  ,
,  ,
,  pozitív valós szám esetén teljesül az
pozitív valós szám esetén teljesül az
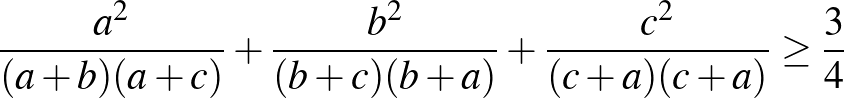
egyenlőtlenség. ([2] 101. oldal)
6. Bizonyítsuk be, hogy az  ,
,  ,
,  pozitív valós számok esetén
pozitív valós számok esetén
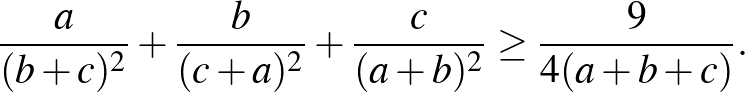
([1] 39. oldal)
7. Bizonyítsuk be, hogy bármely pozitív  ,
,  ,
,  szám esetén
szám esetén
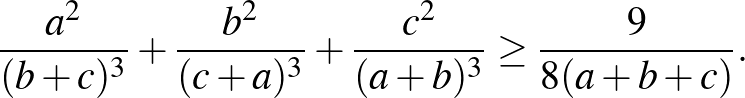
([2] 127. oldal)
8. Legyen  ,
,  ,
,  ,
, 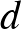 pozitív számnégyes. Bizonyítsuk be, hogy ekkor
pozitív számnégyes. Bizonyítsuk be, hogy ekkor
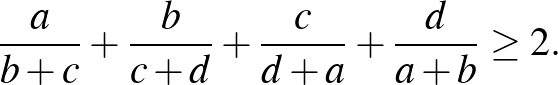
([1] 41. oldal)
9.* Bizonyítsuk be, hogy tetszőleges  ,
,  ,
,  ,
, 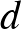 ,
,  pozitív valós számokra fennáll az
pozitív valós számokra fennáll az
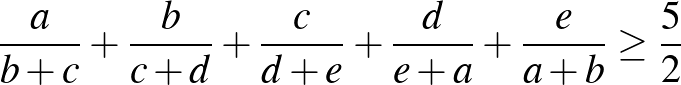
egyenlőtlenség! ([1] 176. oldal)
10. Bizonyítsuk be, hogy ha az  ,
,  ,
,  pozitív valós számokra teljesül az
pozitív valós számokra teljesül az 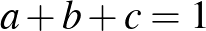 egyenlőség, akkor
egyenlőség, akkor
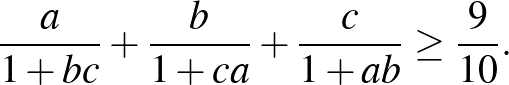
(Indiai versenyfeladat, [2] 101. oldal)
Hatványközepek közötti egyenlőtlenség
Az eddigi gondolatkörhöz szervesen kapcsolódik a hatványközepek témaköre. Helyhiány miatt most nem megyünk bele az általános fogalmakba és összegfüggésekbe. Az ezzel kapcsolatos részletek megtalálhatók az [1] V. fejezetében. Mivel a négy darab kéttagú közép mellett nagyon sokszor használjuk a háromtagú kiterjesztésüket, ezért felvázolok egy lehetséges utat az ezek közötti összefüggések bizonyítására.
Először igazoljuk a háromtagú számtani (aritmetikai) és mértani (geometriai) közép közötti egyenlőtlenséget, azaz
![$\displaystyle A(X_{3})=\frac{x+y+z}{3} \ge \sqrt[{3}]{xyz} =G\left(X_{3} \right),
$](/images/stories/latexuj/2025-01/2025-01-nevezetesegyenlotlensegek/img81.png)
ahol 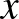 ,
, 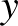 ,
, 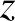 pozitív valós számok.
pozitív valós számok.
Ehhez használjuk fel a – kijelölt műveletek elvégzésével könnyen igazolható –
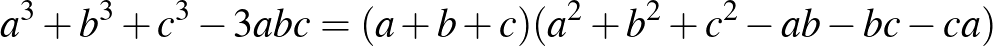
egyenlőséget. Az első feladatsor 3. feladata alapján tudjuk, hogy
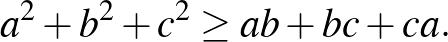
Használjuk ezt arra az esetre, ha  ,
,  ,
,  pozitív valós számok, ekkor
pozitív valós számok, ekkor 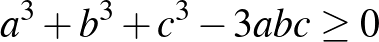 , azaz
, azaz 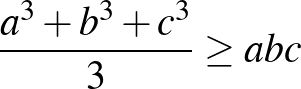 . Ha bevezetjük az
. Ha bevezetjük az  ,
,  ,
, 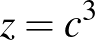 jelöléseket, akkor kapjuk a bizonyítandó egyenlőtlenséget. Egyenlőség akkor és csak akkor áll fenn, ha
jelöléseket, akkor kapjuk a bizonyítandó egyenlőtlenséget. Egyenlőség akkor és csak akkor áll fenn, ha 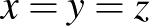 .
.
Ennek felhasználásával már könnyen bizonyítható a háromtagú harmonikus és mértani közép közötti egyenlőtlenség is, hiszen
![$\displaystyle H(X_{3})=\dfrac{1}{\dfrac{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}{3}...
...}]{\dfrac{1}{x}\cdot\dfrac{1}{y}\cdot\dfrac{1}{z}}}=\sqrt[{3}]{xyz}=G(X_{3}).
$](/images/stories/latexuj/2025-02/2025-02-potkepletnevezetesegyenlotlensegek/img2.png)
A háromtagú négyzetes (kvadratikus 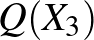 ) és számtani közép közötti egyenlőtlenség pedig következik az előző feladatsor 1. feladatából.
) és számtani közép közötti egyenlőtlenség pedig következik az előző feladatsor 1. feladatából.
Természetesen ezek kiterjeszthetők  (
(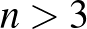 ) tagra is. A
) tagra is. A 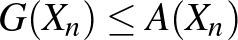 például a Cauchy-féle teljes indukcióval bizonyítható (lásd [1] 59. oldal), a
például a Cauchy-féle teljes indukcióval bizonyítható (lásd [1] 59. oldal), a 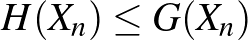 és az
és az 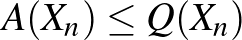 pedig az előzőekben látott gondolatmenetekkel.
pedig az előzőekben látott gondolatmenetekkel.
Feladatok hatványközepekre
1. Bizonyítsuk be, hogy ha  ,
,  ,
,  pozitív valós számok, akkor fennállnak az alábbi egyenlőtlenségek:
pozitív valós számok, akkor fennállnak az alábbi egyenlőtlenségek:
a) 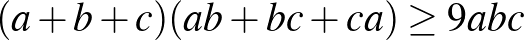 ; ([1] 184. oldal)
; ([1] 184. oldal)
b) 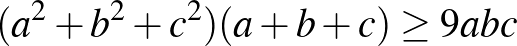 ; ([1] 184. oldal)
; ([1] 184. oldal)
c) 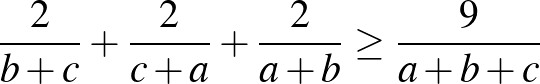 . ([1] 66. oldal)
. ([1] 66. oldal)
2. Legyenek  ,
,  ,
,  pozitív valós számok. Bizonyítsuk be, hogy ekkor
pozitív valós számok. Bizonyítsuk be, hogy ekkor

([1] 185. oldal)
3. Bizonyítsuk be, hogy ha az  ,
,  ,
,  pozitív valós számok szorzata 1, akkor
pozitív valós számok szorzata 1, akkor
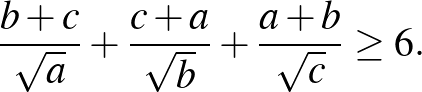
([2] 68. oldal)
4. Egy 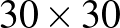 -as négyzet négy sarkából vágjunk le egybevágó négyzeteket úgy, hogy a lap négy szélének a felhajtásával a lehető legnagyobb térfogatú dobozt kapjuk! Mekkorák az így keletkező doboz méretei? ([1] 71. oldal)
-as négyzet négy sarkából vágjunk le egybevágó négyzeteket úgy, hogy a lap négy szélének a felhajtásával a lehető legnagyobb térfogatú dobozt kapjuk! Mekkorák az így keletkező doboz méretei? ([1] 71. oldal)
5. Milyen méretei vannak a legkisebb felszínű 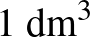 térfogatú, henger alakú konzervdoboznak? ([1] 72. oldal)
térfogatú, henger alakú konzervdoboznak? ([1] 72. oldal)
6. Bizonyítsuk be, hogy ha  ,
,  ,
,  pozitív valós számok, akkor
pozitív valós számok, akkor
a)  ;
;
b) 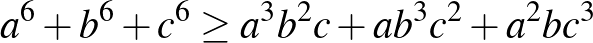 .
.
([1] 72. oldal)
7. Legyenek 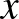 ,
, 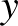 ,
, 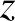 pozitív valós számok. Bizonyítsuk be, hogy ekkor
pozitív valós számok. Bizonyítsuk be, hogy ekkor
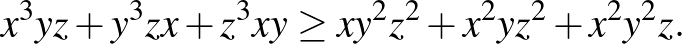
([1] 187. oldal)
8. Bizonyítsuk be, hogy ha  pozitív egész szám, akkor fennállnak az alábbi egyenlőtlenségek:
pozitív egész szám, akkor fennállnak az alábbi egyenlőtlenségek:
a) 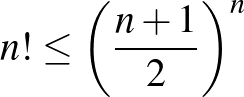 ;
;
b) 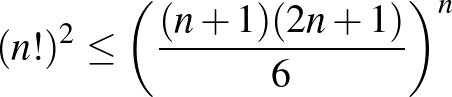 ;
;
c) 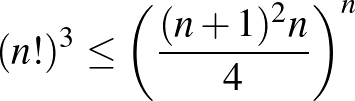 ;
;
d) ![$8\sqrt[{n}]{(3n)!} <(3n+1)^3$](/images/stories/latexuj/2025-01/2025-01-nevezetesegyenlotlensegek/img108.png) . ([2] 78. oldal)
. ([2] 78. oldal)
9. Legyen  2-nél nagyobb egész szám. Bizonyítsuk be, hogy ekkor
2-nél nagyobb egész szám. Bizonyítsuk be, hogy ekkor
![$\displaystyle n\sqrt[{n}]{n+1} -n\le 1+\frac{1}{2}+\ldots+\frac{1}{n} \le n-\frac{n-1}{\sqrt[{n-1}]{n}}.
$](/images/stories/latexuj/2025-01/2025-01-nevezetesegyenlotlensegek/img109.png)
([2] 80. oldal)
Rendezési tétel (Szűcs Adolf tétele), Csebisev-egyenlőtlenség
Tapasztalatom szerint a fiatalok előszeretettel használják a rendezési tételt. Ezért is döntöttem úgy, hogy említést teszek róla ebben az összeállításban.
Mikor nevezünk két szám- -est azonosan, illetve ellentétesen rendezettnek?
-est azonosan, illetve ellentétesen rendezettnek?
Legyen 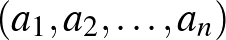 és
és 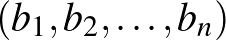 két valós szám-
két valós szám- -es. A két szám-
-es. A két szám- -es azonosan (ellentétesen) rendezett, ha bármely
-es azonosan (ellentétesen) rendezett, ha bármely 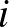 -re és
-re és  -re (
-re (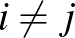 )
) 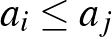 -ből következik, hogy
-ből következik, hogy 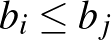 (
(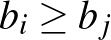 ).
).
A rendezési tétel pedig a következő:
Legyen 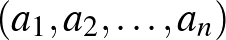 és
és 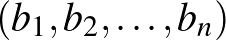 két valós szám-
két valós szám- -es. Legyen továbbá
-es. Legyen továbbá 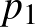 ,
, 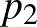 ,
,  ,
, 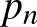 a
a 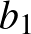 ,
, 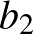 ,
,  ,
, 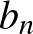 egy permutációja. Az
egy permutációja. Az 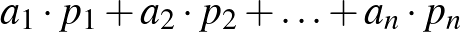 kifejezés értéke akkor maximális (minimális), ha az
kifejezés értéke akkor maximális (minimális), ha az 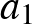 ,
, 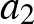 ,
,  ,
, 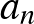 és
és 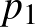 ,
, 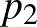 ,
,  ,
, 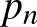 szám-
szám- -es azonosan (ellentétesen) rendezett.
-es azonosan (ellentétesen) rendezett.
A tétel bizonyítása megtalálható az [1] 49. oldalán.
Feladatok rendezési tételre és Csebisev-egyenlőtlenségre
1. Bizonyítsuk be, hogy ha  ,
,  ,
,  pozitív valós számok, akkor fennállnak az alábbi egyenlőtlenségek:
pozitív valós számok, akkor fennállnak az alábbi egyenlőtlenségek:
a) 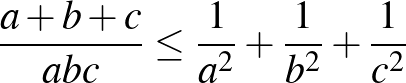 ;
;
b) 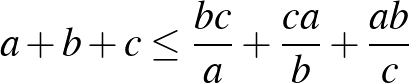 . ([1] 51. oldal)
. ([1] 51. oldal)
2. Bizonyítsuk be, hogy ha  ,
,  ,
,  pozitív valós számok, akkor fennállnak az alábbi egyenlőtlenségek:
pozitív valós számok, akkor fennállnak az alábbi egyenlőtlenségek:
a) 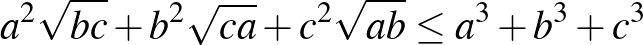 ; ([1] 179. oldal)
; ([1] 179. oldal)
b) 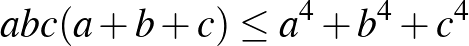 . ([1] 179. oldal)
. ([1] 179. oldal)
3. Legyenek  ,
,  ,
,  pozitív valós számok,
pozitív valós számok,  pedig pozitív egész szám! Bizonyítsuk be, hogy ekkor
pedig pozitív egész szám! Bizonyítsuk be, hogy ekkor
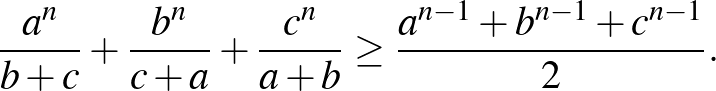
([1] 53. oldal)
4. Bizonyítsuk be, hogy ha  ,
,  ,
,  pozitív valós számok, akkor
pozitív valós számok, akkor
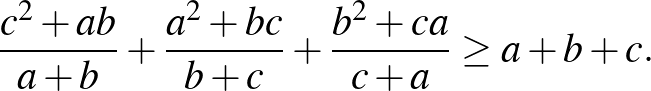
([1] 180. oldal)
5. Bizonyítsuk be, hogy ha az  ,
,  ,
,  pozitív valós számok összege 3, akkor
pozitív valós számok összege 3, akkor
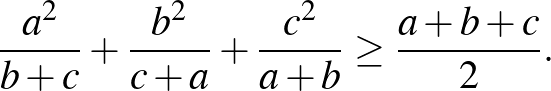
([2] 60. oldal)
6. Igazoljuk, hogy ha  ,
,  ,
,  pozitív valós számok, akkor
pozitív valós számok, akkor
a) 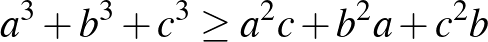 ;
;
b) 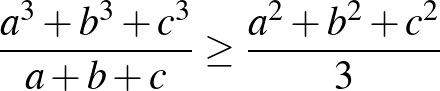 . ([2] 62. oldal)
. ([2] 62. oldal)
7. Bizonyítsuk be, hogy ha  ,
,  ,
,  ,
, 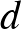 pozitív valós számok, akkor
pozitív valós számok, akkor
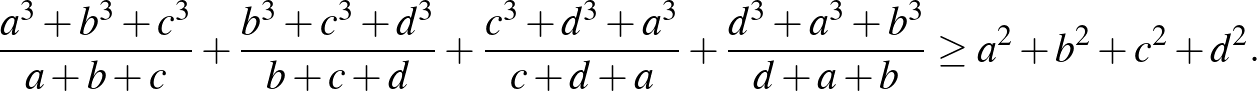
([2] 63. oldal)
8. Legyen 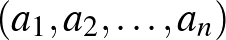 és
és 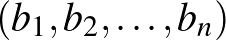 két valós szám-
két valós szám- -es. Ha a két szám-
-es. Ha a két szám- -es azonosan rendezett, akkor
-es azonosan rendezett, akkor
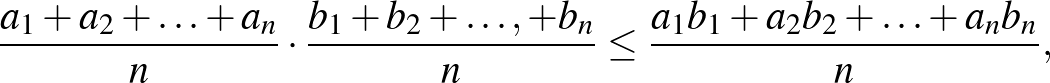
ha ellentétesen rendezett, akkor
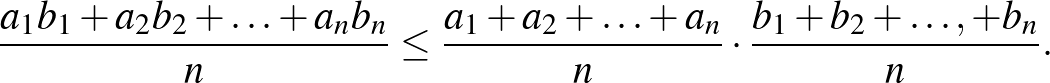
(Csebisev-egyenlőtlenség, [1] 50. oldal)
9. Legyen 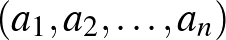 pozitív valós szám-
pozitív valós szám- -es és
-es és 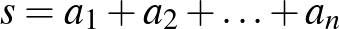 . Bizonyítsuk be, hogy ekkor
. Bizonyítsuk be, hogy ekkor
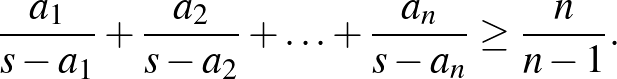
([1] 181. oldal)
10. Legyen  pozitív valós szám-
pozitív valós szám- -es. Bizonyítsuk be, hogy ekkor
-es. Bizonyítsuk be, hogy ekkor
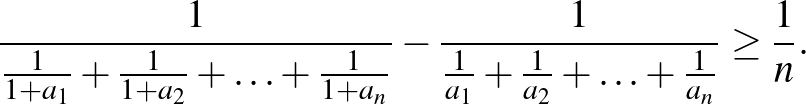
([1] 182. oldal)
Összetett alkalmazások és további módszerek
Ebben a részben megoldunk két nehezebb feladatot, amelyeknél az eddig látottakat alkalmazzuk további trükkökkel kiegészítve. Az egyenlőtlenségek megoldásánál jól használható, célravezető helyettesítések és módszerek gyűjteménye megtalálható az [1] VIII. fejezetében.
1. Bizonyítsuk be, hogy ha az  ,
,  ,
,  pozitív valós számok szorzata 1, akkor
pozitív valós számok szorzata 1, akkor
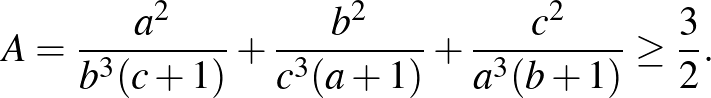
Megoldás. Ha az egyenlőtlenségben szereplő ismeretlenek szorzata 1, akkor hasznos lehet az alkalmasan megválasztott 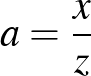 ,
, 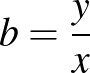 ,
, 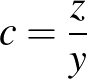 helyettesítés. Ezt felhasználva a bal oldalra kapjuk, hogy
helyettesítés. Ezt felhasználva a bal oldalra kapjuk, hogy
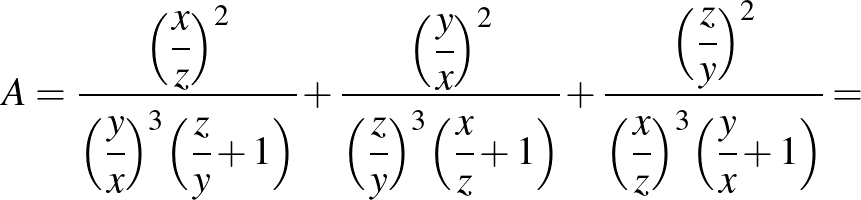 |
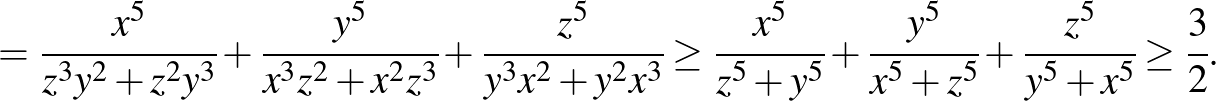 |
Itt felhasználtuk, hogy 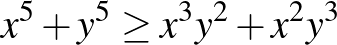 és ennek megfelelő változatait, amely többek között rendezési tétellel könnyen bizonyítható, az utolsó lépésnél pedig a Nesbitt-egyenlőtlenséget alkalmaztuk. Egyenlőség akkor és csak akkor áll fenn, ha
és ennek megfelelő változatait, amely többek között rendezési tétellel könnyen bizonyítható, az utolsó lépésnél pedig a Nesbitt-egyenlőtlenséget alkalmaztuk. Egyenlőség akkor és csak akkor áll fenn, ha 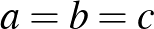 . Ezzel a feladatot megoldottuk.
. Ezzel a feladatot megoldottuk.
2. Bizonyítsuk be, hogy ha az  ,
,  ,
,  pozitív valós számok szorzata 1, akkor
pozitív valós számok szorzata 1, akkor
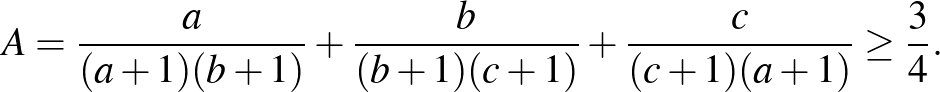
(IMO Shortlist 1998.)
Megoldás. Használjuk megint az előző feladatban látott helyettesítést, azaz 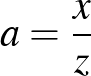 ,
, 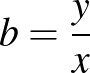 ,
, 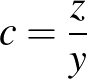 . Ekkor
. Ekkor
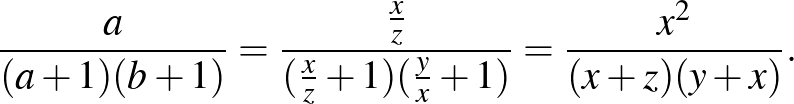
A többi tagra is hajtsuk végre ezt az átalakítást, majd alkalmazzuk a Titu-lemmát. Így kapjuk, hogy
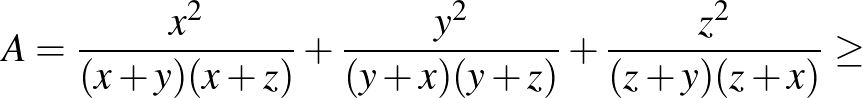 |
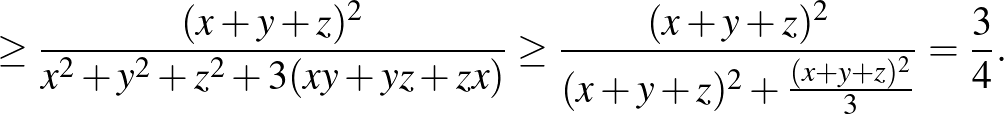 |
Az utolsó lépésnél felhasználtuk az első feladatsor 4. feladatát, amely szerint
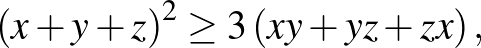
azaz
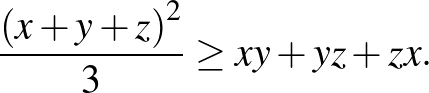
Végiggondolható, hogy egyenlőség akkor és csak akkor áll fenn, ha 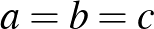 . Ezzel a feladatot megoldottuk.
. Ezzel a feladatot megoldottuk.
Talán a jelen cikk is érzékelteti, hogy mennyire szerteágazó és összetett a nevezetes egyenlőtlenségek témaköre. Itt csak néhány fontosabb egyenlőtlenség és megoldási módszer bemutatására volt lehetőség. Ha valaki szeretne jobban elmélyülni ebben a témakörben, annak ajánlom a cikk végén felsorolt szakirodalmakat. Ezek közül az [1]-ben és [2]-ben a részletes elmélet mellett több száz feladatot és azok megoldását is megtalálja az érdeklődő olvasó.
Hivatkozások
- [1] Ábrahám Gábor (2017): Egyenlőtlenségek I., Zalai Matematikai Tehetségekért Alapítvány, Nagykanizsa
[2] Ábrahám Gábor (2018): Egyenlőtlenségek II., Matematikai Tehetségekért Alapítvány, Nagykanizsa
[3] Schultz János (2009): 111 feladat algebrai egyenlőtlenségekre (Matematikai oktatási portál) Letöltés:
https://matek.fazekas.hu/index.php?option=com_content&view=article&id=344:schultz-janos-111-feladat-algebrai-egyenlotlensegekre&catid=21&Itemid=136
Szegedi Radnóti Miklós Kísérleti Gimnázium











