Az elemi matematikában számomra mindig azok a legizgalmasabb feladatok, amelyek megoldásához valamely látszólag nem odaillő terület ismereteit használjuk. Ismerjük algebrai feladatoknak például geometriai vagy függvénytani interpretációját. Nagyon inspirálók voltak ilyen tekintetben a speciális matematika tagozaton tanító tanárok számára évente megrendezésre kerülő ún. specmat-találkozók, ahol elsősorban Hraskó András tanár úr ilyen kiegészítéseit hallhattuk a megtekintett bemutatóórák után. Ez a cikk is ezen motiváló tényezők hatására született.
A következőkben néhány, a koordinátarácson megoldható feladattal ismerkedünk meg. Ezek egy része megfogalmazásában is tartalmazza a rácsot, mások megoldásához pedig úgy jutunk el, ha egy rácson jelenítjük meg, ezáltal a matematika több területét kapcsoljuk össze. A témát bizonyos formában már feldolgoztam a 2008-as debreceni Rátz László Vándorgyűlésen tartott feladatmegoldó szemináriumon. Az akkor elhangzott feladatok egy részét megtartottam, frissítettem és újakkal egészítettem ki.
Úgy gondolom, hogy a bemutatott példák jól használhatók tehetséggondozó-szakköröket tartó tanárok számára, de akár tanórákon is bevethetők matematikából haladóbb szinten álló tanulócsoportok esetén. Ugyanakkor jó gondolatébresztők is lehetnek újabb feladatok kitűzése során.
1. Egy csiga a koordináta-rendszer origójából indul, és az ábrán látható mintának megfelelően folytatja útját. Másodpercenként 1 egységet tesz meg. Melyik pontban lesz egy, illetve két órával az indulás után?
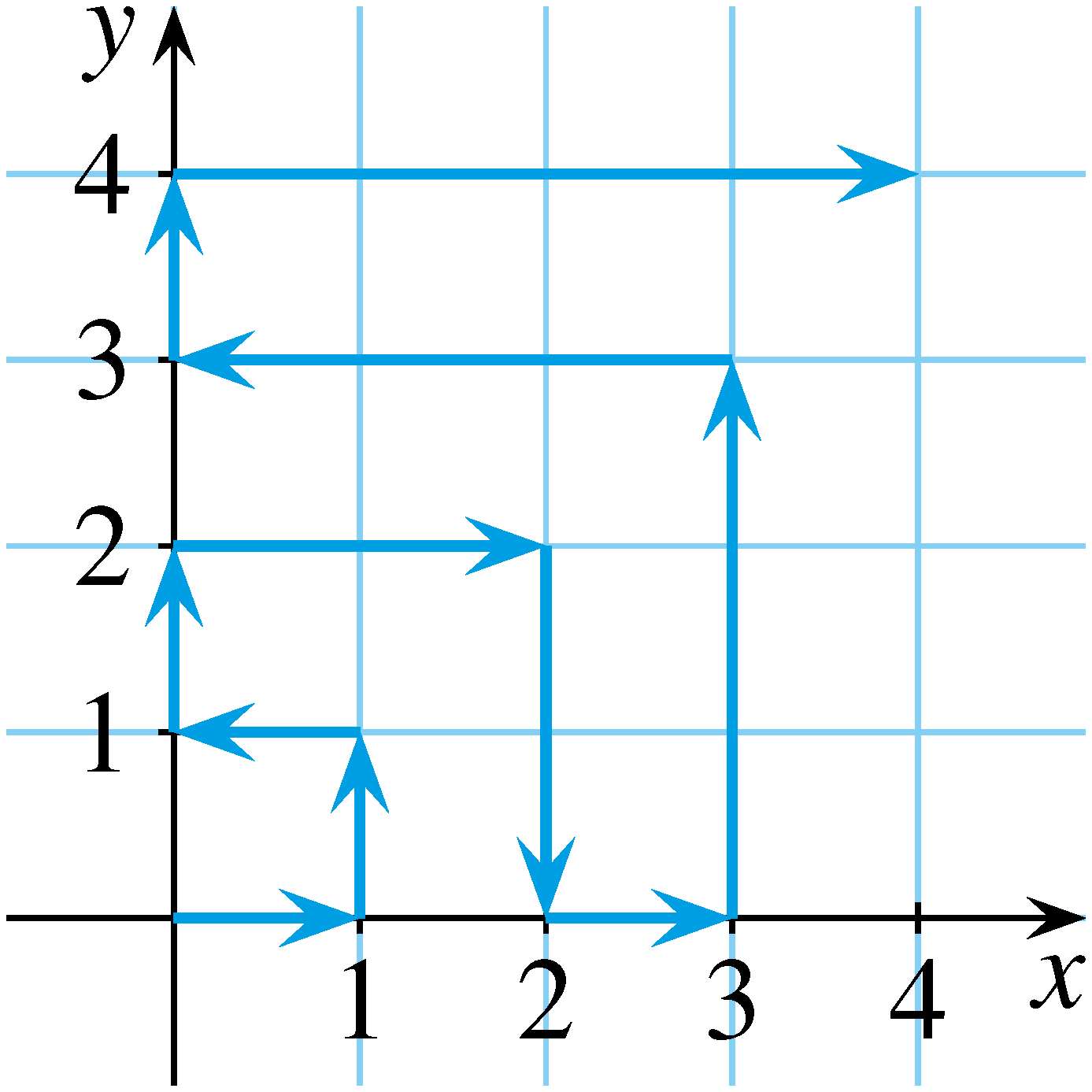
Megoldás. Készítsünk rajzot! Írjuk fel a „kanyarokba” az ott-tartózkodás időpontját!
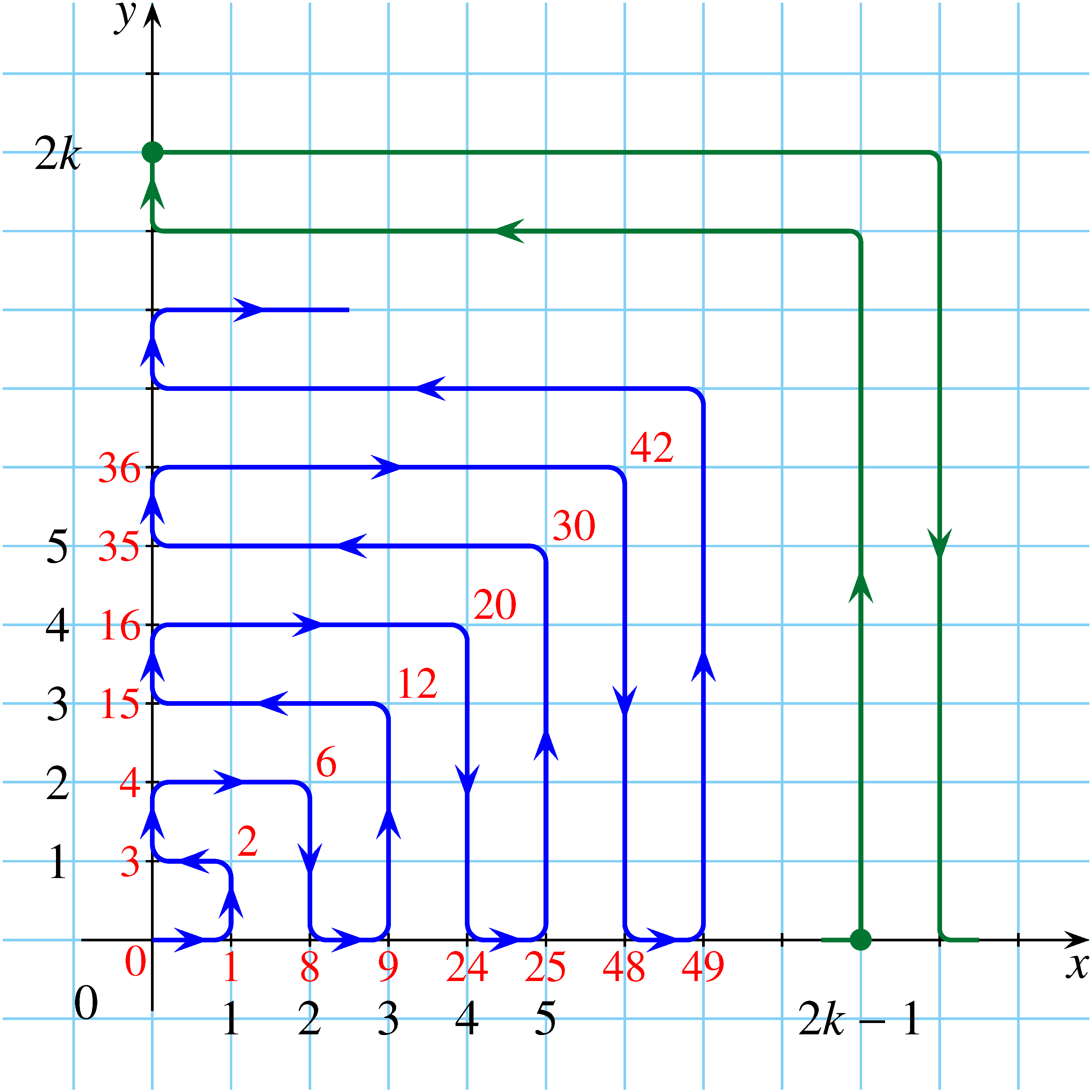
Az ábra alapján a következő sejtésünk fogalmazható meg:
A csiga a 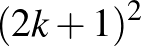 időpontban a koordináta-rendszer
időpontban a koordináta-rendszer 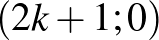 pontjában, míg a
pontjában, míg a 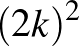 időpontban a
időpontban a 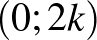 pontjában tartózkodik. Ez teljes indukcióval könnyen bizonyítható.
pontjában tartózkodik. Ez teljes indukcióval könnyen bizonyítható.
Tehát a csiga 1 óra (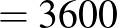 s) eltelte után a
s) eltelte után a 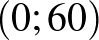 pontban lesz, és bármely időpont esetén csak azt kell megnézni, hogy az melyik két négyzetszám közé esik. Ez alapján ugyanis a tartózkodási hely könnyen meghatározható. Mivel
pontban lesz, és bármely időpont esetén csak azt kell megnézni, hogy az melyik két négyzetszám közé esik. Ez alapján ugyanis a tartózkodási hely könnyen meghatározható. Mivel 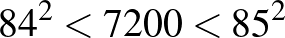 , továbbá
, továbbá 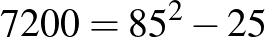 , így tehát két óra, azaz 7200 másodperc elteltével a
, így tehát két óra, azaz 7200 másodperc elteltével a 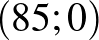 ponttól 25 lépéssel „visszafelé”, a
ponttól 25 lépéssel „visszafelé”, a 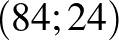 pontban lesz a csiga.
pontban lesz a csiga.
2. Bizonyítsuk be, hogy bármely 5 rácspont között van kettő, amelyek összekötő szakasza átmegy egy további rácsponton!
Megoldás. Osztályozzuk a rácspontokat koordinátáik paritása szerint. Négy ilyen osztály lesz (páros–páros, páros–páratlan, páratlan–páros, páratlan–páratlan). Mivel a pontok száma 5, így a skatulyaelv szerint szükségképpen van legalább két azonos osztályba eső pont. Világos, hogy az ezen pontok által meghatározott szakasz felezőpontja is rácspont, amivel az állítást beláttuk.
3. Egy sakktáblát átszelő egyenes legfeljebb hány mező belsején mehet keresztül?
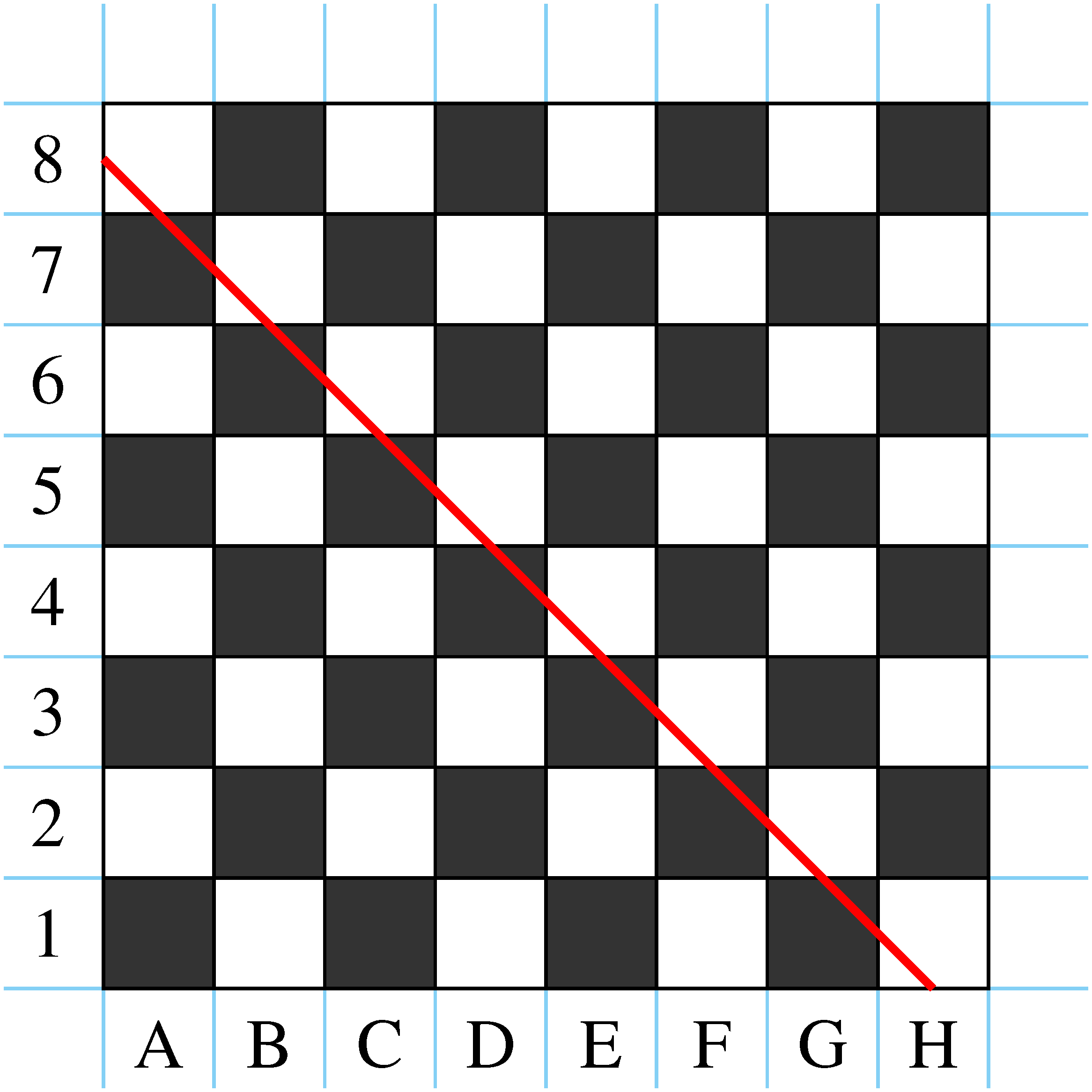
Megoldás. A táblán 9 „vízsés vagy az utolsó, vagy az utolsó előtti metszéspontnál lép kizintes” és 9 „függőleges” rácsegyenes található. A vízszintes és függőleges rácsegyenesek is 8-8, egységnyi szélességű sávot hoznak létre. Egy tetszőleges „ferde” egyenes mind a 18 rácsegyenest metszi, csak nem biztos, hogy a sakktábla belsejében vagy határán. Tekintsünk egy tetszőleges egyenest, amely valahol „belép” a sakktáblára. Számoljuk össze az innen rajta keletkező metszéspontokat. Ez tehát legfeljebb 18, amely 17 szakaszra és két félegyenesre osztja egyenesünket. A szakaszokkal számolhatjuk az egyenes által átszelt mezőket: két szomszédos metszéspont által meghatározott szakasz, amelynek belső pontjai a tábla belsejébe esnek, egy átszelt mezőt jelent. Akkor lép be egyenesünk a sakktábla belsejébe, ha mindkét irányú határegyenest metszett, és vagy az utolsó, vagy az utolsó előtti metszéspontnál lép ki. Ha egyszerre metszi a két határegyenest, akkor a metszéspontok száma kevesebb. 18 metszéspont úgy keletkezhet, ha nincs olyan metszéspont, amelyben egyszerre két rácsegyenest is metsz az egyenesünk. Ekkor 17 szakasz keletkezik, amelyek közül legalább kettő (egy belépéskor, egy kilépéskor) a táblán kívül helyezkedik el. 17 metszéspont úgy keletkezhet, hogy az egyenes a tábla egyik csúcsán átmegy (pl. a bal felső csúcson) és itt egyszerre két rácsegyenest metsz. Ekkor 16 szakasz keletkezik, amelyek közül legalább egy a táblán kívül helyezkedik el. Ha úgy helyezkedik el az egyenes, hogy a metszéspontok száma 17-nél kevesebb, akkor a keletkező szakaszok száma legfeljebb 15 (és ezek közül nem is mind van feltétlenül a tábla belsejében). Az egyenes által átszelt mezők száma tehát legfeljebb 15. Ez elő is fordulhat, ha pl. az átlót eltoljuk vízszintesen fél négyzetegységgel.
Az alábbi feladat hasonló a 3. feladathoz, csak térbeli gondolkodást igényel (a szerző által kitűzött feladat volt a 2005. évi Nemzetközi Magyar Matematikaversenyen).
4. Egységnyi élű fakockákból téglatestet építettünk, amelynek a méretei 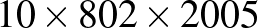 . Hány egységkockát lyukaszt ki az a pontszerű szú, amelyik a téglatest egyik testátlója mentén végigrágja magát?
. Hány egységkockát lyukaszt ki az a pontszerű szú, amelyik a téglatest egyik testátlója mentén végigrágja magát?
Megoldás. Helyezzük a térbeli koordináta-rendszer origóját a téglatest egyik csúcsába! Legyen a „start” csúcsból kiinduló 3 él a 3 koordinátatengely pozitív fele.
Jellemezzük az egységkockákat az origótól legtávolabbi csúcsuk koordinátáival! A „start” kocka így az 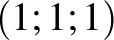 , a „cél” pedig a
, a „cél” pedig a 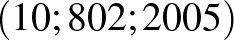 .
.
Minden „határátlépés” (a továbbiakban röviden: lépés) során új kockába jut a szú, mégpedig
– csúcson (ekkor mindhárom koordináta nő),
– élen, de nem csúcson (ekkor 2 koordináta nő),
– lapon, de nem élen (ekkor pedig 1 koordináta nő).
Csúcson akkor lép át a szú, ha van az eredetihez hasonló rész-téglatest. Mivel 10, 802 és 2005 legnagyobb közös osztója 1, így ilyen eset nem fordulhat elő.
Az éleken történő áthaladások meghatározásához vizsgáljuk meg a különböző koordinátasíkokra eső merőleges vetületeket. Ekkor a téglatest lapjai egy-egy téglalapot, a síkra merőleges élek pedig ezekben a téglalapokban rácspontokat határoznak meg. Amikor a szú a térben egy élen áthalad, az vetületileg egy rácsponton történő átmenetelt jelent. A 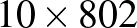 -es téglalaphoz hasonló legkisebb téglalap az
-es téglalaphoz hasonló legkisebb téglalap az 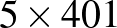 -es téglalap. A szú a mozgása során két ilyen téglalapot érint (hiszen a hasonlóság aránya 2), ami 1 lépést jelent. Hasonlóan kapjuk, hogy a
-es téglalap. A szú a mozgása során két ilyen téglalapot érint (hiszen a hasonlóság aránya 2), ami 1 lépést jelent. Hasonlóan kapjuk, hogy a 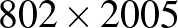 -ös téglalap esetén (amelyhez hasonló legkisebb téglalap
-ös téglalap esetén (amelyhez hasonló legkisebb téglalap 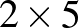 -ös) 400, míg a
-ös) 400, míg a 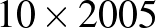 -ös esetén (amelyhez pedig a
-ös esetén (amelyhez pedig a 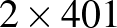 -es legkisebb téglalap tartozik) 4 lépést tesz meg a szú. Az éleken való áthaladás tehát
-es legkisebb téglalap tartozik) 4 lépést tesz meg a szú. Az éleken való áthaladás tehát 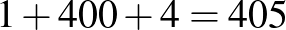 lépést, azaz 810 koordinátaváltozást jelent.
lépést, azaz 810 koordinátaváltozást jelent.
Mivel a koordináták összváltozása 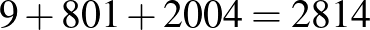 , amelyből 810 az előzőek értelmében éleken való áthaladás miatt történik, így
, amelyből 810 az előzőek értelmében éleken való áthaladás miatt történik, így 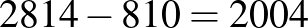 lépés történik csak lapon.
lépés történik csak lapon.
Az összes lépés száma 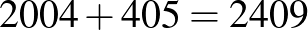 , így a bejárt egységkockák száma 2410.
, így a bejárt egységkockák száma 2410.
Megjegyzés. Eredményünk a, b, c oldalú téglatestre általánosítva szép szitaformulát eredményez: 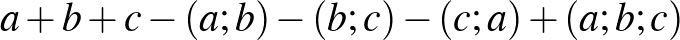 , ahol a zárójeles kifejezések (szokásosan) a bennük szereplő számok legnagyobb közös osztóját jelentik.
, ahol a zárójeles kifejezések (szokásosan) a bennük szereplő számok legnagyobb közös osztóját jelentik.
Esetünkben: 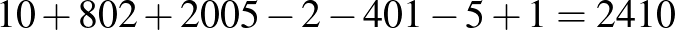 , ami összhangban van a fent kapott eredménnyel.
, ami összhangban van a fent kapott eredménnyel.
5. Hányféleképpen juthatunk az origóból az 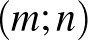 pontba (ahol
pontba (ahol 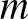 és
és 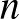 egyaránt pozitív egész), ha egy lépésben csak jobbra vagy felfelé haladhatunk egységnyit?
egyaránt pozitív egész), ha egy lépésben csak jobbra vagy felfelé haladhatunk egységnyit?
Megoldás. Minden lépés az egyik koordinátát 1-gyel növeli. Így a lépések száma 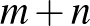 . Ebből
. Ebből 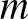 lépés jobbra,
lépés jobbra, 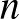 pedig felfelé történik. Ezek száma pedig
pedig felfelé történik. Ezek száma pedig 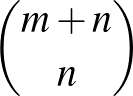 .
.
6. Egy 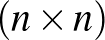 -es sakktábla széttörött úgy, hogy a mellékátlója által átszelt mezők és az ez alatti rész maradt épen. Hányféleképpen juthatunk el a bal alsó mezőről (
-es sakktábla széttörött úgy, hogy a mellékátlója által átszelt mezők és az ez alatti rész maradt épen. Hányféleképpen juthatunk el a bal alsó mezőről (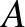 ) a jobb felső mezőre (
) a jobb felső mezőre (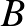 ) a sakktábla épen maradt mezőinek középpontjain felfelé és jobbra lépegetve?
) a sakktábla épen maradt mezőinek középpontjain felfelé és jobbra lépegetve?
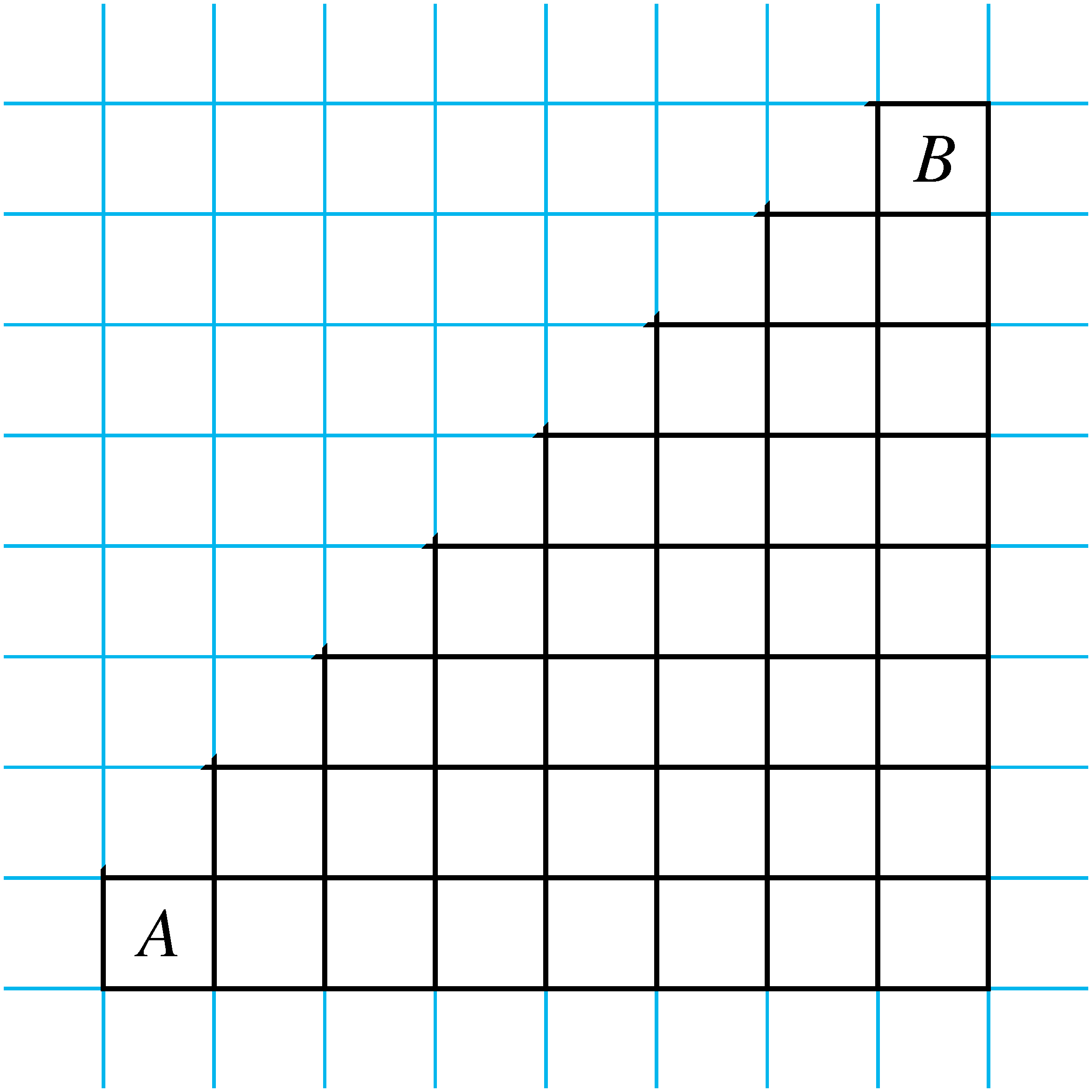
Megoldás. A „rossz” utakat fogjuk összeszámlálni. Egy út rossz, ha kivezet a sakktábla épen maradt részéből, azaz metszi az alábbi ábrán látható átlót.
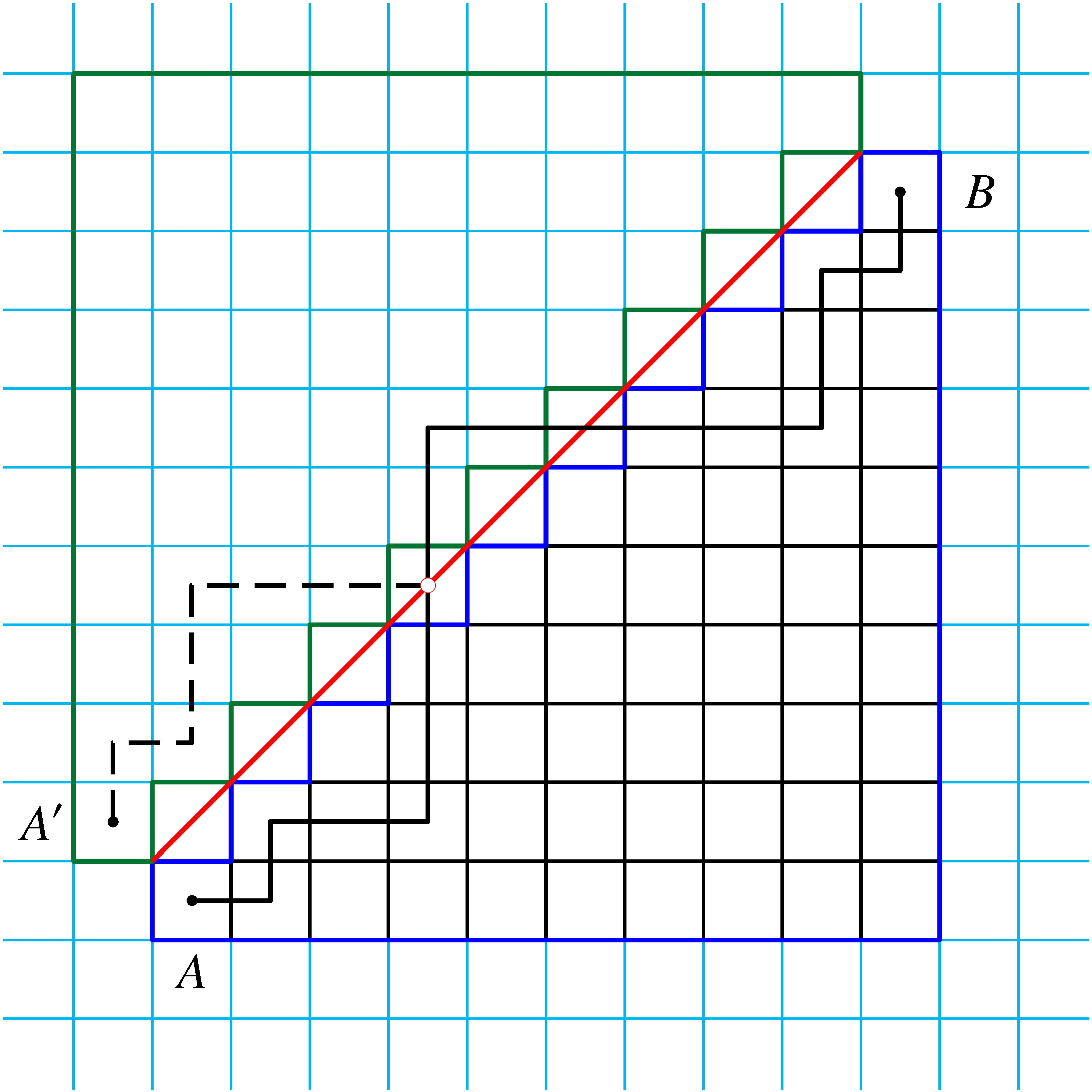
Tekintsünk egy „rossz” 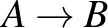 utat. Az
utat. Az 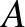 ponttól az átlóval való első metszéspontig terjedő útszakaszt tükrözzük az átlóra, ezáltal kapunk egy
ponttól az átlóval való első metszéspontig terjedő útszakaszt tükrözzük az átlóra, ezáltal kapunk egy 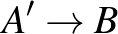 utat (lásd az ábrát). A „rossz” utak és az
utat (lásd az ábrát). A „rossz” utak és az 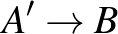 utak között kölcsönösen egyértelmű megfeleltetést létesít az említett tükrözés, ezért a „rossz” utak száma megegyezik az
utak között kölcsönösen egyértelmű megfeleltetést létesít az említett tükrözés, ezért a „rossz” utak száma megegyezik az 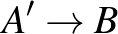 utakéval. Az összes
utakéval. Az összes 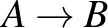 út számából kivonva az
út számából kivonva az 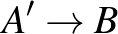 utak számát, megkapjuk az eredményt. Az
utak számát, megkapjuk az eredményt. Az 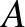 pontból a
pontból a 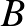 pontba
pontba 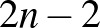 lépéssel jutunk el, amelyből
lépéssel jutunk el, amelyből 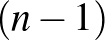 -szer jobbra,
-szer jobbra, 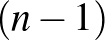 -szer felfelé lépünk. Felhasználva az 5. feladat eredményét, ezeknek az utaknak a száma
-szer felfelé lépünk. Felhasználva az 5. feladat eredményét, ezeknek az utaknak a száma 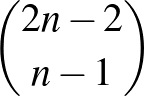 . Az
. Az 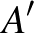 pontból a
pontból a 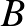 pontba szintén
pontba szintén 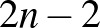 lépéssel jutunk el, amelyből
lépéssel jutunk el, amelyből 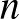 -szer lépünk jobbra, tehát az
-szer lépünk jobbra, tehát az 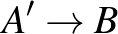 utak száma
utak száma 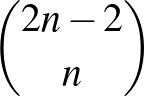 . Így a jó utak száma:
. Így a jó utak száma:
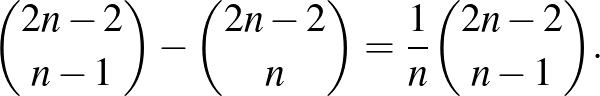
Megjegyzés. Ezek az úgynevezett Catalan-számok.
7. A negyedik feladatban szereplő téglatest egyik csúcsából az onnan induló testátló másik végpontjába egységnyi lépésekkel folyton közeledve hányféleképpen juthatunk el, ha csak a téglatest valamely élével párhuzamosan léphetünk, és az út során a téglatestből nem léphetünk ki?
Megoldás. Az origóból kell egységnyi koordinátatengely-irányú lépésekkel eljutni a 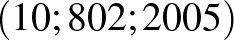 pontba. Egy ilyen utat leírhatunk egy 10 darab
pontba. Egy ilyen utat leírhatunk egy 10 darab 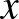 , 802 darab
, 802 darab 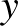 és 2005 darab
és 2005 darab 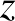 betűből álló 2817 hosszúságú jelsorozattal. Ezek száma a betűk ismétléses permutációinak száma:
betűből álló 2817 hosszúságú jelsorozattal. Ezek száma a betűk ismétléses permutációinak száma: 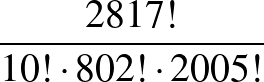 .
.
Ugyanerre az eredményre jutunk, ha a lehetséges 2817 lépés közül kiválasztjuk a 10 darab 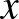 irányút, majd a maradékból a 802
irányút, majd a maradékból a 802 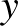 irányút:
irányút:
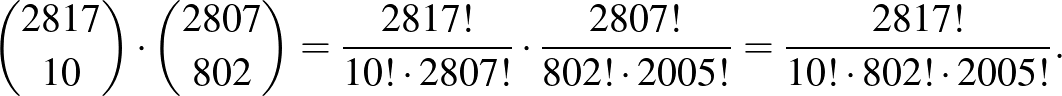
A következő (nem geometriai) feladatok megoldásánál segítségül hívjuk a négyzetrácsot.
8. A 2023-as női kézilabda világbajnokság döntőjében a francia válogatott Norvégia ellen a félidőben 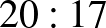 -re vezetett. Azt tudjuk még, hogy a végeredmény
-re vezetett. Azt tudjuk még, hogy a végeredmény 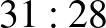 lett a franciák javára. Ezek ismeretében hányféleképpen alakulhatott a második félidőben a mérkőzés?
lett a franciák javára. Ezek ismeretében hányféleképpen alakulhatott a második félidőben a mérkőzés?
Megoldás. A feladat ekvivalens azzal, hogy hányféleképpen juthatunk el a 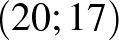 pontból a
pontból a 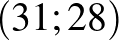 -ba, avagy eltolással a
-ba, avagy eltolással a 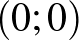 pontból a
pontból a 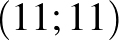 -be. Az 5. feladat alapján a válasz:
-be. Az 5. feladat alapján a válasz:  .
.
9. Bizonyítsuk be a következő összefüggéseket:
(a) 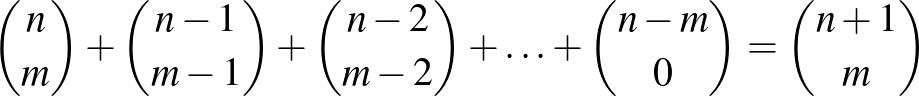 ;
;
(b) 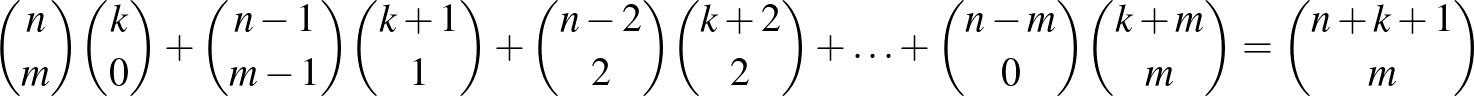 ;
;
(c) 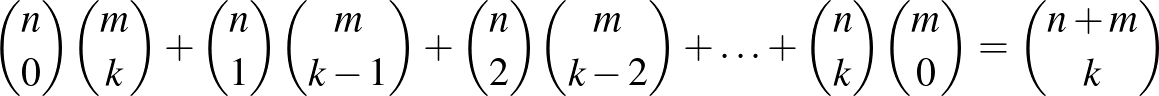 ,
,
ahol 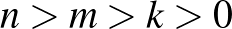 egész számok.
egész számok.
Megoldás. Mindhárom esetben a koordináta-rendszer 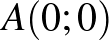 pontjából
pontjából 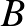 -be megyünk a már említett módon rácspontról rácspontra, jobbra vagy felfelé haladva.
-be megyünk a már említett módon rácspontról rácspontra, jobbra vagy felfelé haladva.

(a) Tegyük fel, hogy ez a 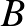 pont a
pont a 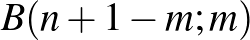 . Az 5. feladat értelmében az összes utak száma:
. Az 5. feladat értelmében az összes utak száma: 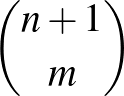 . Másrészt minden j-re (
. Másrészt minden j-re ( 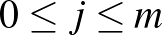 ) azon utak száma, amelyekben a
) azon utak száma, amelyekben a 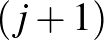 -edik lépésünk az első jobbra történő elmozdulás, vagyis az első j lépés után az
-edik lépésünk az első jobbra történő elmozdulás, vagyis az első j lépés után az 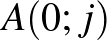 pontból indulunk tovább:
pontból indulunk tovább: 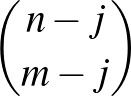 . Ezeket összegezve az összes lehetséges útvonalak száma valóban
. Ezeket összegezve az összes lehetséges útvonalak száma valóban
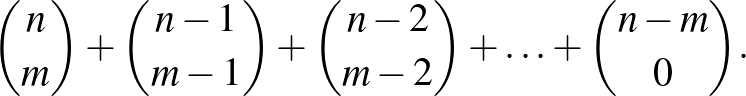
(b) Tekintsük most a következő ábrát! 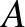 -ból
-ból 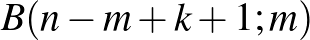 -be összesen
-be összesen 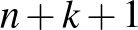 lépést kell tennünk, ebből
lépést kell tennünk, ebből 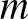 lépést felfelé,
lépést felfelé, 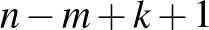 lépést jobbra. Az ilyen utak száma a fent említettek szerint
lépést jobbra. Az ilyen utak száma a fent említettek szerint 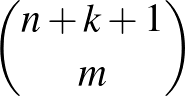 , ami az összefüggés jobb oldala.
, ami az összefüggés jobb oldala.
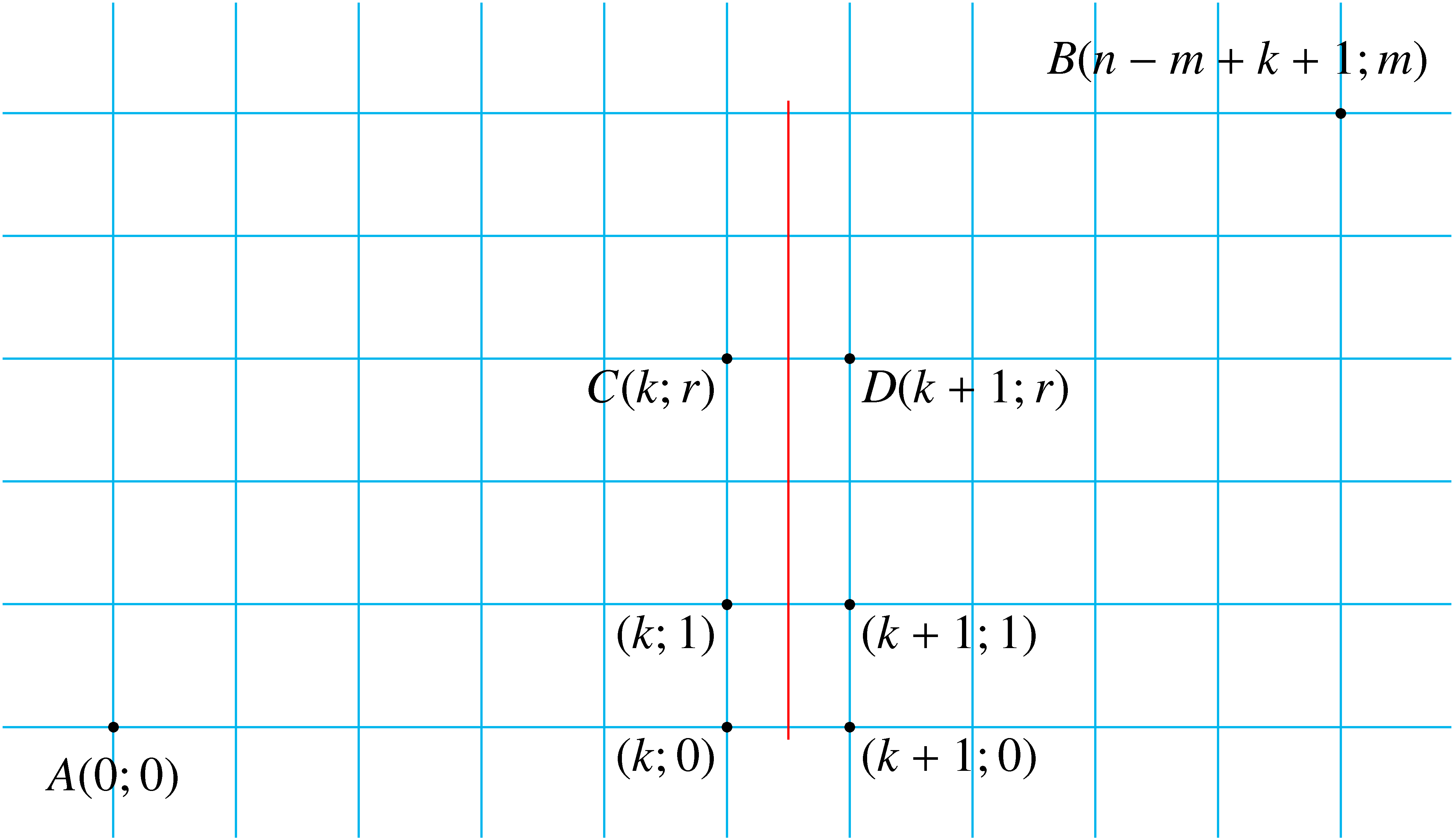
A másik fajta összeszámlálás: osztályozzuk az utakat aszerint, hogy hol lépik át az ábrán pirossal behúzott egyenest (minden út pontosan egyszer teszi ezt). A 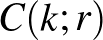 pontból a
pontból a 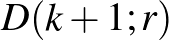 pontba lépve (
pontba lépve (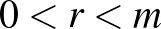 ) az összes itt átvezető utak száma az
) az összes itt átvezető utak száma az 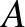 -ból a
-ból a  -be, és a
-be, és a 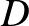 -ből a
-ből a 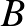 -be vezető utak számának szorzata:
-be vezető utak számának szorzata: 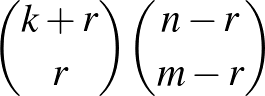 . Ezek összege (ami a bizonyítandó összefüggés bal oldala) adja az összes út számát.
. Ezek összege (ami a bizonyítandó összefüggés bal oldala) adja az összes út számát.
(c) Az előbbihez hasonló módon számolhatunk. Most az 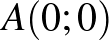 pontból a
pontból a 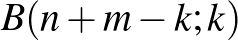 pontba vezető utakat számoljuk össze. Az alábbi ábrán pirossal jelölt egyenest is minden út egyszer metszi (valamelyik rácspontban). Ennek a piros egyenesnek a rácspontjaiba
pontba vezető utakat számoljuk össze. Az alábbi ábrán pirossal jelölt egyenest is minden út egyszer metszi (valamelyik rácspontban). Ennek a piros egyenesnek a rácspontjaiba 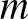 lépésben jutunk el. Az
lépésben jutunk el. Az 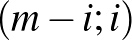 pontba
pontba 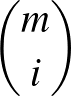 , innen tovább
, innen tovább 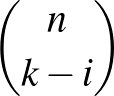 -féleképpen haladhatunk, ahol
-féleképpen haladhatunk, ahol 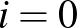 , 1, 2, ...,
, 1, 2, ..., 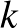 . Az ilyen szorzatok összege az utak száma, azaz
. Az ilyen szorzatok összege az utak száma, azaz 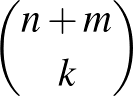 .
.
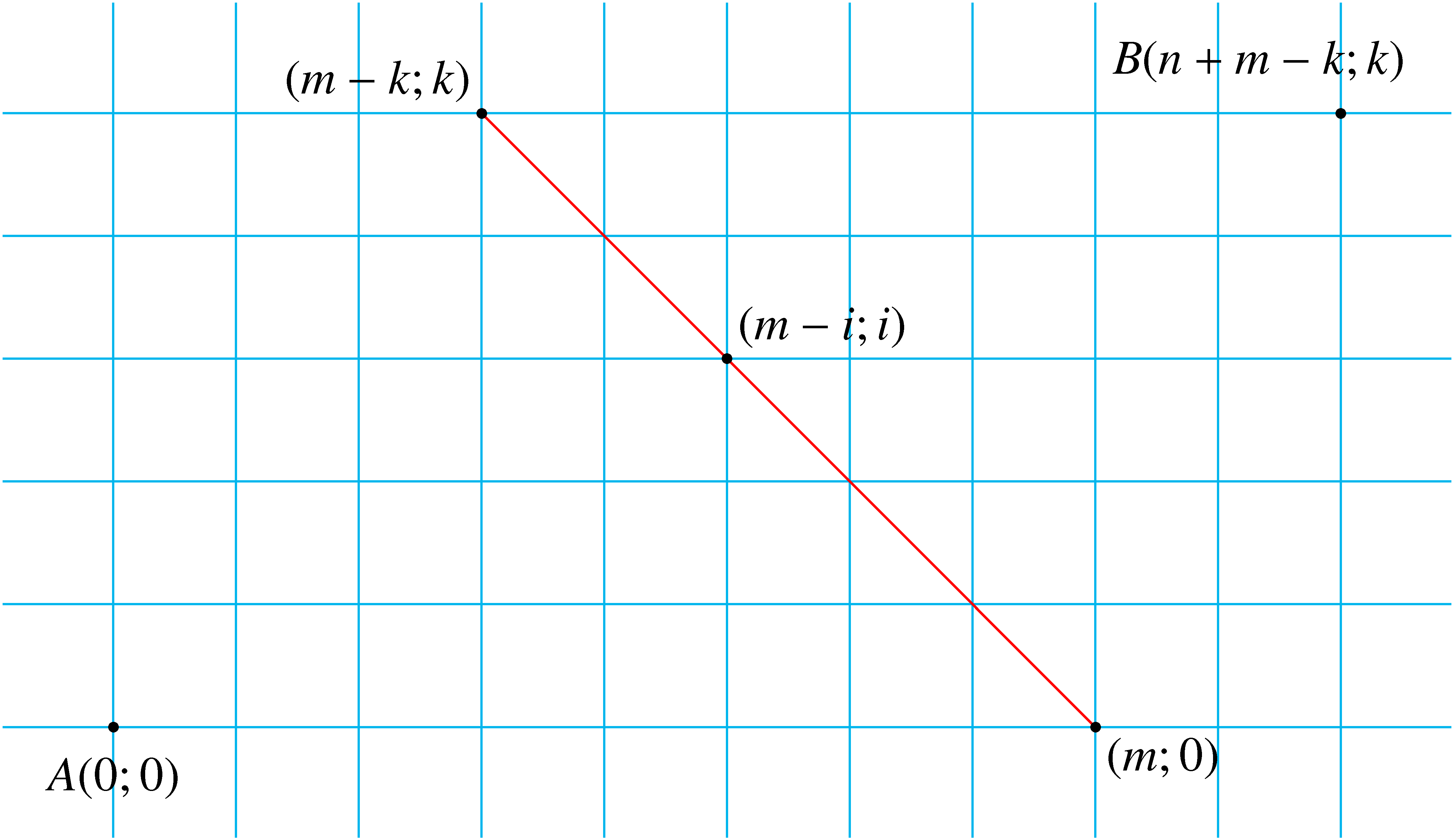
Megjegyzés. A (b) és a (c) részek szép példát mutatnak a kettős leszámlálás módszerére.
10. Hány egész számpár megoldása van az 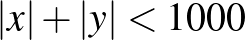 egyenlőtlenségnek?
egyenlőtlenségnek?
Megoldás. Az alábbi ábrák kétféle összeszámlálást szemléltetnek:
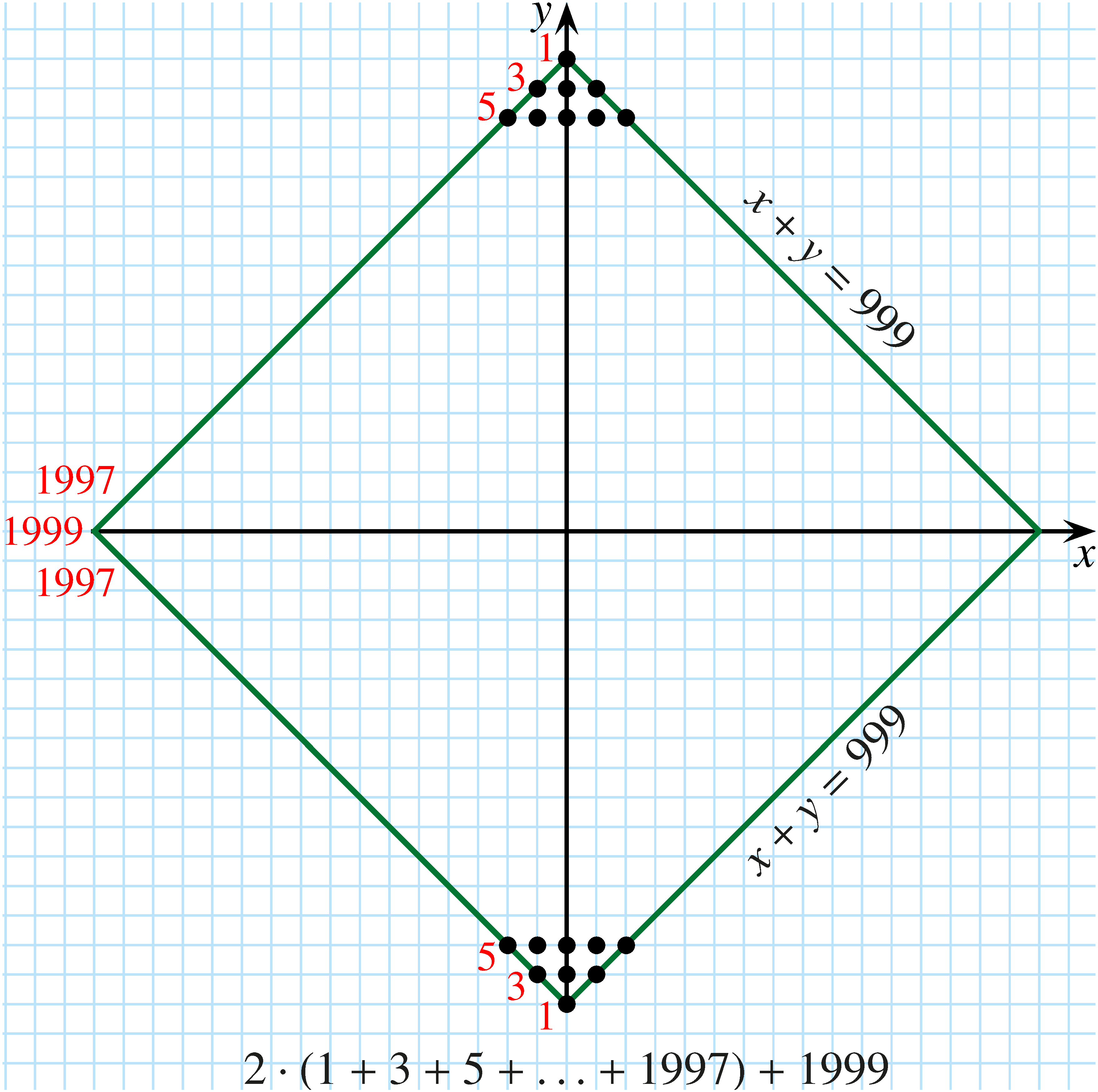
A koordináta-rendszerben ábrázolva a ponthalmazt, egy négyzet rácspontjait kell összeszámlálnunk. Az egyik ábra „vízszintes” összeszámlálást sugall a 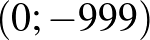 pontból kiindulva a vízszintes rácsegyeneseken felfelé haladva egészen a
pontból kiindulva a vízszintes rácsegyeneseken felfelé haladva egészen a 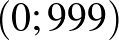 pontig. Ez, a szimmetriát kihasználva, az ábrán látható összeget eredményezi:
pontig. Ez, a szimmetriát kihasználva, az ábrán látható összeget eredményezi:
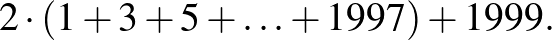
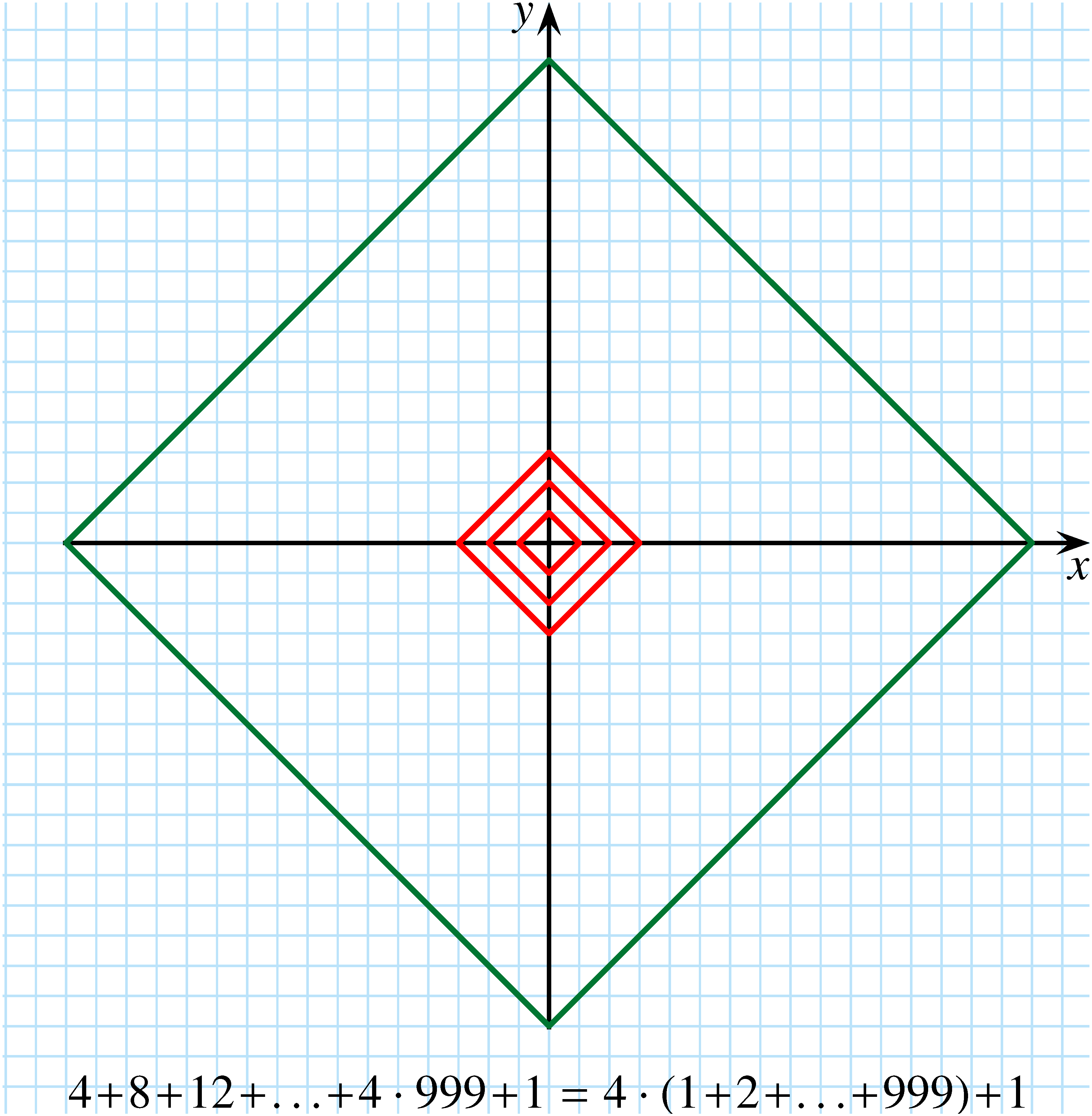
A másik ábra az origó középpontú hasonló négyzetek kerületi pontjait számolja össze, amelyek egy 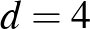 differenciájú számtani sorozat első 999 összegét eredményezik, amelyhez egyet hozzáadva (ez az origó) kapjuk az eredményt:
differenciájú számtani sorozat első 999 összegét eredményezik, amelyhez egyet hozzáadva (ez az origó) kapjuk az eredményt:
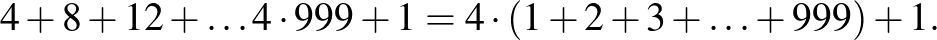
Az összeg mindkét esetben 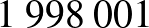 .
.
11. Melyek azok a pozitív egész számok, amelyek nem írhatók fel több egymást követő természetes szám összegeként?
Megoldás. Szomszédos pozitív egész számok összegét szemléltethetjük egy olyan „vízszintes” rácstrapéz segítségével, mint ami például az ábra bal oldalán látható. A trapéz alapjainak hossza az összeadandó számok legkisebbike, illetve legnagyobbika, valamint az alapokkal párhuzamos, egymást követő rácsszakaszok hossza éppen a szóban forgó számokkal egyezik meg. Itt most szakasz hossza alatt a szakaszon lévő rácspontok számát értjük. (Az ábrán látható bal oldali trapéz például a 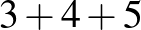 összeget szemlélteti.) Ha egy ilyen rácstrapézt egy vele egybevágó trapézzal összeillesztünk az ábrán látható módon (az
összeget szemlélteti.) Ha egy ilyen rácstrapézt egy vele egybevágó trapézzal összeillesztünk az ábrán látható módon (az 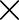 -szel jelölt pontra tükrözve), akkor egy olyan rácstéglalaphoz jutunk, amelyben a rácspontok száma kétszerese az alapul vett trapéz rácspontjai számának.
-szel jelölt pontra tükrözve), akkor egy olyan rácstéglalaphoz jutunk, amelyben a rácspontok száma kétszerese az alapul vett trapéz rácspontjai számának.
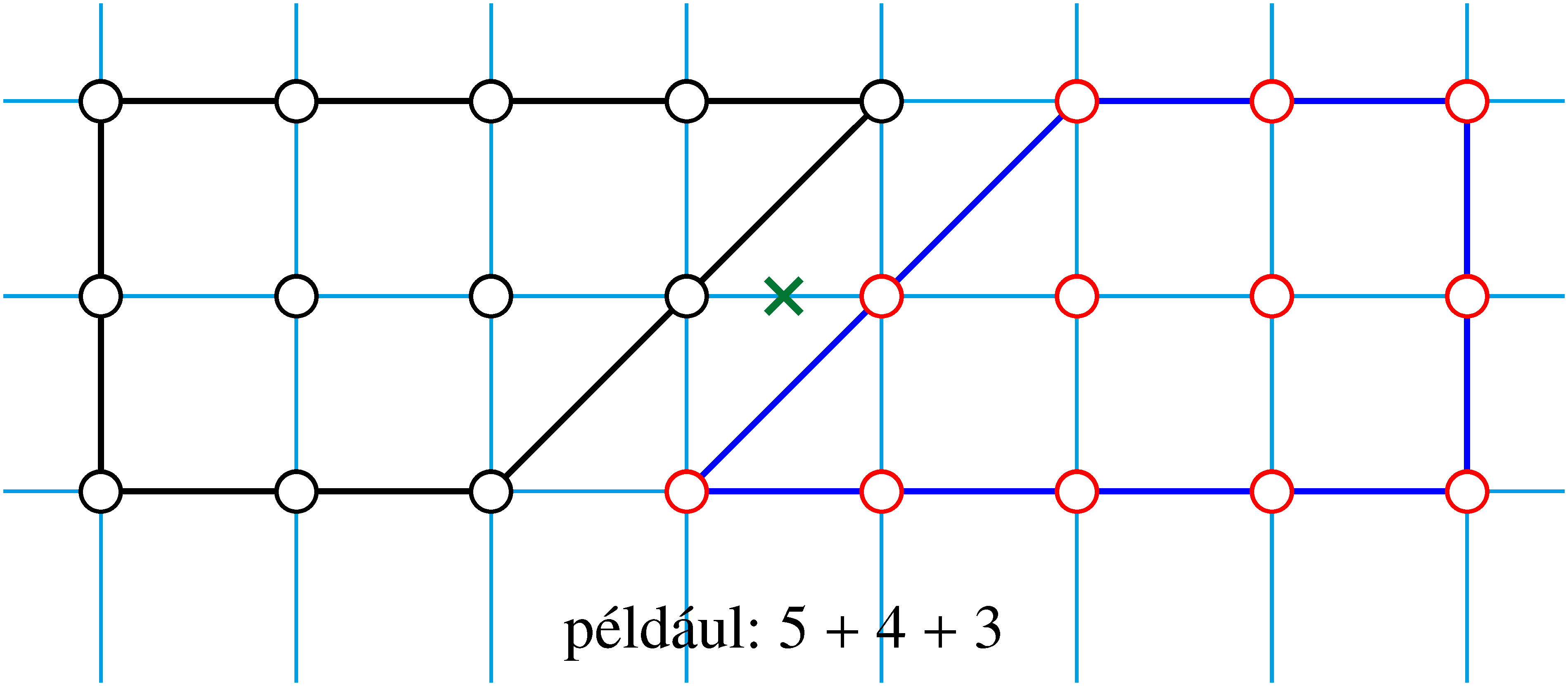
Világos, hogy egy 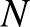 pozitív egész szám pontosan akkor állítható elő szomszédos pozitív egészek összegeként, ha található hozzá a fenti módon megfelelő rácstrapéz. Ez pedig ekvivalens azzal, hogy egy
pozitív egész szám pontosan akkor állítható elő szomszédos pozitív egészek összegeként, ha található hozzá a fenti módon megfelelő rácstrapéz. Ez pedig ekvivalens azzal, hogy egy 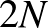 rácspontot tartalmazó rácstéglalap szimmetriacentrumán áthaladó
rácspontot tartalmazó rácstéglalap szimmetriacentrumán áthaladó 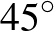 -os egyenes a téglalapnak nem tartalmazza egyetlen rácspontját sem Ez csakis páratlan
-os egyenes a téglalapnak nem tartalmazza egyetlen rácspontját sem Ez csakis páratlan 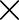 páros típusú rácstéglalapok esetén teljesül (amint az a következő három ábráról látható). Ez azt jelenti, hogy
páros típusú rácstéglalapok esetén teljesül (amint az a következő három ábráról látható). Ez azt jelenti, hogy 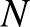 -nek lennie kell páratlan osztójának.
-nek lennie kell páratlan osztójának.
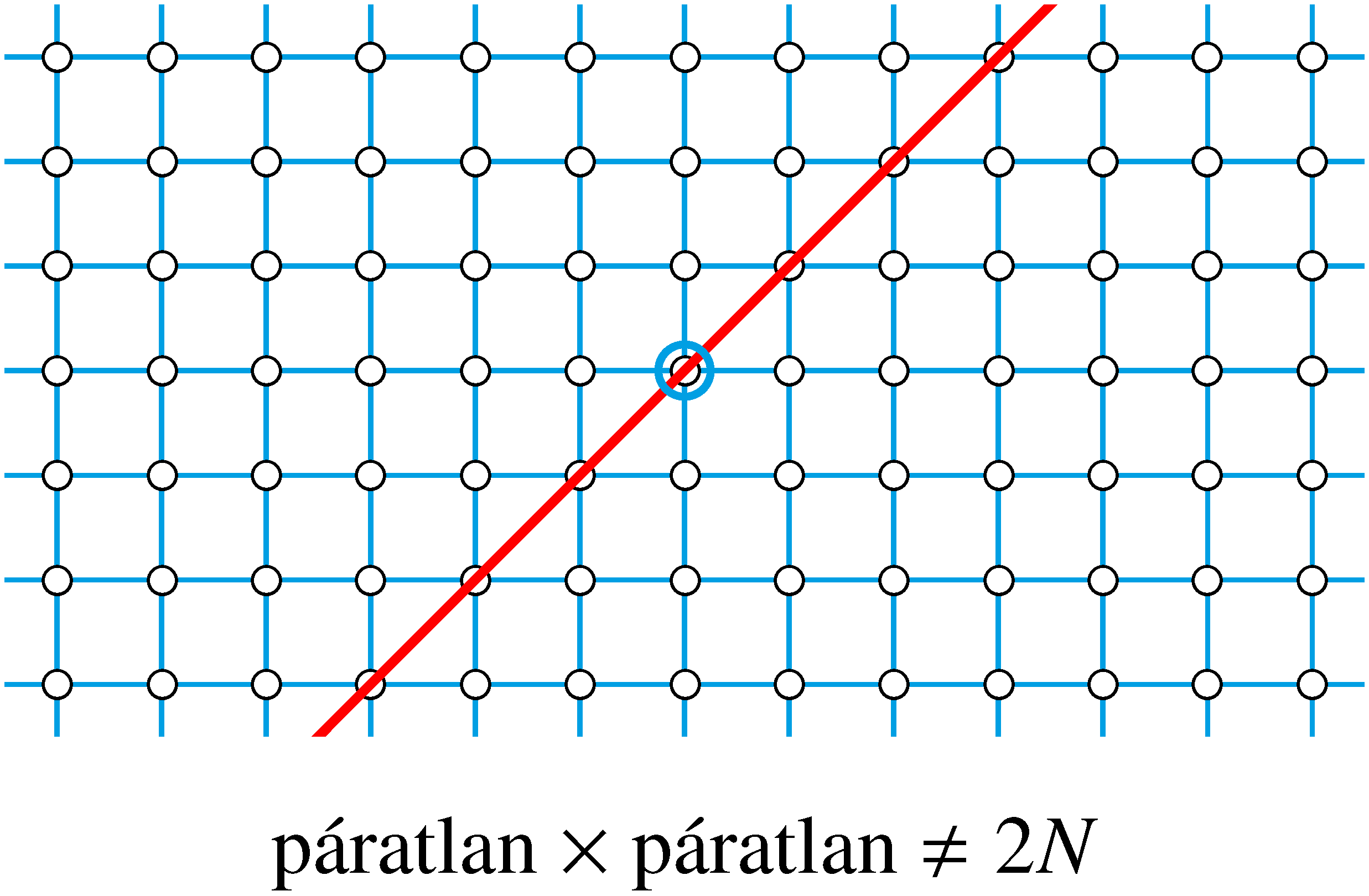
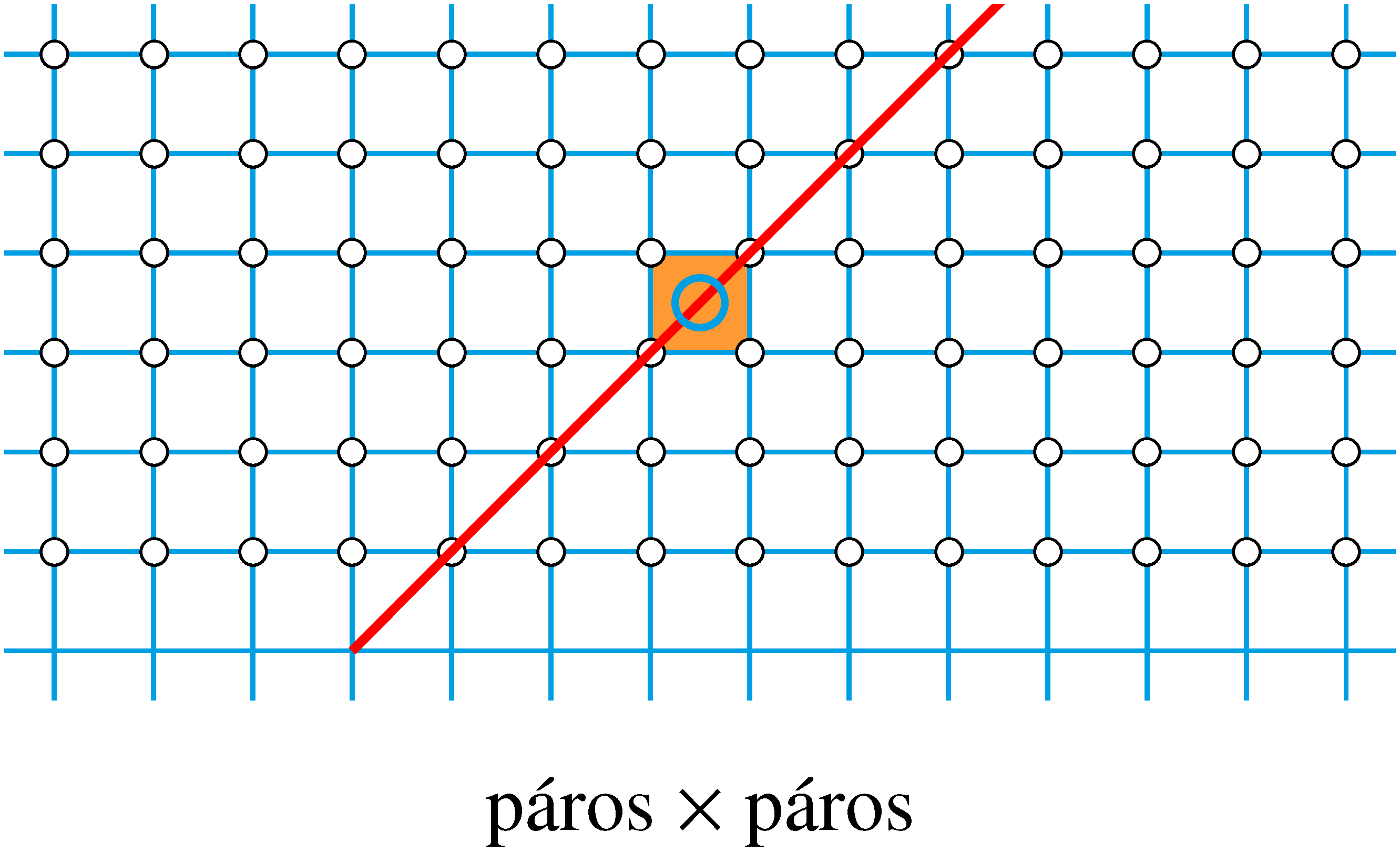
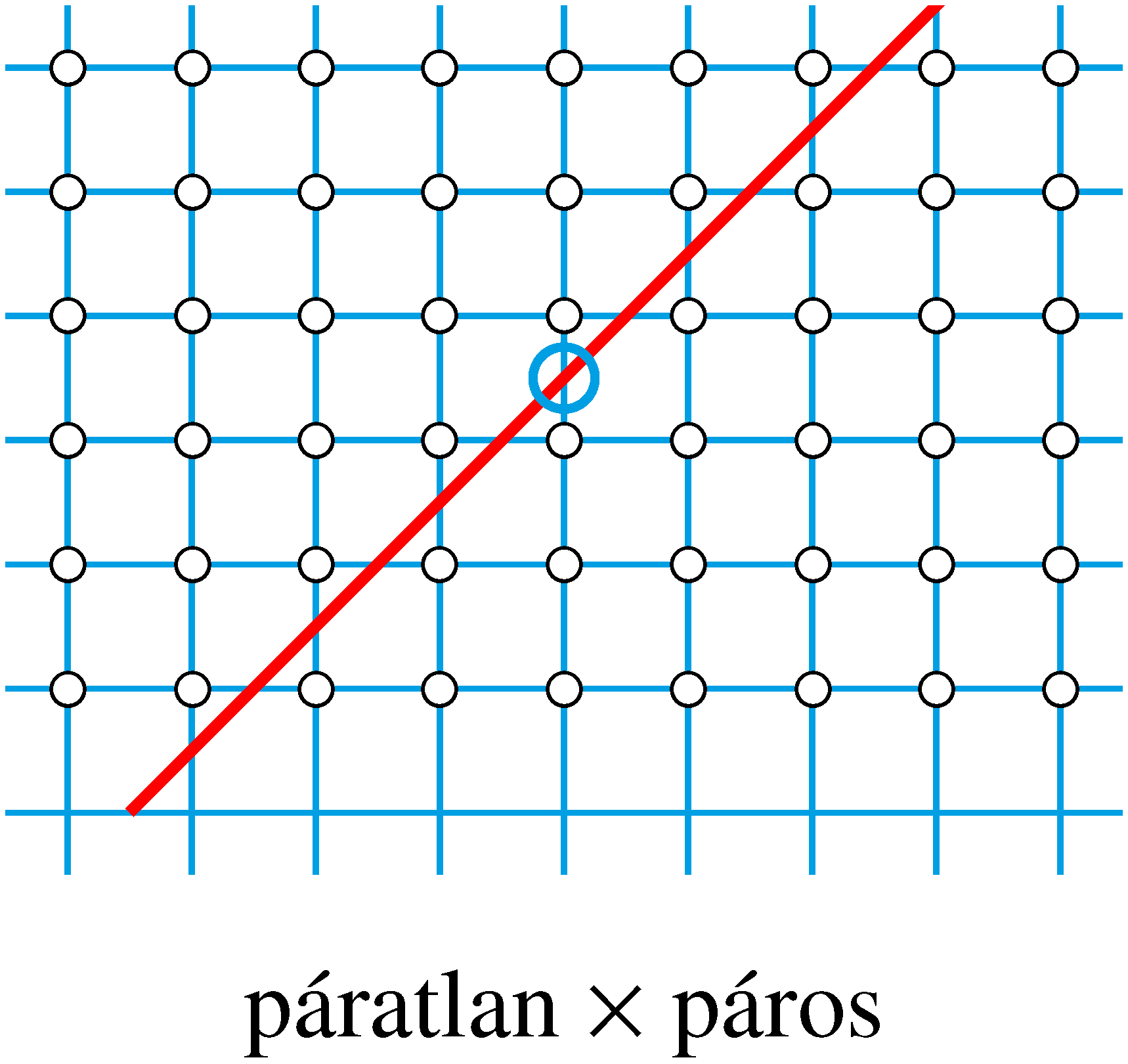
Azt kaptuk tehát, hogy egy 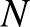 pozitív egész szám pontosan akkor nem állítható elő szomszédos egész számok összegeként, ha
pozitív egész szám pontosan akkor nem állítható elő szomszédos egész számok összegeként, ha 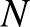 -nek nincs páratlan osztója, következésképpen ha a szám 2-hatvány.
-nek nincs páratlan osztója, következésképpen ha a szám 2-hatvány.
12. Egy könyvtár be- és kijáratánál egy-egy tábla áll. Minden be-, illetve kilépőnek fel kell írnia a megfelelő táblára, hogy hány embert talált bent, illetve hagyott ott a könyvtárban. Bizonyítsuk be, hogy egy teljes nap során ugyanazok a számok kerülnek a két táblára, legfeljebb más sorrendben (feltesszük, hogy egyszerre csak egy ember érkezik, vagy távozik).
Megoldás.
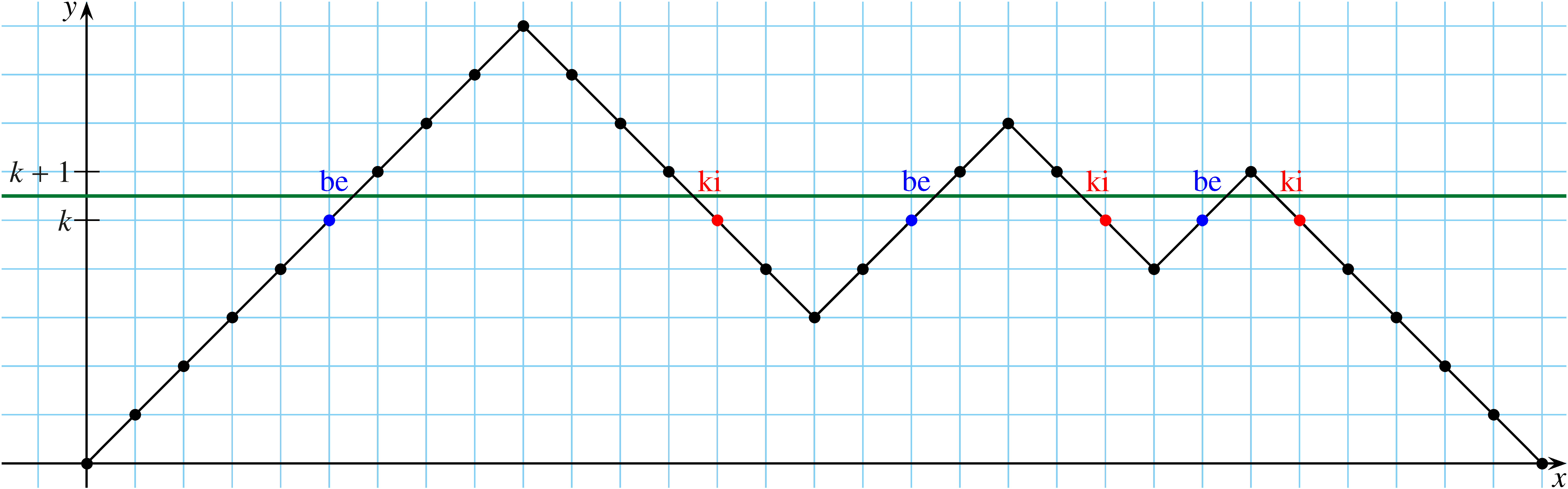
A koordináta-rendszerben egy pont 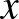 koordinátája jelölje azt, hogy hányadszorra változott a létszám,
koordinátája jelölje azt, hogy hányadszorra változott a létszám, 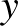 koordinátája pedig az éppen jelen lévő személyek számát. Az ezeket összekötő töröttvonal az
koordinátája pedig az éppen jelen lévő személyek számát. Az ezeket összekötő töröttvonal az 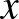 tengellyel egy vagy több zárt sokszöget alkot. Nézzük meg, hogy egy
tengellyel egy vagy több zárt sokszöget alkot. Nézzük meg, hogy egy 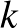 szám hányszor kerül felírásra a bejáratnál, és hányszor a kijáratnál! Egy, az
szám hányszor kerül felírásra a bejáratnál, és hányszor a kijáratnál! Egy, az 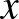 tengellyel párhuzamos egyenes a
tengellyel párhuzamos egyenes a 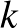 és
és 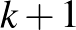 szám között ugyanannyiszor lép be a sokszög(ek)be, ahányszor kilép belőle (belőlük). Tehát egyforma számú emelkedő és süllyedő szakaszt metsz át. Minden emelkedéskor a
szám között ugyanannyiszor lép be a sokszög(ek)be, ahányszor kilép belőle (belőlük). Tehát egyforma számú emelkedő és süllyedő szakaszt metsz át. Minden emelkedéskor a 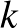 szám kerül a bejárati táblára, minden süllyedéskor pedig a kijárati táblára. Ezzel állításunkat bizonyítottuk.
szám kerül a bejárati táblára, minden süllyedéskor pedig a kijárati táblára. Ezzel állításunkat bizonyítottuk.
13. Egy jegypénztárnál nyolcan állnak sorba. Négyüknél egy-egy ezerforintos, a másik négynél egy-egy kétezerforintos van, a sorrendjük ismeretlen. A jegy ára 1000 Ft, a kassza kezdetben üres. Mindenki egy jegyet szeretne vásárolni. Hány olyan sorrend van, amikor a pénztáros fennakadás nélkül ki tudja adni a jegyet? (Általánosítsunk 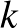 darab 1000-es,
darab 1000-es, 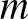 darab 2000-esre!)
darab 2000-esre!)
Megoldás. Jelölje adott sorban E az ezrest, K a kétezrest. Egy „jó” sorozat pl. a következő: EKEEKEK. Milyen is egy jó sorozat? Az, amelyet bárhol elvágva, az E-k száma nem kisebb a K-k számánál. Ha tekintünk egy sakktáblát, amelynek bal alsó sarkából indulva E esetén jobbra, K esetén felfelé lépünk, akkor éppen azok a jó utak, amelyek a 6. feladatban, és a megoldás szó szerint megismételhető.
Fejér Szabolcs,
a miskolci Földes Ferenc Gimnázium nyugdíjazott tanára
Hivatkozások
- [1] KÖMAL, OKTV, Kürschák versenyek és a Nemzetközi Magyar Matematikai versenyek példái
[2] Hajnal Péter: Elemi kombinatorikai feladatok (Polygon 1997.)
[3] Hajnal Péter: Összeszámlálási problémák (Polygon 1997.)
[4] Reiman István: A geometria és határterületei (Gondolat 1986.)
[5] A. M. Jaglom – I. M. Jaglom: Nem elemi feladatok elemi tárgyalásban (Typotex 2015.)











