Egy Schweitzer-feladat megoldása középiskolás eszközökkel – 2. rész

2024. júniusában jelent meg az Egy Schweitzer-feladat megoldása középiskolás eszközökkel. Ennek bevezetőjét érdemes elolvasni, mielőtt rátérnénk a mostani cikk nem kevésbé érdekes feladatának megoldására. A júniusi számban megjelent cikk folytatásaként ismét egy első látásra ijesztő, de középiskolások számára is érthető Schweitzer-feladat megoldását fogjuk taglalni. Az előző részben részletesen beszámoltam a verseny múltjáról és jellegzetességeiről. Bár a feladat megfogalmazásából az sejlik, hogy kőkemény egyetemi szintű tudásra lesz szükség a megoldásához, ez korántsincs így: a mátrix megnevezés félrevezető ebben a helyzetben, a probléma semmiféle tudást nem igényel a mátrixok elméletéből. A bizonyítás tisztán kombinatorikai, és elegendő mátrixok helyett táblázatokra gondolni, amelyeknek minden cellájába 0 vagy 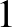van írva. Lássuk is a példát!

Feladat. (Schweitzer, 2018/3.) Egy 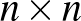-es mátrixot jólfésültnek hívunk, ha minden eleme 0 vagy 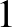, és nem tartalmazza az 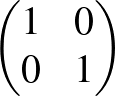mátrixot részmátrixként. Lássuk be, hogy van olyan konstans, amelyre teljesül, hogy bármely 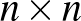-es jólfésült mátrixnak van olyan, legalább 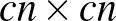-es részmátrixa, melynek minden eleme egyforma. (Egy jólfésült mátrix tartalmazhatja a 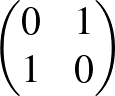mátrixot részmátrixként.)

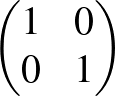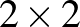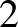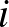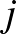Megoldás. Először tisztázzuk, mit is jelent pontosan az, hogy a mátrix nem tartalmazza az mátrixot részmátrixként. Részmátrixnak nem csak a folytonos -es résztáblázatokat nevezzük, hanem bármely cellát, amelyet úgy kapunk, hogy az eredeti mátrixnak kiválasztjuk sorát (. és .) és 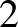oszlopát (. és 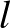.), és tekintjük ezeknek mind a 4 metszetében lévő cellákat.

Mindezek tudatában vágjunk bele a megoldásba!

A bizonyítás a következő intuíción alapszik: ha van egy olyan sor a táblázatban, amiben „sok” (ami itt azt jelenti, hogy 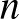valamilyen konstansszorosa) 1-es van, és ezeket ezután még „sok” 0 követi, továbbá még elegendően „sok” sor található ezen sor alatt, akkor a jólfésültségi feltételt kihasználva könnyen találhatunk egy csupa azonos elemből álló részmátrixot. Ugyanis, ha ekkor egy lejjebb lévő sorban bármelyik 1-es alatt 0 van, akkor a jólfésültségi feltétel miatt muszáj minden őt követő 0 alatt 0-nak állnia, különben találnánk egy tiltott részmátrixot, vagyis abban a lentebbi sorban is „sok” 0 lenne. Ha pedig nincs ilyen 1-es, akkor az eredeti sorunk minden 1-ese alatt 1-esnek kell állnia a lentebbi sorban.

Tehát a kiválasztott sorunk alatti minden sorra igaz, hogy vagy az eredeti sor minden 1-ese alatt 1-es van, vagy az eredeti sor minden 0-ja alatt 0 van. Ha elég „sok” sor van a sorunk alatt, akkor valamelyik eset „sokszor” fog fennállni (hiszen a lentebbi sorok legalább felére ugyanaz az eset fog vonatkozni), és ezen sorokat és a hozzá tartozó megfelelő oszlopokat kiválasztva találni fogunk egy megfelelő 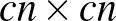-es csupa azonos elemből álló részmátrixot valamilyen konstansra.

Kicsit továbbgondolva a fenti gondolatmenetet, azt is láthatjuk, hogy az is jó nekünk, ha olyan sort találunk, amelyben „sok” 0-t követ sok 1-es, csak ekkor kellően „sok” sornak kell a sorunk fölött lennie (ellentétben az előző esettel, ahol kellően „sok” sor kellett alatta), és ekkor gyakorlatilag működik ugyanaz a gondolatmenet, mint az előbb.

Ugyanakkor, ha egy sorban kellően „sok” 0 és kellően „sok” 1-es van egyszerre, akkor mindig lesz olyan szituáció, amikor „sok” 0 vagy 1 megelőzi a másik karaktert, hiszen csak megnézzük, melyikből gyűlik össze legalább a fele a konstansunknak, és utána a másiknak még mindig hátra lesz legalább a fele. Ha a mátrix közepéről indulunk ki, azt is tudjuk biztosítani, hogy amennyiben találunk egy ilyen sort, akkor alatta és felette is kellően „sok” sor legyen. Mivel a jólfésült mátrix részmátrixa is jólfésült, nekünk az teljesen megfelelő, ha a középső harmadon belül találunk megfelelő részmátrixot. Hiszen ha ehhez a középső részmátrixhoz találunk jó 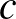konstanssal csupa azonos elemből álló részmátrixot, akkor az az eredeti mátrixhoz is jó lesz (körülbelül konstanssal).

Most írjuk le mindezt matematikailag precízen!

Jelöljük a mátrixunkat -val. Feltehetjük, hogy ( esetén választhatunk egy 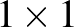-es részmátrixot, ami triviálisan csak azonos elemekből fog állni, és ez megfelelő lesz minden 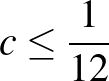pozitív konstansra, és a mi végső konstansunk kisebb lesz ennél). Ekkor fel tudjuk osztani az eredeti táblázatot 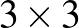darab résztáblázatra az ábrán látható módon úgy, hogy mind a 9 résztáblázatnak legalább 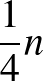darab sora és legalább 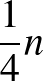darab oszlopa legyen (a sorokat és oszlopokat fel tudjuk 3-3 részre osztani úgy, hogy minden részben legalább sor/oszlop van, és mivel , ezért ). 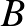Nevezzük a felosztott mátrix középső mátrixát -nek!

Tegyük fel, hogy létezik 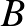-nek olyan sora, amiben legalább darab 0 és legalább darab 1 van (a bizonyítás későbbi részéből kiderül, miért választottuk pont az 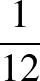-et itt konstansnak), legyen ez a sor az 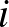. sor. Menjünk végig balról jobbra ezen sor elemein 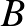-n belül, és figyeljük, hogy melyikből gyűlik össze először legalább 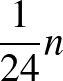darab!

(a) Tegyük fel először, hogy az 1-es gyűlik össze hamarabb (0-ból vagy 1-ből), és jelölje az első 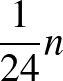darab egyeshez tartozó oszlopok halmazát 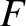. Ekkor miután összegyűlt 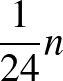darab 1-es, még utána kell lennie tőlük jobbra 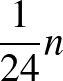darab 0-nak (hiszen az 1-eseinkig még nem gyűlt össze belőlük 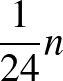darab sem, és összesen legalább van a 0-kból, úgyhogy legalább még 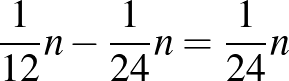darab hátra van), jelölje ezen 0-k oszlopainak halmazát .

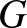Tekintsük a 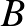alatti részmátrixot az 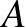felosztásában, ennek legalább 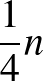sora van a konstrukciónk szerint. Ha ezen sorok bármelyikében az 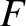-ben lévő oszlopok bármelyikének helyén 0 áll, akkor a 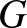-hez tartozó oszlopokban ezen soron belül mindenhol 0-nak kell lennie, mert ellenkező esetben találnánk egy 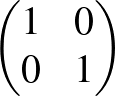részmátrixot, kiválasztva az 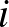. sort és ezt a sort, valamint azt az oszlopot 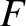-ből, amelynél a jelenlegi sorban 0 áll, és azt az oszlopot 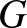-ből aminél a jelenlegi sorban 1 áll.

Ez azt jelenti, hogy a 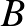alatti részmátrix minden sora kétféleképpen nézhet ki: vagy az 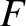-ben lévő oszlopok mindegyikének helyén 1 áll, vagy a 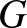-ben lévő oszlopok mindegyikének helyén 0 áll. Mivel ennek az alsó részmátrixnak legalább 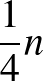sora van, valamelyik lehetőség legalább 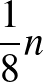sor esetén fennáll. Mivel 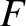-ben és 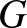-ben is legalább 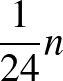darab oszlop van, ezért mindkét esetben kiválasztható lesz vagy egy 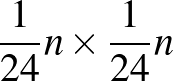-es csupa 1 vagy csupa 0 mátrix, és ezzel ebben az esetben beláttuk a feladat állítását 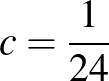-re.

(b) Ha először a 0-ból gyűlik össze 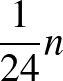darab a 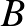sorában, akkor az előbbi gondolatmenetet lemásolva szintén tudunk egy legalább 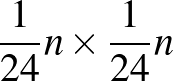-es csupa 1 vagy csupa 0 részmátrixot találni, csak ebben az esetben nem a 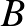alatti, hanem a 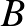feletti részmátrixot kell tekintenünk.

Még ennél is többet ki lehet hozni az előző módszerből: ha -nek van olyan oszlopa, amelyben legalább darab 0 és legalább darab 1 van, akkor analóg módon használva az előző bizonyítást, tudunk találni legalább 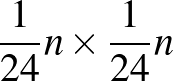-es csupa 1 vagy csupa 0 részmátrixot, csak ebben az esetben nem a alatti és feletti, hanem a -től jobbra, illetve -től balra található részmátrixot kell vizsgálnunk.

Tehát, ha -nek van olyan sora vagy olyan oszlopa, amelyben legalább darab 0 és legalább darab 1 van, akkor készen vagyunk. Feltehetjük tehát, hogy -ben nincs sem ilyen sor, sem ilyen oszlop, ami viszont azt jelenti, hogy -nek minden sorában és minden oszlopában vagy legalább darab 0, vagy legalább 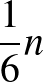darab 1 van.

Mivel 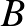-nek legalább 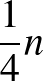sora van, ezért találhatunk vagy legalább 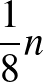sort, amelyben legalább 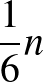darab 0 van, vagy legalább 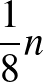sort, amelyben legalább 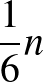darab 1 van (vagyis, kellően sok sorban az egyik elemből nagyon sok van).

(a) Tegyük fel először, hogy a 0-s eset áll fenn, és válasszuk ki ezt a legalább 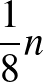darab sort 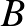-ből, így kapjuk a 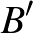részmátrixot. 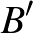-ben legalább 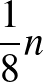darab sor van, mindegyikben legalább 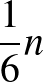darab 0, ezért 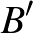-ben minimum 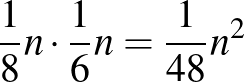darab 0 elemnek kell lennie. De így az is igaz, hogy van 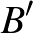-ben legalább 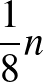oszlop is úgy, hogy mindegyikben legalább 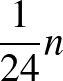darab 0 van, hiszen ellenkező esetben 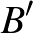-n belül kevesebb, mint 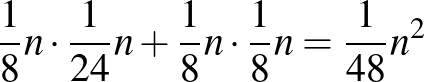darab 0 lenne, ami ellentmondás.

Válasszuk ki 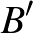-ből ezt a legalább 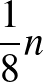darab oszlopot, így kapjuk a 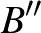mátrixot. A konstrukcióból adódik, hogy 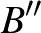minden oszlopában legalább 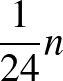darab 0 van, de az is igaz, hogy minden sorában is legalább 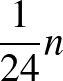darab 0 van, hiszen 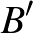minden sorában legalább 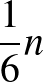darab 0 van, és mindegyikből legfeljebb 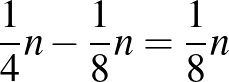darabot vettünk el, amikor kiválasztottuk oszlopait (és ).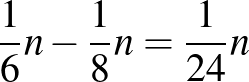

Tehát 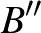minden sorában és minden oszlopában is legalább 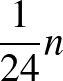darab 0 van. Most megint nagyon hasonló módon fogunk eljárni, mint a bizonyítás első részében: vegyük a mátrix bal felső negyedét, ami egy 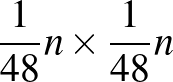-es mátrix. Ha ebben csak 0 van, akkor készen vagyunk ( 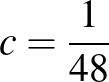-dal), ellenkező esetben pedig van egy 1-es ebben a bal felső sarokban. De ennek az 1-esnek a sorában tőle jobbra található még legalább 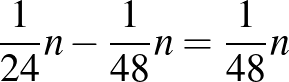darab 0 (hiszen a sorban legalább 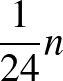darab 0 van, és ebből a bal felső sarkunk legfeljebb 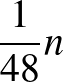darabot tartalmazhat), és ugyanúgy az is igaz, hogy ezen 1-esnek az oszlopában, alatta még található legalább 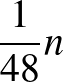darab 0. De ekkor a jólfésültség miatt ezen 0-k sorainak és oszlopainak metszetében csak 0 állhat, így ekkor találtunk egy 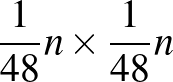-es csupa 0 részmátrixot.

(b) Ha 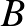-ben van legalább 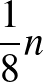sor, amiben legalább 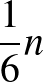darab 1 van, akkor a bizonyítás pontosan ugyanúgy megy, mint az előbb, azzal a különbséggel, hogy ekkor 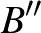-nek nem a bal felső 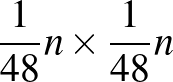-es sarkát, hanem a jobb alsó 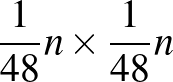-es sarkát kell tekintenünk, és ebből fogunk találni egy legalább 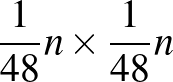-es csupa 1 részmátrixot. 

 Szőke Tamás